Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

132 Integration: Applications

(b) Write the integral that gives the Cartesian components of the electric ﬁeld

at an arbitrary point (x, y, z) in space.

multiple of k

λ/a.

4.17. Consider a uniform linear charge distribution, with linear charge density

λ, in the form of an elliptical helix whose parametric equation is given by



= a cos t, y



= b sin t, z



= ct

Use Cartesian coordinates.

(a) Write down the integrals that give the electric ﬁeld and the electric po-

tential at an arbitrary point P in space.

(b)Verifythatwhenc = 0, you get the ﬁeld and potential of an ellipse (see

Problem 4.15).

line segment.

(d)Verifythatwhenc =0=b and a →∞, you get the ﬁeld of an inﬁnite

straight line.

4.18. Find the three components of the electric ﬁeld and the potential of Ex-

ample 4.1.2 when a = −L/2andb = L/2. Approximate the three components

of the electric ﬁeld for the case where L>>x.

4.19. Derive all relations in Equations (4.20) and (4.21).

4.20. Figure 4.18 shows a hyperbola y =

√

+ a

. Only the segment be-

tween x =0andx = a is charged uniformly with linear density λ.

(a) Write the expression for E as an integral in Cartesian coordinates.

(b) Find the three components of E as integrals over x



= au, write each component as a numerical

multiple of k

λ/a.

4.21. A circular ring of radius a is uniformly charged with linear density λ.

The ring rotates with angular speed ω about the axis perpendicular to the

plane of the ring, passing through its center.

Figure 4.18: The segment of the hypebola that is charged.

4.4 Problems 133

(a) Find an expression for each of the three components of the magnetic

ﬁeld at an arbitrary point in space in terms of an integral in an appropriate

coordinate system. Evaluate the integrals whenever possible.

(b) Find the components of the ﬁeld at the point P showninFigure4.17.

Express your answers as a numerical multiple of k

λω. (You will need to

evaluate some integrals numerically!)

4.22. An elliptical conducting ring of semi-major axis a and semi-minor axis

b carries a current I.

(a) Find an expression for each of the three Cartesian components of the

magnetic ﬁeld at an arbitrary point in space in terms of an integral in the

Cartesian coordinate system.

(b) Find an integral expression for the components of the ﬁeld at a point on

the line perpendicular to the ellipse that passes through its center.

4.23. Perform the integrals for E

, E

,andE

of Example 4.2.1 when the

ﬁeld point is on the z-axis. Hint: You can get E

and E

without doing the

integrals.

4.24. Assume that the parametric equations of a current loop are x



f(t),y



= g(t),z



= h(t). By writing everything in Equation (4.18) in Carte-

sian coordinates, show that

(r)=k



(t)

z − h(t)

− h



(t)

y − g(t)

x − f(t)

y − g(t)

z − h(t)

3/2

dt,

(r)=k



(t)

x − f(t)

− f



(t)

z − h(t)

x − f(t)

y − g(t)

z − h(t)

3/2

dt,

(r)=k



(t)

y − g(t)

− g



(t)

x − f(t)

y − g(t)

z − h(t)

3/2

dt,

where a and b are the initial and ﬁnal values of the parameter t.

4.25. By writing everything in Equation (4.18) in cylindrical coordinates,

show that

= k

dρ



+ ρ



dϕ



+ ρ



sin(ϕ



− ϕ) dz



+ ρ

2

− 2ρρ



cos(ϕ − ϕ



)+(z − z



)

3/2

= k



dϕ



− N

dρ



ρ −ρ



cos(ϕ



− ϕ)



+ ρ

2

− 2ρρ



cos(ϕ − ϕ



)+(z − z



)

3/2

= −k

ρ sin(ϕ



− ϕ) dρ



ρρ



cos(ϕ



− ϕ) − ρ

2

dϕ



+ ρ

2

− 2ρρ



cos(ϕ − ϕ



)+(z − z



)

3/2

where

≡ (z − z



)sin(ϕ



− ϕ),N

≡ (z − z



)cos(ϕ



− ϕ)

134 Integration: Applications

Figure 4.19: The ﬁgure for Problem 4.28.

4.26. Derive Equation (4.27).

4.27. Derive Equation (4.29) from Equation (4.28).

4.28. Asquareofside2a is uniformly charged with surface density σ.

(a) Find the electrostatic potential at an arbitrary point in space. Do one

of the integrals and express your answer in terms of a single integral in an

appropriate coordinate system.

(b) Find the potential at a point a distance a directly above the midpoint of

one of the sides as shown in Figure 4.19. Express your answer as a numerical

multiple of k

σa.

4.29. The area in the xy-plane shown in Figure 4.21 is uniformly charged

with surface charge density σ. The equation of the parabolic boundary is

y = x

/a. Assume that the observation point (ﬁeld point) P is on the z-axis

at z = a.

(a) Derive the Cartesian components of the electric ﬁeld at P as double inte-

grals.

(b) Do the y



integration ﬁrst and then the x



integration to ﬁnd the compo-

nents of the electric ﬁeld. Write your answers as a numerical multiples of k

σ.

You will need to evaluate certain integral(s) numerically.

4.30. Using cylindrical coordinates, ﬁnd the electrostatic ﬁeld of a uniformly

charged circular disk of charge density σ and radius a:

(a) at an arbitrary point in space;

(b) at an arbitrary point on the perpendicular axis of the disk; and

Figure 4.20: The region of the xy-plane that is charged.

4.4 Problems 135

−

Figure 4.21: The shaded region is uniformly charged.

(d) For (b), consider the case of inﬁnite radius and compare your result with

the inﬁnite rectangle discussed in introductory physics books and Example

4.2.3.

4.31. Figure 4.20 shows a region of the xy-plane that is uniformly charged

with surface charge density σ.Theboundary of the region is given in a

polar/cylindrical coordinate system by ρ = a cos(2ϕ)with−π/4 ≤ ϕ ≤ π/4.

We are interested in the electrostatic potential at a point P on the z-axis with

z = a.

(a) Write the position vector of P and P



(a typical source point) in cylindrical

coordinates. Now evaluate |r − r



(b) Write the expression for dq(r



) in cylindrical coordinates.

coordinates.

(d) Perform one of the integrations, and wrtie your ﬁnal answer as a single

integral.

(e) Find the value of the potential as a numerical multiple of k

σa.

4.32. A cylindrical shell of radius a and length L is uniformly charged with

surface charge density σ. Using an appropriate coordinate system and axis

orientation:

(a) Find the electric ﬁeld at an arbitrary point in space.

(b) Now let the length go to inﬁnity and ﬁnd a closed-form expression for the

ﬁeld in (a). You will have to look up the integral in an integral table.

cylinder.

4.33. A uniformly charged disk of radius a and surface charge density σ is

inthe xy-plane with its center at the origin and is rotating about its perpen-

dicular axis with angular frequency ω.

(a) Find the cylindrical components of the magnetic ﬁeld produced at a point

P =(ρ, 0,z) as double integrals in cylindrical coordinates.

(b) Now assume that P is on the z-axis and ﬁnd the components of B by

performing all the integrals involved.

136 Integration: Applications

4.34. An electrically charged disk of radius a is rotating about its perpen-

dicular axis with angular frequency ω. Its surface charge density is given in

cylindrical coordinates by σ =(σ

)ρ

,whereσ

is a constant.

(a) Find the Cartesian components of the magnetic ﬁeld produced at an ar-

bitrary point P =(ρ, 0,z) as double integrals in cylindrical coordinates.

(b) Now assume that P is on the z-axis and ﬁnd the components of B by

performing all the integrals involved.

4.35. Express the components of g of Example 4.2.4 in Cartesian and cylin-

drical coordinates in terms of integrals similar to Equation (4.33).

4.36. A conic surface of (maximum) radius a and half-angle α is uniformly

charged with surface density σ.

(a) Find the three components of the electric ﬁeld at a point on the cone’s axis

adistancer from its vertex. Express your answers in terms of single integrals

in an appropriate coordinate system.

(b) Find the components of the ﬁeld at r = a/

√

3whenα = π/6. By eval-

uating integrals numerically if necessary, express your answer as a numerical

multiple of k

σ.

4.37. A cone with half-angle α, the distance of whose vertex from its circular

rim is L, is rotating with angular speed ω about its axis. Electric charge

is distributed uniformly on the cone with surface charge density σ.Usethe

coordinate system appropriate for this geometry.

(a) Express the components of the magnetic ﬁeld produced at an arbitrary

point in space in terms of double integrals. Evaluate those components whose

integrals are easily done.

(b) Move the ﬁeld point to the axis of the cone, and write the components

of the ﬁeld in terms of single integrals. Evaluate the remaining components

whose integrals are easily done.

axis at a distance L from the vertex of the cone as a number times k

ωσL.

4.38. A uniformly charged solid cylinder of length L,radiusa, and total

charge q is rotated about its axis with angular speed ω. Find the magnetic

ﬁeld at a point on this axis.

4.39. Use cylindrical coordinates to calculate the gravitational ﬁeld of the

hemisphere of Example 4.3.1 at a point on the z-axis.

(a) Show that

=2πGρ

(



+ a

−|z|−

+ z

)

3/2

−|a − z|(a

+ z

+ az)

)

with the other components being zero.

(b) Simplify this expression for points outside (z<0andz>a), and inside

(0 <z<a).

ﬂat side points up.

(d) Add the results of (b) and (c) to ﬁnd the ﬁeld of a full sphere.

4.4 Problems 137

Figure 4.22: The segment of a cylinder with uniform charge density used in Problem

4.41.

4.40. Find the moment of inertia of a uniform solid cone of mass M and

half-angle α cut out of a solid sphere of radius a. What is the moment of

inertia of a whole solid sphere?

4.41. A solid cylinder of length L has a cross section which is in the shape

of a segment of an annular ring with outer radius b and inner radius a.It

is subtended by an angle α and is uniformly charged with total charge q

(Figure 4.22). Find the electric ﬁeld at:

(a) an arbitrary point in space; and

(b) a point on the axis of the ring.

(d) What is the answer to (a) if we have a complete ring that is inﬁnitely

long? Consider the three regions: ρ ≤ a, a ≤ ρ ≤ b,andρ ≥ b.

4.42. Find the moment of inertia of the (incomplete) cylinder of the previous

problem about the perpendicular axis passing through the common center of

the inner and outer radii. Assume that the total mass is M . From this result

obtain the moment of inertia of a hollow as well as a solid cylinder.

Chapter 5

Dirac Delta Function

Paul Adrian Maurice Dirac, one of the most inventive mathematical physicists

of all time, co-founder of quantum theory, inventor of relativistic quantum

mechanics in the form of an equation which bears his name, predictor of the

existence of anti-matter, clariﬁer of the concept of spin, and contributor to the

unraveling of the mathematical diﬃculties associated with the quantization

of the general theory of relativity, came across the subject matter of this

chapter in his study of quantum mechanical scattering. In order to appreciate

the usefulness of this function, we shall start with an intuitive approach drawn

from electrostatics.

5.1 One-Variable Case

Consider a straight linear charge distribution of length L with uniform charge

density as shown in Figure 5.1(a). If the total charge of the line segment is q,

then the linear charge density will be λ = q/L. We are interested in the graph

of the function describing the linear density in the interval (−∞, +∞). As-

suming that the midpoint of the segment is x

and its length L, we can easily

draw the graph of the function. This is shown in Figure 5.1(b). The graph

q/L

(a)

(b)

Figure 5.1: (a) The charged line segment and (b) its linear density function.

140 Dirac Delta Function

is that of a function that is zero for values less than x

− L/2, q/L for val-

ues between x

− L/2andx

+ L/2, and zero again for values greater than

+ L/2. Let us call this function λ(x). Then, we can write

λ(x)=

⎧

⎪

⎨

⎪

⎩

0ifx<x

− L/2,

q/L if x

− L/2 <x<x

+ L/2,

0ifx>x

+ L/2.

Now suppose that we squeeze the segment on both sides so that the length

shrinks to L/2 without changing the position of the midpoint and the amount

of charge. The new function describing the linear charge density will now be

λ(x, x

)=q

⎧

⎪

⎨

⎪

⎩

0ifx<x

− L/4,

2/L if x

− L/4 <x<x

+ L/4,

0ifx>x

+ L/4.

We have “factored out” q for later convenience. We have also introduced a

second argument to emphasize the dependence of the function on the mid-

point. Instead of one-half, we can shrink the segment to any fraction, still

keeping both the amount of charge and the midpoint unchanged. Shrinking

the size to L/n and renaming the function λ

(x, x

) to reﬂect its dependence

on n,gives

(x, x

)=q

⎧

⎪

⎨

⎪

⎩

0ifx<x

− L/2n,

n/L if x

− L/2n<x<x

+ L/2n,

0ifx>x

+ L/2n,

which is depicted in Figure 5.2 for n = 10 as well as some smaller values of n.

The important property of λ

(x, x

) is that its height increases at the same

time that its width decreases.

Instead of a charge distribution that abruptly changes from zero to some

ﬁnite value and just as abruptly drops to zero, let us consider a distribution

Figure 5.2: The linear density function as the length shrinks.

5.1 One-Variable Case 141

that smoothly rises to a maximum value and just as smoothly falls to zero.

There are many functions describing such a distribution. For example,

(x, x

)=q



−n(x−x

)

has a peak of q



n/π at x = x

and drops to smaller and smaller values as

we get farther and farther away from x

in either direction. This function is

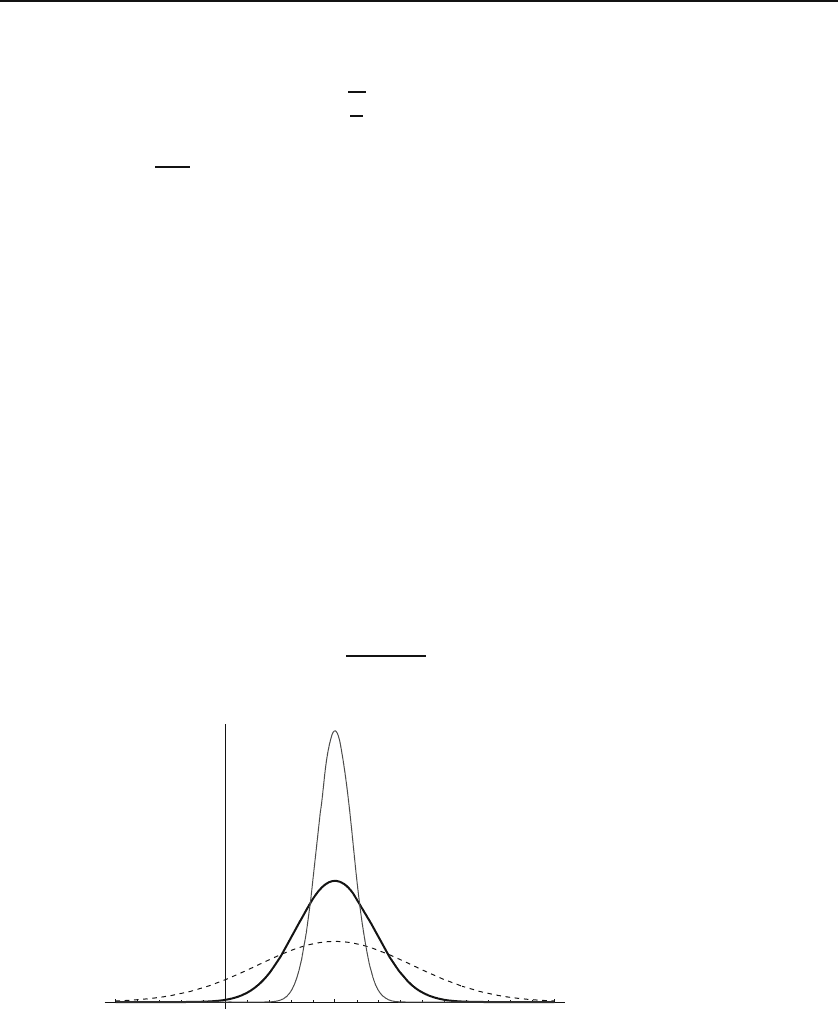
plotted for various values of n in Figure 5.3. It is clear from the ﬁgure that

the “width” of the graph of λ

(x, x

) gets smaller as n →∞.

In both cases λ

(x, x

) is a true linear (charge) density in the sense that

its integral gives the total charge. This is evident in the ﬁrst case because

of the way the function was deﬁned. In the second case, once we integrate

(x, x

) from −∞ to +∞, we also obtain the total charge q. The region of

integration extends over all real numbers in the second case because at every

point of the real line we have some nonzero charge. Furthermore, we can

extend the interval of integration over all the real numbers even for the ﬁrst

case, because the function vanishes outside the interval (x

−L/2n, x

+L/2n)

and no extra contribution to the integral arises. We thus write

+∞

−∞

(x, x

) dx = q

for all such functions. It is convenient to divide by q and deﬁne new functions

(x, x

)by

(x, x

) ≡

(x, x

)

–1

1 2 3

Figure 5.3: The Gaussian bell-shaped curve approaches the Dirac delta function as the

width of the curve approaches zero. The value of n is 1 for the dashed curve, 4 for the

heavy curve, and 20 for the light curve.

142 Dirac Delta Function

so that

(x, x

⎧

⎪

⎨

⎪

⎩

0ifx<x

− L/2n,

n/L if x

− L/2n<x<x

+ L/2n,

0ifx>x

+ L/2n,

in the ﬁrst case, and

(x, x



−n(x−x

)

(5.1)

in the second case. Both these functions have the property that

+∞

−∞

(x, x

) dx =1, (5.2)

i.e., their integral over all the real numbers is one, and, in particular, inde-

pendent of n.

Dirac delta

function deﬁned

Box 5.1.1. The Dirac delta function δ(x, x

) is deﬁned as

δ(x, x

) ≡ lim

n→∞

(x, x

) (5.3)

and has the following property:

+∞

−∞

δ(x, x

) dx =1. (5.4)

Equation (5.4) follows from the fact that the integral in (5.2) is independent

of n. The Dirac delta function has inﬁnite height and zero width at x

, but

these two undeﬁned quantities compensate for one another to give a ﬁnite area

under the “graph” of the function. The Dirac delta function is not a well-

behaved mathematical function as deﬁned in elementary textbooks because at

the only point that it is nonzero, it is inﬁnite! Nevertheless, this function has

been investigated rigorously in higher mathematics. For us, the Dirac delta

function is a convenient way of describing densities.

Although we have separated the arguments of the Dirac delta function

by a comma, the function depends only on the diﬀerence between the two

arguments. This becomes clear if we think of the Dirac delta function as the

limit of the exponential because the latter is a function of x−x

. We therefore

have the important relation

δ(x, x

)=δ(x −x

). (5.5)

In particular, since the delta function becomes inﬁnite at x = x

,wehave

δ(x, x

)



x=x

= δ(x −x

)



x=x

= δ(0) = ∞. (5.6)