Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


5.1 One-Variable Case 153
Because θ is constant everywhere except at 0, its derivative is zero ev-
erywhere except at 0. The discontinuity at 0 makes the derivative infinite
there:
step function and
its relation to
delta function
θ
(0) = lim
→0
θ() − θ(−)
2
= lim
→0
1 − 0
2
→∞
This strongly suggests the identification of the derivative of the step function
as the Dirac delta function. In fact, noting that
θ(x − x
0
)=
0
1ifx>x
0
0ifx<x
0
,
(5.19)
and the fact that θ
(x − x
0
) is zero everywhere except at x
0
, for any well-
behaved function f(x)weobtain
#
∞
−∞
f(x)θ
(x − x
0
) dx =
#
x
0
+
x
0
−
f(x)θ
(x − x
0
) dx ≈ f(x
0
)
#
x
0
+
x
0
−
θ
(x − x
0
) dx
= f(x
0
) θ(x − x
0
)|
x
0
+
x
0
−
= f(x
0
)[θ()
=1
−θ(−)
=0
]=f(x
0
)
We thus have another important representation of the Dirac delta function:
δ(x −x
0
)=θ
(x −x
0
) (5.20)
Example 5.1.6.
For positive a,tanh(ax)goesto1asx →∞and to −1as
x →−∞and it makes a smooth transition from one of these asymptotic values to
the other. This transition gets steeper and steeper for larger and larger values of a.
This suggests the following relation:
θ(x − x
0
)=
1
2
lim
a→∞
{1 + tanh[a(x − x
0
)]}
Let θ
a
(x − x
0
) stand for the function on the right-hand side for any finite positive
a.Then
θ
a
(x − x
0
)=
1
2
d
dx
{1+tanh[a(x − x
0
)]} =
a sech
2
[a(x − x
0
)]
2
and
#
∞
−∞
θ
a
(x − x
0
) dx = θ
a
(x − x
0
)|
∞
−∞
=
1
2
{1+tanh[a(x − x
0
)]}|
∞
−∞
=1
for any value of a>0, in particular for a →∞. Thus, we get yet another represen-
tation of the Dirac delta function:
δ(x − x
0
) = lim
a→∞
θ
a
(x − x
0
) = lim
a→∞
a sech
2
[a(x − x
0
)]
2

154 Dirac Delta Function
5.2 Two-Variable Case
We can generalize the discussion of the previous section to the case of many
variables. For example, in two dimensions using Cartesian coordinates, we
can define the functions δ
n
as
δ
n
(x −x
0
,y−y
0
)=Ce
−n
.
(x−x
0
)
2
+(y−y
0
)
2
/
= Ce
−n(x−x
0
)
2
e
−n(y−y
0
)
2
, (5.21)
where C is a constant to be determined in such a way as to make the integral
of δ
n
over the entire xy-plane equal to one. A simple calculation will show
that C = n/π. This constant is simply the product of two “one-dimensional
constants”: one for the exponential in x and the other for the exponential in y.
This is as expected, because δ
n
(x −x
0
,y−y
0
)isdefined to be the product of
two one-dimensional δ
n
’s. Such a simplicity is the result of the coordinate sys-
tems we have used and does not prevail in other—non-Cartesian—coordinate
systems, for which the constant C must be evaluated separately.
It should be clear from (5.21) that as n increases, the height of δ
n
at
(x
0
,y
0
) increases while its width decreases (see Figure 5.5). What may not be
clear is that this reciprocal behavior takes place in such a way as to keep the
volume under the surface equal to one. We can define—as we did in the one
dimensional case—a surface density function as a function whose integral
surface density
function
over the entire plane is one. For any n, then, δ
n
will be a surface density
function.
The passage to the two-dimensional Dirac delta function is now clear:
two-dimensional
Dirac delta
function
δ(x −x
0
,y− y
0
) ≡ lim
n→∞
δ
n
(x − x
0
,y− y
0
). (5.22)
The two-dimensional Dirac delta function above is zero everywhere except at
(x
0
,y
0
) where it is infinite. Thus for the Dirac delta function not to be zero
both of its arguments must be zero. It is convenient to define points P and P
0
Figure 5.5: As n gets larger and larger, the two-dimensional Gaussian exponential
approaches the two-dimensional Dirac delta function. For the left bump, n = 400;for
the middle, n = 1000; and for the right spike n = 4000.
5.2 Two-Variable Case 155
with respective Cartesian coordinates (x, y)and(x
0
,y
0
), and position vectors
r = x, y, r
0
= x
0
,y
0
,andwrite
δ(x −x
0
,y− y
0
) ≡ δ(r − r
0
)=
0
δ(
0) ≡ δ(0, 0) = ∞ if r = r
0
,
0otherwise.
(5.23)
This means
Box 5.2.1. The two-dimensional Dirac delta function is zero everywhere
except at the point which makes both of its arguments zero, in which case
the two-dimensional Dirac delta function is infinite.
We noted above that in Cartesian coordinates—and only in Cartesian
coordinates—the product of two one-dimensional δ
n
’sgaverisetoatwo-
dimensional δ
n
which subsequently yielded the two-dimensional Dirac delta
function. Thus only in Cartesian coordinates can we conclude that
δ(r −r
0
)=δ(x −x
0
,y− y
0
)=δ(x −x
0
) δ(y − y
0
). (5.24)
We shall see that in polar coordinates, the two-dimensional delta function
is not merely the product of two one-dimensional delta functions, but some
other factor is also present.
The density property of the two-dimensional Dirac delta function survives
the n →∞process because the integral of δ
n
is independent of n.Onthe
other hand, the delta function is zero everywhere except at the point which
makes both of its arguments zero. Therefore, for any two-dimensional region
Ω, we have
##
Ω
δ(r −r
0
) da(r)=
0
1ifP
0
is in Ω,
0otherwise.
(5.25)
Equation (5.25) is written independently of coordinates, and as such, the
vector arguments are to be interpreted as coordinates not components. We
can use this equation in polar coordinates to write the two-dimensional Dirac
delta function as a product of two one-dimensional delta functions. First
write
2
δ(r −r
0
)=Cδ(ρ − ρ
0
)δ(ϕ −ϕ
0
).
2
We use ρ and ϕ instead of the more common r and θ because we have reserved the
latter for the three-dimensional spherical coordinates. There is no danger of confusing the
pair (ρ, ϕ) with the corresponding pair in cylindrical coordinates because the two pairs are
identical.
156 Dirac Delta Function
Now substitute this in Equation (5.25) with Ω being the entire plane, and
note that da = ρdρdϕ:
1=
##
Ω
Cδ(ρ −ρ
0
)δ(ϕ −ϕ
0
) ρdρdϕ
= C
#
∞
0
δ(ρ − ρ
0
)ρdρ
#
2π
0
δ(ϕ −ϕ
0
) dϕ
=1
= Cρ
0
⇒ C =
1
ρ
0
.
In the above derivation, we have used properties of the one-dimensional delta
function as applied to δ(ρ −ρ
0
)andδ(ϕ − ϕ
0
).
Box 5.2.2. The two-dimensional Dirac delta function can be written in
polar coordinates as
δ(r −r
0
)=
1
ρ
0
δ(ρ − ρ
0
)δ(ϕ −ϕ
0
)=
1
ρ
δ(ρ −ρ
0
)δ(ϕ −ϕ
0
). (5.26)
The last equality follows because the Dirac delta function in ρ forces ρ and
ρ
0
to be equal.
A collection of point physical quantities Q
1
,Q
2
,...,Q
n
located on a sur-
face can be described by a surface density σ
Q
(r) using the two-dimensional
Dirac delta function:
surface density
and
two-dimensional
delta function
σ
Q
(r)=
n
k=1
Q
k
δ(r −r
k
), (5.27)
where r
k
is the position vector of Q
k
. This equation can be rewritten as
σ
Q
(x, y)=
n
k=1
Q
k
δ(x −x
k
)δ(y − y
k
)
in Cartesian coordinates, and as
σ
Q
(ρ, ϕ)=
n
k=1
Q
k
ρ
k
δ(ρ −ρ
k
)δ(ϕ −ϕ
k
)=
1
ρ
n
k=1
Q
k
δ(ρ − ρ
k
)δ(ϕ −ϕ
k
)
in polar coordinates.
Example 5.2.1.
With an appropriate choice of the origin and the axes of a Carte-
sian coordinate system, the surface charge density for four charges q
1
,q
2
,q
3
,q
4
lo-
cated at the four corners of a square of sides 2a can be written as
σ
q
(x, y)=
4
k=1
q
k
δ(x − x
k
)δ(y − y
k
)
= q
1
δ(x − a)δ(y −a)+q
2
δ(x + a)δ(y −a)
+ q
3
δ(x + a)δ(y + a)+q
4
δ(x − a)δ(y + a).
5.2 Two-Variable Case 157
If polar coordinates are used, the surface charge density becomes
σ
q
(ρ, ϕ)=
4
k=1
q
k
ρ
k
δ(ρ − ρ
k
)δ(ϕ − ϕ
k
)
=
δ(ρ −
√
2 a)
√
2 a
3
q
1
δ(ϕ − π/4) + q
2
δ(ϕ − 3π/4)
+ q
3
δ(ϕ − 5π/4) + q
4
δ(ϕ − 7π/4)
4
.
The reader is urged to study these two equations carefully and make sure to under-
stand the details of their derivation.
A more interesting example is the two-dimensional ionic crystal.
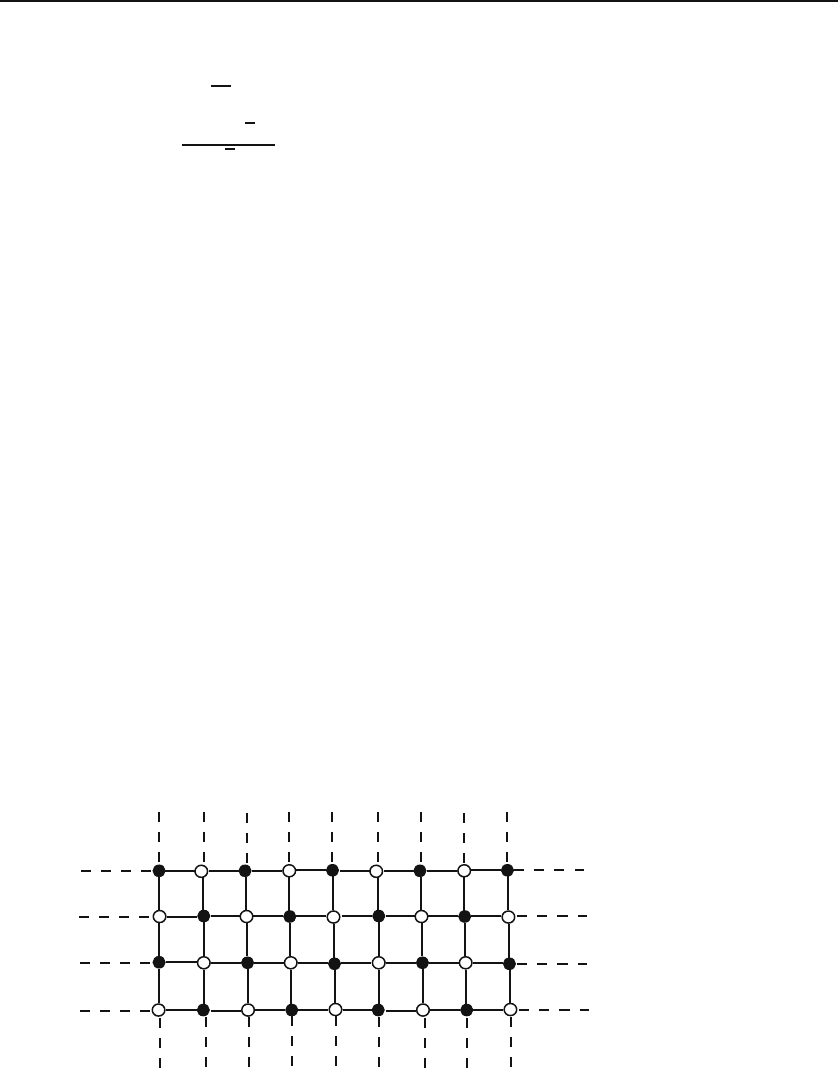
Example 5.2.2.
Suppose positive and negative charges ±q are arranged on an
infinite square grid in such a way that the nearest neighbors of each charge have
charges of opposite sign, i.e., charges alternate both horizontally and vertically (see
Figure 5.6). Assume that the distance between each charge and its nearest neighbor
is a, and that we place our Cartesian origin at the location of a positive charge.
Then the surface charge density can be written as two-dimensional
ionic crystal
σ
q
(x, y)=q
∞
i=−∞
∞
j=−∞
(−1)
i+j
δ(x − ia)δ(y − ja).
For a finite 2M × 2N grid one substitutes the first infinity with M and the second
one with N. Similarly, one can consider rectangular units of sides a and b for the
grid. Then one should change the second argument of the delta function (or the
argument of the delta function corresponding to y)toy − jb.
With an extra dimension at our disposal, we can invent many new vari-
eties of distribution of point physical quantities that were not possible in one
dimension. For example, we can put the points on a curve in the xy-plane.
It is instructive to find the surface density of such a collection of points. The
following example examines this problem.
Figure 5.6: A two-dimensional ionic crystal.
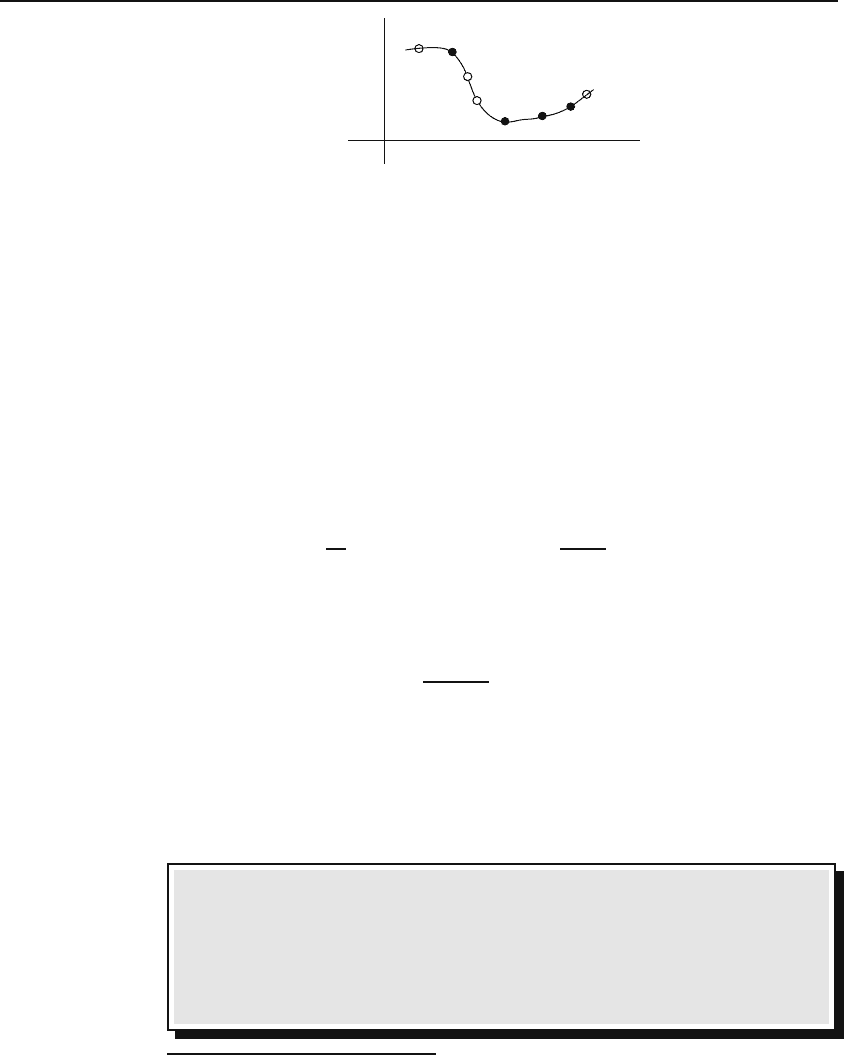
158 Dirac Delta Function
x
y
Figure 5.7: Point charges located on a curve in the xy-plane.
Example 5.2.3. For concreteness, we consider n point charges located at n points
{P
k
}
n
k=1
with P
k
having Cartesian coordinates (x
k
,y
k
). These points are assumed
to be on a curve with the Cartesian equation y = f(x) as shown in Figure 5.7. The
surface charge density in Cartesian coordinates becomes
σ
q
(x, y)=
n
k=1
q
k
δ(x − x
k
)δ(y − y
k
)=
n
k=1
q
k
δ(x − x
k
)δ
y − f(x
k
)
.
If the curve is given as ρ = g(ϕ), then polar coordinates are more appropriate,
and the surface charge density will be
3
σ
q
(ρ, ϕ)=
n
k=1
q
k
ρ
k
δ(ρ − ρ
k
)δ(ϕ − ϕ
k
)=
n
k=1
q
k
g(ϕ
k
)
δ(ρ − g(ϕ
k
)) δ(ϕ − ϕ
k
).
For instance, if the charges are located on a circle of radius a each separated from
its nearest neighbor by an angle α, with the first charge on the x-axis, then
σ
q
(ρ, ϕ)=
δ(ρ − a)
a
n
k=1
q
k
δ(ϕ − (k − 1)α),
wherewehaveusedthefactthatg(ϕ)=a for a circle of radius a.
All the properties of the delta function can be generalized to two dimen-
sions. One important property is given in Equation (5.10).
Box 5.2.3. Let Ω be a region in the xy-plane and P
0
a point there; then
##
Ω
f(r)δ(r − r
0
) da =
0
f(r
0
) ≡ f(x
0
,y
0
) if P
0
is in Ω,
0 otherwise,
(5.28)
where (x
0
,y
0
) are the Cartesian coordinates of P
0
.
3
Because of the two delta functions, one can substitute ρ for ρ
k
and ϕ for ϕ
k
in the
denominators.
5.3 Three-Variable Case 159
Differentiating both sides with respect to the first argument x
0
, we easily
obtain the analog of Equation (5.12):
##
Ω
f(r)∂
1
δ(r −r
0
) da =
0
−∂
1
f(r
0
) ≡−∂
1
f(x
0
,y
0
)ifP
0
is in Ω,
0otherwise,
with a similar relation for differentiation with respect to the second argument.
We can combine the two relations into a single relation:
Box 5.2.4. The derivative of the Dirac delta function in two dimensions
satisfies
##
Ω
f(r)∂
i
δ(r −r
0
) da =
0
−∂
i
f(r
0
) ≡−∂
i
f(x
0
,y
0
) if P
0
is in Ω,
0 otherwise,
where i can be 1 or 2, ∂
1
= ∂
x
and ∂
2
= ∂
y
.
5.3 Three-Variable Case
Once the generalization to two variables is realized, the three—and more—
variable cases become trivial. In fact, we had such generalizations in mind
when we wrote most of the formulas in the last section: All that is needed
is to change da to dV and keep in mind that the vectors r and r
0
have
three components, and points in space have three coordinates. Nevertheless,
we shall summarize the most important properties of the three-dimensional
Dirac delta function.
First we note that
δ(r −r
0
)=
0
δ(
0) ≡ δ(0, 0, 0) = ∞ if r = r
0
,
0otherwise.
(5.29)
This means
Box 5.3.1. The three-dimensional Dirac delta function is zero everywhere
except at the point which makes all three of its arguments zero in which
case it is infinite.
In Cartesian coordinates, we have 3D Dirac delta
function in
Cartesian
coordinates
δ(r −r
0
)=δ(x −x
0
,y− y
0
,z− z
0
)
= δ(x −x
0
) δ(y − y
0
) δ(z − z
0
). (5.30)
160 Dirac Delta Function
An argument similar to the two-dimensional case can be used to show that3D Dirac delta
function in
cylindrical and
spherical
coordinates
Box 5.3.2. In cylindrical coordinates
δ(r −r
0
)=
1
ρ
0
δ(ρ −ρ
0
)δ(ϕ −ϕ
0
)δ(z − z
0
), (5.31)
where r and r
0
ontheLHSaretobeunderstoodascylindricalcoordi-
nates, not cylindrical position vectors. The corresponding formula for the
spherical coordinate system is
δ(r −r
0
)=
1
r
2
0
sin θ
0
δ(r − r
0
)δ(θ − θ
0
)δ(ϕ −ϕ
0
), (5.32)
with r and r
0
representing the coordinates (r, θ, ϕ) and (r
0
,θ
0
,ϕ
0
),re-
spectively.
The density property of the three-dimensional Dirac delta function is given
by
##
Ω
δ(r −r
0
) dV (r)=
0
1ifP
0
is in Ω,
0otherwise,
(5.33)
where Ω is a region of space and P
0
is the point with Cartesian coordi-
nates (x
0
,y
0
,z
0
), spherical coordinates (r
0
,θ
0
,ϕ
0
), and cylindrical coordinates
(ρ
0
,ϕ
0
,z
0
). Similarly,
Box 5.3.3. If Ω is a region of space, then for a “good” function f(r),
##
Ω
f(r)δ(r − r
0
) dV (r)=
0
f(r
0
) if P
0
is in Ω,
0 otherwise.
Thus integration reduces to the evaluation of the function f at the coordi-
nates of P
0
.
The density property allows us to write the distribution of discrete physical
quantities in terms of the three-dimensional Dirac delta function. In general,
volume density
and 3D delta
function
ρ
Q
(r)=
n
k=1
Q
k
δ(r −r
k
) (5.34)
which can be rewritten as
ρ
Q
(x, y, z)=
n
k=1
Q
k
δ(x −x
k
)δ(y − y
k
)δ(z − z
k
)

5.3 Three-Variable Case 161
in Cartesian coordinates, as
ρ
Q
(ρ, ϕ, z)=
n
k=1
Q
k
ρ
k
δ(ρ −ρ
k
)δ(ϕ −ϕ
k
)δ(z − z
k
)
in cylindrical coordinates, and as
ρ
Q
(r, θ, ϕ)=
n
k=1
Q
k
r
2
k
sin θ
k
δ(r − r
k
)δ(θ − θ
k
)δ(ϕ −ϕ
k
)
in the spherical coordinate system. In fact, the linear and surface distributions
of a physical quantity involving the Dirac delta function are special cases of
the volume distribution. For instance, a collection of point quantities in the
xy-plane can be described by the volume density
ρ
Q
(x, y, z)=
n
k=1
Q
k
δ(x −x
k
)δ(y − y
k
)δ(z)
= δ(z)
n
k=1
Q
k
δ(x −x
k
)δ(y − y
k
).
The delta function outside the sum restricts the z-coordinates of point quan-
tities to zero, and thus their location, to the xy-plane. Similarly,
ρ
Q
(r, θ, ϕ)=
δ(r − a)
a
2
n
k=1
Q
k
sin θ
k
δ(θ − θ
k
)δ(ϕ −ϕ
k
)
describes a distribution of n point quantities on a sphere of radius a.
Example 5.3.1.
Let us calculate the electrostatic field of the one-dimensional
infinite ionic crystal in Cartesian coordinates. Assume that the charges are located
on the z-axis (Figure 5.8). We treat this as a three-dimensional charge distribution
with density
ρ
q
(x, y, z)=q
∞
k=−∞
(−1)
k
δ(x)δ(y)δ(z −ka). (5.35)
x
y
z
P
Figure 5.8: The geometry for the calculation of the electrostatic field of the one-
dimensional ionic crystal.
162 Dirac Delta Function
The first two delta functions restrict the charges to the z-axis and the third locates
them. This density is to be substituted in the equation for the electric field in
Cartesian coordinates. Let us concentrate on the x-component
E
x
(x, y, z)=k
e
##
Ω
ρ
q
(x
,y
,z
)(x − x
) dx
dy
dz
{(x − x
)
2
+(y − y
)
2
+(z − z
)
2
}
3/2
.
We can always take Ω to be the entire space because the delta function will restrict
the integration to the region of charges automatically. We can also choose our
coordinate system so that the field point lies in the xz-plane, i.e., y =0. Notethat
we have to prime all the arguments of ρ
q
before we substitute it in the integral.
Having done this, we obtain
E
x
(x, y, z)=k
e
q
∞
k=−∞
(−1)
k
##
Ω
(x − x
)δ(x
)δ(y
)δ(z
− ka) dx
dy
dz
{(x − x
)
2
+ y
2
+(z − z
)
2
}
3/2
.
Using Box 5.3.3, noting that
f(x
,y
,z
)=
(x − x
)
{(x − x
)
2
+ y
2
+(z − z
)
2
}
3/2
,
and that the result of integration is the evaluation of f at x
=0=y
, z
= ka,we
obtain
E
x
(x, y, z)=k
e
q
∞
k=−∞
(−1)
k
x
{x
2
+(z − ka)
2
}
3/2
= k
e
q
−1
k=−∞
(−1)
k
x
{x
2
+(z − ka)
2
}
3/2
+ k
e
q
x
(x
2
+ z
2
)
3/2
+ k
e
q
∞
k=+1
(−1)
k
x
{x
2
+(z − ka)
2
}
3/2
,
wherewehavebrokenupthesummationintothreepieces,apermissibleactaslong
as the series converges. We can combine the first and third terms by changing k to
−k in the first and noting that
(−1)
−k
=
1
(−1)
k
=(−1)
k
.
Doing so, we get
E
x
(x, 0,z)=k
e
q
x
(x
2
+ z
2
)
3/2
+ k
e
q
∞
k=1
(−1)
k
x
{x
2
+(z + ka)
2
}
3/2
+
x
{x
2
+(z − ka)
2
}
3/2
.
The other components of the field can be found similarly:
E
y
(x, 0,z)=0,
E
z
(x, 0,z)=k
e
q
z
(x
2
+ z
2
)
3/2
(5.36)
+ k
e
q
∞
k=1
(−1)
k
z + ka
{x
2
+(z + ka)
2
}
3/2
+
z − ka
{x
2
+(z − ka)
2
}
3/2
.
