Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


184 Planar and Spatial Vectors
These all indicate that we are on the right track.
We also note that the inner product depends on the interval chosen on the real
line. For different (a, b), we get a different inner product. The choice is usually
dictated by the physical application. We shall choose a =0,b = 1, although this
may not be a physically suitable choice. With such a choice and with {f
1
=1, f
2
= t}
as a basis, we obtain
g
11
= f
1
· f
1
=
#
1
0
f
1
(t)f
1
(t) dt =
#
1
0
dt =1,
g
12
= f
1
· f
2
=
#
1
0
f
1
(t)f
2
(t) dt =
#
1
0
tdt =
1
2
= g
21
,
g
22
= f
2
· f
2
=
#
1
0
f
2
(t)f
2
(t) dt =
#
1
0
t
2
dt =
1
3
.
So the inner product matrix is
G =
1
1
2
1
2
1
3
.
We started with Equation (1.1) as the definition of the inner product. This
definition assumed a knowledge of lengths and angles. These are notions with
which we become intuitively familiar very early in our mental development.
the notion of
length comes after
that of the inner
product!
However, such notions are not intuitively obvious for two polynomials. That
is why the concepts of lengths and angles for objects such as polynomials
come after introducing the notion of inner product. Of course, we want these
notions to agree with the intuitive notions of lengths and angles, i.e., we want
them to be related to the inner product in precisely the same manner as given
in Equation (1.1). If we let b = a in that equation, we get a ·a = |a|
2
.This
becomes our definition for length:
Box 6.1.5. Given any inner product on a set of objects that we can call
“vectors,” we define the length of a vector a as |a|≡+
√
a ·a.
Once the notion of length is established for a general set of vectors, we
can define the angle between two vectors a and b as
cos θ ≡
a ·b
|a||b|
=
a ·b
√
a ·a
√
b · b
. (6.18)
This equation and the one in Box 6.1.5 clearly show that lengths and angles
are given entirely in terms of inner products. For these concepts to be valid,
we must ensure that however we define the inner product, it will have the
property that a · a > 0 for a nonzero vector. It turns out that most inner
products encountered in applications have this property. Nevertheless, there
6.1 Vectors in a Plane Revisited 185
are cases (very important ones) for which a·a ≤ 0. In such cases, the concepts in some important
physical situations
the “length” of a
nonzero vector
can be zero—even
negative!
of length and angles, as we know them, break down, and we have to be content
with “dot products” that may produce nonpositive numbers when a nonzero
vector is “dotted” with itself.
Even if a ·a > 0, there is no a priori guarantee that the cosine obtained in
Equation (6.18) will lie between −1 and +1, as it should. However, there is
a famous inequality in mathematics called the Schwarz inequality,which
establishes this fact for those inner products which satisfy a ·a > 0. We shall
come back to this later in this chapter.
Example 6.1.8.
The lengths of the basis vectors {f
1
=1, f
2
= t} of P
1
[t]canbe
found easily using the results of Example 6.1.7:
|f
1
| =
√
f
1
· f
1
=+
√
1=1
|f
2
| =
√
f
2
· f
2
=+
1
3
.
We can also find the “angle” between the two polynomials
cos θ =
f
1
· f
2
|f
1
||f
2
|
=
1
2
1 · (1/
√
3)
=
√
3
2
⇒ θ =
π
6
.
The matrix G, called the inner product matrix or metric matrix, G is the inner
product matrix or
the metric matrix.
completely determines the inner product of vectors when they are written
as linear combinations of a
1
and a
2
. For example, consider a vector a with
components (α
1
,α
2
) in the basis {a
1
, a
2
}. Figure 6.3 shows a as the sum of
−→
OA (which is the same as α
1
a
1
)and
−−→
OA
(which is the same as α
2
a
2
). Using
the law of cosines for the triangle OAP,weget
|a|
2
= OP
2
= OA
2
+ AP
2
− 2OA AP cos ϕ
= α
2
1
|a
1
|
2
+ α
2
2
|a
2
|
2
+2α
1
α
2
|a
1
||a
2
|cos θ
12
.
θ
12
θ
12
θ
a
b
a
1
a
2
a
1
a
2
O
A
B
P
ϕ
'
A
Figure 6.3: The length of a is the same whether we use the law of cosine or the inner
product matrix G.

186 Planar and Spatial Vectors
On the other hand, using Equation (6.16), we obtain
|a|
2
= a · a =
α
1
α
2
!
g
11
g
12
g
21
g
22
α
1
α
2
=
α
1
α
2
!
g
11
α
1
+ g
12
α
2
g
21
α
1
+ g
22
α
2
= g
11
α
2
1
+2g
12
α
1
α
2
+ g
22
α
2
2
= a
1
· a
1
α
2
1
+2α
1
α
2
a
1
·a
2
+ a
2
·a
2
α
2
2
= |a
1
|
2
α
2
1
+2α
1
α
2
|a
1
||a
2
|cos θ
12
+ |a
2
|
2
α
2
2
and the two expressions agree. In fact, we can show this agreement very
generally:
a ·b =(α
1
a
1
+ α
2
a
2
) ·(β
1
a
1
+ β
2
a
2
)
= α
1
β
1
a
1
· a
1
+ α
1
β
2
a
1
·a
2
+ α
2
β
1
a
2
·a
1
+ α
2
β
2
a
2
· a
2
= α
1
β
1
g
11
+ α
1
β
2
g
12
+ α
2
β
1
g
21
+ α
2
β
2
g
22
=
α
1
α
2
!
g
11
g
12
g
21
g
22
β
1
β
2
=
8
aGb,
where we used the distributive property of the inner product.
It should now be clear to the reader that the matrix G contains all the
information needed to evaluate the inner product of any pair of vectors. Sup-
pose now that instead of {a
1
, a
2
} we choose {
ˆ
e
1
,
ˆ
e
2
} where
ˆ
e
1
and
ˆ
e
2
are
unit vectors and perpendicular to one another. Then, the matrix G will have
elements
g
11
=
ˆ
e
1
·
ˆ
e
1
=1,g
12
= g
21
=
ˆ
e
1
·
ˆ
e
2
=0,g
22
=
ˆ
e
2
·
ˆ
e
2
=1,
i.e., G is the unit matrix. In that case, we obtain
8
aGb =
α
1
α
2
!
10
01
β
1
β
2
= α
1
β
1
+ α
2
β
2
which is the usual expression of the dot product of two vectors in terms of
their components. A basis whose vectors have unit length and are mutually
perpendicular to one another is called an orthonormal basis. Thus,
orthonormal basis
Box 6.1.6. Only in an orthonormal basis is the dot (inner) product of two
vectors equal to the sum of the products of their corresponding components.
In such a basis the inner product matrix G is the unit matrix.
The matrix G was introduced to ensure the validity of the inner product
in an arbitrary basis. This poses some restriction on G; for example, we
saw that it had to be symmetric, i.e., g
12
= g
21
because of the symmetry of
the dot product. Another restriction—if we want thedot product of a basis
6.1 Vectors in a Plane Revisited 187
vector with itself to be positive—is that g
11
> 0andg
22
> 0, in which case
the inner product is called positive definite (or Riemannian). It turns
positive definite,
or Riemannian
inner product
out, however, that such a restriction constrains G too much to be useful in
physical applications. Although, in most of this book, we shall adhere to
the usual positive definite or Euclidean inner product, the reader should be
aware that non-Euclidean inner products also have important applications in
physics.
Box 6.1.7. Regardless of the nature of G, we call two vectors a and b
G-orthogonal if a ·b ≡
8
aGb =0.
Every point in the plane can be thought of as the tip of a vector whose
tail is the origin. With this interpretation, we can express the (G-dependent)
distance between two points in terms of vectors. Let r
1
be the vector to point
P
1
and r
2
the vector to point P
2
. Then the “length” of the displacement
vector Δr ≡ r
1
− r
2
is the “distance” between P
1
and P
2
:
P
1
P
2
2
=Δr · Δr =(r
1
− r
2
) ·(r
1
− r
2
)=(
9
Δr)G(Δr). (6.19)
Keep in mind that only in the positive definite (Euclidean) case is
P
1
P
2
2
nonnegative. There are physical situations in which the square of the length
of the displacement vectors can be zero or even negative. We shall encounter
one such example when we discuss the special theory of relativity.
The simplicity of G in orthonormal bases makes them very much in de-
mand. So, it is important to know whether it is always possible to construct
orthonormal vectors out of general basis vectors. The construction should
involve linear combinations only. In other words, given a basis {a
1
, a
2
},we
want to know if there are linear combinations of a
1
and a
2
which are orthonor-
mal. We assume that the inner product is positive definite, so that the inner
product of every nonzero vector with itself is positive. First we divide a
1
by
its length to get
ˆ
e
1
≡
a
1
|a
1
|
=
a
1
√
a
1
· a
1
.
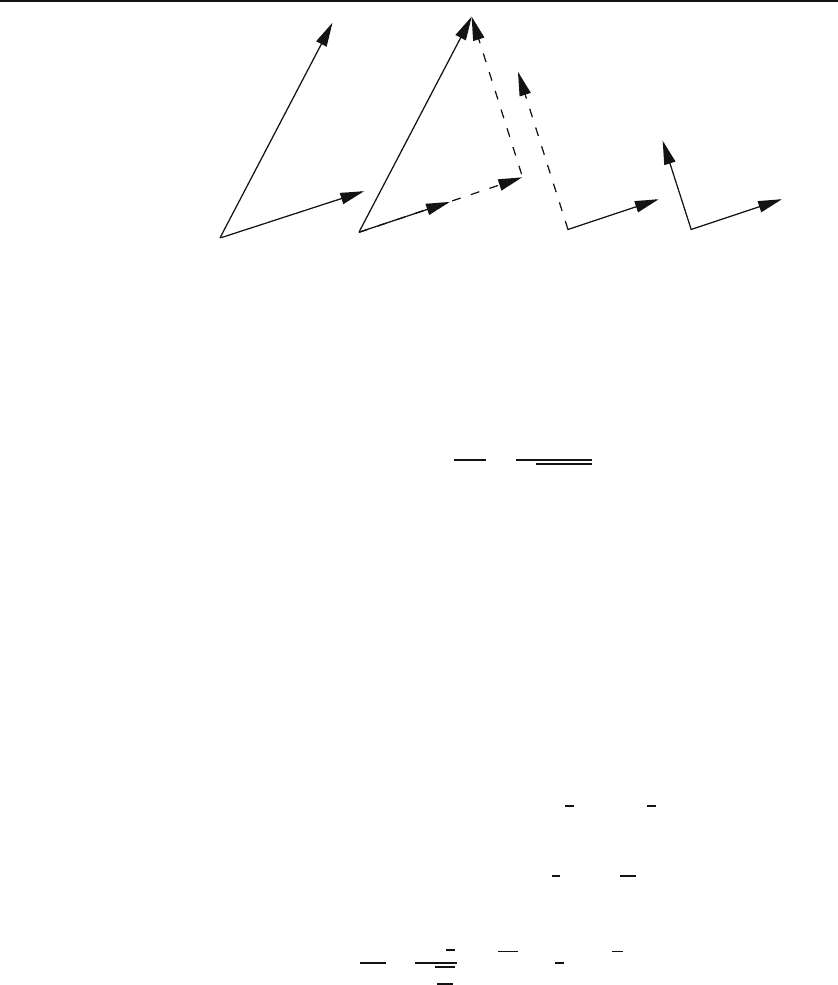
To obtain the second orthonormal vector, we refer to Figure 6.4 which shows
that if we take away from a
2
its projection on a
1
, the remaining vector will
be orthogonal to a
1
.Soconsider
a
2
= a
2
− (a
2
·
ˆ
e
1
)
ˆ
e
1
projection of
a
2
on a
1
and note that Gram–Schmidt
process for the
plane
ˆ
e
1
· a
2
=
ˆ
e
1
·a
2
− (a
2
·
ˆ
e
1
)
ˆ
e
1
·
ˆ
e
1
=1
=0.
188 Planar and Spatial Vectors
(b)(a)
a
1
a
2
e
1
^
a
2
a
2
'
(c)
e
1
^
a
2
'
(d)
e
2
^
e
1
^
Figure 6.4: The illustration of the Gram–Schmidt process for two linearly independent
vectors in the plane.
This suggests defining
ˆ
e
2
as
ˆ
e
2
≡
a
2
|a
2
|
=
a
2
a
2
·a
2
.
The reader should note that in the construction of {
ˆ
e
1
,
ˆ
e
2
}, we have added
vectors and multiplied them by numbers, i.e., we have taken a linear combi-
nation of a
1
and a
2
. This process, and its generalization to arbitrary number
of vectors, is called the Gram–Schmidt process, and shows that by appro-
priately taking linear combinations, it is always possible to find orthonormal
vectors out of any linearly independent set of vectors.
Example 6.1.9.
The basis {1,t} introduced for P
1
[t] is not orthonormal when
the inner product is integration over the interval (0, 1) as in Example 6.1.7. Let us
use the Gram–Schmidt process to find an orthonormal basis. We note that the first
basis vector already has a unit length; so we let
ˆ
e
1
= f
1
= 1. To find the second
vector, we first construct
f
2
= f
2
− (f
2
·
ˆ
e
1
)
ˆ
e
1
= t − (
1
2
)1 = t −
1
2
with
|f
2
|
2
= f
2
· f
2
=
#
1
0
(t −
1
2
)
2
dt =
1
12
.
Then the second vector will be
ˆ
e
2
=
f
2
|f
2
|
=
t −
1
2
1
12
=
√
12(t −
1
2
)=
√
3(2t −1).
The reader may verify directly that {
ˆ
e
1
,
ˆ
e
2
} is an orthonormal basis.
Example 6.1.10. Consider the vectors
a
1
=
ˆ
e
x
+
ˆ
e
y
and a
2
=2
ˆ
e
x
+
ˆ
e
y
.
6.1 Vectors in a Plane Revisited 189
The inner product matrix elements in the basis {a
1
, a
2
} are
g
11
= a
1
· a
1
=(
ˆ
e
x
+
ˆ
e
y
) · (
ˆ
e
x
+
ˆ
e
y
)=2,g
12
=(
ˆ
e
x
+
ˆ
e
y
) · (2
ˆ
e
x
+
ˆ
e
y
)=3,
g
21
= a
2
· a
1
= g
12
=3,g
22
=(2
ˆ
e
x
+
ˆ
e
y
) · (2
ˆ
e
x
+
ˆ
e
y
)=5.
or, in matrix form, G =
23
35
!
.
Now consider vectors b and c,whosecomponentsin{a
1
, a
2
} are, respectively,
(1, 1) and (−3, 2). We can compute the scalar product of b and c in terms of these
components using Equation (6.16):
b · c =
8
bGc =
11
!
23
35
−3
2
=
11
!
0
1
=1.
We can also write b and c in terms of
ˆ
e
x
and
ˆ
e
y
and use the usual definition of
the inner product (in terms of components) to find b·c.Sinceb has the components
(1, 1) in {a
1
, a
2
}, it can be written as
b = a
1
+ a
2
=(
ˆ
e
x
+
ˆ
e
y
)+(2
ˆ
e
x
+
ˆ
e
y
)=3
ˆ
e
x
+2
ˆ
e
y
.
Similarly,
c = −3a
1
+2a
2
= −3(
ˆ
e
x
+
ˆ
e
y
)+2(2
ˆ
e
x
+
ˆ
e
y
)=
ˆ
e
x
−
ˆ
e
y
.
Thus, in {
ˆ
e
x
,
ˆ
e
y
}, b has components (3, 2), and c has components (1, −1). Then
b · c = b
x
c
x
+ b
y
c
y
=3·1+2· (−1) = 1
which agrees with the previous result obtained above.
Example 6.1.11. Consider two vectors f and g in P
1
[t]with
f ≡ f(t)=α
0
+ α
1
t, g ≡ g(t)=β
0
+ β
1
t.
We want to find the inner product of these two vectors. First, we use the basis {1,t}
and its corresponding G matrix found in Example 6.1.7:
f · g = f
t
Gg =
α
0
α
1
!
1
1
2
1
2
1
3
β
0
β
1
= α
0
β
0
+
1
2
(α
0
β
1
+ α
1
β
0
)+
1
3
α
1
β
1
.
Next, we use the orthonormal basis found in Example 6.1.9. In this basis G is the
identity matrix and the inner product is the usual one in terms of components.
However, the components of f and g need to be found in {
ˆ
e
1
,
ˆ
e
2
}. The reader may
check that
f = α
0
+ α
1
t = α
0
ˆ
e
1
+ α
1
1
2
√
3
ˆ
e
2
+
1
2
ˆ
e
1
=(α
0
+
1
2
α
1
)
ˆ
e
1
+
α
1
2
√
3
ˆ
e
2
,
g = β
0
+ β
1
t =(β
0
+
1
2
β
1
)
ˆ
e
1
+
β
1
2
√
3
ˆ
e
2
.
It then follows that
f ·g =(α
0
+
1
2
α
1
)(β
0
+
1
2
β
1
)+
α
1
2
√
3
β
1
2
√
3
= α
0
β
0
+
1
2
(α
0
β
1
+ α
1
β
0
)+
1
3
α
1
β
1
.

190 Planar and Spatial Vectors
Finally, we take the dot product of the two vectors using the definition of this dot
product:
f · g =
#
1
0
(α
0
+ α
1
t)(β
0
+ β
1
t) dt
= α
0
β
0
#
1
0
dt +(α
0
β
1
+ α
1
β
0
)
#
1
0
tdt+ α
1
β
1
#
1
0
t
2
dt
= α
0
β
0
+
1
2
(α
0
β
1
+ α
1
β
0
)+
1
3
α
1
β
1
.
All three ways of calculating the inner product agree, as they should.
6.1.3 Orthogonal Transformation
Now that we have defined inner products, we may combine it with the concept
of transformation. More specifically, we seek transformations that leave the
inner product—which we shall assume to be positive definite (Euclidean)—
unchanged. Under such transformations, the length of a vector and the angle
between two vectors will not change. That is why such transformations are
rigid
transformations
called rigid transformations. We choose an orthonormal basis, so that
G = 1, and denote the transformed vectors by a prime: a
= Aa, b
= Ab.
Then the invariance of the inner product yields
8
a
b
=
8
ab ⇒
:
(Aa)Ab =
8
a
8
AAb =
8
ab.
This will hold for arbitrary a and b only if
8
AA = 1. (6.20)
Matrices that satisfy this relation are called orthogonal. We now investigate
orthogonal
matrices
conditions under which Equation (6.20) holds by writing out the matrices:
a
11
a
21
a
12
a
22
a
11
a
12
a
21
a
22
=
a
2
11
+ a
2
21
a
11
a
12
+ a
21
a
22
a
12
a
11
+ a
22
a
21
a
2
12
+ a
2
22
=
10
01
which is equivalent to the following three equations:
a
2
11
+ a
2
21
=1,a
11
a
12
+ a
21
a
22
=0,a
2
12
+ a
2
22
=1. (6.21)
Squaring the second equation and substituting from the first and third, we
get
a
2
11
a
2
12
= a
2
21
a
2
22
⇒ (1 −a
2
21
)a
2
12
= a
2
21
(1 −a
2
12
) ⇒ a
2
21
= a
2
12
.
The first and third equations of (6.21) now yield
a
2
22
= a
2
11
and a
2
12
= a
2
21
=1− a
2
11
.

6.1 Vectors in a Plane Revisited 191
Therefore, all parametersaregivenintermsofa
11
.Nowthefirstequation 2 × 2 orthogonal
matrices are
describedinterms
of a single
parameter.
of (6.21) indicates that −1 ≤ a
11
≤ 1. It follows that a
11
can be thought
of as a sine or a cosine of some angle, say θ. Let us choose cosine. Then
a
22
= ±cos θ. If we choose the plus sign for cosine, then the middle equation
of (6.21) shows that a
12
= −a
21
= ±sin θ, and if we choose the minus sign,
a
12
= a
21
= ±sin θ. Let us choose the plus sign for cosine. Then, we obtain
two possibilities for A:
A =
cos θ −sin θ
sin θ cos θ
or A =
cos θ sin θ
−sin θ cos θ
.
The difference is in the sign of the angle θ.
Writing (x, y) for the components of a vector in the plane [instead of
(α
1
,α
2
)], and (x
,y
) for the transformed vector, and using the first choice for
A,wehave
x
y
=
cos θ −sin θ
sin θ cos θ
x
y
or
x
= x cos θ − y sin θ, (6.22)
y
= x sin θ + y cos θ. (6.23)
This is how the coordinates of a point in the plane transform under a counter-
clockwise rotation of angle θ. Had we chosen the second form of A,wewould
have obtained a clockwise rotation of the coordinates. Notice how we chose
the signs of sines and cosines to ensure that when θ = 0, the rotation is the
unit matrix, i.e., no rotation at all. Although rotations are part of orthogonal
transformations, the converse is not true: There are orthogonal transforma-
tions that do not correspond to a rotation. For example, the matrix
A =
cos θ sin θ
sin θ −cos θ
(6.24)
is orthogonal (as the reader can verify), but it does not correspond to a rota-
tion because at θ = 0 it does not give the identity matrix.
In general, the inner product of the transformed (primed) vectors will be
8
a
Gb
=
:
(Aa)GAb =
8
a
8
AGAb.
For A to preserve the inner product, i.e., for
8
a
Gb
to be equal to
8
aGb, we need
to have
G-orthogonal
matrices
8
AGA = G. (6.25)
A matrix that satisfies Equation (6.25) is called G-orthogonal.
Historical Notes
Matrices entered mathematics slowly and somewhat reluctantly. The related notion
of determinant, which is a number associated with an array of numbers, was intro-
duced as early as the middle of the eighteenth century in the study of a system of

192 Planar and Spatial Vectors
linear equations. However, the recognition that the array itself could be treated as
a mathematical object, obeying certain rules of manipulation, came much later.
Logically, the idea of a matrix precedes that of a determinant as Arthur Cayley
has pointed out; however, the order was reversed historically. In fact, many of the
properties of matrices were known as a result of their connection to determinants.
Because the uses of matrices were well established, it occurred to Cayley to introduce
them as distinct entities. He says, “I certainly did not get the notion of a matrix in
any way through quaternions; it was either directly from that of a determinant or
as a convenient way of expression of” a system of two equations in two unknowns.
Because Cayley was the first to single out the matrix itself and was the first to
publish a series of articles on them, he is generally credited with being the creator
of the theory of matrices.
Arthur Cayley
1821–1895
Arthur Cayley’s father, Henry Cayley, although from a family who had lived
for many generations in Yorkshire, England, lived in St. Petersburg, Russia. It was
in St. Petersburg that Arthur spent the first eight years of his childhood before his
parents returned to England and settled near London. Arthur showed great skill
in numerical calculations at school and, after he moved to King’s College in 1835,
his aptitude for advanced mathematics became apparent. His mathematics teacher
advised that Arthur be encouraged to pursue his studies in this area rather than
follow his father’s wishes to enter the family business as a merchant.
In 1838 Arthur began his studies at Trinity College, Cambridge, from where he
graduated in 1842. While still an undergraduate he had three papers published in
the newly founded Cambridge Mathematical Journal. For four years he taught at
Cambridge having won a Fellowship and, during this period, he published 28 papers.
A Cambridge Fellowship had a limited tenure so Cayley had to find a profession.
He chose law and was admitted to the bar in 1849. He spent 14 years as a lawyer but
Cayley, although very skilled in conveyancing (his legal speciality), always considered
it as a means to make money so that he could pursue mathematics. During this
period he met Sylvester who was also in the legal profession. Both worked at the
courts of Lincoln’s Inn in London and discussed deep mathematical questions during
their working day. During these 14 years as a lawyer Cayley published about 250
mathematical papers!
In 1863 Cayley was appointed to the newly created Sadleirian professorship of
mathematics at Cambridge. Except for the year 1882, spent at the Johns Hopkins
University at the invitation of Sylvester, he remained at Cambridge until his death
in 1895.
6.2 Vectors in Space
The ideas developed so far can be easily generalized to vectors in space. For
example, a linear combination of vectors in space is again a vector in space.
We can also find a basis for space. In fact, any three non-coplanar (not lying
in the same plane) vectors constitute a basis. To see this, let {a
1
, a
2
, a
3
} be
three such vectors drawn from a common point
5
and assume that b is any
fourth vector in space. If b is along any of the a’s, we are done, because then
b is a multiple of that vector, i.e., a linear combination of the three vectors
5
If the vectors are not originally drawn from the same point, we can transport them
parallel to themselves to a common point.
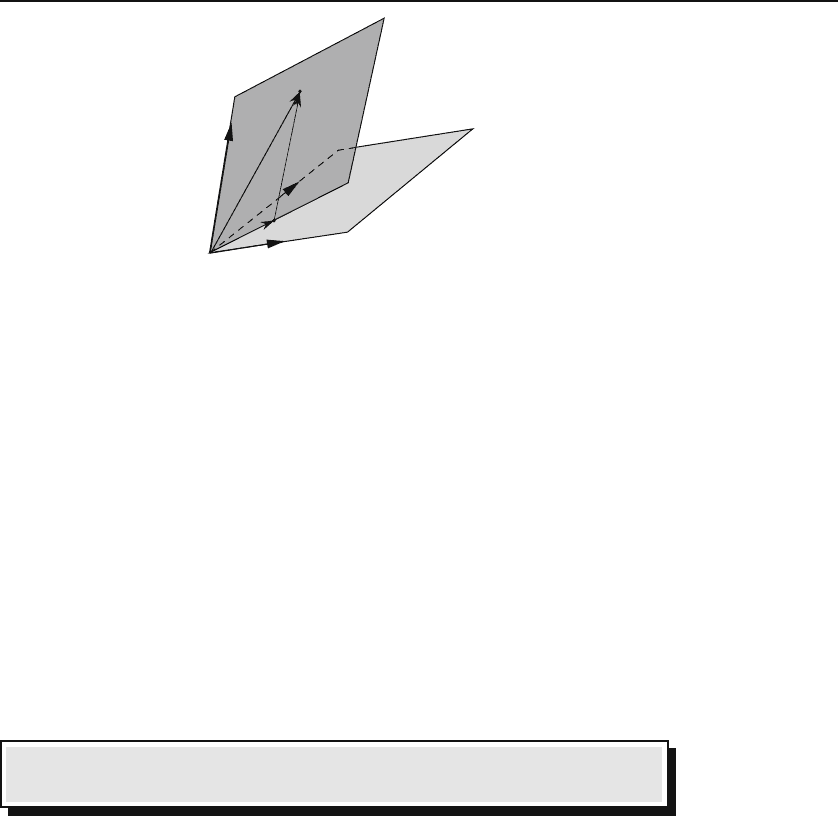
6.2 Vectors in Space 193
b
a
1
a
2
O
B
P
a
3
Figure 6.5: Any vector in space can be written as a linear combination of three non-
coplanar vectors.
(with two coefficients being zero). So assume that b is not along any of the
a’s. The plane formed by b and a
3
intersects the plane of a
1
and a
2
along
a certain line common to both (see Figure 6.5). Draw a line from the tip of
b parallel to a
3
. This line will resolve b intoavector
−−→
OB in the plane of
a
1
and a
2
and a vector
−−→
BP parallel to a
3
.So,wewriteb =
−−→
OB + α
3
a
3
.
Furthermore, since
−−→
OB is in the plane of a
1
and a
2
, it can be written as a
linear combination of these two vectors:
−−→
OB = α
1
a
1
+ α
2
a
2
. Putting all of
this together, we get
b = α
1
a
1
+ α
2
a
2
+ α
3
a
3
.
This shows that
Box 6.2.1. The maximum number of linearly independent vectors in space
is three. Any three non-coplanar vectors form a basis for the space.
It follows that the space is a three-dimensional vector space.
In the previous section we introduced P
1
[t], the set of polynomials of first polynomials of
degree 2 or less
form a
3-dimensional
vector space.
degree, and showed that they could be treated as vectors. We even defined
an inner product for these vectors, and from that, we calculated the length of
a vector and the angle between two vectors. This process can be generalized
to three dimensions. Let P
2
[t] be the set of polynomials of degree 2 (or less)
in the variable t. One can easily show that such a set, a typical element of
which looks like α
0
+ α
1
t + α
2
t
2
, has all the properties of arrows in space. We
shall use P
2
[t] as a prototype of vectors that are not directed line segments.
Clearly, { 1,t,t
2
} form a basis for P
2
[t]; therefore, P
2
[t] is a three-dimensional
vector space.
