Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

5.1 One-Variable Case 143
One can think of the last equality as an identity satisfied by the Dirac delta
function:
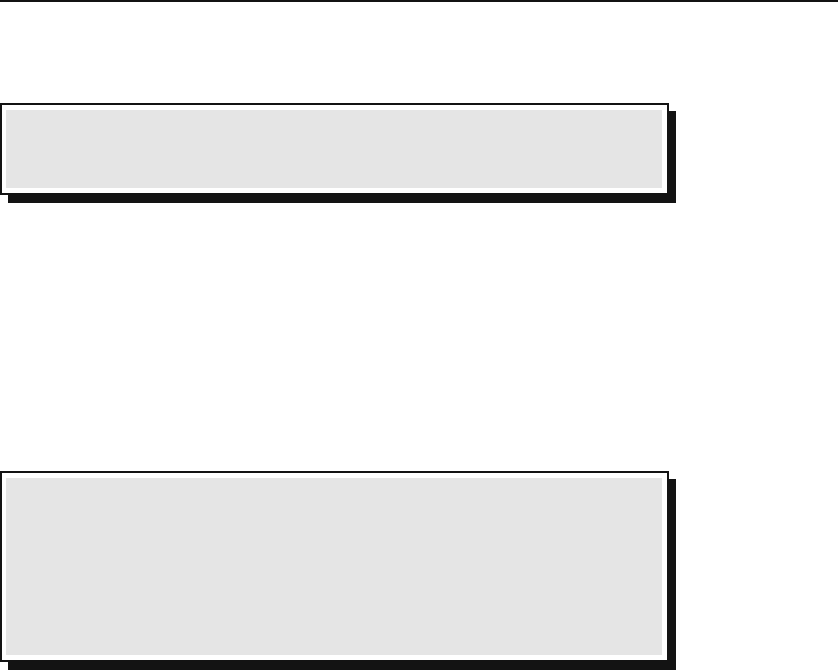
Box 5.1.2. The Dirac delta function is zero everywhere except at the point
which makes its argument zero, in which case the Dirac delta function is
infinite.
Since the Dirac delta function is zero almost everywhere, we can shrink
the region of integration to a smaller interval. In fact,
#
b
a
δ(x −x
0
) dx =1
as long as x
0
lies in the interval (a, b). If x
0
is outside the interval, then the
integral will be zero because the delta function would always be zero in the
region of integration. We summarize these results:
Box 5.1.3. The Dirac delta function satisfies the following relation
#
b
a
δ(x −x
0
) dx =
0
1 if a<x
0
<b,
0 otherwise.
(5.7)
Equation (5.4) is a special case of this, because −∞ <x
0
< +∞ for any
value of x
0
.
5.1.1 Linear Densities of Points
Any function λ(x) whose integral over all real numbers is one is called a linear
density function.Theδ
n
’s defined above are such functions. If we multiply linear density
function
a linear density function by a physical quantity Q, the result will be a linear
density for Q. In fact, this was how we arrived at δ
n
.Thus,Q
0
λ(x)isa
Q-linear density with total magnitude Q
0
. Similarly, if M represents a mass,
then Mλ(x) is a linear mass density with total mass M .Conversely,iff(x)
describes the linear density of a physical quantity with total magnitude Q,
then λ(x) ≡ f(x)/Q is a linear density function.
Because of Equation (5.4) the Dirac delta function is a linear density func-
tion. What kind of a distribution does it describe? To be specific, consider
δ function and
densities of point
charges and point
masses
mδ(x, x
0
)withm designating mass. This function is zero everywhere except
at x
0
. Thus, if it is to be a mass distribution, it has to be a point mass located
at x
0
. Keep in mind that mδ(x, x
0
) is a linear mass density,sothatitsintegral
is the total mass m. The linear “density” of a point mass is infinite because

144 Dirac Delta Function
its length is zero, and this is precisely what mδ(x, x
0
) describes. In fact, the
linear density of a point physical quantity of magnitude Q located at x
0
can
be written as Qδ(x, x
0
)=Qδ(x −x
0
), or generalizing,
Box 5.1.4. The linear density λ(x) of N point physical quantities
Q
1
,Q
2
,...,Q
N
located at x
1
,x
2
,...,x
N
, respectively, can be written as
λ(x)=
N
k=1
Q
k
δ(x −x
k
). (5.8)
We see that with the help of the Dirac delta function we can express discrete
charge distributions (collection of point charges) in terms of functions. This
is the most useful property of the Dirac delta function.
Example 5.1.1.
Three charges −q,2q,and−q are located along the x-axis at
−a, the origin, and +a, respectively. How do we write the linear charge density for
such a charge distribution? We use Equation (5.8) with Q replaced by q:
λ(x)=
3
k=1
q
k
δ(x − x
k
)=−qδ(x − (−a)) + 2qδ(x − 0) − qδ(x − a)
= −qδ(x + a)+2qδ(x) − qδ(x − a).
Note that the Dirac delta functions ensure that no electric charge is present any
where except at x = a, x = −a,andx =0.
Example 5.1.2. A more interesting example of a linear charge distribution using
the Dirac delta function is that of an infinite array of point charges equally spaced
on a straight line having equal magnitudes and alternating in sign. This is a one-
dimensional model of ionic crystals.
Let us assume that the magnitude of each charge is ±q, the spacing between it
and the neighboring charge is a, and that the charges start at −∞ and extend to
+∞ with one positive charge at the origin as shown in Figure 5.4. Then it is easy
to write the density of this distribution. It isdensity of
one-dimensional
ionic crystal
λ(x)=
+∞
k=−∞
(−1)
k
qδ(x − ka).
a
O
Figure 5.4: A one-dimensional ionic crystal. The black circles represent positive charges
and the white circles the negative charges.

5.1 One-Variable Case 145
Note that for odd k thechargeisnegativeandforevenk it is positive. This is
because we placed a positive charge at the origin. Had we chosen the origin to
be the site of a negative charge, the above arrangement would have shifted by one
spacing.
5.1.2 Properties of the Delta Function
From a mathematical point of view, the most important property, which is
sometimes used to define the Dirac delta function, occurs when it multiplies a
“smooth”
1
function in an integrand. First look at an integral with a δ
n
(x−x
0
)
inside. If the function f (x) multiplying δ
n
(x − x
0
)issmoothandn is large
enough, the product f(x)δ
n
(x − x
0
) practically vanishes outside a narrow
interval in which δ
n
(x − x
0
) is appreciably different from zero. For example,
if n =10
7
, x = x
0
+0.001, and we use the exponential function of Equation
(5.1), then δ
n
(x − x
0
)=0.08, so that f (x)δ
n
(x − x
0
) drops to about 8% of
the value it has at x
0
, assuming that f does not change appreciably in the
small interval of width 0.002 around x
0
. For larger values of n this drop is
even sharper. In fact, no matter what function we choose, there is always a
large enough n such that the product f (x)δ
n
(x − x
0
) will drop to as small
a value as we please in as short an interval as we please. Therefore, we can
approximate the integral over all real numbers to an integral over that small
interval. Let the interval be (x
0
− , x
0
+ ). Then, we have
#
+∞
−∞
f(x)δ
n
(x − x
0
) dx ≈
#
x
0
+
x
0
−
f(x)δ
n
(x − x
0
) dx
≈ f (x
0
)
#
x
0
+
x
0
−
δ
n
(x − x
0
) dx
≈ f (x
0
)
#
+∞
−∞
δ
n
(x −x
0
)=f(x
0
).
The approximation in the second line follows from the fact that f (x)isalmost
constant in the small interval (x
0
− , x
0
+ ). The third approximation is a
result of the smallness of δ
n
outside the interval, and the equality follows
because δ
n
is a linear density function. The approximation above reaches
equality once the limit of n →∞is taken in which case δ
n
becomes the Dirac
delta function. Thus, we have the important relation
#
+∞
−∞
f(x)δ(x − x
0
) dx = f(x
0
). (5.9)
1
In the present context, a smooth function is one that does not change abruptly when
its argument changes by a small amount.

146 Dirac Delta Function
This is equivalent to the following statement:integral of product
of δ(x − x
0
) and
f(x) is simply
f(x
0
)
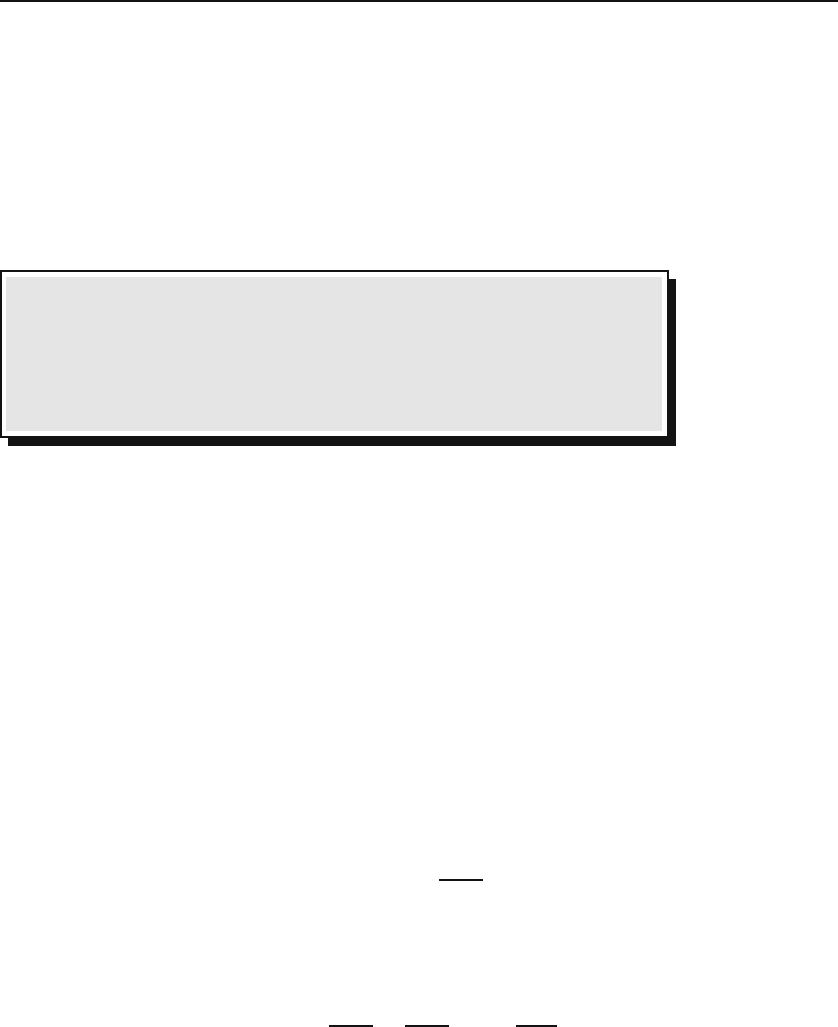
Box 5.1.5. The Dirac delta function satisfies
#
b
a
f(x)δ(x − x
0
) dx =
0
f(x
0
) if a<x
0
<b,
0 otherwise.
(5.10)
In words, the result of integration is the value of f at the root of the
argument of the delta function, provided this root is inside the range
of integration.
Example 5.1.3. In this example we illustrate some of the properties of the
Dirac delta function. For instance
∞
1
f(t)δ(t) dt = 0 because the root of the
argument of the Dirac delta function (the point that makes the argument of the
Dirac delta function zero)—namely t = 0—is outside the range of integration. The
integral
+∞
−∞
xδ(x) dx is zero because the function x vanishes at the point x = 0 (the
root of the argument of the delta function). Also,
#
+3
−∞
cos yδ(y −π) dy =0
because π—which makes the argument of the delta function vanish—lies outside the
range of integration. However,
#
+3.2
−∞
cos yδ(y − π) dy =cosπ = −1
because now π lies inside the range of integration.
The reader is urged to check the following results:
#
+∞
−∞
cos yδ(y −π) dy = −1,
#
+∞
−∞
sin zδ(z) dz =0,
#
+∞
0
cos yδ(y + π) dy =0,
#
+∞
−∞
cos
y
2
δ(y − π) dy =0,
#
1
−1
e
t
δ(t) dt =1,
#
+∞
−∞
xf(x)δ(x) dx =0,
#
2.7
−∞
ln tδ(t −e) dt =0,
#
2.8
−∞
ln tδ(t − e) dt =1.
As noted earlier, the Dirac delta function is not an ordinary over-the-
counter function. Nevertheless, it is possible to study it, along with many
other “weird” functions called distributions, in a mathematically rigorous
distributions
and systematic way. It turns out that, in all physical applications, distribu-
tions occur inside an integral, and once they do, Equation (5.10) tells us how
to manipulate such integrals. The result of integration is always well defined
because it is simply the value of a “good” function at a point, say x
0
.Infact,
5.1 One-Variable Case 147
the result of integration is so nice that one can even define the derivative of
the Dirac delta function by differentiating (5.10) with respect to x
0
.Weleave
the details as an exercise and simply quote the result:
#
+∞
−∞
f(x)δ
(x − x
0
) dx = −f
(x
0
) (5.11)
Higher order derivatives of the Dirac delta function can be obtained similarly.
derivatives of
Dirac delta
function
In fact, we have
Box 5.1.6. The nth derivative of the Dirac delta function satisfies
#
b
a
f(x)δ
(n)
(x−x
0
)(x−x
0
) dx =
0
(−1)
n
f
(n)
(x
0
) if a<x
0
<b,
0 otherwise,
(5.12)
where the superscript (n) indicates the nth derivatives.
In many applications the argument of the Dirac delta function is not of
the simple form (x − x
0
), but may itself be a function g(x) whose deriva-
tive is assumed to be continuous in (a, b). Since by Equation (5.6) the delta
what happens
when the
argument of δ is
itself a function?
function vanishes except when its argument is zero, in such a case, one has
to concentrate on the roots of g(x), i.e., values c for which g(c)=0. For
simplicity, first assume that there is only one root c of g in the interval (a, b)
and that g
(c) > 0. Then, since the Dirac delta function is zero everywhere
in the interval (a, b), except at x = c,wecanshrinktheregionofintegration
to (c −, c + ), and write
#
b
a
δ (g(x)) dx =
#
c+
c−
δ (g(x)) dx.
Now make the change of variable y = g(x), dy = g
(x) dx with the appropriate
transformation of limits of integration to get
#
b
a
δ (g(x)) dx =
#
g(c+)
g(c− )
δ(y)
dy
g
(x)
.
With g(c)=0andg
(c) > 0, we conclude that g is increasing in the interval
(c −, c + ), that g(c −) < 0, and that g(c + ) > 0. We can therefore write
#
b
a
δ (g(x)) dx =
#
g(c+)
g(c− )
δ(y)
dy
g
(x)
=
1
g
(x)
y=0
=
1
g
(c)
> 0,
because zero is in the region of integration and y = 0 is equivalent to x = c
there.

148 Dirac Delta Function
When g
(c) < 0, g will be decreasing in the interval (c − , c + ), and
g(c − ) > 0andg(c + ) < 0. Thus, flipping the limits of integration so that
the smaller number corresponds to the lower limit, we obtain
#
b
a
δ (g(x)) dx = −
#
g(c− )
g(c+)
δ(y)
dy
g
(x)
= −
1
g
(x)
y=0
= −
1
g
(c)
> 0.
We summarize the two results as
#
b
a
δ (g(x)) dx =
1
|g
(c)|
.
If there are two roots of g in the interval, say c
1
and c
2
with c
2
>c
1
,we
break up (a, b):
#
b
a
δ (g(x)) dx =
0
#
c
1
−
a
δ (g(x)) dx +
#
c
1
+
c
1
−
δ (g(x)) dx
+
0
#
c
2
−
c
1
+
δ (g(x)) dx +
#
c
2
+
c
2
−
δ (g(x)) dx
+
0
#
b
c
2
+
δ (g(x)) dx =
1
|g
(c
1
)|
+
1
|g
(c
2
)|
,
where in the last line we used the result obtained in the previous paragraph.
It should be clear that if g has n roots c
1
,c
2
,...,c
n
in (a, b), there will be a
summation of n terms in the last line of the above equation. In fact, we can
summarize the result of the foregoing discussion as
Box 5.1.7. If g(x) has the roots c
1
,c
2
,...,c
n
,andg
(c
k
) =0for all k
between 1 and n,then
#
b
a
δ(g(x)) dx =
0
n
k=1
1/|g
(c
k
)| if a<c
k
<b,
0 otherwise.
(5.13)
When the delta function is multiplied by a smooth function f (x), a similar
argument as above—which is left to the reader—can be used to show that
#
b
a
f(x)δ(g(x)) dx =
0
n
k=1
f(c
k
)/|g
(c
k
)| if a<c
k
<b,
0otherwise,
(5.14)

5.1 One-Variable Case 149
provided g
(c
k
) = 0. These results are sometimes written as an identity among
the delta functions.
a very important
relation
Box 5.1.8. The Dirac delta function satisfies the following relation:
δ(g(x)) =
n
k=1
δ(x −c
k
)
|g
(c
k
)|
,g
(c
k
) =0, (5.15)
where {c
k
}
n
k=1
are all the roots of the equation g(x)=0.
The formula analogous to Equation (5.14) involving the derivative of the Dirac
delta function is
#
b
a
f(x)δ
(g(x)) dx =
0
−
n
k=1
f
(c
k
)/|g
(c
k
)| if a<c
k
<b,
0otherwise.
(5.16)
Example 5.1.4.
As a concrete example, let us evaluate the integral
I ≡
#
+∞
−∞
f(t)δ(t
2
− a
2
) dt,
where f is a smooth function and a is a real constant. We can identify g(t)ast
2
−a
2
with roots c
1
= −a, c
2
= a and derivative g
(t)=2t. Therefore, Equation (5.15)
reduces to
δ(t
2
− a
2
)=
δ(t − c
1
)
|g
(c
1
)|
+
δ(t − c
2
)
|g
(c
2
)|
=
δ(t − (−a))
|−2a|
+
δ(t − a)
|2a|
=
1
|2a|
{δ(t + a)+δ(t − a)}.
Substituting in the integral, we obtain
I =
1
2|a|
#
+∞
−∞
f(t) {δ(t + a)+δ(t − a)}
=
1
2|a|
(
#
+∞
−∞
f(t)δ(t + a)+
#
+∞
−∞
f(t)δ(t − a)
)
=
1
2|a|
{f(−a)+f(a)}.
Note that the integral vanishes—as expected—if f is odd.
Example 5.1.5. We illustrate further the foregoing general discussions with some
more concrete examples. To evaluate the integral
#
∞
1
sin tδ(t
2
− π
2
/4) dt,

150 Dirac Delta Function
we note that g(t)=t
2
− π
2
/4 which has two roots c
1
= π/2andc
2
= −π/2with
only the positive root lying in the range of integration. Moreover, g
(t)=2t.Thus,
#
∞
1
sin tδ(t
2
− π
2
/4) dt =
f(c
1
)
|g
(c
1
)|
=
sin(c
1
)
|2c
1
|
=
sin(π/2)
π
=
1
π
.
On the other hand,
#
∞
−∞
sin tδ(t
2
− π
2
/4) dt =0
because the second root c
2
is also included in the range of integration and its con-
tribution cancels that of c
1
.
To evaluate the integral
#
∞
0
ln zδ(z
2
− 4) dz
we note that g(z)=z
2
− 4 which has two roots c
1
=2andc
2
= −2 with only the
positive root lying in the range of integration. Thus, with g
(z)=2z,wehave
#
∞
0
ln zδ(z
2
− 4) dz =
f(c
1
)
|g
(c
1
)|
=
ln(c
1
)
|2c
1
|
=
ln 2
4
=0.1733.
The integral
#
+∞
−∞
f(y) δ(y
2
+ a
2
) dy
is zero because there is no point in the range of integration at which the argument
of the Dirac delta function vanishes. In other words, g(y)=y
2
+ a
2
has no real
roots at all.
To evaluate the integral
#
+π/2
−π/2
(t +1)
2
δ(sin πt) dt
we note that g(t)=sinπt which has three roots c
1
= −1, c
2
=0,andc
3
=+1in
the range of integration. Thus, with g
(t)=π cos πt,wehave
#
+π/2
−π/2
(t +1)
2
δ(sin πt) dt =
3
k=1
f(c
k
)
|g
(c
k
)|
=
3
k=1
(c
k
+1)
2
|π cos(c
k
π)|
=
(−1+1)
2
|π cos(−π)|
+
(0 + 1)
2
|π cos(0)|
+
(1 + 1)
2
|π cos(π)|
=
5
π
.
Some other concrete examples are:
#
+∞
−∞
sin |t| δ(t
2
− π
2
/4) dt =2/π,
#
+∞
−∞
cos xδ(x
2
− π
2
) dx = −1/π,
#
∞
0
ln zδ(z
2
− 1) dz =0,
#
+3
−∞
cos yδ(y
2
+ π
2
) dy =0,
#
+π
−π
(t +1)
2
δ(sin πt) dt =35/π,
#
+∞
−∞
f(t) δ(e
t
− 1) dt = f(0),
#
∞
0
ln xδ(10x
2
+3x −1) dx = −0.23,
#
+∞
−∞
f(t) δ(e
t
) dt =0.
The reader is urged to derive all the above relations.

5.1 One-Variable Case 151
Historical Notes
“Physical laws should have mathematical beauty.” This statement was Dirac’s re-
sponse to the question of his philosophy of physics, posed to him in Moscow in 1955.
He wrote it on a blackboard that is still preserved today.
Paul Adrien Maurice Dirac (1902–1984), was born in 1902 in Bristol, Eng-
land, of a Swiss, French-speaking father and an English mother. His father, a
taciturn man who refused to receive friends at home, enforced young Paul’s silence
by requiring that only French be spoken at the dinner table. Perhaps this explains
Dirac’s later disinclination toward collaboration and his general tendency to be a
loner in most aspects of his life. The fundamental nature of his work made the
involvement of students difficult, so perhaps Dirac’s personality was well-suited to
his extraordinary accomplishments.
Dirac went to Merchant Venturer’s School, the public school where his father
taught French, and while there displayed great mathematical abilities. Upon grad-
uation, he followed in his older brother’s footsteps and went to Bristol University to
study electrical engineering. He was 19 when he graduated from Bristol University
in 1921. Unable to find a suitable engineering position due to the economic reces- “The amount of
theoretical ground
one has to cover
before being able
to solve problems
of real practical
value is rather
large, but this
circumstance is an
inevitable
consequence of
the fundamental
part played by
transformation
theory and is likely
to become more
pronounced in the
theoretical physics
of the future.”
P.A.M. Dirac
(1930)
sion that gripped post-World War I England, Dirac accepted a fellowship to study
mathematics at Bristol University. This fellowship, together with a grant from the
Department of Scientific and Industrial Research, made it possible for Dirac to go
to Cambridge as a research student in 1923. At Cambridge Dirac was exposed to
the experimental activities of the Cavendish Laboratory, and he became a member
of the intellectual circle over which Rutherford and Fowler presided. He took his
PhD in 1926 and was elected in 1927 as a fellow. His appointment as university
lecturer came in 1929. He assumed the Lucasian professorship following Joseph
Larmor in 1932 and retired from it in 1969. Two years later he accepted a position
at Florida State University where he lived out his remaining years. The FSU library
now carries his name.
In the late 1920s the relentless march of ideas and discoveries had carried physics
to a generally accepted relativistic theory of the electron. Dirac, however, was dis-
satisfied with the prevailing ideas and, somewhat in isolation, sought for a better
formulation. By 1928 he succeeded in finding an equation, the Dirac equation,that
accorded with his own ideas and also fitted most of the established principles of the
time. Ultimately, this equation, and the physical theory behind it, proved to be
one of the great intellectual achievements of the period. It was particularly remark-
able for the internal beauty of its mathematical structure, which not only clarified
previously mysterious phenomena such as spin and the Fermi–Dirac statistics
associated with it, but also predicted the existence of an electron-like particle of
negative energy, the antielectron, or positron, and, more recently, it has come to
play a role of great importance in modern mathematics, particularly in the inter-
relations between topology, geometry, and analysis. Heisenberg characterized the
discovery of antimatter by Dirac as “the most decisive discovery in connection with
the properties or the nature of elementary particles . . . . This discovery of particles
and antiparticles by Dirac ...changed our whole outlook on atomic physics com-
pletely.” One of the interesting implications of his work that predicted the positron
Paul Adrien
Maurice Dirac
1902–1984
was the prediction of a magnetic monopole. Dirac won the Nobel Prize in 1933 for
this work.
Dirac is not only one of the chief authors of quantum mechanics, but he is
also the creator of quantum electrodynamics and one of the principal architects of

152 Dirac Delta Function
quantum field theory. While studying the scattering theory of quantum particles, he
invented the (Dirac) delta function; in his attempt at quantizing the general theory
of relativity, he founded constrained Hamiltonian dynamics, which is one of the most
active areas of theoretical physics research today. One of his greatest contributions
is the invention of the bra | and ket | notation used in quantum theory.
While at Cambridge, Dirac did not accept many research students. Those who
worked with him generally thought that he was a good supervisor, but one who
did not spend much time with his students. A student needed to be extremely
independent to work under Dirac. One such student was Dennis Sciama,wholater
became the supervisor of Stephen Hawking, the current holder of the Lucasian chair.
Salam and Wigner in their Preface to the Festschrift that honors Dirac on his
seventieth birthday and commemorates his contributions to quantum mechanics
succinctly assessed the man:
Dirac is one of the chief creators of quantum mechanics.... Posterity
will rate Dirac as one of the greatest physicists of all time. The present
generation values him as one of its greatest teachers.... On those privi-
leged to know him, Dirac has left his mark ...by his human greatness.
He is modest, affectionate, and sets the highest possible standards of
personal and scientific integrity. He is a legend in his own lifetime and
rightly so.
(Taken from Schweber, S. S. “Some chapters for a history of quantum field theory:
1938–1952,” in Relativity, Groups, and Topology II,vol. 2,B.S.DeWittandR.
Stora, eds., North-Holland, Amsterdam, 1984.)
5.1.3 The Step Function
The step function θ is defined as
θ(x)=
0
1ifx>0
0ifx<0
(5.17)
The θ function (as it is often called) is useful in writing functions that have
discontinuities or cusps. For instance, absolute values can be written in terms
of the step function:
|x| = xθ(x) − xθ(−x)or|x − y| =(x − y)[θ(x −y) −θ(y − x)]
A piecewise continuous function such as
g(x)=
0
g
1
(x)if0<x<1
g
2
(x)ifx>1
(5.18)
can be written as
g(x)=g
1
(x)θ(x)θ(1 − x)+g
2
(x)θ(x − 1)
