Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


112 Integration: Applications
Cartesian Coordinates
To obtain the magnetic field we substitute
r = x
ˆ
e
x
+ y
ˆ
e
y
+ z
ˆ
e
z
,
r
= x
ˆ
e
x
+ y
ˆ
e
y
+ z
ˆ
e
z
,
dr
=
ˆ
e
x
dx
+
ˆ
e
y
dy
+
ˆ
e
z
dz
,
r − r
=
x − x
!
ˆ
e
x
+
y − y
!
ˆ
e
y
+
z − z
!
ˆ
e
z
,
|r − r
|
3
=
*
x − x
!
2
+
y − y
!
2
+
z − z
!
2
+
3/2
in Equation (4.18). For the cross product, we need to expand the determinant
dr
× (r − r
)=det
⎛
⎝
ˆ
e
x
ˆ
e
y
ˆ
e
z
dx
dy
dz
x − x
y − y
z − z
⎞
⎠
,
using Figure 1.5.
Cylindrical Coordinates
The cylindrical coordinates can be handled in exact analogy with the Carte-
sian case. Using Equations (1.19) and (2.28), we have
r = ρ
ˆ
e
ρ
+ z
ˆ
e
z
, r
= ρ
ˆ
e
ρ
+ z
ˆ
e
z
,
r − r
= ρ
ˆ
e
ρ
− ρ
ˆ
e
ρ
+(z − z
)
ˆ
e
z
, (4.19)
dr
=
ˆ
e
ρ
dρ
+
ˆ
e
ϕ
ρ
dϕ
+
ˆ
e
z
dz
,
|r − r
|
3
=
,
ρ
2
+ ρ
2
− 2ρρ
cos(ϕ − ϕ
)+(z − z
)
2
-
3/2
.
The cross product cannot be done using determinants because not everything
is written in terms of the three mutually perpendicular unit vectors:
ˆ
e
ρ
is
different from
ˆ
e
ρ
but not perpendicular to it. In fact, this difference is the
cause for the appearance of the cosine term in the last equation of (4.19). To
find the cross product, we simply multiply the two terms and use the following
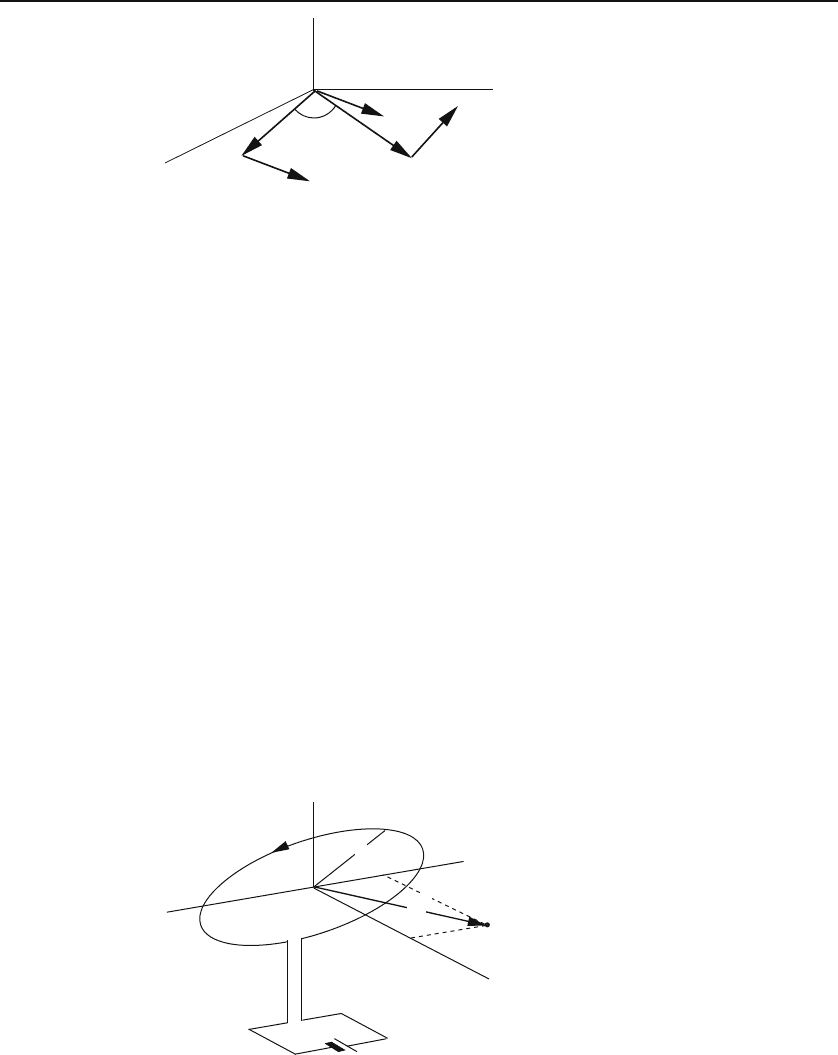
relations, most of which should be familiar, and the unfamiliar ones can be
obtained using Figure 4.7:
ˆ
e
ρ
×
ˆ
e
ρ
=
ˆ
e
z
sin(ϕ − ϕ
),
ˆ
e
ρ
×
ˆ
e
z
= −
ˆ
e
ϕ
,
ˆ
e
ϕ
×
ˆ
e
ρ
= −
ˆ
e
z
cos(ϕ − ϕ
),
ˆ
e
ϕ
×
ˆ
e
ρ
= −
ˆ
e
z
,
ˆ
e
ϕ
×
ˆ
e
z
=
ˆ
e
ρ
,
ˆ
e
z
×
ˆ
e
ρ
=
ˆ
e
ϕ
, (4.20)
ˆ
e
z
×
ˆ
e
ρ
=
ˆ
e
ϕ
.
The cross product can be written as
dr
× (r − r
)=
ˆ
e
z
.
ρ
2
dϕ
+ ρ sin(ϕ − ϕ
) dρ
− ρρ
cos(ϕ − ϕ
) dϕ
/
−
ˆ
e
ϕ
.
(z − z
) dρ
+ ρ
dz
/
(4.21)
+
ˆ
e
ϕ
ρdz
+
ˆ
e
ρ
ρ
(z − z
) dϕ
.
4.1 Single Integrals 113
z
x
y
e
^
ρ
e
^
e
^
ϕ
e
^
e
^
ρ
'
ϕ
'
ϕ
'
ϕ
−
ϕ
'
Figure 4.7: The orientation of some of the cylindrical unit vectors drawn for the
calculation of cross products.
To find the components of the magnetic field, we substitute this in
Equation (4.18), take the dot product of cylindrical unit vectors with the
integrand, and use
ˆ
e
ρ
·
ˆ
e
ρ
=cos(ϕ
− ϕ),
ˆ
e
ρ
·
ˆ
e
ϕ
=sin(ϕ
− ϕ),
ˆ
e
ρ
·
ˆ
e
ϕ
= −sin(ϕ
− ϕ),
ˆ
e
ϕ
·
ˆ
e
ϕ
=cos(ϕ
− ϕ), (4.22)
as well as the other more obvious dot products of unit vectors.
We can derive a general expression for the components of the electric field
in terms of the parametric functions of a general curve (see Problem 4.6).
However, a simple example will also illustrate the general procedure without
entangling the formulas with complicated expressions.
Example 4.1.4.
A simple application of the foregoing general formalism is to
calculate the magnetic field of a circular loop of radius a. The choice of the axes
and origin of Figure 4.8 yields the following parameterization of the loop:
ρ
= a, dρ
=0; ϕ
= t, dϕ
= dt; z
=0,dz
=0, 0 ≤ t ≤ 2π.
Furthermore, because of the azimuthal symmetry of the current distribution, the
final answer will be independent of ϕ. Thus, we can set that equal to zero. Inserting
this information in Equations (4.19) and (4.21) gives
x
y
z
I
r
ρ
P
a
z
+
−
Figure 4.8: The geometry of the circular loop of current.

114 Integration: Applications
|r − r
|
3
=
.
ρ
2
+ a
2
− 2ρa cos(t)+z
2
/
3/2
dr
× (r − r
)=
ˆ
e
z
.
a
2
dt − ρa cos(t) dt
/
+
ˆ
e
ρ
az dt.
The magnetic field of Equation (4.18) can now be written as
B = k
m
I
#
2π
0
ˆ
e
z
.
a
2
− ρa cos(t)
/
+
ˆ
e
ρ
az
.
ρ
2
+ a
2
− 2ρa cos(t)+z
2
/
3/2
dt (4.23)
Finally, to find the cylindrical components, dot-multiply (4.23) with the cylin-
drical unit vectors and use Equation (4.22) with ϕ =0(andϕ
= t):
B
ρ
= B ·
ˆ
e
ρ
= k
m
Ia
#
2π
0
*
ˆ
e
z
a − ρ cos t
!
+
ˆ
e
ρ
z
+
·
ˆ
e
ρ
ρ
2
+ a
2
− 2ρa cos t + z
2
!
3/2
dt
= k
m
Ia
#
2π
0
=0
ˆ
e
z
·
ˆ
e
ρ
a − ρ cos t
!
+
=cos t
ˆ
e
ρ
·
ˆ
e
ρ
z
ρ
2
+ a
2
− 2ρa cos t + z
2
!
3/2
dt (4.24)
= k
m
Iaz
#
2π
0
cos tdt
(ρ
2
+ a
2
− 2ρa cos t + z
2
)
3/2
,
Similarly,
B
ϕ
= B ·
ˆ
e
ϕ
= k
m
Ia
#
2π
0
=0
ˆ
e
z
·
ˆ
e
ϕ
a − ρ cos t
!
+
=sin t
ˆ
e
ρ
·
ˆ
e
ϕ
z
ρ
2
+ a
2
− 2ρa cos t + z
2
!
3/2
dt
= k
m
Iaz
#
2π
0
sin tdt
(ρ
2
+ a
2
− 2ρa cos t + z
2
)
3/2
(4.25)
= −
k
m
Iz
ρ
(ρ
2
+ a
2
− 2aρ cos t + z
2
)
−1/2
2π
0
=0,
and
B
z
= B ·
ˆ
e
z
= k
m
Ia
#
2π
0
=1
ˆ
e
z
·
ˆ
e
z
a − ρ cos t
!
+
=0
ˆ
e
ρ
·
ˆ
e
z
z
ρ
2
+ a
2
− 2ρa cos t + z
2
!
3/2
dt
= k
m
Ia
#
2π
0
(a − ρ cos t) dt
(ρ
2
+ a
2
− 2ρa cos t + z
2
)
3/2
. (4.26)
Once again the azimuthal symmetry prohibits a ϕ-component for the field. These
integrals cannot be evaluated analytically, but if we specialize to the case where P
is on the z-axis (i.e., when ρ = 0), the integrals become trivial. In fact, we have
B
ρ
= k
m
Iaz
#
2π
0
cos tdt
(a
2
+ z
2
)
3/2
=0,
B
ϕ
=0,
B
z
= −k
m
Ia
#
2π
0
−adt
(a
2
+ z
2
)
3/2
=
2πk
m
Ia
2
(a
2
+ z
2
)
3/2
.

4.2 Applications: Double Integrals 115
Historical Notes
After graduating from the college of Louis-le-Grand in Paris and subsequently spend-
ing some time in the army, Jean-Baptiste Biot entered the Ecole Polytechnique
in Paris where Monge (a noted mathematician of the time and an expert in dif-
ferential geometry) realized his potential. Because of his political views and his
participation in an attempted insurrection by the royalists against the Convention,
Biot was captured by government forces and taken prisoner. Had it not been for
Jean-Baptiste Biot
1774–1862
Monge’s intervention and plead for his release, Biot’s promising career might have
ended.
Biot became Professor of Mathematics at the Ecole Centrale at Beauvais in
1797, and three years later joined the faculty of the Coll`ege de France as Professor
of Mathematical Physics an appointment which was due to the influence of Laplace.
Biot studied a wide range of mathematical topics, mostly on the applied math-
ematics side. He made advances in astronomy, elasticity, heat, and optics while, in
pure mathematics, he also did important work in geometry. He collaborated with
Arago on the refractive properties of gases.
Biot’s most notable contribution was done in collaboration with Felix Savart
(1791–1841), who was an acoustics expert and developed the Savart disk, a device
which produced a sound wave of known frequency, using a rotating cog wheel as a
measuring device.
Biot and Savart jointly discovered that the intensity of the magnetic field set up
by a current flowing through a wire varies inversely with the distance from the wire.
This is a special case of what is now known as Biot–Savart’s Law and is fundamental
to modern electromagnetic theory.
For his work on the polarization of light passing through chemical solutions Biot
was awarded the Rumford Medal of the Royal Society. He tried twice for the post
of Secretary to the Acad´emie des Sciences but lost out in 1822 to Fourier for this
post. When Fourier died he applied again only to lose to Arago.
4.2 Applications: Double Integrals
Whenever areas are sources of physical quantities such as fields, or interactions
take place on areas, such as pressure applied on a surface, double integrals
are used. We can be as general as in the previous section and consider a gen-
eral surface given by a parametric equation in two variables (instead of one
used for curves). However, since the geometry of surfaces is much more com-
plicated, and much less illuminating, we shall confine our discussion to very
simple geometries which require trivial and obvious parameterization. More
specifically, we restrict ourselves to primary surfaces of the three coordinate
systems.
4.2.1 Cartesian Coordinates
Since we are restricting ourselves to primary surfaces, our choice for Cartesian
coordinates is narrowed down to planes, and if we want the boundaries of the
plane to be simple in Cartesian coordinates, we are limited to just a rectangle.

116 Integration: Applications
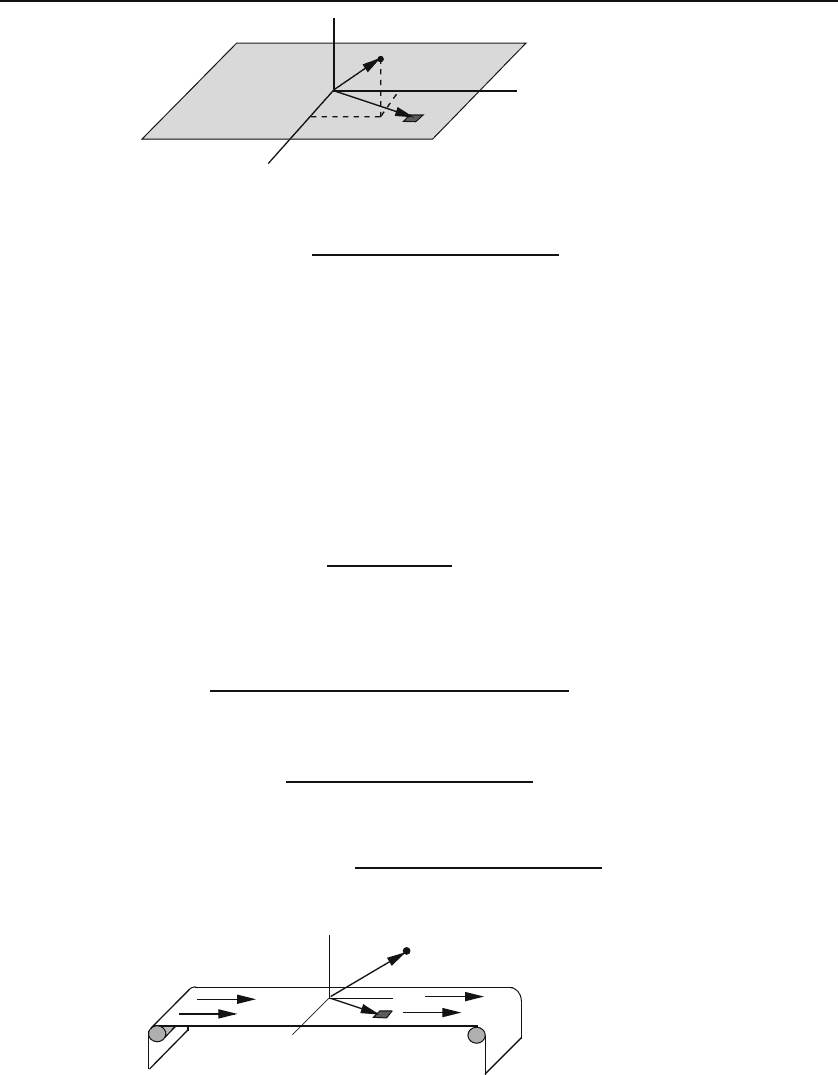
Example 4.2.1. We start with an example from electrostatics. A rectangular flat
surface of sides a and b is charged uniformly with surface charge density σ,andwe
are interested in the electric field at a general point P in space. This is given by
E =
##
Ω
k
e
dq(r
)
|r − r
|
3
(r − r
)
with r = x
ˆ
e
x
+y
ˆ
e
y
+z
ˆ
e
z
= x, y, z and r
= x
ˆ
e
x
+y
ˆ
e
y
= x
,y
, 0, where we have
chosen the plane of the rectangle to be the xy-plane. If we choose the center of the
rectangle to be our origin, our z-axis perpendicular to the plane of the rectangle,
and our x-and y-axes parallel to the sides as shown in Figure 4.9, then the element
of area coincides with the third primary element, and we can write
dq(r
)=σ(r
) da(r
)=σdx
dy
.
We also have
r − r
=(x − x
)
ˆ
e
x
+(y − y
)
ˆ
e
y
+ z
ˆ
e
z
= x − x
,y− y
,z,
|r − r
| =
(x − x
)
2
+(y − y
)
2
+ z
2
,
|r − r
|
3
=
,
(x − x
)
2
+(y − y
)
2
+ z
2
-
3/2
.
Inserting all these relations in the expression for E,weobtain
E =
##
Ω
k
e
σdx
dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
.
(x − x
)
ˆ
e
x
+(y − y
)
ˆ
e
y
+ z
ˆ
e
z
/
with componentselectric field of a
uniformly charged
rectangle
E
x
= k
e
σ
##
Ω
(x − x
) dx
dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
,
E
y
= k
e
σ
##
Ω
(y −y
) dx
dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
,
E
z
= k
e
σz
##
Ω
dx
dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
,
where everything independent of the variables of integration, x
and y
, is taken out
of the integrals.
We have already discussed a general procedure for evaluating multiple integrals
by reducing them to lower-dimensional integrals. We follow the same procedure
here: The y
integration has the lower limit −b/2 and the upper limit +b/2, both
independent of x
.
4
Similarly, the x
integration has −a/2anda/2 as its limits.
This means that the components can be written as
E
x
= k
e
σ
#
a/2
−a/2
(x − x
) dx
#
b/2
−b/2
dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
,
E
y
= k
e
σ
#
a/2
−a/2
dx
#
b/2
−b/2
(y −y
) dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
,
4
The independence of the limits is one reason that Cartesian coordinates are useful for
rectangular regions of integration. If we had chosen cylindrical coordinates, then the limits
of integration, the lines y
= −b/2andy
= b/2, would have had to be written in cylindrical
coordinates, giving, for the upper limit, for example, ρ
sin ϕ
= b/2orρ
= b/(2 sin ϕ
).
Thus a ρ
integration with limits dependent on ϕ
would have been involved.
4.2 Applications: Double Integrals 117
x
y
z
P
a
b
r
'
r
Figure 4.9: Electrostatic field of a flat rectangular charge distribution.
E
z
= k
e
σz
#
a/2
−a/2
dx
#
b/2
−b/2
dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
.
Note that the x
integration cannot be done until after the y
integration, because
the latter has an x
-dependent integrand.
Having exhausted the (simple) possibilities for electrostatics (and gravity,
since the two are almost identical), we now turn to magnetostatics.
Example 4.2.2.
Approximate the belt of a Van de Graff machine with an isolated
moving rectangle having sides a and b,andvelocityv along the side b as shown in
Figure 4.10. Furthermore, assume that the charges are uniformly distributed on the
belt with surface charge density σ. We want to find the magnetic field of the belt
at a general point P in space. Let us choose the positive y-direction to be that of
the velocity. Then, Equation (4.17) becomes
B(r)=k
m
##
Ω
σdav × (r −r
)
|r − r
|
3
.
The geometry of this example is identical to that of Example 4.2.1. Therefore, we
can immediately write the integral for B: magnetic field of a
charged
rectangular
moving belt
B(r)=k
m
##
Ω
σdx
dy
v
ˆ
e
y
× [(x − x
)
ˆ
e
x
+(y − y
)
ˆ
e
y
+ z
ˆ
e
z
]
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
,
from which the components of the magnetic field are easily calculated:
B
x
= k
m
σvz
#
a/2
−a/2
dx
#
b/2
−b/2
dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
,
B
y
=0, (4.27)
B
z
= −k
m
σv
#
a/2
−a/2
(x − x
) dx
#
b/2
−b/2
dy
{(x − x
)
2
+(y − y
)
2
+ z
2
}
3/2
.
P
y
z
x
r
'
Figure 4.10: A rectangular distribution of moving charges whose magnetic field can
be calculated using Cartesian coordinates.

118 Integration: Applications
4.2.2 Cylindrical Coordinates
The cylindrical system has two types of primary surface: planes and cylinders.
Although we considered planes in the previous subsection, we shall reconsider
them here because the third primary surface, that perpendicular to the z-axis,
gives us the possibility of solving planar problems with nonrectangular regions
of integration. Let us start with such a problem.
Example 4.2.3.
In this example we want to calculate the gravitational field of
a uniform surface mass distribution of density σ
m
which is a segment of a planar
annular region with inner radius a and outer radius b, and whose sides make an
angle of α as shown in Figure 4.11(a). Let us choose our origin to coincide with
the center of the annular region, our x-axis to be along one of the sides, and the
xy-plane to be the plane of the mass distribution [see Figure 4.11(b)].
Recall that in cylindrical coordinates, the components of the position vector of
P
are not the same as the source point’s coordinates.Infact,wehave
r
= ρ
ˆ
e
ρ
, r = ρ
ˆ
e
ρ
+ z
ˆ
e
z
,
r − r
= ρ
ˆ
e
ρ
+ z
ˆ
e
z
− ρ
ˆ
e
ρ
,
|r − r
|
3
=(ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+ z
2
)
3/2
,
where in the last line we have made the simplification that the field point is in the
xz-plane, so that ϕ =0;otherwise,wewouldhavecos(ϕ−ϕ
) instead of cos ϕ
.The
element of mass is given by
dm(r
)=σ
m
da(r
)=σ
m
(dρ
)(ρ
dϕ
)=σ
m
ρ
dρ
dϕ
.
Thus, the gravitational field is
g = −
##
Ω
Gdm(r
)
|r − r
|
3
(r − r
),
= −Gσ
m
#
b
a
ρ
dρ
#
α
0
dϕ
(ρ
ˆ
e
ρ
+ z
ˆ
e
z
− ρ
ˆ
e
ρ
)
(ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+ z
2
)
3/2
. (4.28)
To find the components, we take the dot product of this integral with the cylindrical
x
y
z
(a)
(b)
α
′ρ ′
ϕ
d
d
′ρ
′
ϕ
a
b
′
r
Figure 4.11: The annular region whose gravitational field is being calculated. The
position vector of the source point and the lengths of the sides of the element of area
are also shown.
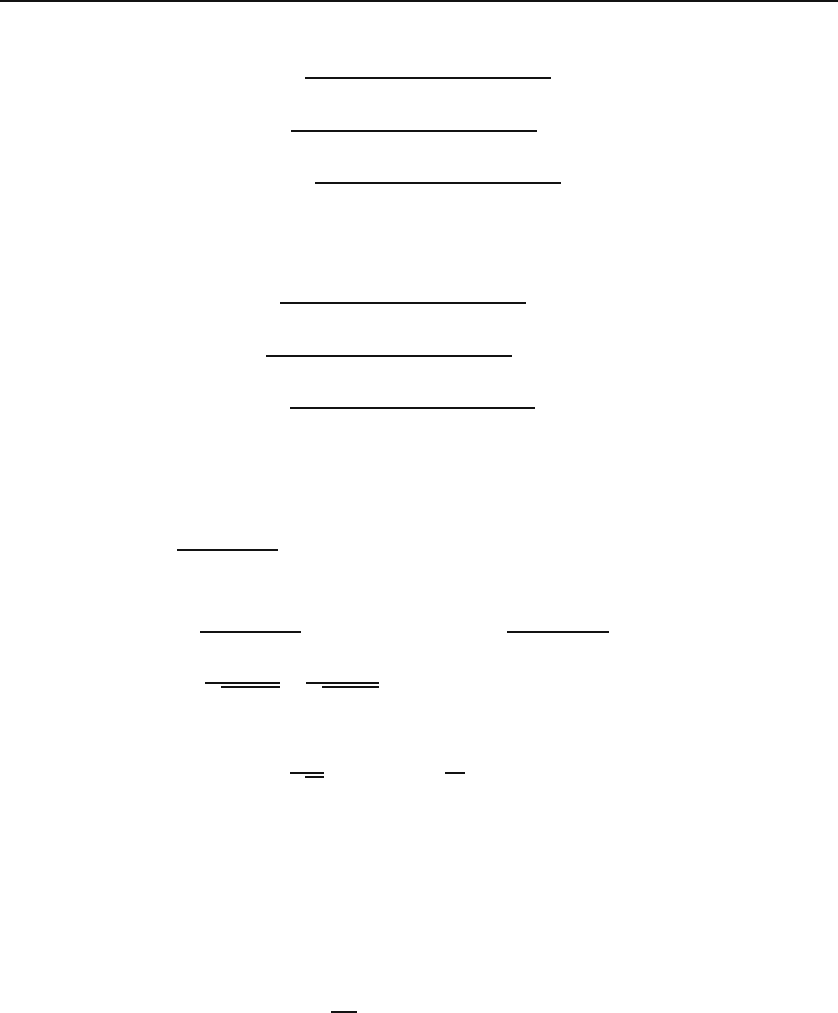
4.2 Applications: Double Integrals 119
unit vectors. The result will then be
g
ρ
= −Gσ
m
#
b
a
ρ
dρ
#
α
0
(ρ − ρ
cos ϕ
) dϕ
(ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+ z
2
)
3/2
,
g
ϕ
= Gσ
m
#
b
a
ρ
dρ
#
α
0
ρ
sin ϕ
dϕ
(ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+ z
2
)
3/2
, (4.29)
g
z
= −Gσ
m
z
#
b
a
ρ
dρ
#
α
0
dϕ
(ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+ z
2
)
3/2
.
Let us look at some special cases of this. For a complete annular region, we
simply replace α with 2π:
g
ρ
= −Gσ
m
#
b
a
ρ
dρ
#
2π
0
(ρ − ρ
cos ϕ
) dϕ
(ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+ z
2
)
3/2
,
g
ϕ
= Gσ
m
#
b
a
ρ
dρ
#
2π
0
ρ
sin ϕ
dϕ
(ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+ z
2
)
3/2
=0, (4.30)
g
z
= −Gσ
m
z
#
b
a
ρ
dρ
#
2π
0
dϕ
(ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+ z
2
)
3/2
.
As expected, the ϕ-component has disappeared.
We can further simplify the geometry by locating the field point on the z-axis.
Then, ρ =0andwehave
g
ρ
= Gσ
m
#
b
a
ρ
2
dρ
(ρ
2
+ z
2
)
3/2
#
2π
0
cos ϕ
dϕ
=0,
g
ϕ
=0,
g
z
= −Gσ
m
z
#
b
a
ρ
dρ
(ρ
2
+ z
2
)
3/2
#
2π
0
dϕ
= −2πGσ
m
z
#
b
a
ρ
dρ
(ρ
2
+ z
2
)
3/2
= −2πGσ
m
z
(
1
√
a
2
+ z
2
−
1
√
b
2
+ z
2
)
.
If we take the limit a → 0andb →∞,weobtain
g = −2πGσ
m
z
√
z
2
ˆ
e
z
= −2πGσ
m
z
|z|
ˆ
e
z
,
wherewehaveusedBox4.2.1(seebelow). Nownotethatz/|z| = ±1 depending
on the sign of z.Whenz>0, we get z/|z|
ˆ
e
z
=
ˆ
e
z
which is the unit normal to the
surface. When z<0, we get z/|z|
ˆ
e
z
= −
ˆ
e
z
which is again the unit normal to (the
other side of) the surface. Denoting the unit normal by
ˆ
e
n
,wecanwrite
g = −2πGσ
m
ˆ
e
n
.
The electrostatic analogue of this is obtained by substituting −k
e
= −1/4π
0
for G. This yields
E =
σ
q
2
0
ˆ
e
n
which is the field of an infinite sheet of charge with which the reader is familiar.
Note that while g always points toward the sheet (opposite to
ˆ
e
n
,becauseσ
m
is
always positive), the direction of E is determined by the sign of σ
q
.
120 Integration: Applications
4.2.3 Spherical Coordinates
One of the primary surfaces of a spherical coordinate system is a sphere, and
since there are a lot of spherical objects around, it is useful to gain experience
in calculations involving spheres.
In the following, we shall be taking square roots of functions. Care needs
to be taken when doing so:
Box 4.2.1. For any real-valued quantity A,
√
A
2
≡|A|, i.e., the square
root of the square of a quantity is the absolute value of that quantity.
Failure to keep this in mind will result in incorrect conclusions, as we shall
see below.
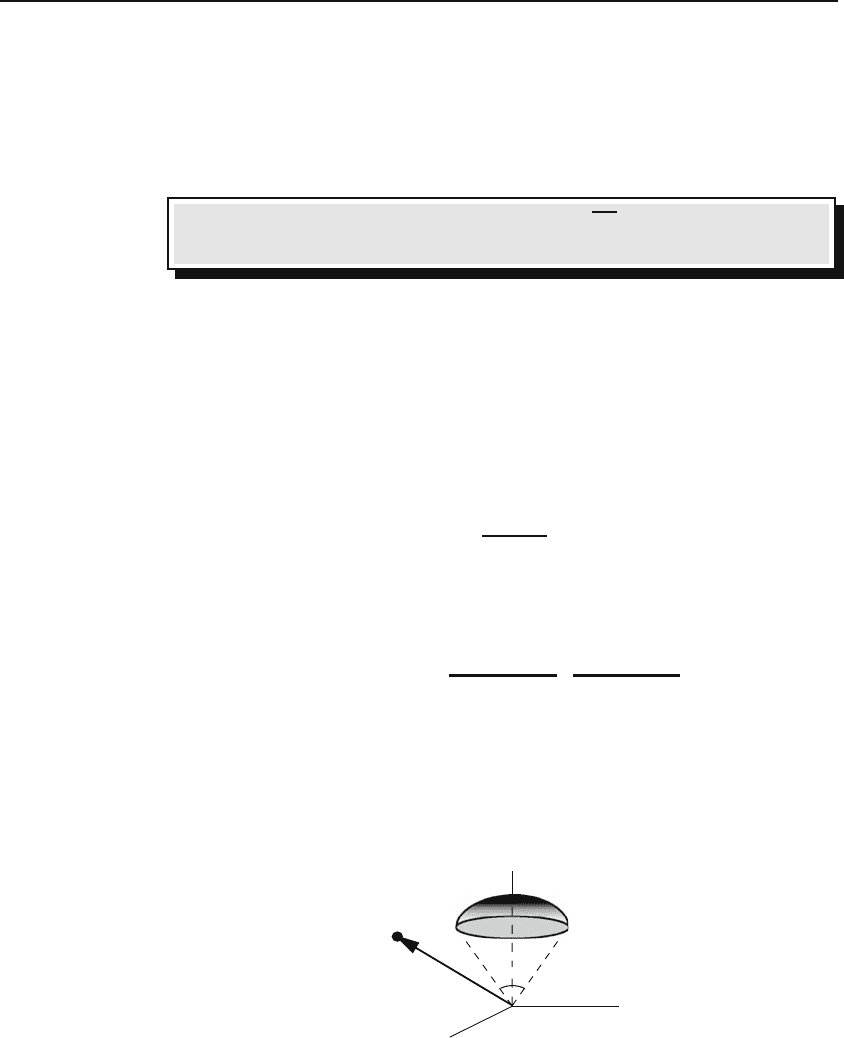
Example 4.2.4.
In this example we are interested in the gravitational field at a
general point P of a spherical cap, i.e., a segment of a spherical shell of radius a and
uniform surface density σ such that the cone defined by the segment and the center
of the sphere has a half-angle α (see Figure 4.12). It is clear that the choice of axes
and origin resulting in the greatest simplification is as shown in Figure 4.12. Notice
that P is taken to lie in the xz-plane, so that ϕ = 0. We can immediately write
g = −G
##
Ω
dm(r
)
|r − r
|
3
(r − r
) (4.31)
with
r
= a
ˆ
e
r
, r = r
ˆ
e
r
, r −r
= r
ˆ
e
r
− a
ˆ
e
r
,
|r − r
|
3
=
3
r
2
+ a
2
− 2ra
ˆ
e
r
·
ˆ
e
r
(sin θ sin θ
cos ϕ
+cosθ cos θ
)
4
3/2
, (4.32)
dm(r
)=σda
1
= σa
2
sin θ
dθ
dϕ
.
By inserting these relations in (4.31) and dotting the result with unit vectors, we
obtain the three components of g in various coordinate systems. In spherical coor-
dinates these are
P
2
α
x
y
z
r
Figure 4.12: A spherical cap whose gravitational field can be calculated using spherical
coordinates.
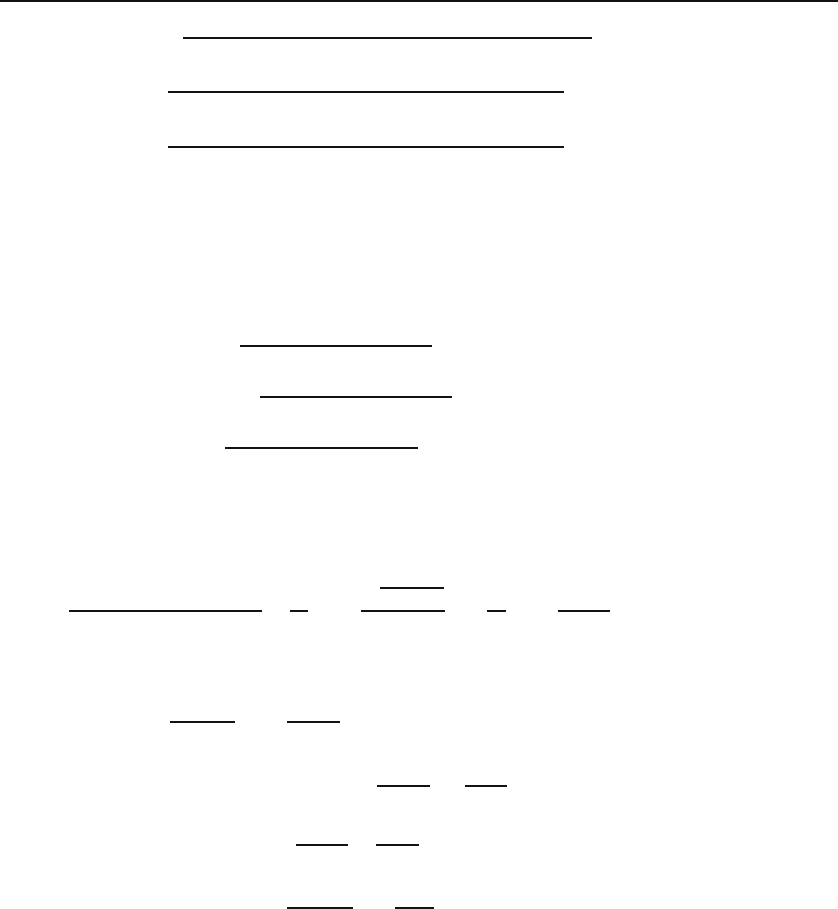
4.2 Applications: Double Integrals 121
g
r
= −Gσa
2
##
Ω
sin θ
{r −a(sin θ sin θ
cos ϕ
+cosθ cos θ
)} dθ
dϕ
{r
2
+ a
2
− 2ra(sin θ sin θ
cos ϕ
+cosθ cos θ
)}
3/2
,
g
θ
= Gσa
3
##
Ω
sin θ
(cos θ sin θ
cos ϕ
− sin θ cos θ
) dθ
dϕ
{r
2
+ a
2
− 2ra(sin θ sin θ
cos ϕ
+cosθ cos θ
)}
3/2
, (4.33)
g
ϕ
= Gσa
3
##
Ω
sin
2
θ
sin ϕ
dθ
dϕ
{r
2
+ a
2
− 2ra(sin θ sin θ
cos ϕ
+cosθ cos θ
)}
3/2
=0.
The region of integration Ω is one in which θ
varies from 0 to α,andϕ
from 0 to
2π. The last integral vanishes because of the ϕ
integration. The vanishing of the
ϕ-component is simply the result of the azimuthal symmetry.
The result above is not interesting, but if we move P to the polar axis, so that
θ = 0, then the equations simplify considerably, and we get
g
r
= −Gσa
2
#
α
0
sin θ
(r −a cos θ
) dθ
(r
2
+ a
2
− 2ra cos θ
)
3/2
#
2π
0
dϕ
= −2πGσa
2
#
α
0
sin θ
(r − a cos θ
) dθ
(r
2
+ a
2
− 2ra cos θ
)
3/2
,
g
θ
= Gσa
3
#
α
0
sin
2
θ
dθ
(r
2
+ a
2
− 2ra cos θ
)
3/2
#
2π
0
cos ϕ
dϕ
=0,
g
ϕ
=0.
The most interesting result is obtained when α = π, i.e., when we have a com-
plete spherical shell. Then using
#
π
0
sin θ
(r − a cos θ
) dθ
(r
2
+ a
2
− 2ra cos θ
)
3/2
=
1
r
2
1 −
(a − r)
2
a − r
≡
1
r
2
1 −
|a − r|
a − r
,
which can be looked up in a good integral table, we obtain
g
r
= −
2πGσa
2
r
2
1 −
|a − r|
a − r
,g
θ
=0,g
ϕ
=0.
For points inside the shell, r<a; therefore
|a − r|
a − r
=
a − r
a − r
=1,andthefield
vanishes. Thus, the gravitational field inside a spherical shell is zero. On the other gravitational field
inside a spherical
shell is zero.
hand, for points outside, r>a,and
|a − r|
a − r
=
r −a
a − r
= −1, leading to
g
r
= −
4πGσa
2
r
2
= −
GM
r
2
,
where M =4πa
2
σ is the total mass of the shell. This is identical to the gravitational
field of a point charge of mass M located at the center of the shell. Now, if we have concept of
spherical mass
distribution
elaborated
a number of concentric shells, then, at a point outside the outermost one, the field
must be that of a point charge at the common center having a mass equal to the total
mass of all the shells. Note that each shell can have a different uniform density than
others. In particular, if we have a solid sphere, with a density which is a function of
r alone, the same result holds. A density which is a function of r alone is called a
spherical mass distribution. Wethushavethefamousresult:
