Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

102 Integration: Applications
There is an alternative derivation of the last formula which relies directly
on the definition of integral. Since the velocity of the particle is changing,
we cannot find the displacement by simple multiplication with time. How-
ever, if we divide the time interval (from 0 to t)intoN small subintervals,
and concentrate on the motion of the particle in each subinterval, then each
displacement can be approximated by the product of velocity and the small
time-interval, and the total displacement r(t) − r
0
will be simply the sum of
all such displacements. This is summarized as
r(t) − r
0
≈
N
i=1
v(s
i
)Δs
i
which, in the limit of larger and larger N,gives
r(t) − r
0
=
#
t
0
v(s) ds.
Notice how careful we have been to avoid using the same variable for
integration as well as the limit of integration. This is a practice the reader
should constantly keep in mind. As a rule
important caution!
Box 4.1.1. (Caution!). Never use the same symbol for the variable of
an integral and its limits, or of an integral and of another integral of which
the first integral is the integrand.
The following example is a good illustration of the significance of the concept
of an integral and the rule in the Box above.
Example 4.1.1.
In mechanics, Newton’s second law places special importance
on acceleration,
2
and a knowledge of acceleration is normally sufficient to solve a
mechanical problem, i.e., find displacement as a function of time. A particular
example of this situation is when acceleration is known as a function of time, in
which case we can immediately find the velocity in exact analogy with Equation
(4.1). We thus have
v(t) − v
0
=
#
t
0
a(s) ds ⇒ v(t)=v
0
+
#
t
0
a(s) ds.
Notice how the argument of v is the same as the upper limit of integration. Now that
we have velocity, we can substitute it in Equation (4.1) to find the displacement.
This gives
r(t) − r
0
=
#
t
0
(
v
0
+
#
s
0
a(u) du
)
ds
or
r(t)=r
0
+ v
0
t +
#
t
0
ds
#
s
0
a(u) du.
2
Because the second law of motion connects acceleration and the cause of motion, force.

4.1 Single Integrals 103
u
s
u
line s
=
s
=
t
u
=
t
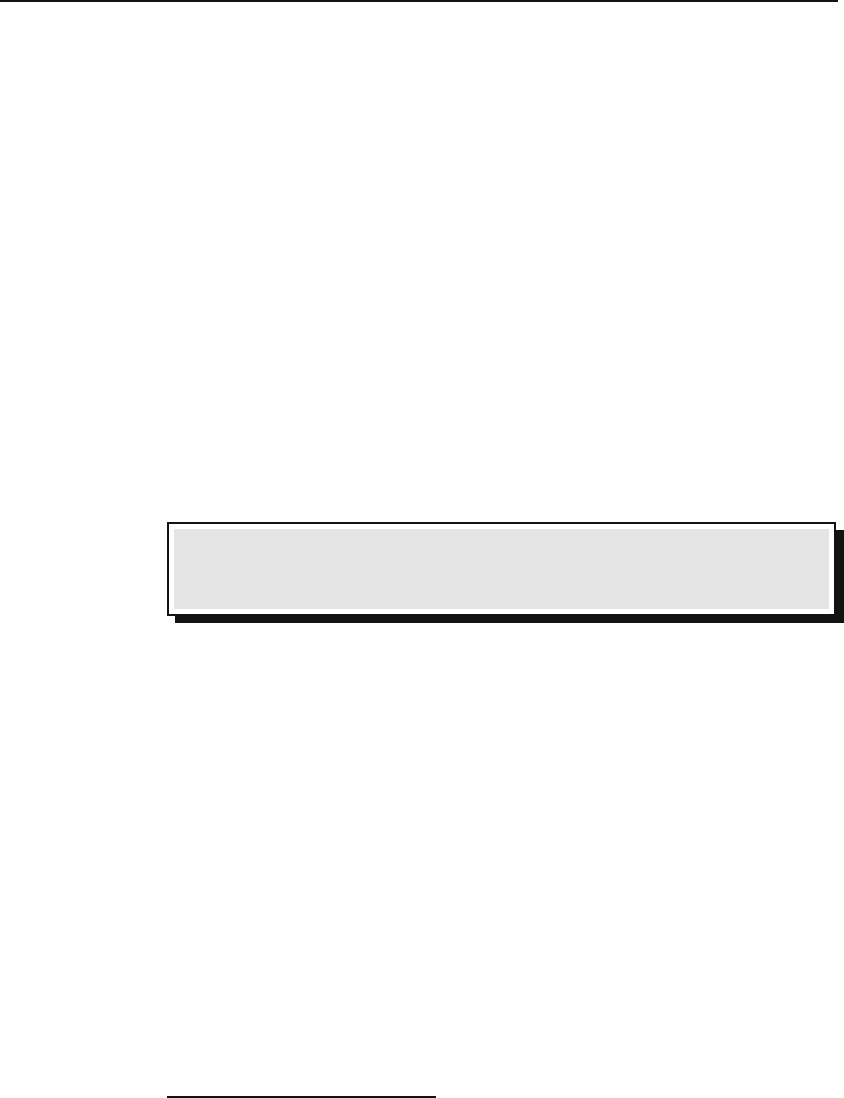
Figure 4.1: The region of integration for calculating position as a double integral.
In the double integral, it is understood that the u-integration is to be done first,
followed by the s-integration. As the last double integral suggests, the region of
integration, in the us-plane, is a right triangle bounded by the vertical axis (the s-
axis, or u = 0), the line u = s, and the horizontal line s = t asshowninFigure4.1.
It is convenient, in this case, to change the order of integration. The lower limit of given a definite
double integral,
one can
reconstruct the
region of
integration in a
plane.
the s-integral—the firstintegration—isu and the upper limit is t. Once this integral
is done, the u-integral goes from 0 to t, as can easily be verified. We, therefore, have
r(t)=r
0
+ v
0
t +
#
t
0
du
#
t
u
a(u) ds = r
0
+ v
0
t +
#
t
0
a(u) du
#
t
u
ds (4.2)
= r
0
+ v
0
t +
#
t
0
a(u)(t − u) du = r
0
+ v
0
t + t
#
t
0
a(u) du −
#
t
0
u a(u) du.
It is instructive for the reader to show that the first derivative of this expression
gives the velocity and the second derivative the acceleration.
Historical Notes
Two men are credited with the invention of calculus, Newton and Leibniz. Of course,
as we have seen, the “invention” of calculus was a long process involving many gen-
erations of mathematicians. Nevertheless, Newton and Leibniz made great contri-
butions to the subject and gave it a prominent role in the subsequent evolution of
mathematical thought.
Gottfried Wilhelm Leibniz studied law and, after defending a thesis in logic,
received a Bachelor of Philosophy degree. He wrote a second thesis on a universal
method of reasoning in 1666 which completed his work for a doctorate in philoso-
phy at the University of Altdorf and qualified him for a professorship. During the
years 1670 and 1671, Leibniz wrote his first papers on mechanics and produced his
calculating machine.
Leibniz was also involved in the politics of his time. In March, 1672, he went to
Paris on a political mission as an ambassador of the Elector of Mainz. While in Paris,
he made contact with notable mathematicians and scientists including Huygens.This
stirred up his interest in mathematics, a subject that he knew nothing about prior
to 1672. In 1673 he went to London and met other scientists and mathematicians
including the secretary of the Royal Society of London.
Gottfried Wilhelm
Leibniz 1646–1716
While making his living as a diplomat, he delved further into mathematics and
read Descartes and Pascal. In 1676 Leibniz was appointed librarian and councilor to
the Elector of Hanover. Twenty-four years later the Elector of Brandenburg invited

104 Integration: Applications
Leibniz to work for him in Berlin. While involved in many political maneuvers,
including the succession of George Ludwig of Hanover to the English throne, Leibniz
worked in many fields and his side activities encompassed an enormous range. He
died in 1716, undeservedly neglected.
In addition to being a diplomat, Leibniz was a philosopher, lawyer, historian,
and pioneer geologist. He did important work in logic, mathematics, optics, me-
chanics, hydrostatics, nautical science, and calculating machines. Although law was
his profession, his contributions to mathematics and philosophy are among the best.
He tried endlessly to reconcile the Catholic and Protestant faiths. He founded the
Berlin Academy in 1700. He criticized the universities for being “monkish” and
charged that they possessed learning but no judgment and were absorbed in trifles.
Instead he urged that true knowledge—mathematics, physics, chemistry, anatomy,
botany, zoology, history, and geography be pursued. He favored the German lan-
guage over Latin because Latin was tied to the older, useless thought. Men mask
their ignorance, he said, by using the Latin language to impress people.
His numerous mathematical notes on differentiation and integration is full of
novel ideas. His notations were quite ingenious: He introduced the notation dy/dx
for the derivative and
for the integral. He recognized the operations of integration
and differentiation as the inverse of one another.
4.1.2 Examples from Electrostatics and Gravity
In electrostatics or magnetostatics, one is sometimes interested in calculating
the electric or magnetic field of a linear charge or current distribution. In
electrostatics, one can imagine sprinkling electric charges on a thin piece of
string and asking for the electric field of the charge distribution. In magne-
tostatics, one flows an electric current through a thin wire and asks for the
resulting magnetic field. In general, the string or the wire, being a curve in
space, has a parametric equation given, in Cartesian coordinates say, by
f(t),g(t),h(t)
!
,wheref, g,andh are known functions of the parameter t.
The problems of gravity are entirely analogous to those of electrostatics. The
master equation of electrostatocs is Equation (3.3) which we reproduce here
for convenience:
E =
##
Ω
k
e
dq(r
)
|r −r
|
3
(r − r
), Φ=
##
Ω
k
e
dq(r
)
|r − r
|
. (4.3)
Cartesian Coordinates
Let us assume that Cartesian coordinates are suitable for the problem, and we
want to calculate the electrostatic field at a point P with coordinates (x, y, z)
as shown in Figure 4.2. We reduce the integrals in Equation (4.3) to single
integrals by calculating their various parts entirely in terms of t.Firstwe
note that the source point P
lies on the curve, and therefore, its coordinates
(x
,y
,z
) are functions of t. Since we are using Cartesian coordinates, the
components of the position vector of P
are the same as the source point’s
coordinates. Therefore, r
= x
ˆ
e
x
+ y
ˆ
e
y
+ z
ˆ
e
z
= x
,y
,z
.

4.1 Single Integrals 105
P
dl
r
r
'
x
y
z
Figure 4.2: Electrostatic field of a general linear charge distribution.
The element of charge
dq(r
)=λ(r
) dl(r
)=λ(r
)
(dx
)
2
+(dy
)
2
+(dz
)
2
(4.4)
turns into a function of t (times dt) after the substitutions:
x
= f(t),y
= g(t),z
= h(t),
dx
= f
(t)dt, dy
= g
(t)dt, dz
= h
(t)dt.
Similarly,
r −r
= x
ˆ
e
x
+ y
ˆ
e
y
+ z
ˆ
e
z
− x
ˆ
e
x
− y
ˆ
e
y
− z
ˆ
e
z
=(x −x
)
ˆ
e
x
+(y − y
)
ˆ
e
y
+(z − z
)
ˆ
e
z
(4.5)
and
|r − r
| =
(x −x
)
2
+(y − y
)
2
+(z − z
)
2
,
|r − r
|
3
=
*
(x − x
)
2
+(y − y
)
2
+(y − y
)
2
+
3/2
. (4.6)
Substituting all the above in Equation (4.3) yields an integral in t for E and
another integral in t for Φ. The limits of these integrals are determined from
the parametric equation of the curve describing the linear charge distribution.
As a general rule, in order to find the components of the field along a unit
vector, we use Box 1.1.2, i.e., we take the dot product of the field with that
unit vector. This involves taking the dot product of the integrand with the
unit vector. In the case of Cartesian unit vectors, this procedure simply picks
out the integral multiplying one of the unit vectors. For other coordinate
systems, this is not the case, as we shall see shortly.
Box 4.1.2. Although the geometry of the source (charge distribution) may
dictate a particular coordinate system, the components of the field can be
calculated in any coordinate system desired.

106 Integration: Applications
Thus, by multiplying the integrand by
ˆ
e
ρ
,
ˆ
e
ϕ
,and
ˆ
e
z
and expressing the dot
products
ˆ
e
ρ
·
ˆ
e
x
,
ˆ
e
ϕ
·
ˆ
e
x
, etc., in terms of Cartesian coordinates, we can obtain
E
ρ
, E
ϕ
,andE
z
as integrals over t. A similar derivation gives the electric
potential Φ as an integral over t. Although a formula can be obtained for the
components of the electric field for a general curve (see Problem 4.3), it is
best to learn the formalism by an example.
Example 4.1.2.
The simplest example of the general discussion above is a thin
rod of length L that is uniformly charged with constant linear density λ.Wewant
to find the electric field and the electrostatic potential at an arbitrary point P in
space, as shown in Figure 4.3(a).
As discussed at the beginning of this section, it pays to choose one’s coordinates
wisely. Clearly, the rod defines an axis naturally. So, let us choose our z-axis to lie
along the rod. Once this is done, we are free to move the origin up and down, and
orient the x-andy-axes. Let us use this freedom to put the field (or observation)
point P on the x-axis. We then have a situation depicted in Figure 4.3(b).
To continue, we need the parametric equation of the rod. Clearly, the x
and
y
parts have the (unique) “parameterization” x
=0andy
= 0. There are many
ways to parameterize the z
part of the curve. However, in situations involving only
one coordinate, it is most natural to set that coordinate equal to the parameter t.
So, we choose the following simple parameterization:
x
=0,y
=0,z
= t, a ≤ t ≤ a + L ≡ b.
Substituting this and r = x
ˆ
e
x
in Equations (4.5) and (4.6) yields
r − r
= x
ˆ
e
x
− t
ˆ
e
z
,
as well as |r −r
| =
√
x
2
+ t
2
and |r − r
|
3
=(x
2
+ t
2
)
3/2
.
Putting all this in Equation (4.3) yields
E(x, y, z)=
#
b
a
k
e
λdt
(x
2
+ t
2
)
3/2
(x
ˆ
e
x
− t
ˆ
e
z
) dt (4.7)
P
P
E
z
E
x
E
x
y
z
a
L
(a)
(b)
Figure 4.3: Electrostatic field of a uniformly charged rod of length L.(a)Thepoint
P and the rod, and (b) a convenient Cartesian coordinate system for the calculation of
the field. The figure assumes a negative λ.
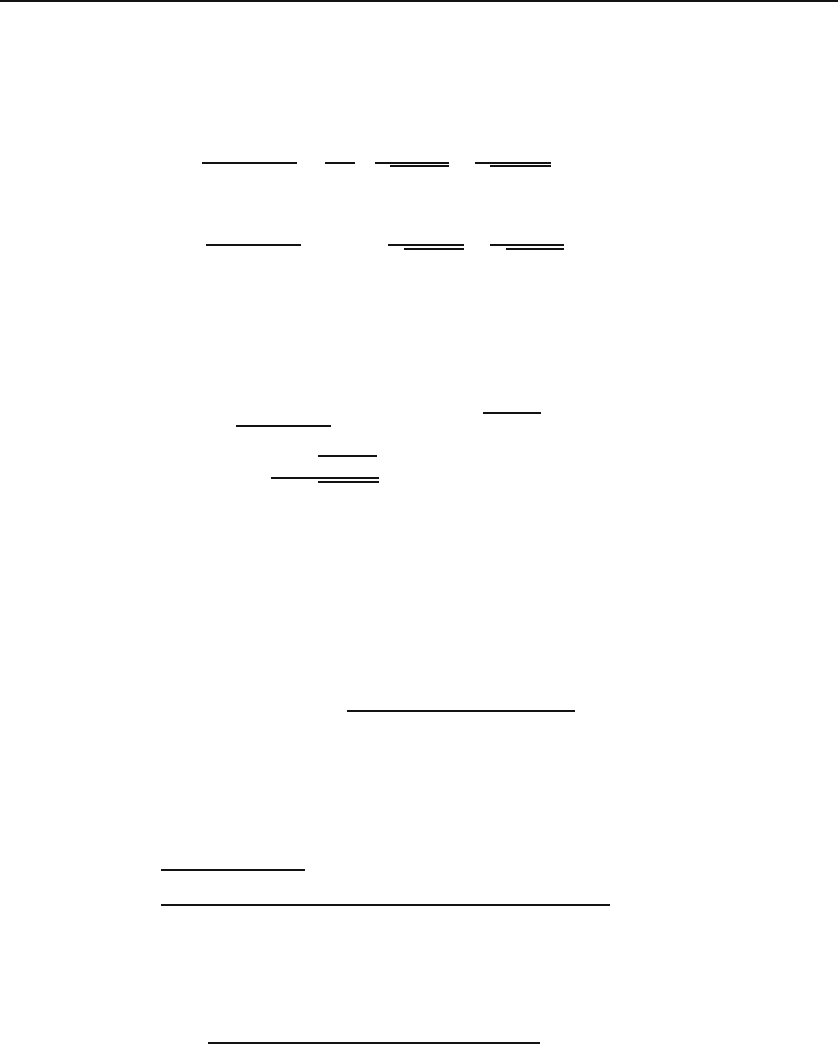
4.1 Single Integrals 107
To find the components of the field in any coordinate system, dot-multiply Equation
(4.7) by the unit vectors of that coordinate system. For Cartesian components,
E
x
= E ·
ˆ
e
x
, which picks the term multiplying
ˆ
e
x
in (4.7); E
y
= E ·
ˆ
e
y
,whichis
zero; E
z
= E ·
ˆ
e
z
, which picks the term multiplying
ˆ
e
z
in (4.7). Thus,
E
x
= k
e
λx
#
b
a
dt
(x
2
+ t
2
)
3/2
=
k
e
λ
x
b
√
x
2
+ b
2
−
a
√
x
2
+ a
2
,
E
y
=0, (4.8)
E
z
= −k
e
λ
#
b
a
tdt
(x
2
+ t
2
)
3/2
= −k
e
λ
1
√
x
2
+ a
2
−
1
√
x
2
+ b
2
.
It is instructive to consider special cases of these formulas, such as when a = −L/2
and b =+L/2 (especially when L is large compared to x), which may be more
familiar to the reader. We leave such considerations as exercises.
The electrostatic potential can be obtained similarly. From Equation (4.3), we
get
Φ(x, y, z)=
#
b
a
k
e
λ
(x
2
+ t
2
)
1/2
dt = k
e
λ ln(t +
x
2
+ t
2
)
b
a
= k
e
λ ln
b +
√
x
2
+ b
2
a +
√
x
2
+ a
2
.
Cylindrical Coordinates
For cylindrical coordinates the components of the position vector of P
are caution!
coordinates and
components are
not the same.
not the same as the coordinates of P
.Infact,r
= ρ
ˆ
e
ρ
+ z
ˆ
e
z
.
Various parts of the “master” equation (4.3) [or (3.3)] can be calculated
as before—this time, of course, in cylindrical coordinates—and the results
substituted in it to arrive at the expression for E entirely in terms of t.Thus
dq(r
)=λ(r
) dl(r
)=λ(r
)
(dρ
)
2
+ ρ
2
(dϕ
)
2
+(dz
)
2
, (4.9)
where use has been made of Equation (2.29). Similarly, we have
r −r
= ρ
ˆ
e
ρ
+ z
ˆ
e
z
− ρ
ˆ
e
ρ
− z
ˆ
e
z
= ρ
ˆ
e
ρ
− ρ
ˆ
e
ρ
+(z − z
)
ˆ
e
z
(4.10)
which leads to the absolute value
|r − r
| =
(r − r
) ·(r −r
)
=
[ρ
ˆ
e
ρ
− ρ
ˆ
e
ρ
+(z − z
)
ˆ
e
z
] · [ρ
ˆ
e
ρ
− ρ
ˆ
e
ρ
+(z − z
)
ˆ
e
z
].
Carrying out the dot product and keeping in mind that
ˆ
e
ρ
and
ˆ
e
ρ
are neither
the same nor perpendicular to each other, but make the two different angles
ϕ and ϕ
with the x-axis, we obtain
|r − r
| =
ρ
2
+ ρ
2
− 2ρρ
cos
ϕ −ϕ
!
+(z − z
)
2
,
|r − r
|
3
=
,
ρ
2
+ ρ
2
− 2ρρ
cos
ϕ −ϕ
!
+(z − z
)
2
-
3/2
.
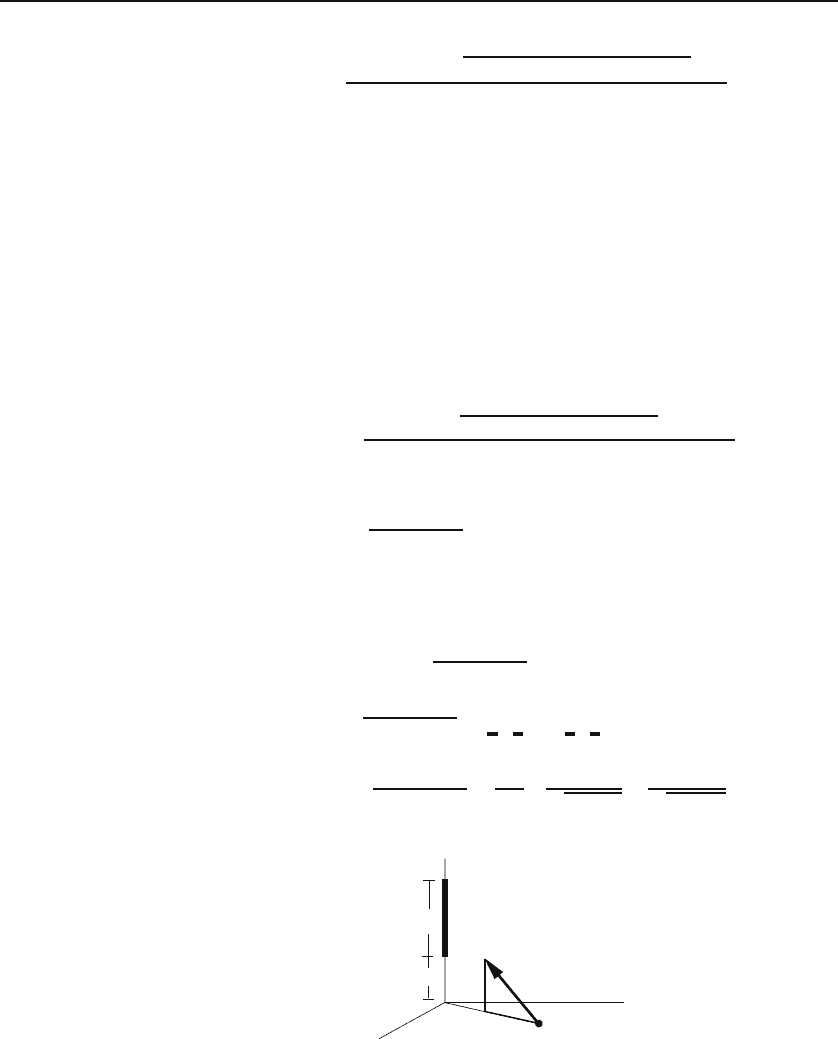
108 Integration: Applications
Putting everything together, we obtain
E =
##
Ω
k
e
λ(r
)
(dρ
)
2
+ ρ
2
(dϕ
)
2
+(dz
)
2
,
ρ
2
+ ρ
2
− 2ρρ
cos
ϕ −ϕ
!
+(z − z
)
2
-
3/2
×
ρ
ˆ
e
ρ
− ρ
ˆ
e
ρ
+(z − z
)
ˆ
e
z
!
. (4.11)
To find components in any coordinate system, use Box 1.1.2 and take the dot
product of Equation (4.11) with the appropriate unit vectors. The electro-
static potential is derived in a similar way.
Example 4.1.3.
Let us reconsider the example of a rod. Obviously we should
choose our z-axis along the rod. We further move the origin so that P ends up in the
xy-plane (see Figure 4.4). This will reduce r to ρ
ˆ
e
ρ
. The simplest parameterization
of the rod is
ρ
=0,z
= t, a ≤ t ≤ a + L ≡ b.
We note that ϕ
is undefined. This poses no problem because, as will be seen below,
it will drop out of the equations. Putting these in Equation (4.11) we obtain
E = k
e
λ
##
Ω
(0)
2
+(0)(dϕ
)
2
+(dz
)
2
,
ρ
2
+(0)
2
− 2ρ(0) cos
ϕ − ϕ
!
+(0− z
)
2
-
3/2
×
.
ρ
ˆ
e
ρ
+(0)
ˆ
e
ρ
+(0− z
)
ˆ
e
z
/
(4.12)
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
− t
ˆ
e
z
!
To find the components of the electric field, take the dot product of one of the
unit vectors of a coordinate system and Equation (4.12). For the ρ component, we
have
E
ρ
= E ·
ˆ
e
ρ
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
− t
ˆ
e
z
!
·
ˆ
e
ρ
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
·
ˆ
e
ρ
=1
−t
ˆ
e
z
·
ˆ
e
ρ
=0
!
(4.13)
= k
e
λρ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
=
k
e
λ
ρ
0
b
ρ
2
+ b
2
−
a
ρ
2
+ a
2
1
;
x
y
z
P
ρ
E
z
E
ρ
E
a
L
Figure 4.4: Electrostatic field of a uniformly charged rod of length L in cylindrical
coordinates. The figure assumes a negative λ.

4.1 Single Integrals 109
for the ϕ component, we obtin
E
ϕ
= E ·
ˆ
e
ϕ
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
− t
ˆ
e
z
!
·
ˆ
e
ϕ
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
·
ˆ
e
ϕ
=0
−t
ˆ
e
z
·
ˆ
e
ϕ
=0
!
=0. (4.14)
Note how the dependence on ϕ has completely disappeared because of the azimuthal
symmetry of the rod. Finally the z component is
E
z
= E ·
ˆ
e
z
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
− t
ˆ
e
z
!
·
ˆ
e
z
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
·
ˆ
e
z
=0
−t
ˆ
e
z
·
ˆ
e
z
=1
!
(4.15)
= −k
e
λ
#
b
a
tdt
(ρ
2
+ t
2
)
3/2
= k
e
λ
0
1
ρ
2
+ b
2
−
1
ρ
2
+ a
2
1
The electrostatic potential Φ can be calculated similarly.
We can also find the components in Cartesian coordinates by dot-multiplying
Equation (4.12) with Cartesian unit vectors. For example,
E
x
= E ·
ˆ
e
x
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
− t
ˆ
e
z
!
·
ˆ
e
x
= k
e
λ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
ρ
ˆ
e
ρ
·
ˆ
e
x
=cos ϕ
−t
ˆ
e
z
·
ˆ
e
x
=0
!
,
= k
e
λρ cos ϕ
#
b
a
dt
(ρ
2
+ t
2
)
3/2
=
k
e
λ cos ϕ
ρ
0
b
ρ
2
+ b
2
−
a
ρ
2
+ a
2
1
E
y
will be the same except that instead of cos ϕ it will have sin ϕ,andE
z
will
be identical to the E
z
of Equation (4.15). When ϕ = 0, we recover the result of
Example 4.1.2, because ρ = x when ϕ =0.
All the foregoing derivations in electrostatics can be applied almost ver-
batim to the theory of gravitation. The only difference is the appearance of
G instead of k
e
and the interpretation of λ as linear mass density.
4.1.3 Examples from Magnetostatics
Probably the most realistic physical application of single integrals appears in
the calculation of magnetic fields of currents in (thin) wires. Before looking
at examples, let us briefly review magnetism.
We already mentioned in Chapter 1 that the magnetic field of N (slowly)
moving point charges is given by
3
B =
N
k=1
k
m
q
k
v
k
× (r − r
k
)
| r − r
k
|
3
. (4.16)
3
“Slow” compared to the speed of light which is 3 × 10
8
m/s.
110 Integration: Applications
v
j
Δ
q
j
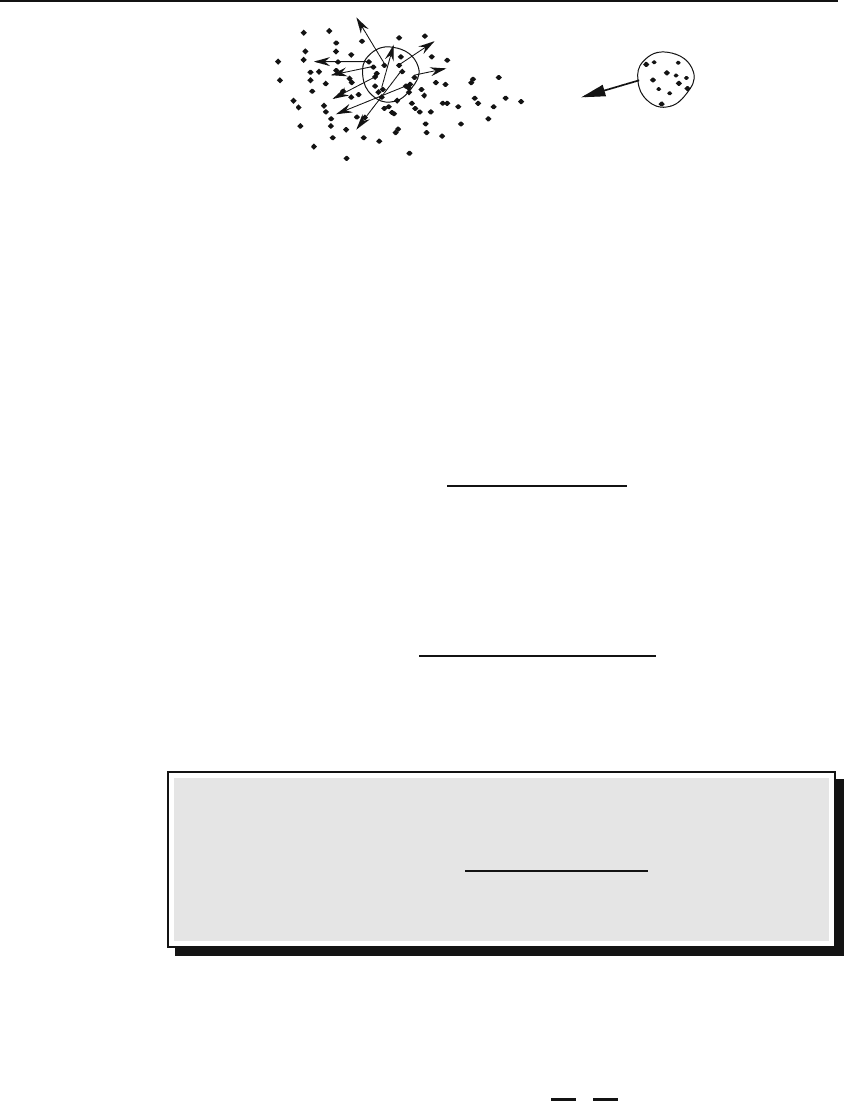
(a) (b)
Figure 4.5: Magnetic field of a moving charge distribution. (a) All charges in motion
with a “sample” singled out. The vectors show the velocities of some of the charges in
the sample. (b) The sample is described by a charge Δq
j
and an average velocity v
j
.
In a typical situation, N is of the order of 10
25
or more. So, instead of
adding all the terms individually, we lump together those that are close to
one another, i.e., in a small region, and subsequently describe the situation
by a current density (see Figure 4.5). This boils down to writing Equation
(4.16) as
B ≈
M
j=1
k
m
Δq
j
v
j
× (r − r
j
)
|r − r
j
|
3
,
where Δq
j
is the amount of charge in the jth region, v
j
is the average velocity
of all charges in the jth region, and r
j
is the position vector of the “center”
of the jth region. We can rewrite the equation above as
B ≈
M
j=1
k
m
[Δq(r
j
)v(r
j
)] ×(r −r
j
)
|r − r
j
|
3
.
In the limit that M →∞and Δq → 0, we obtain
Biot–Savart law
Box 4.1.3. The magnetic field of a moving charge distribution is given
by
B(r)=k
m
##
Ω
dq(r
)v(r
) ×(r − r
)
|r − r
|
3
. (4.17)
This is the most general form of the Biot–Savart law.
The product of the element of charge and velocity appearing in the equa-
tion is related to the various forms of current we may encounter. These are
described below:
volume current density: dq(r
)v(r
)=ρ(r
)v(r
)
≡J(r
)
dV (r
) ≡ J(r
) dV (r
),

4.1 Single Integrals 111
surface current density: dq(r
)v(r
)=σ(r
)v(r
)
≡j(r
)
da(r
) ≡ j(r
) da(r
),
linear current density: dq(r
)v(r
)=λ(r
)v(r
)
≡I(r
)
dl(r
) ≡ I(r
) dl(r
).
The volume current density J(r
) describes a situation in which charges are
free to move in all directions. The surface current density j(r
)isusedwhen
charges are confined to a surface. The most familiar current density is the
linear current density which is usually rewritten as
I(r
) dl(r
)=Id
l(r
)=Idr
.
This follows from the fact that I(r
) is in the same direction as the velocity
(at r
) which, since charges are confined to a curve (the wire), has the same
direction as the (infinitesimal) tangent displacement along the wire, namely
dr
.
We are particularly interested in the linear case as shown in Figure 4.6.
Thus, assuming that the current I is constant—it has to be due to charge
Biot–Savart law
for circuits
conservation—we obtain
Box 4.1.4. The general expression for the magnetic field of a circuit is
given by
B(r)=k
m
I
2
dr
× (r − r
)
| r − r
|
3
, (4.18)
where the circle on the integral sign implies a closed loop.
This equation is independent of any coordinate systems. We now specialize
to Cartesian and cylindrical systems.
P
d
l
r
x
y
z
dB
′
r
Figure 4.6: A general current filament described parametrically and used to calculate
the magnetic field in Cartesian coordinates.
