Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 555

Finally, the concept of optimality with respect to a Lyapunov function

introduced in Problem 8.3 is du e to Berns tein [43] w hile the inverse optimal

controller for J-Q type sys tems introduced in Problem 8.13 and the inverse

optimal controller for the minimum ph ase system introduced in Prob lem

8.14 is due to Wan and Bern s tein [449]. The concept of the pointwise

control min imization for generating control Lyapunov functions introduced

in Problem 8.20 is due to Freeman and Primbs [129].

NonlinearBook10pt November 20, 2007

Chapter Nine

Inverse Optimal Control and Integrator

Backstepping

9.1 Introduction

Control system designers have usually resorted to Lyapunov methods [445]

in order to obtain stabilizing controllers for nonlinear systems. In particular,

for smooth feedback, Lyapunov-based methods were inspired by Jur djevic

and Quinn [224] who give suﬃcient conditions for smooth stabilization b ased

on the ability of constructing a Lyapun ov function for the closed-loop system

[434]. Unfortunately, however, there does not exist a un iﬁed procedu re for

ﬁnding a Lyapunov function candidate that will stabilize the closed-loop

system for general nonlinear systems. Recent work involving diﬀerential

geometric methods [212, 336] has made the d esign of controllers for certain

classes of nonlinear systems more methodical. Such frameworks in clude the

concepts of zero dynamics and feedback linearization and require that the

system zero dynamics are asymptotically stable, ensuring the existence of

globally deﬁned diﬀeomorph ism s to transf orm the nonlinear system into a

normal form [212,336]. These techniques, however, usually rely on canceling

out system nonlinearities using feedback and may therefore lead to ineﬃcient

designs since feedback linearizing controllers may generate unnecessarily

large control eﬀort to cancel beneﬁcial system nonlinearities.

Backstepping control has recently received a great deal of attention in

the nonlinear control literature [222, 230, 246, 249, 392]. The popu larity of

this control methodology can be explained in a large part due to the fact

that it provides a framework for designing stabilizing nonlinear controllers

for a large class of nonlinear dynamical cascade systems. This framework

guarantees stability by providing a systematic procedure for ﬁnding a

Lyapunov function for the closed-loop system and choosing the control such

that the time derivative of the L yapunov function along the trajectories of

the closed-loop dynamical system is negative. Furthermore, the controller is

obtained in such a way th at the nonlinearities of the dynamical system,

which may be useful in reaching performance objectives, need not be

NonlinearBook10pt November 20, 2007

558 CHAPTER 9

canceled as in state or outpu t feedback linearization techn iques. Using this

framework, the control sys tem designer has a signiﬁcant amount of freedom

in designing the controller to address speciﬁc performance objectives w hile

guaranteeing closed-loop stability.

In [126,127] optimal pointwise min-norm state tracking controllers are

obtained for feedback linearizable systems by computing pointwise solutions

of a s tatic quadratic programming problem. A trade-oﬀ between control

eﬀort and tracking error is automatically taken into account in designing

these controllers. The optimality of this control design method relies on

the fact that every Lyapunov function solves the Hamilton-Jacobi-Bellman

equation associated with a cost functional. However, this theory does

not present a natural extension to the larger class of systems for which

recursive b ackstepping is applicable. In p articular, it is noted in [247] that

for recursive control s chemes such as backstepping, optimization of partial

cost functionals at each step will by no means result in overall optimization.

Backstepping does, however, utilize a Lyapunov function for the overall

system based on stabilizing fu nctions (virtual controls) which are deﬁned

at each recursion step. This Lyapunov function can be used to derive a

performance criterion for which the overall control, consisting of the control

law obtained at the ﬁnal and intermediate steps, is optimal.

In this chapter, we extend the optimality-based n onlinear control fra-

mework developed in Chapter 8 to cascade and block cascade systems for

which the backstepping control design methodology is applicable. The key

motivation for developing an optimal and inverse optimal nonlinear back-

stepping control theory is that it provides a family of candidate backstepping

controllers parameterized by the cost functional that is minimized. In order

to ad dress the optimality-based backstepping nonlinear control problem

we use the nonlinear-nonquadratic optimal control framework developed in

Chapter 8 to show that a particular controller derived via backstepping

methods corresponds to the solution of an optimal control problem that

minimizes an inverse nonlinear-nonquadratic performance criterion. This is

accomplished by choosing the controller such that th e Lyapunov derivative is

negative along the closed-loop system trajectories while pr oviding suﬃ cient

conditions for the existence of asymptotically stabilizing solutions to the

Hamilton-Jacobi-Bellman equation. Thus, our results allow us to derive

globally asymptotically stabilizing backstepping controllers for nonlinear

systems that minimize a derived nonlinear-nonquadratic performance func-

tional.

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 559

9.2 Cascade and Block Cascade Control Design

In this section, we consider the nonlinear cascade system

˙x(t) = f(x(t)) + G(x(t))ˆx(t), x(0) = x

, t ≥ 0, (9.1)

ˆx(t) = u(t), ˆx(0) = ˆx

, (9.2)

where x ∈ R

, ˆx ∈ R

, f : R

→ R

satisﬁes f(0) = 0, and G : R

→ R

Here, we seek a globally stabilizing feedback controller f or (9.1) and (9.2). To

introduce the integrator backstepping approach note that (9.1) and (9.2) can

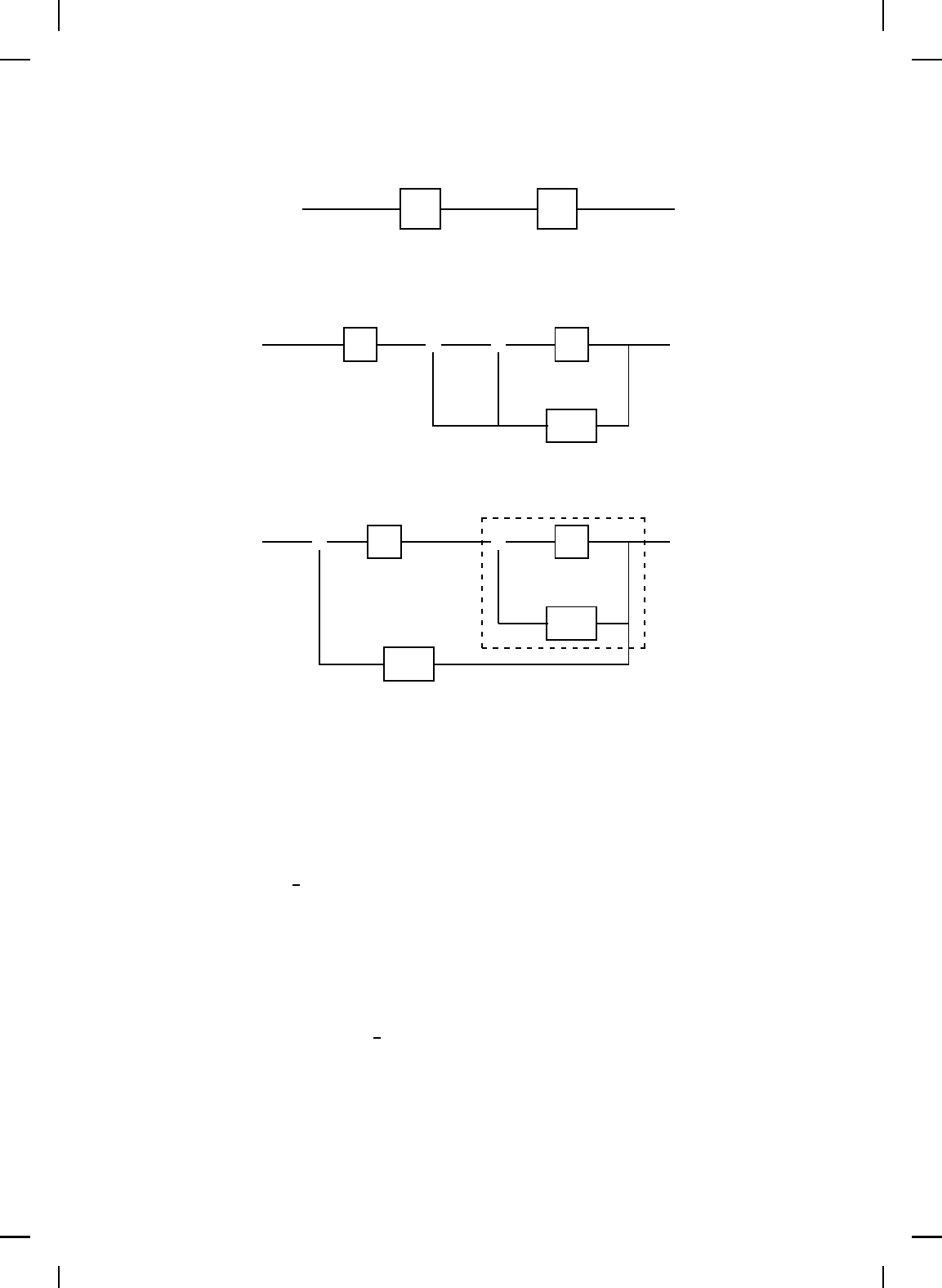
be viewed as a cascade connection of two dynamical subsys tems, as shown

in Figure 9.1(a). Speciﬁcally, the ﬁrst subsystem is (9.1) with input ˆx and

the second subsys tem consists of m integrators. Next, we assume that there

exists a continuously diﬀerentiable function α : R

→ R

such that the zero

solution x(t) ≡ 0 of the ﬁrst subsystem (9.1) is asymptotically stable with ˆx

replaced by α(x). In this case, it follows from Theorem 3.9 th at there exists

a continuously diﬀerentiable positive-deﬁnite function V

sub

: R

→ R such

that

′

sub

(x)[f(x) + G(x)α(x)] < 0, x ∈ R

, x 6= 0. (9.3)

Next, adding and subtracting G(x)α(x), x ∈ R

, to and f rom (9.1)

yields the equivalent dynamical system

˙x(t) = f (x(t)) + G(x(t))α(x(t)) + G(x(t))[ˆx(t) −α(x(t))],

x(0) = x

, t ≥ 0, (9.4)

ˆx(t) = u(t), ˆx(0) = ˆx

, (9.5)

shown in Figure 9.1(b). Introducing the change of variables z(t)

△

= ˆx(t) −

α(x(t)) yields

˙x(t) = f(x(t)) + G(x(t))α(x(t)) + G(x(t))z(t), x(0) = x

, t ≥ 0, (9.6)

˙z(t) = u(t) − ˙α(x(t)), z(0) = z

. (9.7)

As shown in Figure 9.1(c), transforming (9.1) and (9.2) to (9.6) and (9.7)

can be viewed as “backstepping” −α(x) through the integrator subsystem.

Now, with v(t)

△

= u(t) − ˙α(x(t)), (9.6) and (9.7) reduces to

˙x(t) = f(x(t)) + G(x(t))α(x(t)) + G(x(t))z(t), x(0) = x

, t ≥ 0, (9.8)

˙z(t) = v(t), z(0) = z

, (9.9)

which, when z(t) is bounded and z(t) → 0 as t → ∞, is an asymptotically

stable cascade system (see Proposition 4.2).

Exploiting this feature, we can stabilize the overall system by consid-

ering the Lyapunov function candid ate

V (x, ˆx) = V

sub

(x) + (ˆx −α(x))

P (ˆx − α(x)), (9.10)

NonlinearBook10pt November 20, 2007

560 CHAPTER 9

ˆx

(a)

ˆx

⊖

⊕



α(x)

(b)

⊖

ˆx −α(x)

⊕



α(x)



˙α(x)

(c)

Figure 9.1 Visualization of integrator backstepping.

where P ∈ R

m×m

is an arbitrary positive-deﬁnite matrix. In th is case, the

Lyapunov derivative is given by

V (x, ˆx) = V

′

sub

(x)[f(x) + G(x)α(x)] + V

′

sub

(x)G(x)z + 2z

P v. (9.11)

Letting v = −

−1

(x)V

′T

sub

(x) − kz, where k > 0, yields

V (x, ˆx) = V

′

sub

(x)[f(x) + G(x)α(x)] − k(ˆx − α(x))

P (ˆx −α(x))

< 0, (x, ˆx) ∈ R

× R

, (x, ˆx) 6= (0, 0). (9.12)

Hence, the control law

u = v + ˙α(x)

= −k(ˆx − α(x)) −

−1

(x)V

′T

sub

(x) + α

′

(x)[f(x) + G(x)ˆx)], (9.13)

stabilizes the nonlinear cascade system (9.1) and (9.2). Using the above

results the following proposition is immediate.

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 561

Proposition 9.1. Consider th e nonlinear cascade system (9.1) and

(9.2). Assume that there exist a continuously diﬀerentiable fu nction α :

→ R

and a continuously diﬀerentiable radially unbounded function

sub

: R

→ R such that

α(0) = 0, (9.14)

sub

(0) = 0 (9.15)

sub

(x) > 0, x ∈ R

, x 6= 0, (9.16)

′

sub

(x)[f(x) + G(x)α(x)] < 0, x ∈ R

, x 6= 0. (9.17)

Then, the zero solution (x(t), ˆx(t)) ≡ (0, 0) of the cascade system (9.1) and

(9.2) is globally asymp totically stable with the feedback control law (9.13).

Example 9.1. Consider the nonlinear cascade system

˙x

(t) = −

(t) −

(t) −x

(t), x

(0) = x

, t ≥ 0, (9.18)

˙x

(t) = u(t), x

(0) = x

. (9.19)

Here, we seek a globally stabilizing controller for (9.18) and (9.19) u s ing

the integrator backstepping approach. Note that (9.18) and (9.19) has the

correct form for the application of Proposition 9.1 where (9.18) makes up the

nonlinear subsystem and x

is the integrator state. Speciﬁcally, (9.18) and

(9.19) can be wr itten in the form of (9.1) and (9.2) where x = x

, ˆx = x

and

f(x) = −

−

, G(x) = −1.

To apply Proposition 9.1 we require a stabilizing f eedback for the

subsystem (9.18) and a corresponding Lyapunov function V

sub

(x) such that

(9.14)–(9.17) are satisﬁed. For the n on linear subsystem (9.18) we choose the

Lyapunov function candidate

sub

(x) = x

(9.20)

and the stabilizing feedback control

α(x) = −

. (9.21)

It is straightforward to show that (9.20) and (9.21) satisfy conditions (9.14)–

(9.17) of Proposition 9.1. Now, it follows from Proposition 9.1 that the

control law given by (9.13), that is,

u = −k(x

) + P

−1

+ 3x

(

+ x

), (9.22)

where k and P are positive constants, is a globally stabilizing feedback

control law for the overall system (9.18) and (9.19). △

Example 9.2. Consider the nonlinear cascade system

˙x

(t) = −

(t)[

(t) + 2x

(t) + x

(t)], x

(0) = x

, t ≥ 0, (9.23)

NonlinearBook10pt November 20, 2007

562 CHAPTER 9

˙x

(t) = −

(t) −

(t)(1 + x

(t)) − x

(t), x

(0) = x

(9.24)

˙x

(t) = u(t), x

(0) = x

, (9.25)

where σ > 0. Once again, we seek a globally stabilizing controller for (9.23)–

(9.25) using Proposition 9.1. Note that (9.23)–(9.25) has the correct form

for the application of Proposition 9.1 where (9.23) and (9.24) make up the

nonlinear subsystem and x

is the integrator state. Speciﬁcally, (9.23)–(9.25)

can be written in the form of (9.1) and (9.2) where x = [x

]

, ˆx = x

and

f(x) =



(

+ 2x

+ x

)

−

(1 + x

)



, G(x) =



−1



To apply Proposition 9.1 we require a stabilizing feedback for the

subsystem (9.23) and (9.24) and a corresponding Lyapunov fun ction V

sub

(x)

such that (9.14)–(9.17) are satisﬁed. For the nonlinear subsystem (9.23) and

(9.24) we choose the Lyapunov function candidate

sub

(x) = εx

+ x

, (9.26)

where ε > 0, and the stabilizing feedback control

α(x) = −(2εσx

). (9.27)

It is straightforward to show that (9.26) and (9.27) s atisfy conditions (9.14)–

(9.17) of Proposition 9.1. Now, it f ollows from Proposition 9.1 that the

control law given by (9.13), that is,

u = −k(x

− α(x)) + P

−1

+ α

′

(x)[f(x) + G(x)x

], (9.28)

where k and P are positive constants, is a globally stabilizing feedback

control law for the overall system (9.23)–(9.25). △

Next, we consider the application of backsteppin g control design to

more general block cascade systems of the form

˙x(t) = f (x(t)) + G(x(t))ˆx(t), x(0) = x

, t ≥ 0, (9.29)

ˆx(t) =

f(x(t), ˆx(t)) +

G(x(t), ˆx(t))u(t), ˆx(0) = ˆx

, (9.30)

where the subsystem (9.29) is as (9.1) and ˆx ∈ R

f : R

× R

→ R

satisﬁes

f(0, 0) = 0, an d

G : R

×R

→ R

m×m

. Now, suppose det

G(x, ˆx) 6=

0, (x, ˆx) ∈ R

× R

, and suppose there exists a continuously diﬀerentiable

function α : R

→ R

such that the zero solution x(t) ≡ 0 of (9.29) is

asymptotically stable with ˆx replaced by α(x). In this case, it follows from

Theorem 3.9 that there exists a continuously diﬀerentiable positive-deﬁnite

function V

sub

: R

→ R such th at (9.17) holds. Now, once again using the

Lyapunov function candidate given by (9.10) for the overall system (9.29)

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 563

and (9.30), it follows that

V (x, ˆx) = V

′

sub

(x)[f(x) + G(x)α(x)] + V

′

sub

(x)G(x)[ˆx − α(x)]

+2[ˆx − α(x)]

f(x, ˆx) +

G(x, ˆx)u −α

′

(x)[f(x) + G(x)ˆx]

(9.31)

Now, choosing

u =

−1

(x, ˆx)



′

(x)[f(x) + G(x)ˆx] −

−1

(x)V

′T

sub

(x) −

f(x, ˆx)

−k(ˆx −α(x))



, (9.32)

where k > 0, it follows that (9.12) is satisﬁed, and hence, (9.32) stabilizes

the block cascade sy s tem (9.29) and (9.30). If, in addition, V

sub

(·) is radially

unbounded, (9.32) is a global stabilizer.

Using the b ackstepping f ormulation discussed above, it follows that a

recursive formulation of this approach can be used to stabilize strict-feedback

nonlinear smooth systems of the form

˙x(t) = f (x(t)) + G(x(t))ˆx

(t), x(0) = x

, t ≥ 0, (9.33)

ˆx

(t) =

(x(t), ˆx

(t)) +

(x(t), ˆx

(t))ˆx

(t), ˆx

(0) = ˆx

, (9.34)

ˆx

(t) =

(x(t), ˆx

(t), ˆx

(t)) +

(x(t), ˆx

(t), ˆx

(t))ˆx

(t),

ˆx

(0) = ˆx

, (9.35)

ˆx

(t) =

(x(t), ˆx

(t), . . . , ˆx

(t)) +

(x(t), ˆx

(t), . . . , ˆx

(t))u(t),

ˆx

(0) = ˆx

, (9.36)

where x ∈ R

, f : R

→ R

satisﬁes f(0) = 0, G : R

→ R

, ˆx

∈ R,

i = 1, . . . , m,

: R

× R

→ R satisﬁes

(0) = 0, i = 1, . . . , m, and

: R

× R

→ R, i = 1, . . . , m. Speciﬁcally, assuming

(x, ˆx

, . . . , ˆx

) 6=

0, 1 ≤ i ≤ m, and assuming the there exists an m-times continuously

diﬀerentiable fu nction α : R

→ R such that the ﬁrst subsystem (9.33) is

asymptotically stable with ˆx

replaced by α(x), a recursive backstepping

procedure can be used to stabilize (9.33)–(9.36).

In particular, considering th e system

˙x(t) = f(x(t)) + G(x(t))ˆx

(t), x(0) = x

, t ≥ 0, (9.37)

ˆx

(t) =

(x(t), ˆx

(t)) +

(x(t), ˆx

(t))ˆx

(t), ˆx

(0) = ˆx

, (9.38)

it follows from (9.29)–(9.32), with ˆx = ˆx

, u = ˆx

f(x, ˆx) =

(x, ˆx

), and

NonlinearBook10pt November 20, 2007

564 CHAPTER 9

G(x, ˆx) =

(x, ˆx

), that the feedback control law

(x, ˆx

) =

−1

(x, ˆx

)



′

(x)[f(x) + G(x)ˆx

] −

−1

(x)V

′T

sub

(x)

−

(x, ˆx

) − k

(ˆx

− α(x))



, k

> 0, (9.39)

asymptotically stabilizes (9.37) and (9.38) with Lyapu nov function

(x, ˆx

) = V

sub

(x) + P

(ˆx

− α(x))

, (9.40)

where V

sub

(x) is such that (9.3) holds. Next, considering the system

˙x(t) = f(x(t)) +

G(x(t))ˆx

(t), x(0) = x

, t ≥ 0, (9.41)

ˆx

(t) =

(x(t), ˆx

(t)) +

(x(t), ˆx

(t))ˆx

(t), ˆx

(0) = ˆx

, (9.42)

ˆx

(t) =

(x(t), ˆx

(t), ˆx

(t)) +

(x(t), ˆx

(t), ˆx

(t))ˆx

(t), ˆx

(0) = ˆx

(9.43)

it follows fr om (9.29)–(9.32), with x =



ˆx



, ˆx = ˆx

, u = ˆx

f(x) =



f(x) + G(x)ˆx

(x, ˆx

)



, G(x) =



(x, ˆx

)



f(x, ˆx) =

(x, ˆx

, ˆx

), and

G(x, ˆx) =

(x, ˆx

, ˆx

), that the feedback

control law

(x, ˆx

, ˆx

) = G

−1

(x, ˆx

, ˆx

)



∂α

(x, ˆx

)

∂x



[f(x) + G(x)ˆx

]



∂(x, ˆx

)α

∂ˆx



[

(x, ˆx

) + G

(x, ˆx

)ˆx

]

−

−1

(x, ˆx

)

∂V

(x, ˆx

)

∂ˆx

−

(x, ˆx

) − k

[ˆx

− α

(x, ˆx

)]



, k

> 0, (9.44)

asymptotically stabilizes (9.41)–(9.43) with Lyapunov function

(x, ˆx

, ˆx

) = V

(x, ˆx

) + P

(ˆx

− α

(x, ˆx

))

. (9.45)

Repeating this procedure m-times, an overall state feedback controller of

the form u = α

(x, ˆx

, . . . , ˆx

) with Lyapunov f unction V

(x, ˆx

, . . . , ˆx

)

can be obtained for the strict-feedback nonlinear system (9.34)–(9.36).

Example 9.3. To demonstrate the recursive backstepping procedure

discussed above consider the nonlinear dynamical system

˙x

(t) = x

(t) −x

(t) + x

(t), x

(0) = x

, t ≥ 0, (9.46)

˙x

(t) = x

(t), x

(0) = x

, (9.47)