Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 585

translated to the origin, it follows that the trans lated nonlinear system is

given by

˙x

(t) =

(t)(1 − (x

(t) + λ)

−

(t)), x

(0) = x

, t ≥ 0, (9.195)

˙x

(t) = −

−

λx

−

(λ

− 1 +

−

λx

− x

, x

(0) = x

(9.196)

˙x

(t) = −u(t), x

(0) = x

, (9.197)

where λ

△

= Φ

Teq

and u =

(Φ

−λ − x

Our objective is to stabilize the equilibrium (A(t) = 0, Φ(t) = 1,

Ψ(t) = Ψ

+2) by controlling the thr ottle mass ﬂow Φ

which is related to

the throttle opening γ

throt

by Φ

= γ

throt

√

Ψ [247]. To translate the desired

equilibrium to the origin we apply the linear transformation Φ

△

= Φ −1 and

△

= Ψ − Ψ

−2. Furthermore, in this case,

u =

(Φ

− 1 − Φ

), (9.198)

and h en ce, with λ = 1, (9.195)–(9.197) yield the transformed nonlinear

system

A(t) = −

A(t)[

(t) + 2Φ

(t) + Φ

(t)], A(0) = A

, t ≥ 0, (9.199)

(t) = −

(t) −

(t)[1 + Φ

(t)] − Ψ

(t), Φ

(0) = Φ

(9.200)

(t) = −u(t), Ψ

(0) = Ψ

. (9.201)

Note th at (9.199)–(9.201) has the correct form for the application of

Theorem 9.1 where (9.199) and (9.200) make up the nonlinear subsystem

and Ψ

is the integrator state. Speciﬁcally, (9.199)–(9.201) can be written

in the form of (9.1) and (9.2) where x = [A Φ

]

, ˆx = Ψ

, and

f(A, Φ

) =



−

+ 2Φ

+ Φ

)

−Φ

(

) −



, G(A, Φ

) =



−1



To apply Theorem 9.1 we require a stabilizing feedback for the

subsystem (9.199) and (9.200) and a corresponding Lyapunov function

sub

(A, Φ

) such that (9.59) and (9.60) are satisﬁed. For the nonlinear

subsystem (9.199) and (9.200) we choose the Lyapunov function candidate

sub

(A, Φ

) = εA

+ Φ

, (9.202)

where ε > 0, and the stabilizing feedback control

α(A, Φ

) = c

−

− 2εσA

, (9.203)

where c

≥ 0. I t is straightforward to show that (9.202) and (9.203) satisfy

conditions (9.59)–(9.61) of Theorem 9.1.

NonlinearBook10pt November 20, 2007

586 CHAPTER 9

Applying Theorem 9.1 to the system (9.199)–(9.201) yields the family

of control laws

u = −φ(A, Φ

, Ψ

) = R

−1

P (Ψ

− α(A, Φ

)) +

(A, Φ

, Ψ

)

, (9.204)

with Lyapunov fun ction

V (A, Φ

, Ψ

) = εA

+ Φ

P [Ψ

− α(A, Φ

)]

, (9.205)

where R

> 0 and

P > 0. Fu rthermore, the performance functional

minimized by the control law (9.204) has the form

J(A

, Φ

, Ψ

, u) =

∞

(A(t), Φ

(t), Ψ

(t))

(A(t), Φ

(t), Ψ

(t))u(t) + R

(t)]dt, (9.206)

where

(A, Φ

, Ψ

)

△

= R

(A, Φ

, Ψ

) − V

′

sub

(A, Φ

)[f(A, Φ

) + G(A, Φ

)Ψ

]

+2[Ψ

− α(A, Φ

)]

P α

′

(A, Φ

)[f(A, Φ

) + G(A, Φ

)Ψ

(9.207)

Now L

(A, Φ

, Ψ

) must be chosen to satisfy condition (9.62) or, equivalently,

(Ψ

− α(A, Φ

))



− 2Φ

− 2

′

(A, Φ

)(f(A, Φ

) + G(A, Φ

)Ψ

)

−1

[

P (Ψ

− α(A, Φ

)) +

(A, Φ

, Ψ

)]



< 0. (9.208)

A particular admissible choice for L

(A, Φ

, Ψ

) satisfying (9.208) is

given by

(A, Φ

, Ψ

) = −2R

{

−1

+ α

′

(A, Φ

)[f(A, Φ

) + G(A, Φ

)Ψ

]

−c

[Ψ

−α(A, Φ

)]}, (9.209)

where c

≥ 0. For this choice of L

(A, Φ

, Ψ

) the feedback control (9.204)

becomes

−φ(A, Φ

, Ψ

) = R

−1

P [Ψ

− α(A, Φ

)] −

−1

− α

′

(A, Φ

)[f(A, Φ

)

+G(A, Φ

)Ψ

] + c

(Ψ

− α(A, Φ

)), (9.210)

so that (9.208) satisﬁes

−2R

−1

(Ψ

− α(A, Φ

))

− c

P A

(Ψ

− α(A, Φ

))

< 0,

(A, Φ

, Ψ

) 6= (0, 0, 0). (9.211)

Note that instead of using L

(A, Φ

, Ψ

) to simply cancel the indeﬁnite

terms in (9.208), we have also added an extra term in which the stall cell

squared amplitude A

is multiplied by the tracking error Ψ

−α(A, Φ

) and a

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 587

nonnegative constant c

. This illustrates the ﬂexibility available in choosing

(A, Φ

, Ψ

) in the control law. In the special case

P =

, ε = 0, c

= 0,

and R

= 1/c

this control law specializes to the controller given in [247].

However, when ε vanishes the positive deﬁniteness of the Lyapunov fu nction

(9.205) over the whole state space is destroyed, and hence, the optimality

claims of Theorem 9.1 cannot be made for the controller given in [247].

Whereas by varying ε, c

, and

P in the control law (9.210), we can generate

a family of controllers w hich guarantee global asymptotic stability and global

optimality with respect to the performance functional (9.206).

Using the initial conditions A

= 0.5, Φ

= 0, Ψ

= 0, and parameter

values Ψ

= 0.72, σ = 3.6, β = 0.356, with

P = 2.5, R

= 1, ε = 0.0625,

and c

= 0.25 the inverse optimal control law (9.210) and the controller

given in [247] (with c

= c

= 1) were used to compare the closed-loop

system response. The squared stall cell amplitude responses for the two

controllers are compared in Figure 9.4, the compressor ﬂ ow and pr essure

rise responses are compared in Figures 9.5 and 9.6, and the control eﬀorts

are compared in Figures 9.7 and 9.8. In Figure 9.9 a phase portrait is

given comparing the overall s y s tem state trajectories for the two controllers.

This comparison illustrates that the present framework allows the control

designer to improve both the state response and the control eﬀort using the

state weights of the Lyapunov function,

P and ε, and the control weight

of the performance functional, R

. Furthermore, the trade-oﬀ between

achievable state response and allowable control eﬀort is characterized by the

performance functional (9.206). Finally, Figure 9.10 shows the compressor

pressure-ﬂow performance map parameterized as a function of the throttle

opening which constitutes a coexistent set of stable and unstable equilibria.

The controlled globally s table equilibrium point (0, 1, 2.72) correspond s to

the m aximum pressur e performance for the given compressor speed.

9.7 Surge Control for Centrifugal Co mpressors

While the literature on modeling and control of compression systems

predominantly focuses on axial ﬂow compression systems, the research

literature on centrifugal ﬂow compression systems is rather limited in

comparison. Notable exceptions include [21,113,119,138,184,223,357] which

address mod eling and control of centrifugal compressors. In contrast to axial

ﬂow compression systems involving the aerodynamic instabilities of rotating

stall and surge, a common feature of [21, 113, 119, 138, 184, 223, 357] is the

realization that surge (and deep surge) is the pr ed omin ant aerodynamic

instability arising in centrifugal compression systems.

To address the problem of nonlinear stabilization for centrifugal

compression systems we consider the basic centrifugal compression sys tem

NonlinearBook10pt November 20, 2007

588 CHAPTER 9

Theorem 4.1

Backstepping

0 5 10 15 20 25 30

0.05

0.1

0.15

0.2

0.25

0.3

Time (sec)

Squared Stall Cell Amplitude

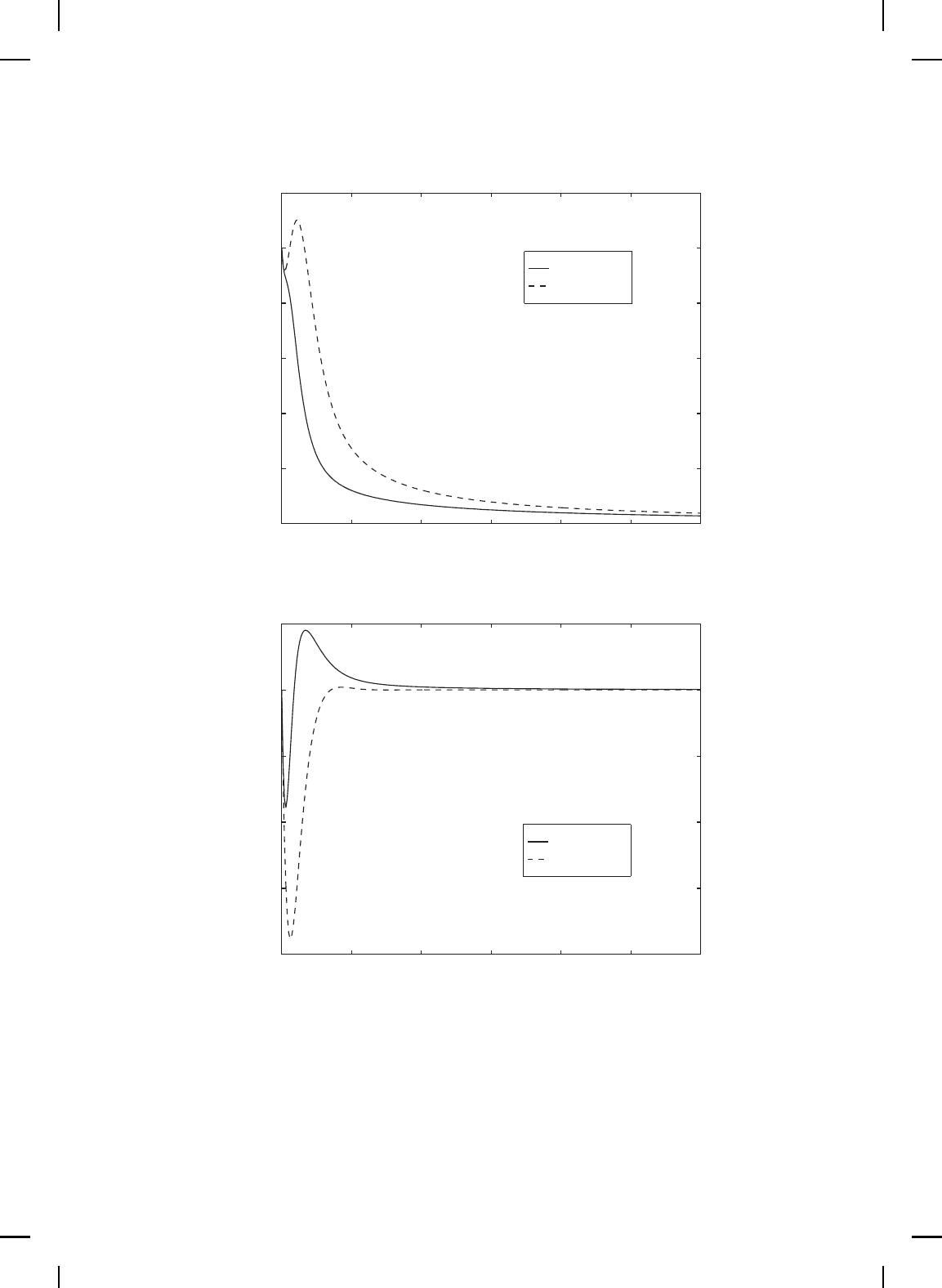
Figure 9.4 Squared stall cell amplitude versus time.

Theorem 4.1

Backstepping

0 5 10 15 20 25 30

0.8

0.85

0.9

0.95

1.05

Time (sec)

Compressor Flow

Figure 9.5 Compressor ﬂow versus time.

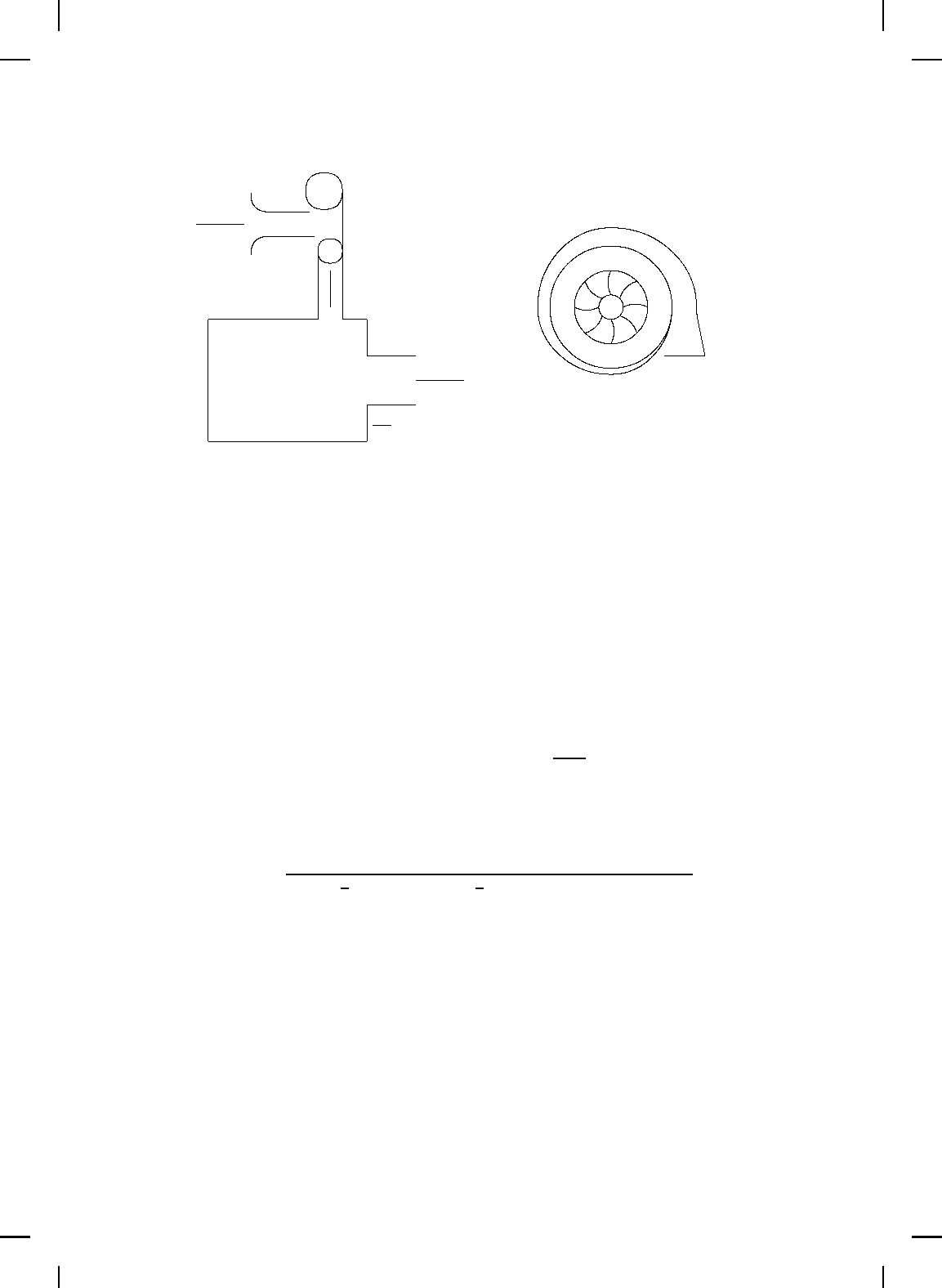
shown in Figure 9.11, consisting of a short inlet duct, a compressor, an

outlet duct, a plenum, an exit duct, and a control throttle. We assume

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 589

Theorem 4.1

Backstepping

0 5 10 15 20 25 30

1.8

1.9

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

Time (sec)

Pressure Rise in Compressor

Figure 9.6 Pressure rise versus time.

that the plenum d imen sions are large as compared to the compressor-duct

dimensions so that the ﬂuid velocity and acceleration in the plenum are

negligible. In this case, the pressure in the plenum is spatially uniform.

Furth ermore, we assume that the ﬂow is controlled by a throttle at the

plenum exit. In addition, we assume a low-speed compression system with

oscillation frequencies much lower than the acoustic resonance frequencies

so that the ﬂow can be considered incompressible. However, we do assume

that the gas in the plenum is compressible and acts as a gas spring. Finally,

we assume isentropic process dynamics in the plenum an d negligible gas

angular momentum in the compressor passages as compared to the impeller

angular momentum.

To address the problem of nonlinear stabilization for centrifugal

compression systems we use th e three-state lumped parameter mod el

for surge in centrifugal ﬂow compression systems developed in [119, 138,

278]. Speciﬁcally, pressure and mass ﬂow compression system dynamics

are developed u s ing principles of conservation of mass and momentum.

Furth ermore, in order to account for the inﬂuence of speed transients on

the compression surge dynamics, turbocharger spool dynamics are also

considered.

Using continuity it follows that mass conservation in the plenum is

NonlinearBook10pt November 20, 2007

590 CHAPTER 9

Theorem 4.1

Backstepping

0 5 10 15 20 25 30

0.8

0.9

1.1

1.2

1.3

1.4

Time (sec)

Throttle Flow

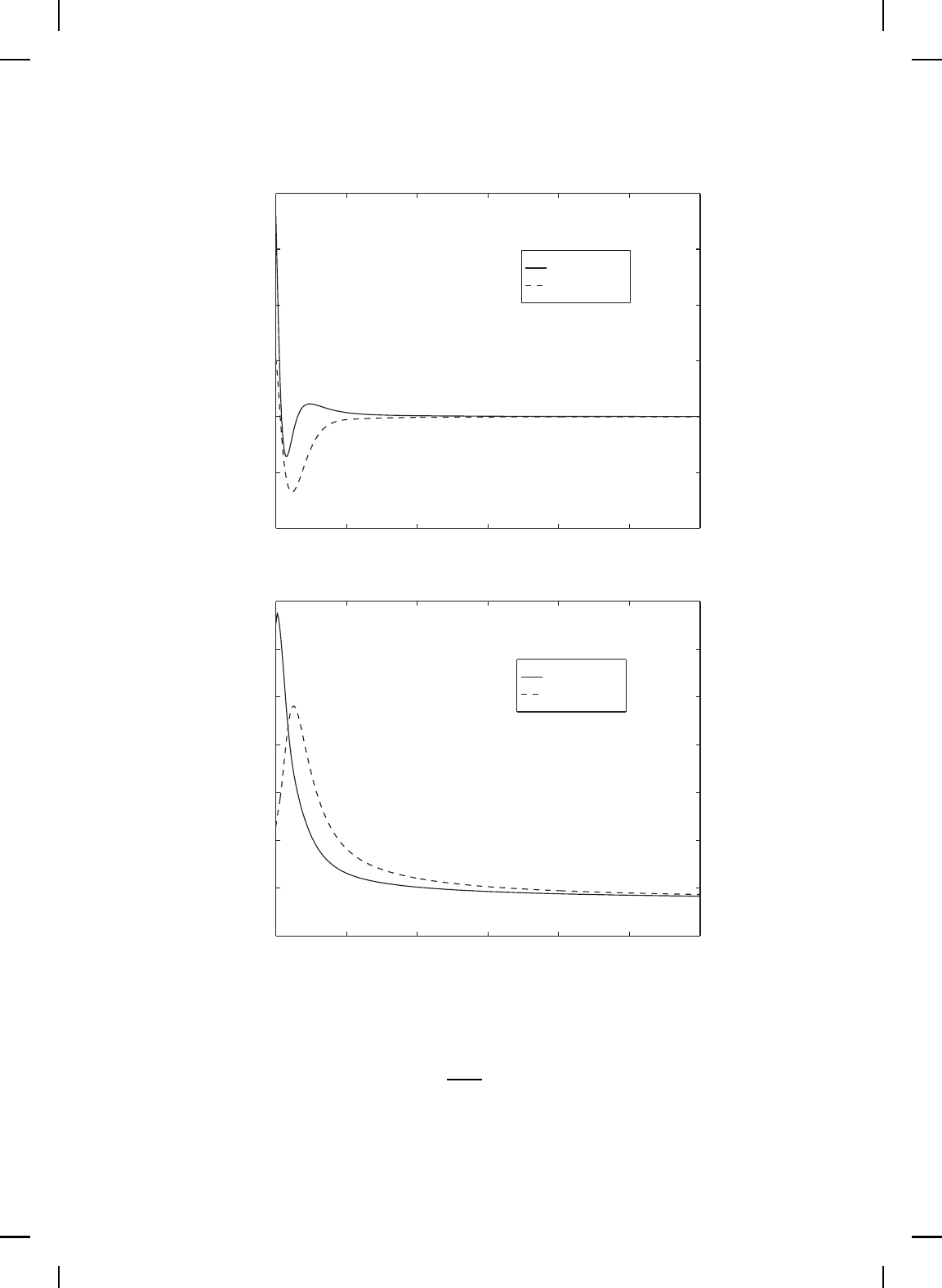
Figure 9.7 Throttle ﬂow versus time.

Theorem 4.1

Backstepping

0 5 10 15 20 25 30

1.4

1.5

1.6

1.7

1.8

1.9

2.1

Time (sec)

Throttle Opening

Figure 9.8 Throttle opening versus time.

given by

Ψ(t) = a(Φ(t) − γ

throt

Ψ(t)), Ψ(0) = Ψ

, t ≥ 0, (9.212)

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 591

Theorem 4.1

Backstepping

1.8

2.2

2.4

2.6

2.8

0.1

0.2

0.3

0.8

0.85

0.9

0.95

1.05

Figure 9.9 Phase portrait of state trajectories from (0.5, 1, 2.72)

Stable

Unstable

-1 -0.5 0 0.5 1 1.5 2

0.5

1.5

2.5

Compressor Flow

(Φ)

Pressure in Compressor (Ψ)

Figure 9.10 Compression system performance map.

where Φ is the nondimensional mass ﬂow rate at the plenum entrance, Ψ

is th e total-to-static pressure ratio, γ

throt

is a parameter proportional to

the throttle opening, and a is a nondimensional parameter r elated to the

compressor dimensions.

NonlinearBook10pt November 20, 2007

592 CHAPTER 9



















Compressor

Inlet Duct

Outlet Duct

Exit Duct

Throttle

Plenum



Outlet Diﬀuser





Vaneless Diﬀuser



*

Impeller

Volute





Figure 9.11 Centrifugal compressor system geometry.

Next, using a momentum balance with the assumption of incompress-

ible ﬂow, using the fact that the change in angular momentum of the ﬂuid is

equal to the compressor torque, assuming isentropic process dyn amics with

constant speciﬁc heat, and assuming an absence of prewhirl at the rotor

inlet, it follows that [107, 193,309]

Φ(t) = b(Ψ

(Φ(t), Ω(t)) −Ψ(t)), Φ(0) = Φ

, t ≥ 0, (9.213)

where Ω is th e n ondimensional angular velocity of compressor spool, Ψ

(Φ,

Ω) is the compressor characteristic pressure-ﬂow/angular velocity map given

(Φ, Ω)

△



1 + η

(Φ, Ω)σdΩ



−1

− 1, (9.214)

where γ

is the speciﬁc heat ratio and η

(Φ, Ω) is the isentropic eﬃciency

given by ([278])

(Φ, Ω)

△

σΩ

Ω − f

Φ)

(σΩ −f

Φ)

+ Φ

+ f

)

. (9.215)

Here, σ is the slip factor and b, d, f

, i = 1, . . . , 5, are nondimensional

parameters related to the compressor dimensions, the sound velocity in

the plenum, the indu cer and rotor geometry, and the friction coeﬃcients,

respectively.

It is important to note that the compressor characteristic map given by

(9.214) holds for the case where the ﬂow through the compressor is positive.

In the case of deep surge involving negative mass ﬂow, it is assumed that

the pressure rise in the compressor is proportional to the square of the mass

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 593

ﬂow so that [184]

(Φ, Ω) = µΦ

+ Ψ

(Φ, Ω), Φ < 0, (9.216)

where µ is a constant and

(Φ, Ω)

△

= Ψ

(Φ, Ω)



Φ=0

= (1 + ση

dΩ

)

−1

− 1, (9.217)

where

△

= η

(Φ, Ω)|

Φ=0

2σ

+ 2σ + f

. (9.218)

It is shown in [278] that η

max

is constant for all spool speeds.

This indicates th at the compressor achieves the same maximum isentropic

eﬃciency at each maximum p ressure point for all spool speeds. However,

since these points are critically stable, active control is needed to guarantee

stable compression system operation for peak compressor performance.

Figure 9.12 shows a typical family of compressor characteristic maps for

diﬀerent spool speeds along with the corresponding constant isentropic

eﬃciency lines. Th e stone wall depicted in Figure 9.12 corresponds to choked

ﬂow at a given cross-section of the compression system [138,278].

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0.6

0.7

0.8

0.9

0.8

0.7

0.6

0.55

0.45

0.4

0.35

0.3

Constant ω lines

Constant η lines

Max ψ line

Stone wall

Figure 9.12 Compressor characteristic maps and eﬃciency lines for diﬀerent spool speed s.

Finally, using conservation of angular momentum in the turbocharger

spool it follows that the nondimensional s pool dynamics are given by

Ω(t) = c(τ(t) −σΦ(t)Ω(t)), Ω(0) = Ω

, t ≥ 0, (9.219)

NonlinearBook10pt November 20, 2007

594 CHAPTER 9

where τ (·) is the nondimensional driving torque and c is a nondimensional

parameter related to th e spool mass moment of inertia.

Next, we apply th e inverse optimal backstepping control framework to

control surge in centrifugal compression systems. First, we note that with

control inputs u

△

= γ

throt

√

Ψ and u

△

= τ it follows fr om (9.212), (9.213),

and (9.219), that a state space model for the centrifugal compressor is given

Ψ(t) = a(Φ(t) − u

(t)), Ψ(0) = Ψ

, t ≥ 0, (9.220)

Φ(t) = b(Ψ

(Φ(t), Ω(t)) −Ψ(t)), Φ(0) = Φ

, (9.221)

Ω(t) = c(u

(t) −σΦ(t)Ω(t)), Ω(0) = Ω

. (9.222)

Note that for ﬁxed values of the control inputs u

and u

, (9.220), (9.221)

and (9.222) give an equilibrium point (Ψ

, Φ

, Ω

), where (Ψ

, Φ

, Ω

)

is given by

(Ψ

, Φ

, Ω

) =



(Φ

, Ω

), u

1eq

2eq

σΦ



. (9.223)

Deﬁning th e shifted state variables x

△

= Ψ − Ψ

, x

△

= Φ − Φ

, and

△

= Ω − Ω

, so that for a given equilibrium point on the compressor

characteristic map th e system equilibrium is translated to the origin, and

deﬁning the shifted controls ˜u

△

= u

− u

1eq

and ˜u

△

= u

− u

2eq

, it follows

that the translated n onlinear system is given by

˙x

(t) = a(x

(t) − ˜u

(t)), x

(0) = x

, t ≥ 0, (9.224)

˙x

(t) = b(Ψ

Ceq

(t), x

(t)) − x

(t)), x

(0) = x

, (9.225)

˙x

(t) = c(˜u

(t) −f(x

(t), x

(t))), x

(0) = x

, (9.226)

where

Ceq

, x

)

△

= Ψ

(Φ

+ x

, Ω

+ x

) − Ψ

(Φ

, Ω

), (9.227)

f(x

, x

)

△

= σ(Φ

+ Ω

) + σx

. (9.228)

Now, setting

ˆu = x

− ˜u

, (9.229)

˜u

= −k

+ f (x

, x

), (9.230)

where k

> 0, and substituting (9.229) and (9.230) into (9.224)–(9.226)

yields

˙x

(t) = aˆu(t), x

(0) = x

, t ≥ 0, (9.231)

˙x

(t) = b(Ψ

Ceq

(t), x

(t)) − x

(t)), x

(0) = x

, (9.232)

˙x

(t) = −k

(t), x

(0) = x

. (9.233)

Note th at (9.231)–(9.233) has the correct form for the application of