Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DISTURBANCE REJECTION CONTROL 615

from Lemma 10.1 that

V (x(T )) ≤

(t)w(t)dt, w(·) ∈ L

, T ≥ 0,

which yields (10.66).

10.4 A Riccati Equation Characterization for

Mixed H

Performance

In this section, we consider the dynamical system (10.1) and (10.2) with

f(x) = Ax, J

(x) = D, h(x) = Ex, and J

(x) = E

∞

, where A ∈ R

n×n

D ∈ R

n×d

, E ∈ R

p×n

, E

∞

∈ R

p×d

, and where A is asymptotically stable so

that

˙x(t) = Ax(t) + Dw(t), x(0) = 0, w(·) ∈ L

, t ≥ 0, (10.68)

z(t) = Ex(t) + E

∞

w(t), (10.69)

where

W consists of unit-peak input signals deﬁned by

△

= {w(·) : w

(t)w(t) ≤ 1, t ≥ 0}. (10.70)

The following result provides an upper bound to the L

norm [104] (L

∞

equi-

induced norm) of the convolution operator G of the linear, time-invariant

system (10.68) and (10.69) given by

|||G|||

△

= sup

w(·)∈L



sup

t≥0

kz(t)k



where k · k denotes the Euclidean vector norm. From an input-output

point of view the L

norm captures the worst-case ampliﬁcation from input

disturbance signals to output signals, where the signal size is taken to be

the supremum over time of th e signal’s pointwise-in-time Euclidean norm.

Theorem 10.3. Let α > 0 and consider the linear dynamical system

(10.68) and (10.69). Then

|||G|||

≤ σ

1/2

max

(EP

−1

) + σ

1/2

max

∞

), (10.71)

where P > 0 satisﬁes

0 ≥ A

P + P A + αP +

P DD

P. (10.72)

Proof. Let T ≥ 0 and consider the shifted linear d ynamical system

˜x(t) = A

˜x(t) + Dv(t), ˜x(0) = 0, t ≥ 0, (10.73)

z(t) = e

−

(t−T )

(E˜x(t) + E

∞

v(t)), (10.74)

NonlinearBook10pt November 20, 2007

616 CHAPTER 10

where A

△

= A+

I, α > 0, ˜x(t)

△

= e

(t−T )

x(t), and v(t)

△

= e

(t−T )

w(t). Note

that (10.73) and (10.74) are equivalent to (10.68) and (10.69). Furthermore,

note that if w(·) ∈

W then v(·) ∈ V, where V

△

= {v(·) :

(t)v(t)dt ≤

Hence,

|||G|||

≤ sup

T ≥0

sup

v(·)∈V

kz(T )k

Next, with f(x) = A

˜x(t), J

(x) = D, V (x) = ˜x

P ˜x, W = V, β =

γ = 1, and L(x) = ˜x

R˜x, where R ∈ R

n×n

is an arbitrary positive-deﬁnite

matrix, it follows from Theorem 10.2 that if there exists P > 0 such that

0 = A

P + P A

P DD

P + R, (10.75)

then

˜x

(T )P ˜x(T ) ≤ 1,

and h en ce, for all v(·) ∈ V,

kz(T )k = kE˜x(T ) + E

∞

w(T )k ≤ σ

1/2

max

(EP

−1

) + σ

1/2

max

∞

The result is now immediate by noting that (10.75) is equivalent to (10.72).

Note that we can replace the Riccati inequality (10.72) by the Riccati

equation

0 = A

P + P A + αP +

P DD

P (10.76)

in Theorem 10.3. In this case, if (A, D) is controllable and A

asymptotically stable, then there exists a positive-deﬁnite solution satisfying

(10.76). In particular,

P =



∞



−1

. (10.77)

Now, letting Q = αP

−1

in Theorem 10.3 yields

|||G|||

≤

1/2

max

(EQE

) + σ

1/2

max

∞

), (10.78)

where Q > 0 satisﬁes

0 ≥ AQ + QA

+ αQ + DD

. (10.79)

Furth ermore, it is interesting to note that in the case where E

∞

= 0 the

solution Q to (10.79) satisﬁes the bound

Q ≤ Q, (10.80)

where Q satisﬁes

0 = AQ + QA

+ DD

, (10.81)

NonlinearBook10pt November 20, 2007

DISTURBANCE REJECTION CONTROL 617

and h en ce,

|||G|||

= tr EQE

≤ tr EQE

. (10.82)

Thus , (10.79) can be used to provide a trade-oﬀ between H

and mixed

performance. For further details see [157].

10.5 Nonlinear-Nonquadratic Controllers for Systems with

Bounded Disturbances

In this section, we consider a control problem involving a notion of optimality

with respect to an auxiliary cost which guarantees a bound on th e worst-case

value of a nonlinear-nonquadratic cost functional over a prescribed set of

bounded input disturbances. The optimal feedback controllers are derived

as a direct consequence of Theorem 10.1 and provide a generalization of

the Hamilton-Jacobi-Bellman conditions for time-invariant, inﬁnite-horizon

problems for addressing nonlinear feedback controllers for nonlinear systems

with bounded energy disturbances th at additionally minimize a nonlinear-

nonquadratic cost functional.

To address the optimal control problem let D ⊂ R

be an open set

and let U ⊂ R

, where 0 ∈ D and 0 ∈ U. Furthermore, let W ⊂ R

and

let r : R

× R

→ R be a given f unction. Next, consider the controlled

dynamical system

˙x(t) = F (x(t), u(t)) + J

(x(t))w(t) x(0) = x

, w(·) ∈ L

, t ≥ 0,

(10.83)

with performance variables

z(t) = h(x(t), u(t)) + J

(x(t))w(t), (10.84)

where F : R

×R

→ R

satisﬁes F (0, 0) = 0, J

: R

→ R

, h : R

×R

→

satisﬁes h(0, 0) = 0, J

: R

→ R

p×d

, and the control u(·) is restricted to

the class of admissible controls consisting of measurab le functions u(·) ∈ U

such that u(t) ∈ U for all t ≥ 0, where th e control constraint set U is given.

We assume 0 ∈ U. Given a control law φ(·) and a feedback control law

u(t) = φ(x(t)), the closed-loop system shown in Figure 10.1 has th e form

˙x(t) = F (x(t), φ(x(t))) + J

(x(t))w(t), x(0) = x

, t ≥ 0, (10.85)

z(t) = h(x(t), φ(x(t))) + J

(x(t))w(t). (10.86)

We assume that the mapping φ : D → U satisﬁes suﬃcient regularity

conditions such that the resulting closed-loop system (10.85) has a unique

solution forward in time.

Next, we present an extension of Theorem 8.2 for characterizing

feedback controllers that guarantee stability, minimize an auxiliary perfor-

mance functional, and guarantee that the input-output map of the closed-

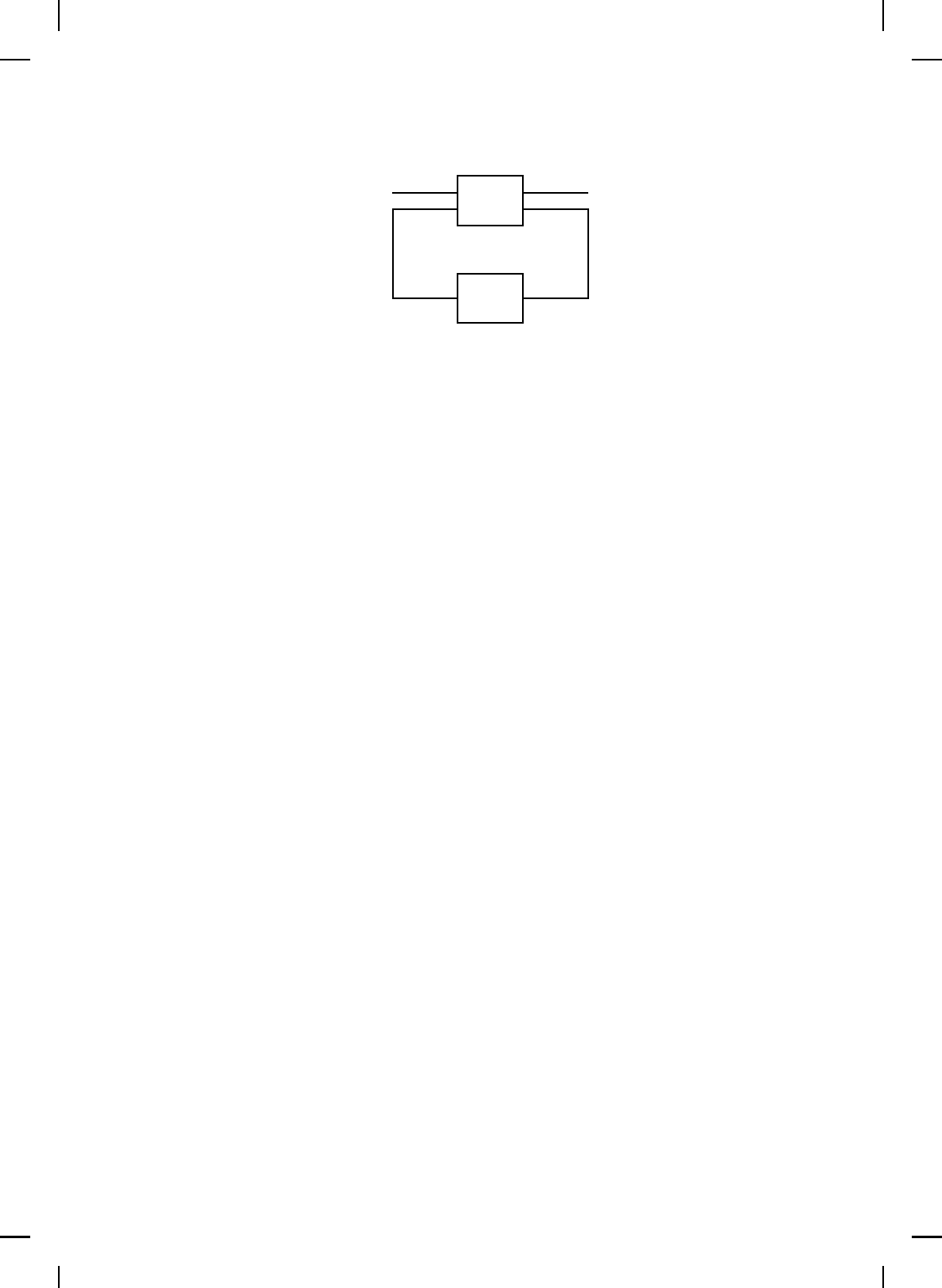
NonlinearBook10pt November 20, 2007

618 CHAPTER 10

φ(x)

- -

w z



Figure 10.1 Disturbed nonlinear closed-loop feedback system.

loop system is dissipative, nonexpan s ive, or passive for bounded input

disturbances. For the statement of these results let L : D × U → R and

deﬁne the set of regulation controllers for the nonlinear system with w(t) ≡ 0

S(x

)

△

= {u(·) : u(·) is admissible and x(·) given by (10.83)

satisﬁes x(t) → 0 as t → ∞ with w(t) ≡ 0}.

Theorem 10.4. Consider the nonlinear controlled dynamical system

(10.83) and (10.84) with performance functional

J(x

, u(·))

△

∞

L(x(t), u(t))dt, (10.87)

where u(·) is an admissible control. Assume that there exist a continuously

diﬀerentiable function V : D → R, a function Γ : D × U → R, and control

law φ : D → U s uch that

V (0) = 0, (10.88)

V (x) > 0, x ∈ D, x 6= 0, (10.89)

φ(0) = 0, (10.90)

′

(x)F (x, φ(x)) < 0, x ∈ D, x 6= 0, (10.91)

′

(x)J

(x)w ≤ r(z, w) + L(x, φ(x)) + Γ(x, φ(x)), x ∈ D, w ∈ W,

(10.92)

H(x, φ(x)) = 0, x ∈ D, (10.93)

H(x, u) ≥ 0, x ∈ D, u ∈ U, (10.94)

where

H(x, u)

△

= V

′

(x)F (x, u) + L(x, u) + Γ(x, u). (10.95)

Then, with the feedback control u(·) = φ(x(·)), there exists a neighborhood

⊆ D of the origin such that if x

∈ D

and w(t) ≡ 0, the zero solution

x(t) ≡ 0 of the closed-loop system (10.85) is locally asymptotically stable.

If, in addition, Γ(x, φ(x)) ≥ 0, x ∈ D, then

J(x

, φ(x(·))) ≤ J(x

, φ(x(·))) = V (x

), (10.96)

NonlinearBook10pt November 20, 2007

DISTURBANCE REJECTION CONTROL 619

where

J(x

, u(·))

△

∞

[L(x(t), u(t)) + Γ(x(t), u(t))]dt (10.97)

and where u(·) is admissible and x(t), t ≥ 0, solves (10.83) with w(t) ≡ 0.

In addition, if x

∈ D

then the feedback control u(·) = φ(x(·)) minimizes

J(x

, u(·)) in the sense th at

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)). (10.98)

Furth ermore, the solution x(t), t ≥ 0, of (10.85) satisﬁes the dissipativity

constraint

r(z(t), w(t)) + V (x

) ≥ 0, w(·) ∈ L

, T ≥ 0. (10.99)

Finally, if D = R

, U = R

, w(t) ≡ 0, and

V (x) → ∞ as kxk → ∞, (10.100)

then the zero solution x(t) ≡ 0 of the closed-loop system (10.85) is globally

asymptotically stable.

Proof. Local and global asymptotic stability is a direct consequence of

(10.88)–(10.91) by applying Theorem 10.1 to the closed-loop system (10.85).

Furth ermore, using (10.93), the performance bound (10.96) is a restatement

of (10.17) as applied to the closed-loop system. Next, let u(·) ∈ S(x

) and

let x(t), t ≥ 0, be the solution of (10.83) with w(t) ≡ 0. Then (10.98)

follows from Theorem 8.2 with L(x, u) replaced by L(x, u) + Γ(x, u) and

J(x

, u(·)) replaced by J(x

, u(·)). Finally, using (10.92), condition (10.99)

is a restatement of (10.19) as app lied to th e closed-loop system.

Next, we specialize Theorem 10.4 to linear systems w ith bounded

energy disturbances and provide connections to the m ixed-norm H

∞

and mixed H

/positivity frameworks developed in [49] and [146, 420],

respectively. Speciﬁcally, we consider the case in which F (x, u) = Ax + Bu,

(x) = D, h(x, u) = E

x + E

u, and J

(x) = E

∞

, where A ∈ R

n×n

B ∈ R

n×m

, D ∈ R

n×d

, E

∈ R

p×n

, E

∈ R

p×m

, and E

∞

∈ R

p×d

. First,

we consider the mixed-norm H

∞

case where r(z, w) = γ

w − z

and where γ > 0 is given. For the following result deﬁne R

△

= E

> 0,

△

= E

> 0, S

△

= BR

−1

, and assume E

∞

= 0 and R

△

= E

= 0.

Corollary 10.3. Consider the linear controlled system

˙x(t) = Ax(t) + Bu(t) + Dw(t), x(0) = x

, w(·) ∈ L

, t ≥ 0, (10.101)

z(t) = E

x(t) + E

u(t), (10.102)

NonlinearBook10pt November 20, 2007

620 CHAPTER 10

with performance functional

J(x

, u(·)) =

∞

(t)R

x(t) + u

u(t)]dt, (10.103)

where u(·) is admissib le. Assume th at there exists a positive-deﬁnite matrix

P ∈ R

n×n

such that

0 = A

P + P A + R

+ γ

−2

P DD

P − P SP, (10.104)

where γ > 0. Then, with the feedback control law u = φ(x) = −R

−1

P x,

the zero solution x(t) ≡ 0 of th e u ndisturbed (w(t) ≡ 0) system (10.101) is

globally asymptotically stable for all x

∈ R

and

J(x

, φ(x(·))) ≤ J(x

, φ(x(·))) = x

P x

, (10.105)

where

J(x

, u(·)) =

∞

(t)(R

+γ

−2

P DD

P )x(t)+u

(t)R

u(t)]dt, (10.106)

and where u(·) is adm iss ible and x(t), t ≥ 0, s olves (10.101) with w(t) ≡ 0.

Furth ermore,

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), (10.107)

where S(x

) is the set of regulation controllers for the system (10.101) with

w(t) ≡ 0 and x

∈ R

. Finally, if x

= 0 then, with u = φ(x), the solution

x(t), t ≥ 0, of (10.101) satisﬁes the nonexpansivity constraint

z(t)

z(t)dt ≤ γ

w(t)

w(t)dt, w(·) ∈ L

, T ≥ 0, (10.108)

or, equivalently, |||

G(s)|||

∞

≤ γ, where

G(s) ∼



A + BK D

+ E

K 0



and K

△

= −R

−1

P .

Proof. The result is a direct consequ en ce of Theorem 10.4 with

F (x, u) = Ax + Bu, J

(x) = D, L(x, u) = x

x + u

u, V (x) =

P x, Γ(x, u) = γ

−2

P DD

P x, D = R

, and U = R

. Speciﬁcally,

conditions (10.88)–(10.91) are trivially satisﬁed. Now, forming x

(10.104)x

it follows that, after some algebraic manipulations, V

′

(x)J

(x)w ≤ r(z, w)+

L(x, φ(x), w) + Γ(x, φ(x), w), for all x ∈ D and w ∈ W. Furthermore,

it follows from (10.104) that H(x, φ(x)) = 0 and H(x, u) = H(x, u) −

H(x, φ(x)) = [u −φ(x)]

[u −φ(x)] ≥ 0 so that all conditions of Theorem

10.4 are satisﬁed. Finally, since V (·) is radially unbounded, (10.101), with

u(t) = φ(x(t)) = −R

−1

P x(t), is globally asymptotically s table.

NonlinearBook10pt November 20, 2007

DISTURBANCE REJECTION CONTROL 621

In the case where U = R

the feedback control u = φ(x) is globally

optimal since it minimizes H(x, u) and satisﬁes (10.93). Speciﬁcally, setting

∂

∂u

H(x, u) = 0, (10.109)

yields the feedback control

φ(x) = −R

−1

P x. (10.110)

Now, since

∂

∂u

H(x, u) = R

> 0, (10.111)

it follows that f or all x ∈ R

the feedback control given by (10.110) minimizes

H(x, u). In particular, the optimal feedback control law φ(x) in Corollary

10.3 is derived us ing the properties of H(x, u) as deﬁned in Th eorem 10.4.

Speciﬁcally, since H(x, u) = x

P +P A+R

+γ

−2

P DD

P )x+u

P Bu it follows that ∂

H/∂u

> 0. Now, ∂H/∂u = 2R

u + 2B

P x = 0

gives the unique global minimum of H(x, u). Hence, since φ(x) minimizes

H(x, u) it follows that φ(x) s atisﬁes ∂H/∂u = 0 or, equivalently, R

φ(x) +

P x = 0 so that φ(x) is given by (10.110). Similar remarks hold for the

controllers developed in Corollary 10.4 and Section 10.8.

Next, we specialize Theorem 10.4 to provide connections to the mixed

/positivity framework developed in [146, 420]. Speciﬁcally, we consider

the case where p = d and r(z, w) = 2w

z. For the following result

deﬁne R

△

= (E

∞

+ E

∞

)

−1

, R

△

= R

+ E

, R

△

= E

(I + R

−

−1

, B

△

= B − DR

, A

△

= A − (B

−1

+ D)R

and S

△

= B

−1

. Furthermore, assume that E

> 0 and E

> 0.

Note that using S chur complements it can be shown that R

> 0.

Corollary 10.4. Consid er the linear dynamical s ystem (10.101) with

performance variables

z(t) = E

x(t) + E

u(t) + E

∞

w(t) (10.112)

and performance functional (10.103). Assume that there exists a positive-

deﬁnite matrix P ∈ R

n×n

such that

0 = A

P + P A

+ R

+ P DR

P − P S

P. (10.113)

Then, with the feedback control law u = φ(x) = −R

−1

P + E

)x,

the zero solution x(t) ≡ 0 of th e undistur bed (w(t) ≡ 0) system (10.101) is

globally asymptotically stable for all x

∈ R

and

J(x

, φ(x(·))) ≤ J(x

, φ(x(·))) = x

P x

, (10.114)

NonlinearBook10pt November 20, 2007

622 CHAPTER 10

where

J(x

, u(·)) =

∞

(t)(R

+ (D

P − E

)

P − E

))x(t)

(t)R

u(t) −2x

(t)(D

P − E

)

u(t)]dt

(10.115)

and where u(·) is adm iss ible and x(t), t ≥ 0, s olves (10.101) with w(t) ≡ 0.

Furth ermore,

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), (10.116)

where S(x

) is the set of regulation controllers for the system (10.101) with

w(t) ≡ 0 and x

∈ R

. Finally, if x

= 0, then, with u = φ(x), the solution

x(t), t ≥ 0, of (10.101) satisﬁes the passivity constraint

(t)z(t) ≥ 0, w(·) ∈ L

, T ≥ 0, (10.117)

or, equivalently,

∞

(s) +

∗

∞

(s) ≥ 0, Re[s] > 0, where

∞

(s) ∼



A + BK D

+ E

K E

∞



and K = −R

−1

P + E

Proof. The result is a direct consequ en ce of Theorem 10.4 with

F (x, u) = Ax + Bu, J

(x) = D, L(x, u) = x

x + u

u, V (x) = x

P x,

Γ(x, u) = [(D

P − E

)x − E

[(D

P − E

)x − E

u], D = R

, and

U = R

. Speciﬁcally, conditions (10.88)–(10.91) are trivially satisﬁed. Now,

forming x

(10.113)x it follows that, after some algebraic manipulations,

′

(x)J

(x)w ≤ r(z, w) + L(x, φ(x), w) + Γ(x, φ(x), w), for all x ∈ D and

w ∈ W. Furthermore, it follows from (10.113) that H(x, φ(x)) = 0 an d

H(x, u) = H(x, u) − H(x, φ(x)) = [u − φ(x)]

[u − φ(x)] ≥ 0 so that

all conditions of Theorem 10.4 are satisﬁed. Finally, since V (x) is radially

unbounded, (10.101), with u(t) = φ(x(t)) = −R

−1

P + E

)x(t), is

globally asymptotically stable.

10.6 Optimal and Inverse Optimal Control for Aﬃne Systems

with L

Disturbances

In this section, we specialize Theorem 10.4 to aﬃne (in the control) systems

of the form

˙x(t) = f(x(t)) + G(x(t))u(t) + J

(x(t))w(t), x(0) = x

, w(·) ∈ L

, t ≥ 0,

(10.118)

NonlinearBook10pt November 20, 2007

DISTURBANCE REJECTION CONTROL 623

with performance variables

z(t) = h(x(t)) + J(x(t))u(t), (10.119)

where f : R

→ R

satisﬁes f(0) = 0, G : R

→ R

n×m

, J : R

→ R

p×m

h : R

→ R

satisﬁes h(0) = 0, D = R

, and U = R

. First, we consider

the nonexpansivity case so that the supply rate r(z, w) is given by r(z, w) =

w−z

z, where γ > 0. For the following result, we consider performance

integrands L(x, u) of the form

L(x, u) = [h(x) + J(x)u]

[h(x) + J(x)u], (10.120)

where J

(x)J(x) > 0, x ∈ R

, so that (10.87) becomes

J(x

, u(·)) =

∞

[h(x(t)) + J(x(t))u(t)]

[h(x(t)) + J(x(t))u(t)]dt.

(10.121)

Corollary 10.5. Consid er the nonlinear controlled dynamical system

(10.118) and (10.119) with perform ance fun ctional (10.121). Assume that

there exists a continuously diﬀerentiable function V : R

→ R such that

V (0) = 0, (10.122)

V (x) > 0, x ∈ R

, x 6= 0, (10.123)

′

(x)[f(x) −

G(x)R

−1

(x)(V

′

(x)G(x) + 2h

(x)J(x))

] < 0,

x ∈ R

, x 6= 0, (10.124)

0 = V

′

(x)f(x) + h

(x)h(x) +

4γ

′

(x)J

(x)V

′T

(x)

−

′

(x)G(x) + 2h

(x)J(x)]R

−1

(x)[V

′

(x)G(x) + 2h

(x)J(x)]

, x ∈ R

(10.125)

and

V (x) → ∞ as kxk → ∞, (10.126)

where γ > 0 and R

(x)

△

= J

(x)J(x). Then the zero solution x(t) ≡ 0 of

the undisturbed (w(t) ≡ 0) closed-loop system

˙x(t) = f (x(t)) + G(x(t))φ(x(t)), x(0) = x

, t ≥ 0, (10.127)

is globally asymptotically stable with feedback control law

φ(x) = −

−1

(x)[V

′

(x)G(x) + 2h

(x)J(x)]

. (10.128)

Furth ermore, the performance functional (10.121) satisﬁes

J(x

, φ(x(·))) ≤ J(x

, φ(x(·))) = V (x

), (10.129)

where

J(x

, u(·))

△

∞

[L(x(t), u(t)) + Γ(x(t), u(t))]dt, (10.130)

NonlinearBook10pt November 20, 2007

624 CHAPTER 10

Γ(x, u) =

4γ

′

(x)J

(x)V

′T

(x). (10.131)

In addition, the performance functional (10.130) is minimized in the sense

that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)). (10.132)

Finally, with u(·) = φ(x(·)), the solution x(t), t ≥ 0, of the closed-loop

system (10.118) satisﬁes the nonexpansivity constraint

(t)z(t)dt ≤ γ

(t)w(t)dt + V (x

), T ≥ 0, w(·) ∈ L

(10.133)

Proof. The result is a direct consequ en ce of Theorem 10.4 with

F (x, u) = f (x) + G(x)u, z = h(x)+ J(x)u, L(x, u) = [h(x) + J(x)u]

[h(x)+

J(x)u], J

(x) = 0, Γ(x, u) given by (10.131), D = R

, and U = R

Speciﬁcally, with (10.120) and (10.131), the Hamiltonian has the form

H(x, u) = [h(x) + J(x)u]

[h(x) + J(x)u] + V

′

(x)(f(x) + G(x)u)

4γ

′

(x)J

(x)V

′T

(x).

Now, the feedback control law (10.128) is obtained by setting

∂H

∂u

= 0.

With (10.128), it follows that (10.122)–(10.124) imply (10.88), (10.89), and

(10.91). Next, since V (·) is continuously diﬀerentiable and x = 0 is a local

minimum of V (·), it follows that V

′

(0) = 0, and hence, since by assumption

h(0) = 0, it follows that φ(0) = 0, which proves (10.90). Next, with φ(x)

given by (10.128), it follows from (10.125) that (10.93) h olds. Finally, since

H(x, u) = H(x, u) − H(x, φ(x)) = [u − φ(x)]

(x)[u − φ(x)], and R

(x)

is positive deﬁnite for all x ∈ R

, condition (10.94) holds. The result now

follows as a direct consequence of Theorem 10.4.

Next, we consider performance integrands L(x, u) of the f orm

L(x, u) = L

(x) + L

(x)u + u

(x)u, (10.134)

where L

: R

→ R, L

: R

→ R

1×m

, and R

: R

→ P

so that (10.87)

becomes

J(x

, u(·)) =

∞

(x(t)) + L

(x(t))u(t) + u

(t)R

(x)u(t)]dt. (10.135)

Corollary 10.6. Consider the nonlinear controlled dynamical system

(10.118) and (10.119) with perform ance functional (10.135). Assume that

there exist a continuously diﬀerentiable function V : R

→ R and a function

: R

→ R

1×m

such that

V (0) = 0, (10.136)

(0) = 0, (10.137)