Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach
Подождите немного. Документ загружается.


NonlinearBook10pt November 20, 2007
OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 595
Theorem 9.1 where (9.232) and (9.233) make up the nonlinear subsystem
and x
1
is the integrator state. Specifically, (9.231)–(9.233) can be written
in the form of (9.1) and (9.2) where x = [x
2
x
3
]
T
, ˆx = x
1
, and
f(x
2
, x
3
) =
bΨ
Ceq
(x
2
, x
3
)
−k
3
cx
3
, G(x
2
, x
3
) =
−b
0
.
To apply Theorem 9.1 we require a stabilizing feedback for the
subsystem (9.232) and (9.233) and a corresponding Lyapunov function
V
sub
(x
2
, x
3
) such that (9.59) and (9.60) are satisfied. For the nonlinear
subsystem (9.232) and (9.233) we choose the Lyapunov function candidate
V
sub
(x
2
, x
3
) =
1
2
α
2
x
2
2
+
1
2
α
3
x
2
3
, (9.234)
where α
2
, α
3
> 0, and the stabilizing feedback control
α(x
2
, x
3
) = Ψ
Ceq
(x
2
, x
3
) + k
2
x
2
, (9.235)
where k
2
> 0. It is straightforward to show that (9.234) and (9.235) satisfy
conditions (9.59)–(9.61) of Theorem 9.1.
Applying Theorem 9.1 to the system (9.231)–(9.233) yields the family
of control laws
u = φ(x
1
, x
2
, x
3
) = −R
−1
2
h
ˆ
P (x
1
− α(x
2
, x
3
)) +
1
2
L
2
(x
1
, x
2
, x
3
)
i
, (9.236)
with Lyapunov fun ction
V (x
1
, x
2
, x
3
) =
ˆ
P [x
1
−α(x
2
, x
3
)]
2
+
1
2
α
2
x
2
2
+
1
2
α
3
x
2
3
, (9.237)
where R
2
> 0 and
ˆ
P > 0. Fu rthermore, the performance functional
minimized by the control law (9.236) has the form
J(x
10
, x
20
, x
30
, ˆu) =
Z
∞
0
[L
1
(x
1
(t), x
2
(t), x
3
(t))
+L
2
(x
1
(t), x
2
(t), x
3
(t))ˆu(t) + R
2
ˆu
2
(t)]dt, (9.238)
where
L
1
(x
1
, x
2
, x
3
)
△
= R
2
φ
2
(x
1
, x
2
, x
3
) − V
′
sub
(x
2
, x
3
)[f(x
2
, x
3
) + G(x
2
, x
3
)x
1
]
+2[x
1
− α(x
2
, x
3
)]
ˆ
P α
′
(x
2
, x
3
)[f(x
2
, x
3
) + G(x
2
, x
3
)x
1
].
(9.239)
Now, L
2
(x
1
, x
2
, x
3
) must be chosen to satisfy condition (9.62) or, equiva-
lently,
(x
1
− α(x
2
, x
3
))
− 2x
1
− 2
ˆ
P
h
α
′
(x
2
, x
3
)(f(x
2
, x
3
) + G(x
2
, x
3
)x
1
)
+R
−1
2
[
ˆ
P (x
1
− α(x
2
, x
3
) +
1
2
L
T
2
(x
1
, x
2
, x
3
)]
i
< 0. (9.240)
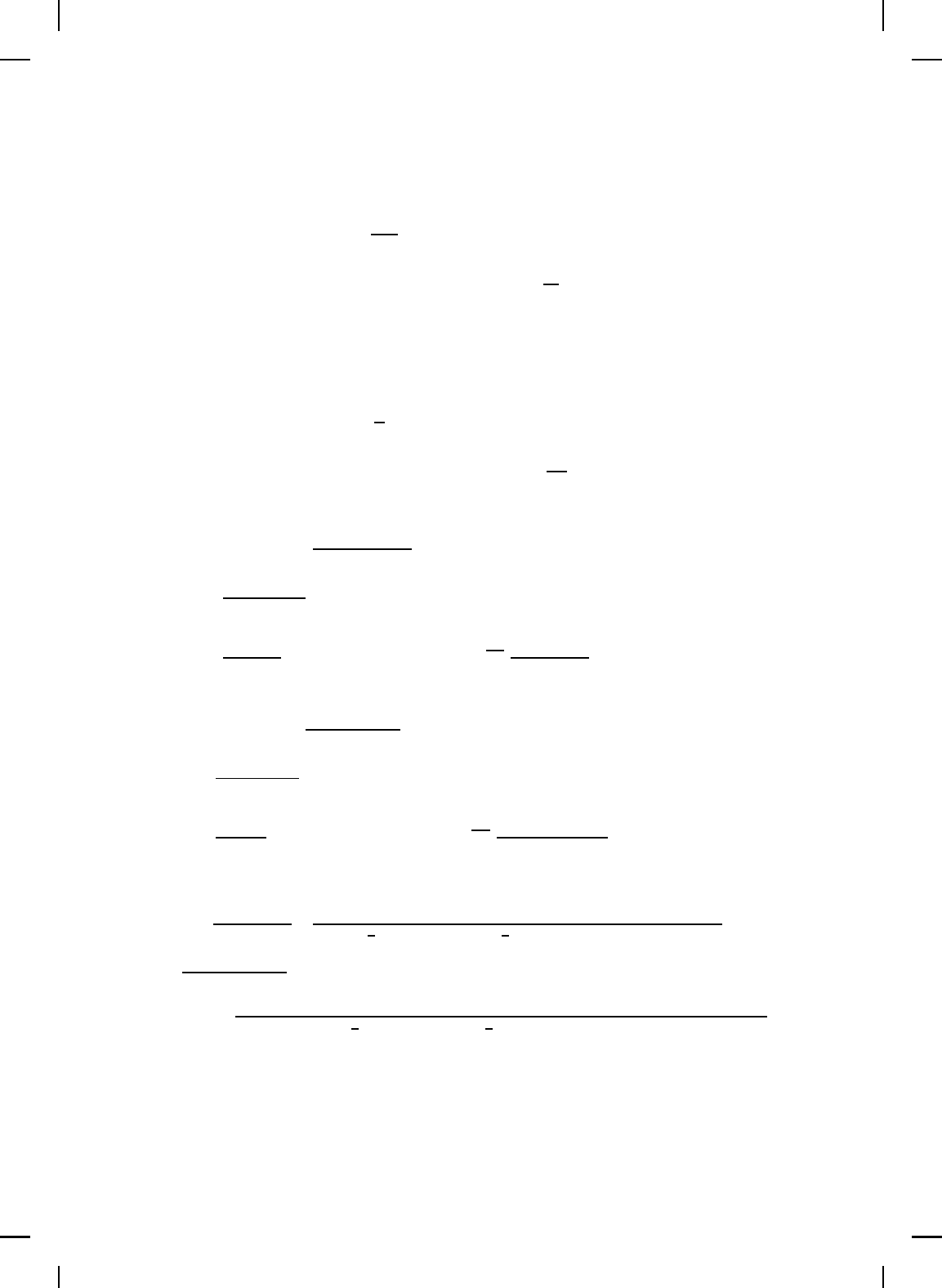
NonlinearBook10pt November 20, 2007
596 CHAPTER 9
A particular admissib le choice for L
2
(x
1
, x
2
, x
3
) satisfying (9.240) is
given by
L
2
(x
1
, x
2
, x
3
) = −
α
1
k
1
a
b(k
2
+ Ψ
c
eq
,x
2
(x
2
, x
3
))(Ψ
Ceq
(x
2
, x
3
) −x
1
)
−k
3
cΨ
c
eq
,x
3
(x
2
, x
3
)x
3
+
α
2
α
1
bx
2
, (9.241)
where α
1
△
= 2
ˆ
P and k
1
△
= R
−1
2
ˆ
P . For this choice of L
2
(x
1
, x
2
, x
3
) the feedback
control (9.236) becomes
φ(x
1
, x
2
, x
3
) = −k
1
(x
1
− Ψ
Ceq
(x
2
, x
3
) − k
2
x
2
)
+
1
a
b(k
2
+ Ψ
c
eq
,x
2
(x
2
, x
3
))(Ψ
Ceq
(x
2
, x
3
) −x
1
)
−k
3
cΨ
c
eq
,x
3
(x
2
, x
3
)x
3
+
α
2
α
1
bx
2
, (9.242)
where
Ψ
c
eq
,x
2
(x
2
, x
3
)
△
=
∂Ψ
Ceq
(x
2
, x
3
)
∂x
2
=
∂Ψ
c
(x
2
, x
3
)
∂x
2
(x
2
,x
3
)=(Φ
eq
+x
2
, Ω
eq
+x
3
)
=
γ
sh
σdx
2
3
γ
sh
− 1
[Ψ
c
(Φ
eq
+ x
2
, Ω
eq
+ x
3
) + 1]
1
γ
sh
∂η
c
(x
2
, x
3
)
∂x
2
(x
2
,x
3
)=(Φ
eq
+x
2
, Ω
eq
+x
3
)
,
Ψ
c
eq
,x
3
(x
2
, x
3
)
△
=
∂Ψ
c
eq
(x
2
, x
3
)
∂x
3
=
∂Ψ
c
(x
2
, x
3
)
∂x
3
(x
2
,x
3
)=(Φ
eq
+x
2
, Ω
eq
+x
3
)
=
γ
sh
σd
γ
sh
− 1
[Ψ
c
(Φ
eq
+ x
2
, Ω
eq
+ x
3
) + 1]
1
γ
sh
∂
x
2
3
η
c
(x
2
, x
3
)
∂x
3
(x
2
,x
3
)=(Φ
eq
+x
2
, Ω
eq
+x
3
)
,
and where
∂η
c
(x
2
, x
3
)
∂x
2
=
σx
2
3
(f
2
(x
3
f
1
− x
2
f
2
) + f
3
(σx
3
− x
2
f
3
) − 2x
2
(f
4
+ f
5
))
(σx
2
3
+
1
2
(x
3
f
1
− x
2
f
2
)
2
+
1
2
(σx
3
− x
2
f
3
)
2
+ x
2
2
(f
4
+ f
5
))
2
,
∂[x
2
3
η
c
(x
2
, x
3
)]
∂x
3
=
σx
3
3
(2σx
2
3
+(x
3
f
1
−2x
2
f
2
)(x
3
f
1
−x
2
f
2
)+(σx
3
−2x
2
f
3
)(σx
3
−x
2
f
3
)+4x
2
2
(f
4
+f
5
))
(σx
2
3
+
1
2
(x
3
f
1
− x
2
f
2
)
2
+
1
2
(σx
3
− x
2
f
3
)
2
+ x
2
2
(f
4
+ f
5
))
2
,
so that (9.241) satisfies
−α
1
k
1
a(x
1
− Ψ
Ceq
(x
2
, x
3
) −k
2
x
2
)
2
< 0, (x
1
, x
2
, x
3
) 6= (0, 0, 0). (9.243)

NonlinearBook10pt November 20, 2007
OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 597
In this case, the overall nonlinear controller
˜u
△
=
˜u
1
˜u
2
=
x
2
− ˆu
−k
3
x
3
+ f (x
2
, x
3
)
, (9.244)
guarantees that the closed-loop system (9.224)–(9.226) is globally asymp-
totically stable.
Next, with (a, b, c, d, e) = (9.37, 310.81, 6.97, 0.38, 0.7), (f
1
, f
2
, f
3
, f
4
,
f
5
) = (0.44, 1.07, 2.18, 0.17, 0.12), γ
sh
= 1.4, µ = 3, and σ = 0.9, we design
inverse optimal controllers for the three-state centrifugal compressor model
discussed above. Since the torque dynamics given by (9.219) is f or forward
mass flow in the compressor, and since the compressor may enter deep surge,
there is a n eed to derive an expression f or the compressor torque for negative
mass flow. Hence, assuming that a centrifugal compressor in reverse flow
can be viewed as a throttling device and, hence, can be approximated as a
turbine, it follows that [119]
˙
Ω(t) = c(u
2
(t) −σ|Φ(t)|Ω(t)), Ω(0) = Ω
0
, t ≥ 0. (9.245)
Using the initial conditions (Ψ
0
, Φ
0
, Ω
0
) = (0.188, 0.141, 0.394) and
the design parameters (α
1
, α
2
, α
3
) = (1, 0.1, 1) and (k
1
, k
2
, k
3
) = (1, 3, 1),
the closed-loop system response is compared to the open -loop response
when the compr ession system is taken from an operating speed of 20,000
rpm to 25,000 rpm. Figure 9.13 shows the p ressure-flow phase portrait of
the state trajectories when the system is taken from an operating speed
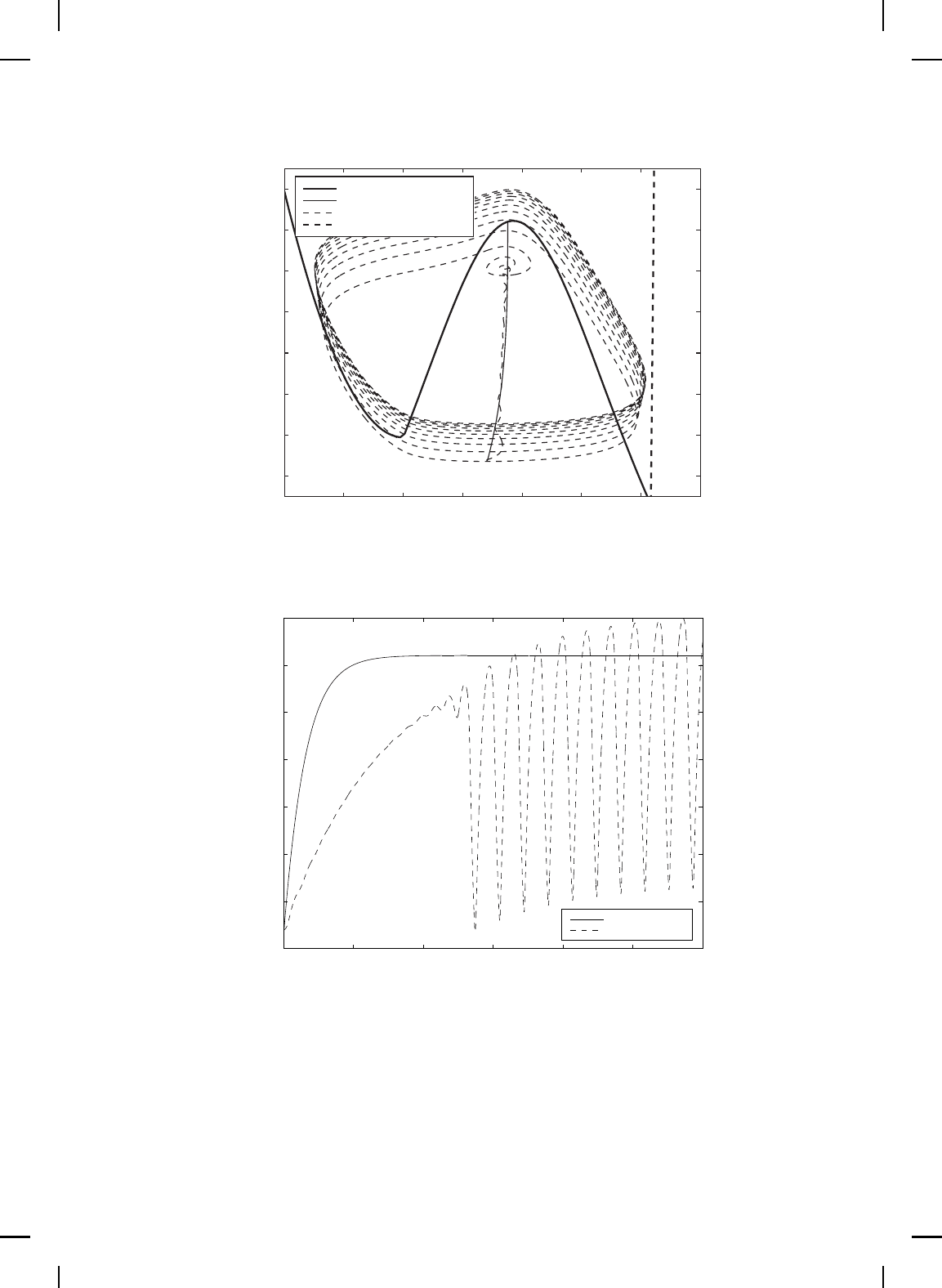
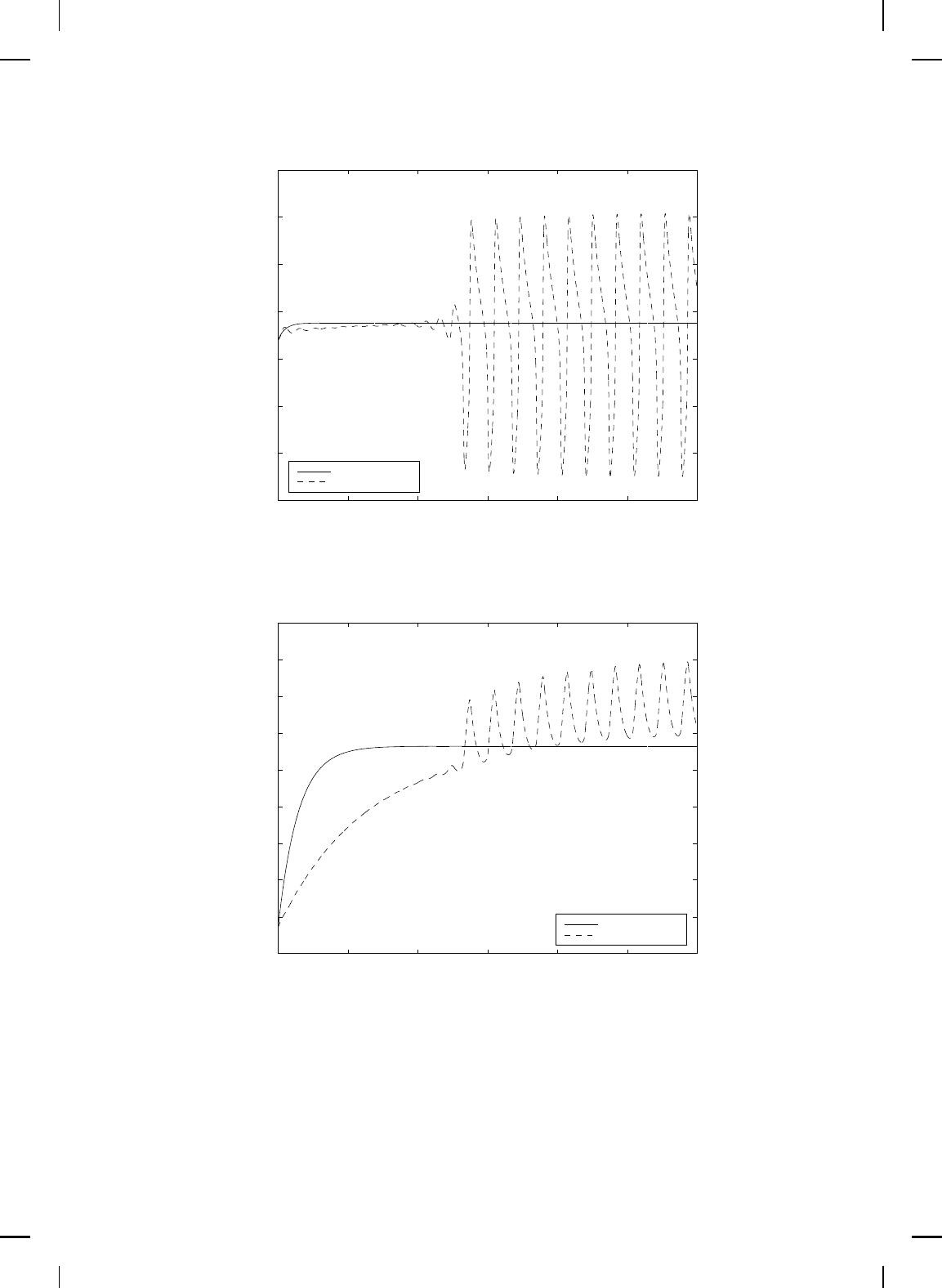
of 20,000 rpm to 25,000 rpm. The pressure rise, mass flow, an d spool
speed variations for the open-loop and controlled system are shown in
Figure 9.14, 9.15, and 9.16, respectively. Figures 9.17 and 9.18 shows
the control effort versus time. This comparison illustrates that open-loop
control drives the compression system into deep surge, while the proposed
globally stabilizing controller dr ives the system to the desired equilibrium
point (Ψ
eq
, Φ
eq
, Ω
eq
) = (0.304, 0.176, 0.493).
9.8 Problems
Problem 9.1. Consider the nonlinear dynamical system
˙x
1
(t) = 1 + x
2
(t) + [x
1
(t) − 1]
3
, x
1
(0) = x
10
, t ≥ 0, (9.246)
˙x
2
(t) = x
1
(t) + u(t), x
2
(0) = x
20
. (9.247)
Using backsteppin g, find a globally stabilizing feedback controller u(t) =
φ(x(t)) for (9.246) and (9.247).
Problem 9.2. Consider the nonlinear dynamical system
˙x
1
(t) = x
2
1
(t) − x
5
1
(t) + x
2
(t), x
1
(0) = x
10
, t ≥ 0, (9.248)
NonlinearBook10pt November 20, 2007
598 CHAPTER 9
-0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5
0.18
0.2
0.22
0.24
0.26
0.28
0.3
0.32
φ
ψ
Pressure-flow map
Closed-loop trajectory
Open-loop trajectory
Stone wall
Figure 9.13 Controlled and uncontrolled phase portrait of pressure-flow state trajectories
from 20,000 rpm to 25,000 rpm.
0 0.5 1 1.5 2 2.5 3
0.18
0.2
0.22
0.24
0.26
0.28
0.3
0.32
ξ
ψ
Closed-loop
Open-loop
Figure 9.14 Pressure rise versus time.
˙x
2
(t) = x
3
(t), x
2
(0) = x
20
, (9.249)
˙x
3
(t) = u(t), x
3
(0) = x
30
. (9.250)
NonlinearBook10pt November 20, 2007
OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 599
0 0.5 1 1.5 2 2.5 3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
ξ
φ
Closed-loop
Open-loop
Figure 9.15 Mass flow versus time.
0 0.5 1 1.5 2 2.5 3
0.38
0.4
0.42
0.44
0.46
0.48
0.5
0.52
0.54
0.56
ξ
ω
Closed-loop
Open-loop
Figure 9.16 Compressor spool speed versus time.
Using backsteppin g, find a globally stabilizing feedback controller u(t) =
φ(x(t)) for (9.248)–(9.250).

NonlinearBook10pt November 20, 2007
600 CHAPTER 9
0 0.5 1 1.5 2 2.5 3
0.07
0.08
0.09
0.1
0.11
0.12
0.13
0.14
0.15
0.16
ξ
τ
Figure 9.17 Driving torque versus time.
Problem 9.3. Consider the nonlinear dynamical system
˙x
1
(t) = x
2
(t) −x
3
1
(t), x
1
(0) = x
10
, t ≥ 0, (9.251)
˙x
2
(t) = u(t), x
2
(0) = x
20
. (9.252)
Using backstepping, find a stabilizing controller u(t) = φ(x(t)) for (9.251)
and (9.252).
Problem 9.4. Consider the nonlinear dynamical system
˙x
1
(t) = cos x
1
(t) −x
3
1
(t) + x
2
(t), x
1
(0) = x
10
, t ≥ 0, (9.253)
˙x
2
(t) = u(t), x
2
(0) = x
20
. (9.254)
Using backstepping, fi nd a globally stabilizing controller u(t) = φ(x(t)) for
(9.253) and (9.254).
Problem 9.5. Consider the nonlinear dynamical system
˙x
1
(t) = −x
1
(t) + x
2
(t)x
2
1
(t), x
1
(0) = x
10
, t ≥ 0, (9.255)
˙x
2
(t) = u(t), x
2
(0) = x
20
. (9.256)
Using backstepping, fi nd a globally stabilizing controller u(t) = φ(x(t)) for
(9.255) and (9.256).
Problem 9.6. Consider the nonlinear dynamical system
˙x
1
(t) = −x
3
1
(t) −[αx
2
(t) + βx
3
(t)]x
3
1
(t), x
1
(0) = x
10
, t ≥ 0, (9.257)

NonlinearBook10pt November 20, 2007
OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 601
0 0.5 1 1.5 2 2.5 3
0.1
0.15
0.2
0.25
0.3
0.35
0.4
γ
th
ξ
Figure 9.18 Throttle opening versus time.
˙x
2
(t) = x
3
(t), x
2
(0) = x
20
, (9.258)
˙x
3
(t) = u(t), x
3
(0) = x
30
, (9.259)
where αβ ≥ 0. Using backstepping, find a stabilizing controller u(t) =
φ(x(t)) for (9.257)–(9.259). Can the sys tem be globally stabilized if αβ < 0?
Problem 9.7. Consider the nonlinear cascade system (9.160)–(9.162).
Show that if (9.171) and (9.172) are satisfied then the following statements
hold:
i) V
c
(y, z) given by (9.165) exists and is continuous in R
m
× R
q−m
.
ii) V (x, y, z) given by (9.175) is positive defi nite in R
n
× R
m
× R
q−m
.
iii) V (x, y, z) given by (9.175) is radially unbounded.
Problem 9.8. Show that if V : R
q−m
→ R is a radially unbounded,
nonnegative-definite polynomial function, then condition (9.172) is s atisfied.
Problem 9.9. Consider the three-state parameterized Moore-Greitzer
model given by (9.195)–(9.197). Show that the linearized system is
linearly stabilizable for λ > 1, while for λ = 1, corresponding to the
maximum pressure rise equilibrium point, the linearized system is not
linearly stabilizable.

NonlinearBook10pt November 20, 2007
602 CHAPTER 9
Problem 9.10. Show that if Ψ
C
(·) in (9.183) and (9.184) is analytic,
then the integral terms in (9.183) and (9.184) can be expressed in terms of
an infinite Taylor expans ion about the circumferentially average flow Φ(·)
to give (9.186) and (9.187).
Problem 9.11. To address only surge instabilities in axial flow
compressor systems we restrict the three-state Moore-Greitzer model given
by (9.199)–(9.201) to the invariant m anifold wh ere the rotating stall
amplitude is zero, to obtain a two-state surge model. In this case,
˙
Φ
s
(t) = −
3
2
Φ
2
s
(t) −
1
2
Φ
3
s
(t) −Ψ
s
(t), Φ
s
(0) = Φ
s0
, t ≥ 0, (9.260)
˙
Ψ
s
(t) = −u(t), Ψ
s
(0) = Ψ
s0
, (9.261)
where Φ
s
is the shifted axial average mass flow in the comp ressor, Ψ
s
is the shifted total-to-static pressure rise, and u is the control input.
Using T heorem 9.1, design a globally stabilizing controller for this system.
Compare the state response and control effort to the feedback linearizing
controller given by
u = φ
FL
(Φ
s
, Ψ
s
) = −100Φ
s
+(5−3Φ
s
−1.5Φ
2
s
)(Ψ
s
+1.5Φ
2
s
+0.15Φ
3
s
). (9.262)
9.9 Notes and References
Integrator backstepping for cascade and block cascade systems can be traced
back to the works of Tsinias [433], Koditschek [240], Byrnes and Isidori [75],
and Sontag and Sus smann [408]. Block cascade integrator backstepping
via passivity notions was developed by Kokotovi´c and Su s smann [241]
and extended to nonlinear block cascade sys tems by Or tega [339] and
Byrnes, Isidori, and Willems [77]. Further extensions were reported in
Lozano, Brogliato, and Landau [287]. Recursive backstepping designs were
reported in Saberi, Kokotovi´c, and Sussmann [376] and Kanellakopou los,
Kokotovi´c, and Morse [231]. For a textbook treatment of recursive integrator
backstepping design see Krsti´c, Kanellakopoulos, and Kokotovi´c [247].
The optimality and inverse optimality framework of integrator back-
stepping presented in Sections 9.3–9.5 were adopted from Haddad, Fausz,
Chellaboina, and Abdallah [169]. Optimality issues for backstepping-like
designs are also presented in Kolesnikov [242]. The Lyapunov function
involving cross-terms in Section 9.5 and Problem 9.7 was introduced by
Sepulchre, Jankovi´c, and Kokotovi´c [395].

NonlinearBook10pt November 20, 2007
Chapter Ten
Disturbance Rejection Control for
Nonlinear Dynamical Systems
10.1 Introduction
One of the fundamental problems in the analysis and feedback control design
of linear systems is the ability of the control system to reject uncertain
exogenous disturbances. To this end, H
∞
control theory has been developed
to address the problem of disturbance rejection for linear systems with
bounded energy (square-integrable) L
2
signal norms on the disturbances
and performance variables [121, 122, 478]. Since in this case the induced
H
∞
transfer function norm corresponds to the worst-case d isturbance
attenuation, for systems w ith poorly modeled disturbances which possess
significant power within arbitrarily small bandwidths H
∞
theory is clearly
appropriate. For linear finite-dimensional, time-invariant systems the H
∞
control design problem has been thoroughly investigated in recent years (see,
for example, [111, 237, 353, 355] and the numerous references therein). In
particular, the H
∞
control design problem was formulated in the state space
setting and was s hown to correspond to a two-person zero-sum differential
game problem, wherein the existence of an H
∞
(sub)optimal controller is
equivalent to the existence of a s olution to an algebraic Riccati equation
arising in quadratic differential game theory [31, 32,296].
Alternatively, the H
∞
analysis and synthesis control problem can
also be formulated and solved in the state space setting using the notion
of dissipativity theory [11]. In particular, us ing the bounded real Riccati
equation it follows that the H
∞
norm of a (closed-loop) linear system is less
than a prespecified positive number γ if and only if the (closed-loop) linear
system is nonexpansive with respect to an appropriate qu ad r atic supply rate
involving the systems weighted input energy and output energy. Riccati-
equation-based results f or the mixed-norm H
2
/H
∞
problem [49, 112, 238]
have also been developed using dissipativity notions to allow the trade-
off between systems with stochastic white noise disturbance models (H
2
)
possessing a fixed covariance (power spectral density) and deterministic

NonlinearBook10pt November 20, 2007
604 CHAPTER 10
bounded energy disturbance mod els. As in the pure H
∞
case, the mixed-
norm H
2
/H
∞
problem can be compared to a game-theoretic framework
involving a Nash differential game problem [279].
Using a n onlinear game-theoretic framework the authors in [22, 31]
replace the algebraic Riccati equation arising in linear H
∞
theory with
a particular Hamilton-Jacobi-Bellman equation (the Isaacs equation) to
obtain a nonlinear equivalent to the H
∞
analysis and synthesis control
problem. Sufficient conditions for the existence of stabilizing solutions of the
Isaacs equation are given in [438–440] in terms of the existence of a linear
(sub)optimal H
∞
controller for the linearized (about a given equilibriu m
point) nonlinear controlled system. In parallel research, the authors in
[213–216] use nonlinear dissipativity theory [77,188,189,191,320,456,457] for
nonlinear affine systems with appropriate storage functions and quadratic
supply rates to obtain nonexpansive (gain bounded) closed-loop s ystems.
Although a nonlinear equivalent to H
∞
analysis and synthesis has been
developed it is important to note that the methods and results discussed
in [22,31,213–216,438–440] are independent of optimality considerations. In
this chapter, we develop an optimality-based theory for disturbance rejection
for nonlinear systems with bounded exogenous d isturbances. T he key
motivation for developing an optimal and inverse optimal nonlinear control
theory that additionally gu arantees disturbance rejection is th at it provides
a class of candidate disturbance rejection controllers parameterized by the
cost functional that is minimized. In the case of linear systems, optimality-
based theories have proven extremely successful in numerous applications.
Specifically, to fully address the trade-offs between H
2
and H
∞
performance,
the optimality-based linear-quadratic control problem was merged with H
∞
methods to address the m ixed-norm H
2
/H
∞
control problem [49, 238].
In order to address the op timality-based disturbance rejection non-
linear control problem we extend the nonlinear-nonquadratic, continuous-
time controller analysis and synthesis framework presented in Chapter 8.
Specifically, using nonlinear dissipativity th eory with appropriate storage
functions and supply rates we transform the nonlinear disturbance rejection
problem into an optimal control pr ob lem. This is accomplished by pr operly
modifying the cost functional to account for exogenous disturbances so that
the solution of the modified optimal nonlinear control problem serves as th e
solution to the distu rbance rejection problem.
The framework guarantees that the closed-loop nonlinear input-output
map is dissipative with respect to general supply rates. Specializing to
quadratic sup ply rates involving net system energy flow and weighted input
and output energy, the results guarantee passive and nonexpansive (gain
