Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 575

applied to the system

˜x(t) =

f(˜x(t)) +

G(˜x(t))u(t), ˜x(0) = ˜x

, t ≥ 0, (9.133)

where

˜x =



ˆx



f(˜x) =



f(x) + G(x)y

f(ˆx)



G(˜x) =



G(ˆx)



Speciﬁcally, conditions (8.59)–(8.62) are trivially satisﬁed by (9.126), (9.127),

and (9.130). Next, using (9.128) and (9.133), φ(x, ˆx) can be written as

φ(˜x) = −

−1

(˜x)(L

(˜x) +

(˜x)V

′T

(˜x)) (9.134)

so that (8.65) is satisﬁed. Finally, using (9.130) and (9.133) it follows that

(9.131) or, equivalently,

(˜x) = φ

(˜x)R

(˜x)φ(˜x) − V

′

(˜x)

f(˜x) (9.135)

satisﬁes (8.66).

A particular choice of L

(x, ˆx) satisfying condition (9.127) is given by

(x, ˆx) =



′

sub

(x)G(x) − 2k

(ˆx)



(x, ˆx). (9.136)

In this case, the feedback control φ(x, ˆx) is given by

φ(x, ˆx) = k(ˆx) −



−1

(x, ˆx)

(ˆx)V

′T

(ˆx) + G

(x)V

′T

sub

(x)



. (9.137)

Alternatively, choosing L

(x, ˆx) satisfying condition (9.127) by

(x, ˆx) = V

′

sub

(x)G(x)R

(x, ˆx) −2k

(ˆx)R

(x, ˆx) + V

′

(ˆx)

G(ˆx), (9.138)

the f eedback control φ(x, ˆx) given by (9.128) specializes to

φ(x, ˆx) = k(ˆx) −

(x)V

′T

sub

(x). (9.139)

In the case where m = 1, (9.139) specializes to the control law obtained in

Lemma 2.17 of [247].

Next, we consider a class of systems given by (9.121)–(9.123) in which

the subsystem (9.121) is assumed to be globally stabilizable at x = 0 through

y in stead of having a globally asymptotically stable equilibrium at x = 0

with y = 0. Furthermore, we assume that the zero dynamics of a nonlinear

system are asymptotically stable with respect to the signals by which they

are driven. Thus , the following result is a nonlinear analog to Theorem 9.4.

Here, we assume that the vector ﬁeld

G(L

−1

is complete and involutive.

Theorem 9.6. Consider the nonlinear cascade system (9.121)–(9.123)

with performance functional (9.100) where L(x, ˆx, u) is given by

L(x, ˆx, u) = L

(x, ˆx) + L

(x, ˆx)(h

′

(ˆx)

f(ˆx) + h

′

(ˆx)

G(ˆx)u) + (h

′

(ˆx)

f(ˆx)

NonlinearBook10pt November 20, 2007

576 CHAPTER 9

′

(ˆx)

G(ˆx)u)

(x, ˆx)(h

′

(ˆx)

f(ˆx) + h

′

(ˆx)

G(ˆx)u), (9.140)

where u ∈ R

, L

: R

×R

→ R, L

: R

×R

→ R

1×m

satisﬁes L

(0, 0) = 0,

and R

: R

×R

→ P

. Assume that there exist continuously diﬀerentiable

functions α : R

→ R

and V

sub

: R

→ R such that

α(0) = 0, (9.141)

sub

(0) = 0, (9.142)

sub

(x) > 0, x ∈ R

, x 6= 0, (9.143)

′

sub

(x)[f(x) + G(x)α(x)] < 0, x ∈ R

, x 6= 0. (9.144)

Furth ermore, let L

(x, ˆx) satisfy

(y − α(x))



(x)V

′T

sub

(x) − 2

′

(x)(f(x) + G(x)y)

−1

(x, ˆx)[

P (y − α(x)) +

(x, ˆx)]



< 0, (x, y) ∈ R

× R

, y 6= α(x),

(9.145)

where

P ∈ R

m×m

is an arbitrary positive-deﬁnite matrix, and assume that

(9.122) and (9.123) has constant relative degree {1, 1, . . . , 1} globally deﬁned

uniformly in x with input-to-state stable zero dynamics. Then the zero

solution (x(t), ˆx(t)) ≡ (0, 0) of the cascade system (9.121)–(9.123) is globally

asymptotically stable with the feedback control law

u = (h

′

(ˆx)

G(ˆx))

−1

[v − h

′

(ˆx)

f(ˆx)], (9.146)

where

v = φ(x, ˆx) = −R

−1

(x, ˆx)

P (y − α(x)) −

−1

(x, ˆx)L

(x, ˆx). (9.147)

Furth ermore,

J(x

, ˆx

, (h

′

(ˆx)

G(ˆx))

−1

(φ(x, ˆx) −h

′

(ˆx)

f(ˆx))) = V (x

, h(ˆx

)),

, ˆx

) ∈ R

× R

, (9.148)

where

V (x, y) = V

sub

(x) + [y − α(x)]

P [y − α(x)], (9.149)

and the performan ce functional (9.140), with

(x, ˆx) = φ

(x, ˆx)R

(x, ˆx)φ(x, ˆx) − V

′

sub

(x)(f(x) + G(x)y)

+2(y − α(x))

P α

′

(x)(f(x) + G(x)y), (9.150)

is minimized in the sense that

J(x

, ˆx

, (h

′

(ˆx)

G(ˆx))

−1

(φ(x, ˆx) −h

′

(ˆx)

f(ˆx)))

= min

u(·)∈S(x

,ˆx

)

J(x

, ˆx

, u(·)), (x

, ˆx

) ∈ R

× R

(9.151)

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 577

Proof. Since the nonlinear subsystem (9.122) and (9.123) has relative

degree {1, 1, . . . , 1}, it follows from Lemma 6.2 that there exists a global

diﬀeomorphism T : R

→ R

such that, in the coordinates





△

= T (ˆx), (9.152)

the nonlinear diﬀerential equation (9.122) is equivalent to the normal form

˙y(t) = h

′

(ˆx(t))[

f(ˆx(t)) +

G(ˆx(t))u(t)], y(0) = h(ˆx

), t ≥ 0, (9.153)

˙z(t) = f

(z(t)) + r(z(t), y(t))y(t), z(0) = z

, (9.154)

where f

: R

(q−m)

→ R

(q−m)

and r : R

(q−m)

× R

→ R

(q−m)×m

. Next,

applying the linearizing feedback transformation (9.146) to (9.153) yields

the trans formed cascade system

˙x(t) = f(x(t)) + G(x(t))y(t), x(0) = x

, t ≥ 0, (9.155)

˙y(t) = v(t), y(0) = h(ˆx

), (9.156)

˙z(t) = f

(z(t)) + r(z(t), y(t))y(t), z(0) = z

. (9.157)

Initially ignoring the zero dynamics (9.157), it follows from Theorem

9.1, with ˆx replaced by y and u replaced by v, that the equilibrium x = 0,

y = 0 with the feedback control law v = φ(x, y), where φ(x, y) is given by

(9.147), is asymptotically stable. Now, since the zero dynamics subsystem

(9.157) is input-to-state stable and the zero solution y(t) ≡ 0 to (9.156)

can be made asymptotically stable, y(t) is bounded and lim

t→∞

y(t) = 0.

Hence, it f ollows from Proposition 4.2 that the zero solution z(t) ≡ 0 to

(9.157) is globally asymptotically stable. Furthermore, since ˆx = T

−1

(y, z),

global asymptotic stability of the zero s olution (y(t), z(t)) ≡ (0, 0) to (9.156)

and (9.157) implies global asymptotic stability of the zero solution ˆx(t) ≡ 0

to (9.122).

Next, with (9.155), (9.156), (9.140), and (9.149), the Hamiltonian has

the f orm

H(x, ˆx, u) = L

(x, ˆx) + L

(x, ˆx)(h

′

(ˆx)

f(ˆx) + h

′

(ˆx)

G(ˆx)u) + (h

′

(ˆx)

f(ˆx)

′

(ˆx)

G(ˆx)u)

(x, ˆx)(h

′

(ˆx)

f(ˆx) + h

′

(ˆx)

G(ˆx)u)

′

sub

(x)(f(x) + G(x)y) + 2(y − α(x))

P [h

′

(ˆx)

f(ˆx)

′

(ˆx)

G(ˆx)u − α

′

(x)(f(x) + G(x)y)]. (9.158)

Now, the feedback control law (9.146) is obtained by setting

∂H

∂u

= 0. Using

(0, 0) = 0 it follows that φ(0, 0) = 0, which pr oves (8.43). Next, with

(x, ˆx) given by (9.150) it follows that (8.46) holds. Finally, since

H(x, ˆx, u) = [v − φ(x, ˆx)]

(x, ˆx)[v − φ(x, ˆx)],

NonlinearBook10pt November 20, 2007

578 CHAPTER 9

and R

(x, ˆx) > 0, (x, ˆx) ∈ R

× R

, (8.45) holds. The result now follows as

a direct consequence of Th eorem 8.2.

A particular choice of L

(x, ˆx) satisfying condition (9.145) is given by

(x, ˆx) =

−1

(x)V

′T

sub

(x) − 2α

′

(x)(f(x) + G(x)y)

(x, ˆx). (9.159)

In this case, for u(t) ∈ R, t ≥ 0, the control law given by (9.146) s pecializes

to the n onlinear backstepping controller obtained in Lemma 2.25 of [247] by

setting

P =

and R

(x, ˆx) = 1/c.

Finally, we consider nonlinear cascade systems of the form

˙x(t) = f (x(t)) + G(x(t))y(t), x(0) = x

, t ≥ 0, (9.160)

˙y(t) = h

′

(ˆx(t))

f(ˆx(t)) + h

′

(ˆx(t))

G(ˆx(t))u(t), ˆx(0) = ˆx

, (9.161)

˙z(t) = f

(z(t)) + r(y(t), z(t))y(t), z(0) = z

, (9.162)

where the zero solution z(t) ≡ 0 to (9.162) is asymptotically stable,

, z

]

△

= T (ˆx), and T (·) is given by (9.152). Th e system (9.160)–(9.162)

can be viewed as the normal form equivalent of (9.121)–(9.123), where the

input subsystem (9.122) and (9.123) is minimum phase with relative degree

{1, 1, . . . , 1}, obtained by applying the global diﬀeomorphism (9.152). In

this case, the stability assumption on (9.162) is implied by the minimum

phase assu mption on (9.122) and (9.123). For the cascade nonlinear system

(9.160)–(9.162), we consider the perf ormance functional

J(x

, h(ˆx

), z

, u) =

∞

L(x(t), y(t), z(t), u(t))dt, (9.163)

where

L(x, y, z, u) = L

(x, y, z) + L

(x, y, z)u + u

(x, y, z)u. (9.164)

Furth ermore, deﬁne

(y, z)

△

∞

′

(¯z(s))r(¯y(s), ¯z(s))¯y(s)ds, (9.165)

where ¯y(τ ) and ¯z(τ), τ ≥ 0, are solutions of (9.160) an d (9.161), respectively,

with initial conditions ¯y(0) = y and ¯z(0) = z, and V

(z) is a Lyapu nov

function f or the asymptotically stable (by assumption) subsystem (9.162).

Note that the time derivative of V

(y, z) along the trajectories of y and z is

given by

(y, z) = −V

′

(z)r(y, z)y.

Theorem 9.7. Consider the nonlinear cascade system (9.160)–(9.162)

with performance functional (9.163), where L(x, y, z, u) is given by (9.164)

and where u ∈ R

, L

(x, y, z) : R

×R

q−m

→ R, L

(x, y, z) : R

×R

q−m

→ R

1×m

satisﬁes L

(0, 0, 0) = 0, and R

: R

× R

q−m

→ P

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 579

Assume that there exist continuously diﬀerentiable functions α : R

→ R

and V

sub

: R

→ R such that

α(0) = 0, (9.166)

sub

(0) = 0, (9.167)

sub

(x) > 0, x ∈ R

, x 6= 0, (9.168)

′

sub

(x)[f(x) + G(x)α(x)] < 0, x ∈ R

, x 6= 0. (9.169)

Furth ermore, let L

(x, y, z) satisfy

(y − α(x))



(x)V

′T

sub

(x) + 2

′

(ˆx)

f(ˆx) − α

′

(x)(f(x) + G(x)y)

−h

′

(ˆx)

G(ˆx)R

−1

(x, y, z)((h

′

(ˆx)

G(ˆx))

P (y − α(x)) +

(x, y, z))



< 0,

(x, y, z) ∈ R

× R

q−m

, y 6= α(x), (9.170)

where

P ∈ R

m×m

is an arbitrary positive-deﬁnite matrix, assume that the

zero solution z(t) ≡ 0 to (9.162) with y = 0 is globally asymptotically stable

with Lyapunov function V

(z), assume there exist continuously d iﬀerentiable

functions γ

, γ

∈ K

∞

such that

kr(y, z)k ≤ γ

(kyk) + γ

(kyk)kzk, (9.171)

and assume there exist k, c > 0 such that kzk > c implies



∂V

(z)

∂z



kzk ≤ kV

(z). (9.172)

Then the zero s olution (x(t), y(t), z(t)) ≡ (0, 0, 0) of the cascade system

(9.160)–(9.162) is globally asymp totically stable w ith the feedback control

law u = φ(x, y, z), where

φ(x, y, z) = −R

−1

(x, y, z)(h

′

(ˆx)

G(ˆx))

P (y − α(x))

−

−1

(x, y, z)L

(x, y, z). (9.173)

Furth ermore,

J(x

, h(ˆx

), z

, φ(·, ·, ·)) = V (x

, h(ˆx

), z

), (x

, ˆx

, z

) ∈ R

× R

q−m

(9.174)

where

V (x, y, z) = V

sub

(x) + (y − α(x))

P (y − α(x)) + V

(y, z) + V

(z), (9.175)

and the performan ce functional (9.163), with

(x, y, z) = φ

(x, y, z)R

(x, y, z)φ(x, y, z) − V

′

sub

(x)(f(x) + G(x)y)

−V

′

(z)f

(z) + (y − α

′

(x))

[α

′

(x)(f(x) + G(x)y) − h

′

(ˆx)

f(ˆx)],

(9.176)

NonlinearBook10pt November 20, 2007

580 CHAPTER 9

is minimized in the sense that

J(x

, h(ˆx

), z

, φ(x, y, z)) = min

u(·)∈S(x

,ˆx

)

J(x

, h(ˆx

), z

, u(·)),

, ˆx

, z

) ∈ R

× R

q−m

. (9.177)

Proof. Since the subsystem (9.162) has an asymp totically stable

equilibrium at z(t) = 0, t ≥ 0, it follows from Theorem 3.9 that there

exists a continuously diﬀerentiable positive-deﬁnite function V

(z) such that

′

(z)f

(z) < 0, z ∈ R

q−m

, z 6= 0. (9.178)

Next, since r(y, z) and V

(z) satisfy (9.171) and (9.172), V

sub

(x) satisﬁes

(9.167) and (9.168), and, with

P > 0, it follows that the Lyapunov function

candidate (9.175) is positive deﬁnite (see Problem 9.7). The resu lt now

follows as a direct consequence of Theorem 8.3 applied to the system

˜x(t) =

f(˜x(t)) +

G(˜x(t))u(t), ˜x(0) = ˜x

, t ≥ 0, (9.179)

where

˜x =









f(˜x) =





f(x) + G(x)y

′

(ˆx)

f(ˆx)

(z) + r(y, z)y





G(˜x) =





′

(ˆx)

G(ˆx)





Speciﬁcally, conditions (8.59)–(8.62) are satisﬁed by L

(0, 0, 0) = 0, (9.166)–

(9.170) and (9.175). Next, using (9.173) and (9.179), φ(x, y, z) can be

written as

φ(˜x) = −

−1

(˜x)[L

(˜x) +

(˜x)V

′T

(˜x)] (9.180)

so that (8.65) is satisﬁed. Finally, using (9.175) and (9.179) it follows that

(9.176) or, equivalently,

(˜x) = φ

(˜x)R

(˜x)φ(˜x) − V

′

(˜x)

f(˜x) (9.181)

satisﬁes (8.66).

Assumption (9.171) requires that r(y, z) of (9.162) has, at m ost, a

linear growth in z. While this unavoidably narrows the class of admissible

nonlinear systems which can be considered, it is n ot restrictive when the

input subsystem (9.161) and (9.162) is linear so that the zero dynamics

subsystem has the form (9.115). In this case, r(y, z) = B

, where B

is a constant matrix, and hence, (9.171) is automatically satisﬁed. More

generally, assumption (9.172) is satisﬁed by Lyapunov functions involving

positive deﬁnite, radially unbou nded polynomial functions of z (see Problem

9.8). Finally, a choice of L

(x, y, z) satisfying condition (9.170) is given by

(x, y, z) = 2[h

′

(ˆx)

f(ˆx) +

−1

(x)V

′T

sub

(x)

−α

′

(x)(f(x) + G(x)y)]

′

(ˆx)

G(ˆx))

−T

(x, y, z). (9.182)

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 581

9.6 Rotating Stall and Surge Control for Axial

Compression Systems

The desire to develop an integrated control s ys tem design methodology

for ad vanced propulsion sy s tems has led to signiﬁcant activity in mod-

eling and control of ﬂow compression systems in recent years (see, for

example, [2, 19, 35, 103, 140,141, 143, 248, 249, 277, 318, 319, 345, 451] and the

numerous r eferences th erein). Two predominant aerodynamic instabilities

in compression systems are rotating stall and sur ge. Rotating stall

is an inherently three-dimensional

local comp ression system oscillation

which is characterized by regions of ﬂow that rotate at a fraction of the

compressor rotor speed while su rge is a one-dimensional axisymmetric global

compression system oscillation, which involves axial ﬂow oscillations and in

some cases even axial ﬂow reversal, which can damage engine components

and cause ﬂameout to occur.

Rotating stall and surge arise due to perturbations in stable system

operating conditions involving steady, axisymmetric ﬂow and can severely

limit compressor performance. The transition f rom stable compressor

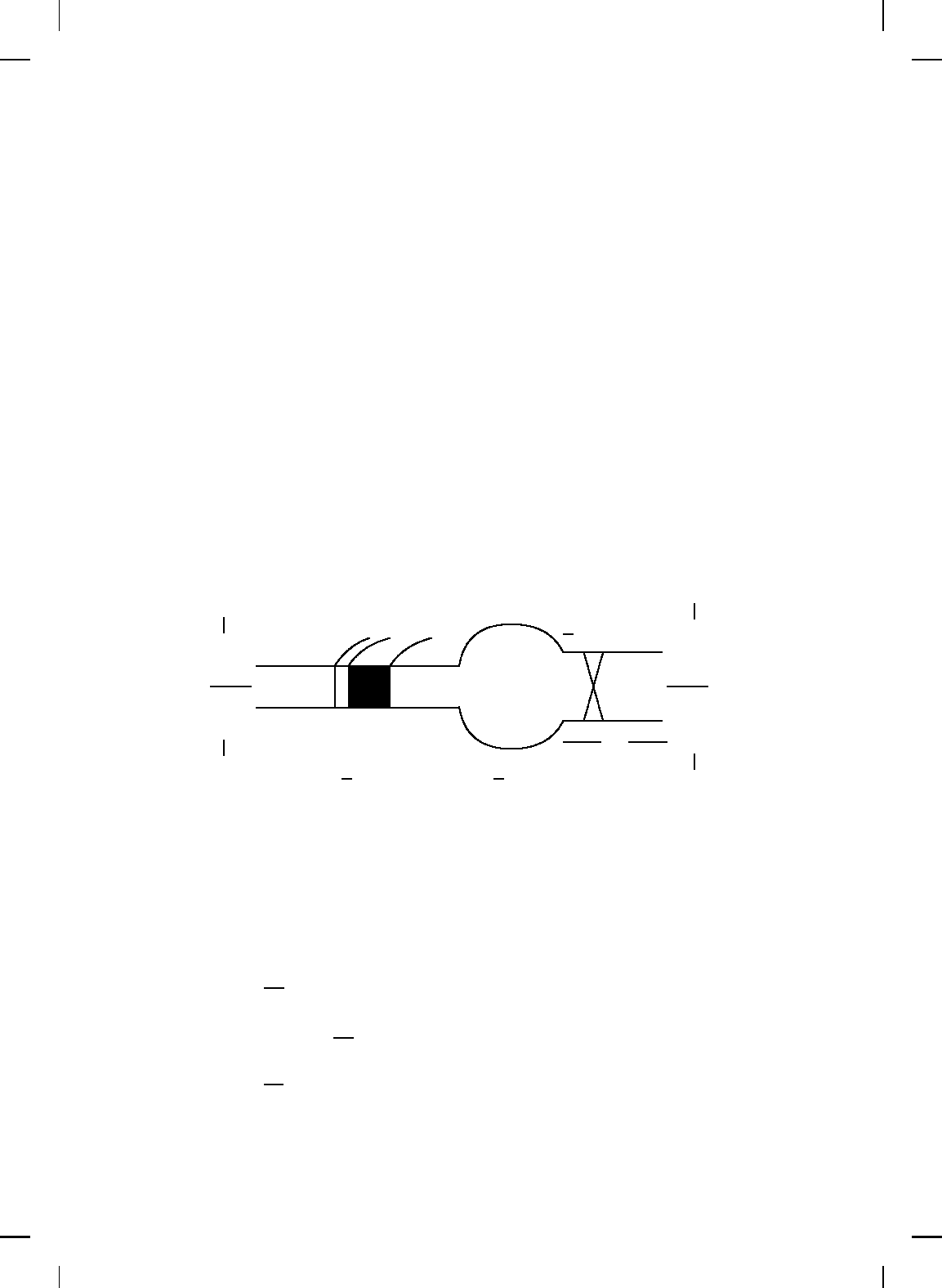
operating conditions to rotating stall and s urge is shown in Figure 9.2

representing a schematic of a compressor characteristic map where the

Flow

Pressure

Closing throttle

Rotating

Stall

Surge

Figure 9.2 Schematic of compressor characteristic map for a typical compression system

(−−−−stable equilibria, −−− unstable equilibria).

When analyzing high hub-to-tip ratio compressors , rotating stall can b e approximated as a

two-dimensional compression system oscillation.

NonlinearBook10pt November 20, 2007

582 CHAPTER 9

abscissa corresponds to the circumferentially averaged mass ﬂow through

the compressor and the ordinate corresponds to the normalized total-

to-static pressure rise in the compressor. For maximum compressor

performance, operating conditions require that the pressure rise in the

compressor correspond to the maximum pressure operating point on the

stable axisymmetric branch for a given throttle opening. Here, we

distinguish between compressor performance (pr essure rise) and compressor

eﬃciency (speciﬁc power consumption) where, depending on how the

compressor is designed, the most eﬃcient operating point may be to the

right of the peak of the compressor characteristic map. In practice, however,

compression system uncertainties and compression system d isturbances can

perturb the operating point into an unstable r egion d riving the system to

a stalled stable equilibrium, a stable limit cycle (surge), or both. In the

case of rotating stall, an attempt to recover to a high pressure operating

point by increasing the ﬂow through the throttle traps the s ystem within a

ﬂow range corresponding to two stable operating conditions involving steady

axisymmetric ﬂow and rotating stall resulting in severe hysteresis.

To avoid rotating stall and surge, trad itionally system designers allow

for a safety margin (rotating stall or surge margin) in compression system

operation. However, to account for compression system uncertainties such

as system modeling errors, in-service changes due to aging, etc., and

compression system disturbances such as compressor speed ﬂuctuations,

combustion noise, etc., operating at or below the rotating stall/surge margin

signiﬁcantly reduces the eﬃciency of the compression system. In contrast,

active control can enhance stable compression system operation to achieve

peak compressor performance. However, compression system uncertainty

and compression system disturbances are often signiﬁcant and the need for

robust disturbance rejection control is severe.

In order to develop control system design methodologies for compres-

sion systems, reliable models capturing th e intricate physical phenomena

of rotating stall and surge are necessary. A fundamental development in

compression system modeling for low speed axial compressors is the Moore-

Greitzer m odel given in [319]. Speciﬁcally, utilizing a one-mode expansion of

the disturbance velocity potential in the compression system and assuming

a nonlinear (cubic) characteristic for the compr essor performance map, the

authors in [319] develop a low-order, three-state nonlinear model involving

the mean ﬂow in the compressor, the pressure rise, and the amp litude

of rotating stall. Starting from inﬁ nitesimal perturbations in the ﬂow

ﬁeld the model captures the development of rotating stall and surge.

In particular, the model pr ed icts the experimentally veriﬁed subcritical

pitchfork bifurcation at the onset of rotating stall [311]. Extensions to the

Moore-Greitzer model that include blade row time lags and viscous transport

NonlinearBook10pt November 20, 2007

OPTIMAL INTEGRATOR BACKSTEPPING CONTROL 583

terms have been reported in [187] and [1,2, 451], respectively.

In this section, we apply the inverse optimal backstepping control

framework to the control of rotating stall and surge in j et engine compression

systems. To capture poststall transients in axial ﬂow compression systems

we use the one-mode Galerkin app roximation model for the nonlinear partial

diﬀerential equation characterizing the disturbance velocity potential at

the compressor inlet proposed by Moore and Greitzer [319]. Speciﬁcally,

we consider the basic compression system sh own in Figure 9.3 consisting

of an inlet duct, a compressor, an outlet duct, a plenum, and a control

throttle. We assume that the plenum dimensions are large as compared to

the compressor-duct dimensions so that the ﬂu id velocity and acceleration

in the plenum are negligible. In this case, the pressure in the plenum is

spatially uniform. Furthermore, we assume that the ﬂow is controlled by

a thr ottle at th e plenum exit. Finally, we assume a low-speed compression

system with oscillation frequencies much lower than the acoustic resonance

frequencies so that the ﬂow can be considered incompressible. However, we

do assume that the gas in the plenum is compressible, and therefore acts as

a gas spring.

- -

, V

 -

Compressor





Plenum





Throttle

Figure 9.3 Compressor system geometry.

Invoking a momentum balance across the compression system, con-

servation of mass in the plenum, and using a Galerkin projection based

on a one-mode circumferential spatial harmonic approximation for the non-

axisymmetric ﬂow disturbances yields [319]

A(t) =

3π

2π

(Φ(t) + A(t) sin θ) sin θ dθ, A(0) = A

, t ≥ 0, (9.183)

Φ(t) = −Ψ (t) +

2π

(Φ(t) + A(t) sin θ) dθ, Φ(0) = Φ

, (9.184)

Ψ(t) =

(Φ(t) −Φ

(t)), Ψ(0) = Ψ

, (9.185)

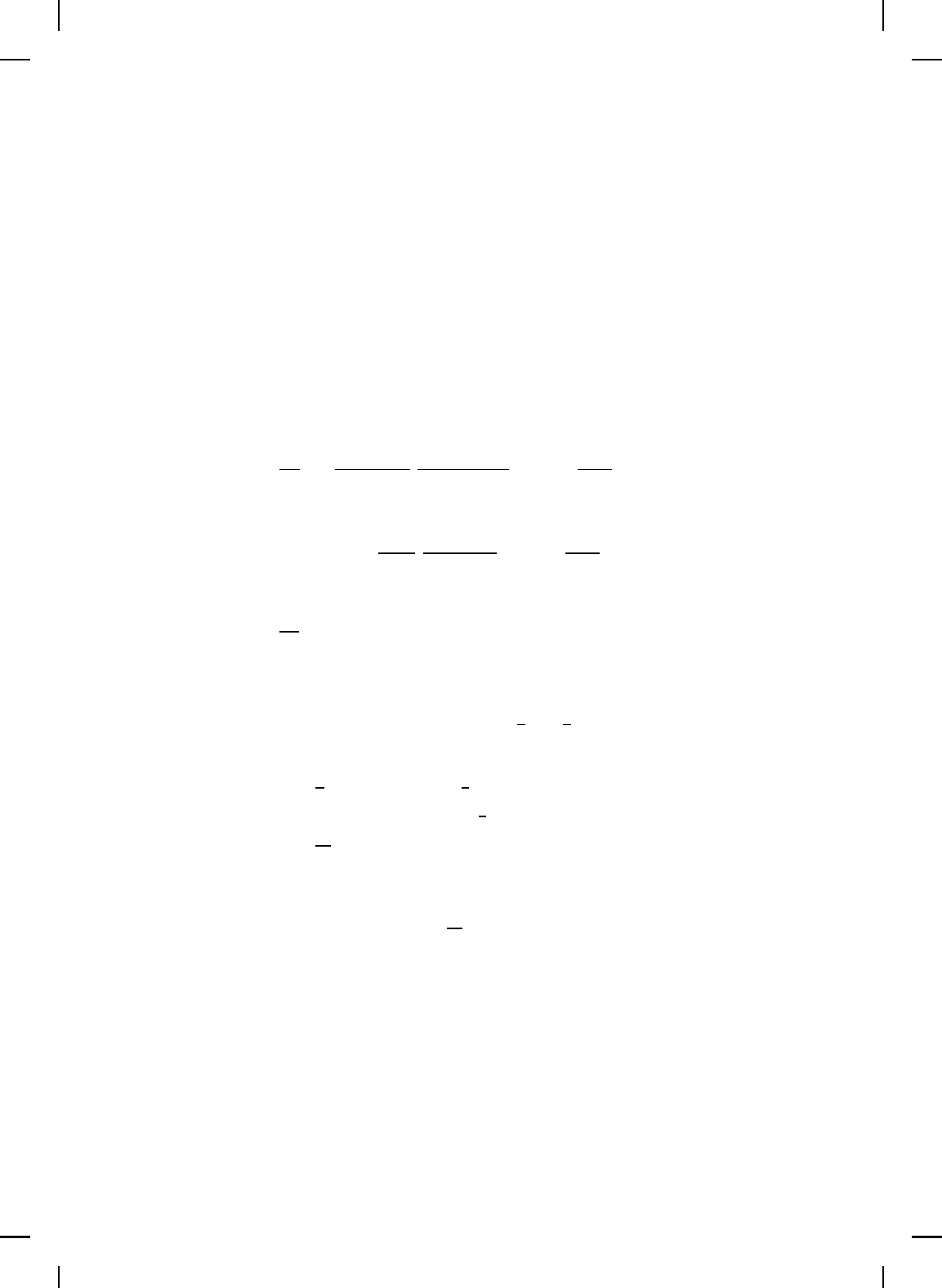
NonlinearBook10pt November 20, 2007

584 CHAPTER 9

where Φ is the circumferentially averaged axial mass ﬂow in the compressor,

Ψ is the total-to-static pressure rise, A is the normalized stall cell amplitude

of angular variation capturing a measure of nonuniformity in the ﬂow, Φ

the mass ﬂow through the throttle, σ, β are positive constant parameters,

and Ψ

(·) is a given compressor pressure-ﬂow map. The compliance

co eﬃcient β is a function of the compressor rotor speed and plenum size.

For large values of β a surge limit cycle can occur, while rotating stall can

occur for any value of β.

Now, assuming that the compressor pressure-ﬂow map Ψ

(·) is

analytic, the integral terms in (9.183)–(9.185) can be expressed in terms

of an inﬁnite Taylor series expansion about the circumferentially averaged

ﬂow to give

A(t) =

2σ

∞

k=1

k!(k − 1)!

2k− 1

(ξ)

dξ

2k− 1



ξ=Φ(t)



A(t)



2k− 1

A(0) = A

, t ≥ 0, (9.186)

Φ(t) = −Ψ(t) +

∞

k=0

(k!)

(ξ)

dξ



ξ=Φ(t)



A(t)



, Φ (0) = Φ

(9.187)

Ψ(t) =

(Φ(t) −Φ

(t)), Ψ(0) = Ψ

. (9.188)

The speciﬁc compressor pressure-ﬂow performance map Ψ

which was

considered in [319] is

(Φ) = Ψ

+ 1 +

Φ −

, (9.189)

where Ψ

is a constant parameter. In this case, (9.186)–(9.188) become

A(t) =

A(t)(1 −Φ

(t) −

(t)), A(0) = A

, t ≥ 0, (9.190)

Φ(t) = −Ψ (t) + Ψ

(Φ(t)) −

Φ(t)A

(t), Φ(0) = Φ

, (9.191)

Ψ(t) =

(Φ(t) − Φ

(t)), Ψ(0) = Ψ

. (9.192)

Next, deﬁne the control variable

△

(Φ

− Φ) (9.193)

so that for ﬁ xed values of ﬂow through the throttle, Φ

(t) ≡ Φ

Teq

, (9.190)–

(9.192) have an equilibrium point given by

, Φ

, Ψ

) = (0, Φ

Teq

, Ψ

(Φ

)). (9.194)

Deﬁning the shifted state variables x

△

= A, x

△

= Φ − Φ

, and x

△

= Ψ −

, so that for a given equilibrium point on the axisymmetric branch of

the compressor characteristic pressure-ﬂow map the sys tem equilibrium is