Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 545

where ˆx

△

= [x

, x

]

△

= R



2σp

+ R

(

σ + r)

−(p

σ + p

−(p

σ + p

r) 2p



, (8.161)

and

△



(

σ + r) −p



. (8.162)

Since 2p

is nonnegative for all θ ∈ (0, 1) it follows that (8.160) is

equivalent to (1 −θ

)Q ≥ yy

, wh ich implies that, if Q is invertible, (8.119)

is satisﬁed for all θ ∈ (0, 1) such that 1−θ

≥ y

−1

y. Hence, the maximum

possible θ such that (8.119) holds is given by

θ =

1 − y

−1

y. (8.163)

Now, it follows from Theorem 8.6 that for all p

, p

, R

> 0, such that

det Q 6= 0, with φ(x) given above the nonlinear system (8.80)–(8.82) has

disk margins of (

1+θ

1−θ

), where θ is given by (8.163). Furthermore, for

given p

, p

, and R

> 0 these disk margins are the maximum possible disk

margins that are guaranteed by Theorem 8.6. Next, we vary p

, p

, and

such that θ given by (8.163) is maximized. It can be shown that the

maximum is achieved at

and

= 0 so that

max

√

r + 1

. (8.164)

In this case, the control law φ(x) is given by φ(x) = −2rx

Next, using the control Lyapu nov function V (x) = p

+ p

where p

, p

> 0 are such that

, we design a meaningful inverse

optimal controller us ing the feedback controller given by (8.155). Using

the initial conditions (x

, x

) = (−20, −20, 30), the data parameters

σ = 10, r = 15, b = 8/3, and design parameters p

= 1.5 and p

= 1

the inverse optimal controller φ(x) = −2rx

and the meaningful inverse

optimal controller given by (8.155) were used to compare closed-loop system

performance. First, we note that the downside disk and sector margins of

the inverse optimal controller are 0.8 while the meaningful inverse optimal

controller guarantees the standard 0.5 downside sector margin with no disk

margin guarantees. Hence, both controllers have guaranteed robustness

sector margins to actuator saturation nonlinearities with, as expected, the

meaningful inverse optimal controller having a slightly larger guarantee.

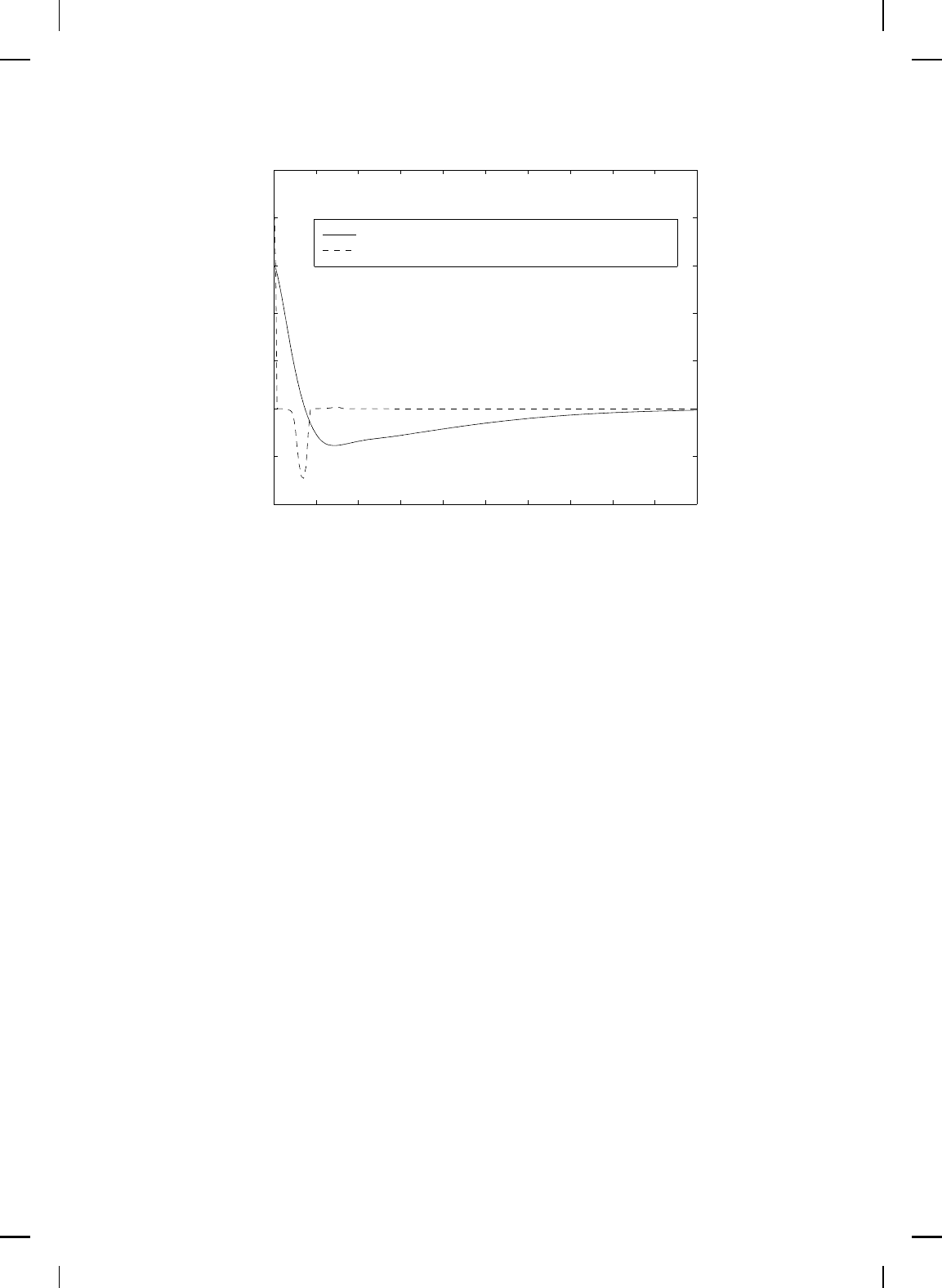
However, as shown in Figures 8.2 and 8.3, the inverse optimal controller with

a cross-weighting term in the performance functional has better transient

performance in terms of peak overshoot over the meaningful inverse optimal

controller. (We note that the controlled third state is not shown since it

is virtually identical for both designs.) Finally, Figure 8.4 compares the

NonlinearBook10pt November 20, 2007

546 CHAPTER 8

control eﬀort versus time for both controllers. △

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

-20

-15

-10

-5

First State

Time

Inverse optimal controller

Meaningful inverse optimal controller

Figure 8.2 First state versus time.

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

-20

-15

-10

-5

Second State

Time

Inverse optimal controller

Meaningful inverse optimal controller

Figure 8.3 Second state versus time.

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 547

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

-400

-200

200

400

600

800

1000

Control Effort

Time

Inverse optimal controller

Meaningful inverse optimal controller

Figure 8.4 Control eﬀort versus time.

8.9 Problems

Problem 8. 1. Show that every 2nth-order positive deﬁnite polynomial

function of the f orm V (x) =

q=1

, where P

> 0 and P

≥ 0,

q = 2, . . . , n, can be written as a q-multilinear function where q is even. Can

every multilinear function be written as a polynomial function?

Problem 8.2. Let A ∈ R

n×n

. Show that e

(

⊕A)

= (e

)

[q]

. I f, in

addition, d et A 6= 0, show

(

⊕As)

ds = (

⊕ A)

−1

(

⊕At)

− I

]. (8.165)

Finally, if α(A) < 0, show

∞

(

⊕As)

ds = −(

⊕ A)

−1

. (8.166)

Problem 8.3. Consider the nonlinear dynamical system (8.38) an d let

V : D → R be a continuously diﬀerentiable function satisfying (8.41) and

(8.42). Then we say th at the feedback control law φ : D → Ω is optimal

with respect to V if

′

(x)F (x, φ(x)) ≤ V

′

(x)F (x, u), x ∈ D, u ∈ Ω. (8.167)

NonlinearBook10pt November 20, 2007

548 CHAPTER 8

Now, consider the linear controlled system

˙x(t) = Ax(t) + Bu(t), x(0) = x

, t ≥ 0, (8.168)

where x ∈ R

and u ∈ Ω

△

= {u ∈ R

: kuk

≤ 1}, where p = 1, 2, ∞.

Assume A is Hurwitz and deﬁne V (x) = x

P x, where P ∈ R

n×n

is the

unique positive-deﬁnite solution to

0 = A

P + P A + R, (8.169)

for a given n ×n positive-deﬁnite matrix R. Furthermore, let V (x) = x

P x

be the Lyapun ov function f or the closed-loop system (8.168) with u = φ(x).

For each value of p ∈ {1, 2, ∞}, construct a feedback control law u = φ(x)

that is optimal with respect to V (·) or, equivalently, gives a maximum time

decay rate of V (x).

Problem 8.4. Consider the algebraic Riccati equation (8.53) with R

= E

≥ 0. Show that the following statements are equivalent:

i) (A, B) is stabilizable and (A, E

) is detectable.

ii) There exists a nonnegative-deﬁnite solution P satisfying (8.53) and

A−BR

−1

P is Hu rwitz.

In addition, show that the following statements hold:

iii) If (A, E

) is detectable, then P is the only nonnegative-deﬁnite solution

to (8.53).

iv) If R

> 0, then P > 0.

Problem 8.5. Consider the linear controlled system (8.51) with quad-

ratic performance functional (8.52) and R

= I

. S how that if (A, B) is

controllable, −A is Hurwitz, and R

= 0, then

P =



∞

−At

−A



−1

(8.170)

is a positive-deﬁnite solution to (8.53).

Problem 8.6. Consider the linear controlled system (8.51). Let R

∈

, R

∈ P

, α > 0, and assume there exists a positive-deﬁnite matrix

P ∈ R

n×n

such that

0 = (A + αI

)

P + P (A + αI

) + R

− P BR

−1

P. (8.171)

Show that th e linear controlled system (8.51) with feedback control law

u(t) = −R

−1

P x(t), (8.172)

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 549

has the property that all the eigenvalues of the closed-loop system have

real part less than −α. Finally, show that the stabilizing controller (8.172)

minimizes

J(x

, u(·)) =

∞

2αt

(t)R

x(t) + u

(t)R

u(t)]dt. (8.173)

Problem 8.7. Consider the nonlinear dynamical system G given by

˙x(t) = f(x(t)) + G(x(t))u(t), x(0) = x

, t ≥ 0, (8.174)

y(t) = h(x(t)), (8.175)

where x ∈ R

, u, y ∈ R

, f : R

→ R

satisﬁes f(0) = 0, G : R

→ R

n×m

and h : R

→ R

satisﬁes h(0) = 0. Assume that G is passive, zero-

state observable, and completely reachable with a continuously diﬀerentiable

radially unbounded storage fu nction V

: R

→ R. Furtherm ore, let

V : R

→ R be a continuously diﬀerentiable function such that V (0) = 0,

V (x) > 0, x ∈ R

, x 6= 0, V (x) → ∞ as kxk → ∞, and

0 = L

(x) + V

′

(x)f(x) −

′

(x)G(x)R

−1

(x)V

′T

(x), x ∈ R

, (8.176)

where L

(x) = ℓ

(x)ℓ(x) + h

(x)R

−1

h(x) and ℓ(·) satisﬁes (5.115). Show

that the output feedback controller u(t) = −R

−1

y(t), where R

> 0,

asymptotically stabilizes (8.174) and minimizes th e performance criterion

J(x

, u(·)) =

∞

[ℓ

(x(t))ℓ(x(t)) + h

(x(t))R

−1

h(x(t)) + u

(t)R

u(t)]dt,

(8.177)

in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), x

∈ R

. (8.178)

Furth ermore, show that J(x

, φ(x(·))) = V (x

), x

∈ R

Problem 8.8. Consider the nonlinear oscillator

˙x

(t) = x

(t), x

(0) = x

, t ≥ 0, (8.179)

˙x

(t) = −x

(t) + x

(t)sinh(x

(t) + x

(t)) + u(t), x

(0) = x

. (8.180)

Find a globally stabilizing feedback controller u(t) = φ(x(t)) that minimizes

J(x

, x

, u(·)) =

∞

(t) + u

(t)]dt. (8.181)

Compare the state r esponse and the control eﬀort of the optimal controller to

the feedback linearizing control law u

(t) = −x

(t)[1+ sinh(x

(t) + x

(t))].

Problem 8.9. Consider the nonlinear oscillator

˙x

(t) = x

(t), x

(0) = x

, t ≥ 0, (8.182)

NonlinearBook10pt November 20, 2007

550 CHAPTER 8

˙x

(t) = −e

(t)[x

(t)+

(t)]

(t)e

(t)+3x

(t)

+ e

(t)+2x

(t)

u(t),

(0) = x

. (8.183)

Find a stabilizing feedb ack controller u(t) = φ(x(t)) that minimizes

J(x

, x

, u(·)) =

∞

(t) + u

(t)]dt. (8.184)

Is your controller a global stabilizer?

Problem 8.10. Consider the nonlinear dynamical system

˙x

(t) = −x

(t) + x

(t)x

(t), x

(0) = x

, t ≥ 0, (8.185)

˙x

(t) = −x

(t) + x

(t)u(t), x

(0) = x

. (8.186)

Find a stabilizing feedb ack controller u(t) = φ(x(t)) that minimizes

J(x

, x

, u(·)) =

∞

[2x

(t) + 2x

(t) +

(t)]dt. (8.187)

Problem 8.11. Show that in the case w here 0 < r ≤ 1, the

uncontrolled (u(t) ≡ 0) Lorentz dynamical system (8.80)–(8.82) has only

one equilibrium state, namely, x

△

= (0, 0, 0)

. Alternatively, show that

in the case where r > 1, the uncontrolled Lorentz dynamical system

(8.80)–(8.82) has three equilibrium states, namely, x

, x

△

= (

b(r − 1),

b(r − 1), r − 1)

, and x

△

= (−

b(r − 1), −

b(r − 1), r − 1)

. Finally,

show that if r ≤ 1, x

is a locally asymptotically stable equilibrium point

while if r > 1, x

is unstable. What can you say about the stability of x

and x

Problem 8.12. Using Theorem 8.3 construct a globally asymp totically

stabilizing control law for the equilibrium state x

△

= (

b(r − 1),

r − 1)

, r > 1, of the controlled Lorentz dynamical system (8.80)–(8.82).

Problem 8.13. Consider the nonlinear controlled system (8.56) with

performance functional (8.58). Assume there exists a continuously diﬀer-

entiable function V : R

→ R and a function L

: R

→ R

1×m

such that

(8.59)–(8.61) and (8.63) hold, and

′

(x)f

(x) ≤ 0, x ∈ R

, (8.188)

△

= {x ∈ R

: L

k+1

V (x) = L

V (x) = 0, k = 0, 1, . . . , i = 1, . . . , m}

= {0}, (8.189)

where f

(x)

△

= f(x) −

G(x)R

−1

(x)L

(x). Show that, with the feedback

control law (8.65), the zero solution x(t) ≡ 0 of the closed-loop system (8.64)

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 551

is globally asymptotically stable, and the perf ormance functional (8.58) w ith

(x) given by (8.66) is minimized in the sense that (8.67) and (8.68) hold.

Problem 8.14. Assume the controlled system (8.56) with output

y(t) = h(x(t)), where h : R

→ R

, is minimum phase with relative

degree {1, 1, . . . , 1} and complete and involutive vector ﬁeld G(L

−1

Furth ermore, let

V (x) = V

(z) + y

P y, (8.190)

(x) = R

(x)[L

h(x)]

−1

(z, y)



∂V

(z)

∂z



+ 2L

h(x)],

(8.191)

where V

: R

n−m

→ R is a continuously diﬀerentiable positive-deﬁnite

function such that V

(0) = 0, V

′

(z)f

(z) < 0, z ∈ Z

△

= {x ∈ R

: h(x) = 0},

and ˙z = f

(z), and where P is an arbitrary m × m positive-deﬁnite matrix

and r(z, y) is deﬁned as in Lemma 6.2. Show that the feedback control law

φ(x) = −

h(x)]

−1

(z, y)



∂V

(z)

∂z



+ 2L

h(x)]

−R

−1

(x)[L

h(x)]

P h(x), (8.192)

globally asymptotically stabilizes (8.56) and minimizes the performance

functional (8.58) with L

(x) given by (8.66) in the sense that (8.67) and

(8.68) hold.

Problem 8.15. Consider the nonlinear dynamical system representing

a controlled rigid spacecraft with one torque input given by

˙x

(t) = I

(t)x

(t) +

u(t), x

(0) = x

, t ≥ 0, (8.193)

˙x

(t) = I

(t)x

(t) +

u(t), x

(0) = x

, (8.194)

˙x

(t) = I

(t)x

(t) +

u(t), x

(0) = x

, (8.195)

where I

= (I

−I

)/I

, I

= (I

−I

)/I

, I

= (I

−I

)/I

, and I

, I

, and

are principal moments of inertia of the spacecraft. Using Problem 8.13

with V (x) =

+ I

) and L

(x) = 0, where x = [x

]

construct a globally stabilizing controller for (8.193)–(8.195).

Problem 8.16. Consider the nonlinear dynamical system

˙x

(t) = u

(t), x

(0) = x

, t ≥ 0, (8.196)

˙x

(t) = u

(t), x

(0) = x

, (8.197)

˙x

(t) = x

(t)x

(t), x

(0) = x

, (8.198)

representing a controlled rigid spacecraft with two actuators along the

principal axes and whose uncontrolled principal axis is not an axis of

NonlinearBook10pt November 20, 2007

552 CHAPTER 8

symmetry. Using Problem 8.14 with

(t) = x

(t) + αx

(t), (8.199)

(t) = x

(t) + βx

k+1

(t), (8.200)

where k is a positive integer and α, β are arbitrary real numbers, construct

a globally stabilizing controller for (8.196)–(8.198).

Problem 8.17. Prove Theorem 8.10.

Problem 8.18. Consider the port-controlled Hamiltonian system given

by (6.22) with performance functional (8.58). Assume that there exist

functions H

, H

: D → R, J

, J

: D → R

n×n

, R

: D → R

n×n

such

that H

(x) = H(x) + H

(x) is continuously diﬀerentiable, J

(x) = J(x) +

(x), J

(x) = −J

(x), R

(x) = R(x)+R

(x), R

(x) = R

(x) ≥ 0, x ∈ D,

condition (6.25) is satisﬁed, and

∂

∂x

(x) > 0, x ∈ D, (8.201)

(x) − R

(x) +

G(x)R

−1

(x)G

(x)]



∂H

∂x

(x)



= [−[J

(x) − R

(x)]

−

G(x)R

−1

(x)G

(x)]



∂H

∂x

(x)



−

G(x)R

−1

(x)L

(x), x ∈ D.

(8.202)

Show that the equ ilibr ium solution x(t) ≡ x

of th e closed-loop system given

by (6.24) is Lyapunov stable with the feedback control law

φ(x) = −

−1

(x)



∂H

∂x

(x)



+ L

(x)

, x ∈ D. (8.203)

If, in addition, D

⊆ D is a compact positively invariant set with respect

to (6.24) and the largest invariant set contained in R

△

= {x ∈ D

∂H

∂x

(x)R

(x)



∂H

∂x

(x)



= 0} is M = {x

}, show that the equilibrium

solution x(t) ≡ x

of the closed-loop system (6.24) is locally asymptotically

stable. Moreover, show that the performance functional (8.58), with

(x) = φ

(x)R

(x)φ(x) −

∂H

∂x

(x) [J(x) − R(x)]



∂H

∂x

(x)



, (8.204)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈C(x

)

J(x

, u(·)), x

∈ D

, (8.205)

and J(x

, φ(x(·))) = H

) − H

), x

∈ D

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 553

Problem 8.19. Consider the nonlinear d ynamical system G given

by (8.100) and assume that G is a J-Q type system (see Problem 6.25)

so that there exists a continuously diﬀerentiable positive-deﬁnite, radially

unbounded function V : R

→ R satisfying i) an d ii) of Problem 6.25. Show

that with the feedback stabilizing control law

φ(x) = −κ[V

′

(x)G(x)]

, κ > 0, (8.206)

the nonlinear system (8.100) and (8.101) has a disk margin (0, ∞). Further-

more, with the feedback control law u = φ(x), show that the performance

functional

J(x

, u(·)) =

∞



′

(x(t))G(x(t))][V

′

(x(t))G(x(t))]

−V

′

(x(t))f(x(t)) +

(t)u(t)



dt, (8.207)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), x

∈ R

. (8.208)

Problem 8.20. Consider the nonlinear dynamical system G given by

(8.100) and let V : R

→ R be a continuously diﬀerentiable positive-deﬁnite,

radially unbounded control L yapunov function for (8.100). Let φ : R

→ R

satisfy

kφ(x)k = min{kuk : V

′

(x)[f(x) + G(x)u] ≤ −σ(x), u ∈ R

}, x ∈ R

(8.209)

where k · k denotes the Euclidean norm, σ : R

→ R is a continuous

positive-deﬁnite function such that V

′

(x)f(x) ≤ −σ(x), x ∈ R

△

= {x ∈

: V

′

(x)G(x) = 0}. Show that the control law φ(x) given by (8.209) is

globally stabilizing and inverse optimal with respect to the cost functional

J(x

, u(·)) =

∞

(x(t)) + u

(t)R

(x(t))u(t)]dt, (8.210)

where L

(x) ≥ 0 and R

(x) > 0, x ∈ R

. If, in addition,

σ(x) =

(x) + q(x)β

(x)β(x),

where α(x)

△

= V

′

(x)f(x), β(x)

△

= V

′

(x)G(x), and q : R

→ R is a

nonnegative function, show that the control law φ(x) given by (8.209)

specializes to

φ(x) =

(

−

α(x)+

√

(x)+q(x)β

(x)β(x)

β(x), β(x) 6= 0,

0, β(x) = 0.

(8.211)

Finally, let κ : R → R be a continuously diﬀerentiable class K function and

let

V : R

→ R be a continuously diﬀerentiable positive-deﬁnite, radially

NonlinearBook10pt November 20, 2007

554 CHAPTER 8

unbounded fun ction such that V (x) = κ(

V (x)) and

0 =

′

(x)f(x) + q(x) −

′

(x)G(x)G

(x)

′T

(x). (8.212)

Show th at the control law u = φ(x) given by (8.211) minimizes the cost

functional

J(x

, u(·)) =

∞

[q(x(t)) + u

(t)u(t)]dt. (8.213)

Problem 8.21. Consider the port-controlled Hamiltonian s ystem

˙x(t) = J(x(t))



∂H

∂x

(x(t))



+ G(x(t))u(t), x(0) = x

, t ≥ 0, (8.214)

y(t) = G

(x(t))



∂H

∂x

(x(t))



, (8.215)

where x ∈ R

, u, y ∈ R

, H : D → R, G : R

→ R

n×m

, and J : R

→

n×n

satisﬁes J(x) = −J

(x). Assume that (8.214) an d (8.215) is zero-

state observable. Sh ow that the feedback control law φ(x) = −G

(x)



∂H

∂x



asymptotically stabilizes (8.214) and minimizes th e perf orman ce functional

J(x

, u(·)) =

∞

(t)y(t) + u

(t)u(t)]dt. (8.216)

8.10 Notes and References

The results in Sections 8.2 and 8.3 on stability analysis and optimal control

of nonlinear systems are due to Bernstein [43]. In particular, Bernstein [43]

gives an excellent review of the nonlinear-nonquadratic control problem in

a simpliﬁed and tutorial manner. Polynomial forms in the performance

criterion were developed by Speyer [411] while multilinear forms were

addressed by Bass and Webber [33]. A treatment of nonlinear-nonquadratic

optimal control is also given by Jacobson [217]. T he invers e optimal control

problem has been studied by numerous authors including Kalman [227],

Moylan and Anderson [321], Moylan [320], Molinari [317], Jacobson [217],

Anderson and Moore [10], Wan and Bernstein [449], and m ore recently by

Freeman and Kokotovic [127,128]. The presentation here parallels that given

by Wan and Bernstein [449].

The equivalence between optimality and passivity is d ue to Kalman

[227] for linear systems and Moylan [320] for nonlinear s ystems. Gain,

sector, and disk margins of nonlinear-nonquadratic optimal regulators

with performance measures involving cross-weighting terms are due to

Chellaboina and Haddad [85]. An excellent treatment on m eaningful inverse

optimality is given by Freeman and Kokotovi´c [128] and Sepulchre, Jankovi´c,

and Kokotovi´c [395].