Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 515

and uniqueness of speciﬁc multilinear forms. A scalar f unction ψ : R

→ R

is q-multilinear if q is a positive integer and ψ(x) is a linear combination

of terms of the form x

···x

, where i

is a nonnegative integer for

j = 1, . . . , n, and i

+···+ i

= q. Furthermore, a q-multilinear function

ψ(·) is nonnegative deﬁnite (respectively, positive deﬁnite) if ψ(x) ≥ 0 for

all x ∈ R

(respectively, ψ(x) > 0 for all nonzero x ∈ R

). Note that if q is

odd then ψ(x) cannot be positive deﬁnite. If ψ(·) is a q-multilinear function,

then ψ(·) can be repr esented by means of Kronecker products, that is, ψ(x)

is given by ψ(x) = Ψx

[q]

, where Ψ ∈ R

1×n

The following lemma due to Bernstein [43] is needed for several of

the main results of this book. For this result deﬁne the spectral abscissa of

A ∈ R

n×n

α(A)

△

= max{Re λ : λ ∈ spec(A)}.

We say that th e matrix A ∈ R

n×n

is Hurwitz if and only if α(A) < 0.

Lemma 8.1. Let A ∈ R

n×n

be Hurw itz and let h : R

→ R be a

q-multilinear function. Then there exists a unique q-multilinear function

g : R

→ R such that

0 = g

′

(x)Ax + h(x), x ∈ R

. (8.19)

Furth ermore, if h(x) is nonnegative (respectively, positive) deﬁnite, then

g(x) is nonnegative (respectively, positive) deﬁnite.

Proof. Let h(x) = Ψx

[q]

and deﬁne g(x)

△

= Γ x

[q]

, where Γ

△

= −Ψ(

⊕

−1

. Note that

⊕ A is invertible since A is Hurwitz. Now, note that for

all x ∈ R

′

(x)Ax = Γ

[q]

)Ax

= Γ (x ⊗··· ⊗ I + x ⊗ ··· ⊗ I ⊗ x + ··· + I ⊗··· ⊗ x) Ax

= Γ (x ⊗··· ⊗ Ax + x ⊗ ··· ⊗Ax ⊗x + ··· + Ax ⊗ ··· ⊗ x)

= Γ (I ⊗ ··· ⊗A + I ⊗ ···⊗ A ⊗I + ··· + A ⊗I ··· ⊗ I) x

[q]

= Γ (A ⊕A ⊕ ···⊕ A) x

[q]

= Γ(

⊕ A)x

[q]

= −Ψx

[q]

= −h(x).

To prove uniquen ess, suppose that ˆg(x) =

Γx

[q]

satisﬁes (8.19). Then

it follows that

Γ(

⊕ A)x

[q]

Γ(

⊕ A)x

[q]

NonlinearBook10pt November 20, 2007

516 CHAPTER 8

Since

⊕ A is Hurwitz and e

(

⊕A)t

= (e

)

[q]

, it follows that, for all x ∈ R

Γx

[q]

= Γ(

⊕ A)(

⊕ A)

−1

[q]

= −Γ(

⊕ A)

∞

(

⊕A)t

[q]

= −Γ(

⊕ A)

∞

)

[q]

= −Γ(

⊕ A)

∞

[q]

= −

Γ(

⊕ A)

∞

[q]

Γx

[q]

which shows that g(x) = ˆg(x), x ∈ R

Finally, if h(x) is nonnegative deﬁnite, then it follows that for all

x ∈ R

g(x) = −Ψ(

⊕ A)

−1

[q]

= Ψ

∞

(

⊕A)t

[q]

dt = Ψ

∞

[q]

dt ≥ 0.

If, in addition, x 6= 0, then e

x 6= 0, t ≥ 0. Hence, if h(x) is positive

deﬁnite, then g(x) is positive deﬁnite.

Next, assume A is Hurwitz, let P be given by (8.12), and consider the

case in which L(·), f(·), and V (·) are given by

L(x) = x

Rx + h(x), (8.20)

f(x) = Ax + N(x), (8.21)

V (x) = x

P x + g(x), (8.22)

where h : D → R and g : D → R are nonquadratic, and N : D → R

nonlinear. In this case, (8.6) holds if and only if

0 = x

Rx+h(x)+x

P +P A)x+2x

P N(x)+g

′

(x)(Ax+N(x)), x ∈ D,

(8.23)

or, equivalently,

0 = x

P + P A + R)x + g

′

(x)(Ax + N(x)) + h(x) + 2x

P N(x), x ∈ D.

(8.24)

Since A is Hurwitz, we can choose P to satisfy (8.12) as in the linear-

quadratic H

case. Now, suppose N(x) ≡ 0 and let P satisfy (8.12). Then

(8.24) specializes to

0 = g

′

(x)Ax + h(x), x ∈ D. (8.25)

Next, given h(·), we determine th e existence of a function g(·) satisfying

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 517

(8.25). Here, we focus our attention on multilinear functionals for wh ich

(8.25) holds with D = R

. Speciﬁcally, let h(x) be a nonnegative-deﬁnite

q-multilinear function, where q is n ecessarily even. Furthermore, let g(x) be

the nonnegative-deﬁnite q-multilinear function given by Lemma 8.1. Then,

since g

′

(x)Ax ≤ 0, x ∈ R

, it follows that x

P x + g(x) is a Lyapunov

function f or (8.10). Hence, Lemma 8.1 can be used to generate Lyapunov

functions of speciﬁc multilinear structures.

To demonstrate the above discussion suppose h(x) in (8.20) is of the

more general form given by

h(x) =

ν=2

2ν

(x), (8.26)

where, for ν = 2, 3, . . . , r, h

2ν

: R

→ R is a nonnegative-deﬁnite 2ν-multilin-

ear function. Now, us ing Lemma 8.1, it follows that there exists a nonnegati-

ve-deﬁnite 2ν-multilinear function g

2ν

: R

→ R satisfying

0 = g

′

2ν

(x)Ax + h

2ν

(x), x ∈ R

, ν = 2, 3, . . . , r. (8.27)

Deﬁning g(x)

△

ν=2

2ν

(x) and summing (8.27) over ν yields (8.25). Since

(8.6) is satisﬁed with L(x) and V (x) given by (8.20) and (8.22), respectively,

(8.7) implies that

J(x

) = x

P x

+ g(x

). (8.28)

To illustrate condition (8.25) with quartic Lyapunov functions let

V (x) = x

P x + (x

Mx)

, (8.29)

where P satisﬁes (8.12) and assume M is an n ×n symmetric matin. In this

case, g(x) = (x

Mx)

is a nonnegative-deﬁnite 4-multilinear function and

(8.25) yields

h(x) = −2(x

Mx)x

M + MA)x. (8.30)

Now, letting M satisfy

0 = A

M + MA +

R, (8.31)

where

R is an n × n symmetric matrix, it follows from (8.30) that h(x)

satisfying (8.25) is of the form

h(x) = 2(x

Mx)(x

Rx). (8.32)

R is nonnegative deﬁnite, then M is nonnegative deﬁnite, and hence, h(x)

is a nonnegative-deﬁnite 4-multilinear function. Thus, if V (x) is a quartic

Lyapunov function of the form given by (8.29), and L(x) is given by

L(x) = x

Rx + 2(x

Mx)(x

Rx), (8.33)

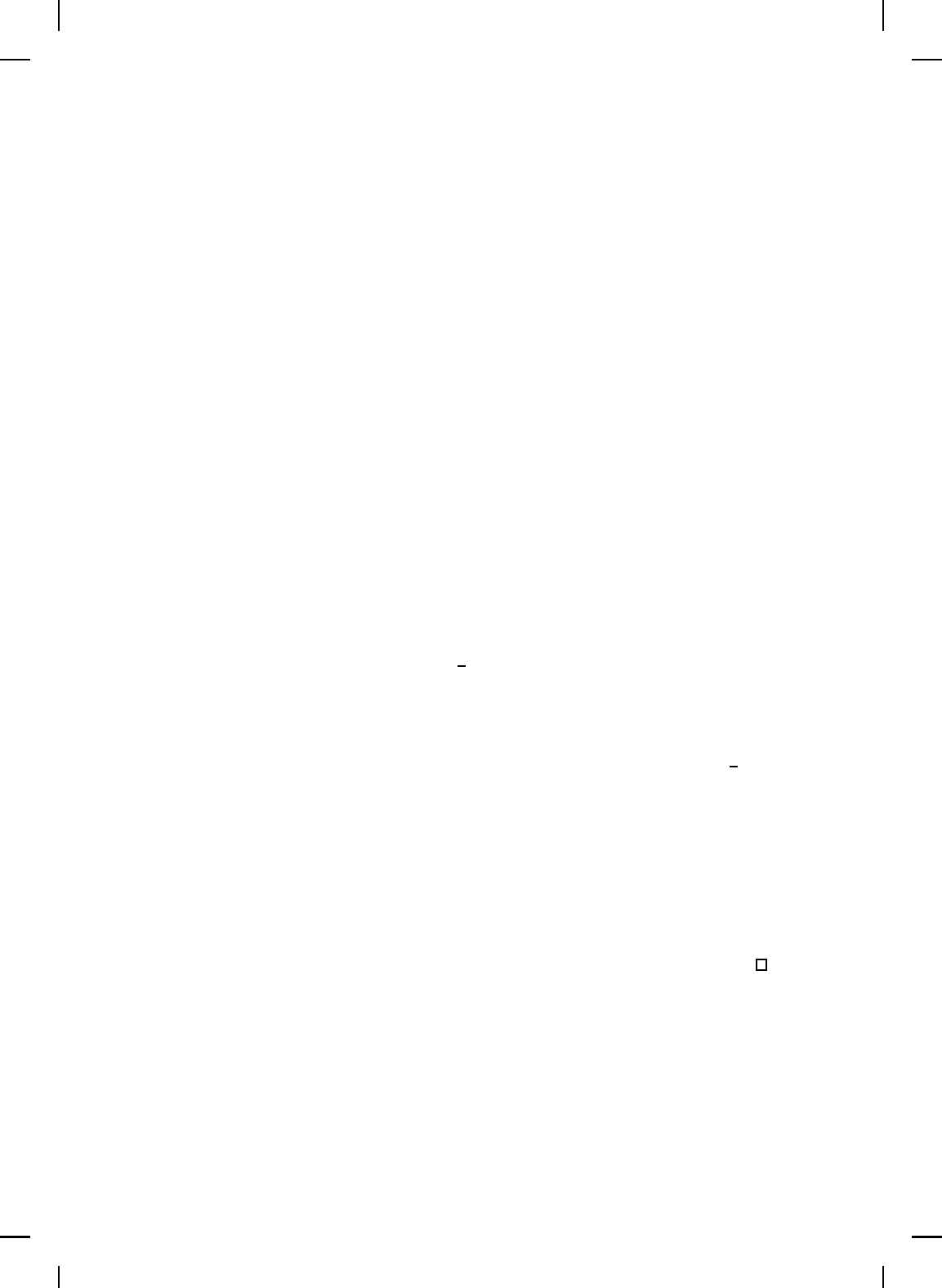
NonlinearBook10pt November 20, 2007

518 CHAPTER 8

where M satisﬁes (8.31), then cond ition (8.25), and hence, (8.6), is satisﬁed.

The follow ing proposition generalizes the above results to general polynomial

cost functionals.

Proposition 8.1. Let A ∈ R

n×n

be Hurwitz, R ∈ R

n×n

, R > 0, and

∈ R

n×n

≥ 0, q = 2, . . . , r. Consider the linear system (8.10) with

performance functional

J(x

)

△

∞







(t)Rx(t) +

q=2

(t)

x(t))(x

(t)M

x(t))

q−1







dt,

(8.34)

where M

∈ R

n×n

, M

≥ 0, q = 2, . . . , r, satisfy

0 = A

+ M

A +

. (8.35)

Furth ermore, assume there exists a positive-deﬁnite matrix P ∈ R

n×n

such

that

0 = A

P + P A + R. (8.36)

Then the zero solution x(t) ≡ 0 to (8.10) is globally asymptotically stable

and

J(x

) = x

P x

q=2

)

, x

∈ R

. (8.37)

Proof. The result is a direct consequence of Theorem 8.1 with f (x) =

Ax, L(x) = x

Rx+

q=2

[(x

x)(x

q−1

], V (x) = x

P x+

q=2

, and D = R

. Speciﬁcally, conditions (8.3) and (8.4) are trivially

satisﬁed. Now,

′

(x)f(x) = x

P + P A)x +

q=2

q−1

, M

+ M

A)x,

and hence, it follows from (8.35) and (8.36) that L(x) + V

′

(x)f(x) = 0,

x ∈ R

, s o that all the conditions of Theorem 8.1 are satisﬁed. Finally,

since V (·) is radially unbounded (8.10) is globally asymptotically stable.

Proposition 8.1 requires the solutions of r − 1 Lyapu nov equations

in (8.35) to obtain a closed-form expression for the nonlinear-nonquadratic

cost functional (8.34). However, if

, q = 3, . . . , r, then M

= M

q = 3, . . . , r, satisﬁes (8.35). In this case, the solution of only one Lyapunov

equation in (8.35) is required.

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 519

8.3 Optimal Nonlinear Control

In this section, we consider a control problem involving a notion of optimality

with respect to a nonlinear-nonquadratic cost functional. The optimal

feedback controllers are d erived as a direct consequence of Theorem 8.1.

To address the optimal control problem let D ⊆ R

be an open set and let

U ⊆ R

, where 0 ∈ D and 0 ∈ U. Furthermore, let F : D×U → R

be s uch

that F (0, 0) = 0. Next, consider the controlled nonlinear dyn amical system

G given by

˙x(t) = F (x(t), u(t)), x(0) = x

, t ≥ 0, (8.38)

where u(·) is restricted to the class of admissible controls consisting of

measurable function u(·) such that u(t) ∈ U for all t ≥ 0, w here the

constraint set U is given. We assume 0 ∈ U. Given a control law φ(·)

and a feedback control u(t) = φ(x(t)), the closed-loop system shown in the

Figure 8.1 has the form

˙x(t) = F (x(t), φ(x(t))), x(0) = x

, t ≥ 0. (8.39)

φ(x)



Figure 8.1 Nonlinear closed-loop feedback system.

Next, we present a main theorem due to Bern s tein [43] for characteriz-

ing feedback controllers that guarantee stability and minimize a nonlinear-

nonquadratic performance functional. For the statement of this result let

L : D × U → R and deﬁne the s et of regulation controllers by

S(x

)

△

= {u(·) : u(·) is admissible and x(·) given by (8.38)

satisﬁes x(t) → 0 as t → ∞}.

Theorem 8.2. Consider the nonlinear controlled dynamical system

NonlinearBook10pt November 20, 2007

520 CHAPTER 8

(8.38) with performance functional

J(x

, u(·))

△

∞

L(x(t), u(t))dt, (8.40)

where u(·) is an admissible control. Assume that there exists a continuously

diﬀerentiable function V : D → R and a control law φ : D → U such that

V (0) = 0, (8.41)

V (x) > 0, x ∈ D, x 6= 0, (8.42)

φ(0) = 0, (8.43)

′

(x)F (x, φ(x)) < 0, x ∈ D, x 6= 0, (8.44)

H(x, φ(x)) = 0, x ∈ D, (8.45)

H(x, u) ≥ 0, x ∈ D, u ∈ U, (8.46)

where

H(x, u)

△

= L(x, u) + V

′

(x)F (x, u). (8.47)

Then, with the feedback control u(·) = φ(x(·)), the zero solution x(t) ≡ 0

of the closed-loop system (8.39) is locally asymptotically stable and there

exists a neighborhood of the origin D

⊆ D such that

J(x

, φ(x(·))) = V (x

), x

∈ D

. (8.48)

In addition, if x

∈ D

then the feedback control u(·) = φ(x(·)) minimizes

J(x

, u(·)) in the s en se that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)). (8.49)

Finally, if D = R

, U = R

, and

V (x) → ∞ as kxk → ∞, (8.50)

then the zero solution x(t) ≡ 0 of th e closed-loop system (8.39) is globally

asymptotically stable.

Proof. Local and global asymptotic stability are a direct consequence

of (8.41)–(8.44) and (8.50) by applying Theorem 8.1 to the closed-loop

system (8.39). Furthermore, using (8.45), condition (8.48) is a restatement

of (8.7) as applied to the closed-loop system. Next, let x

∈ D

, let

u(·) ∈ S(x

), and let x(t), t ≥ 0, be the solution of (8.38). Then it follows

that

0 = −

V (x(t)) + V

′

(x(t))F(x(t), u(t)).

Hence,

L(x(t), u(t)) = −

V (x(t)) + L(x(t), u(t)) + V

′

(x(t))F(x(t), u(t))

= −

V (x(t)) + H(x(t), u(t)).

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 521

Now, using (8.46) and the fact that u(

) ∈ S(x

), it follows that

J(x

, u(·)) =

∞

[−

V (x(t)) + H(x(t), u(t))]dt

= − lim

t→∞

V (x(t)) + V (x

) +

∞

H(x(t), u(t))dt

= V (x

) +

∞

H(x(t), u(t))dt

≥ V (x

)

= J(x

, φ(x(·)),

which yields (8.49).

Note that (8.45) is the steady-state Hamilton-Jacobi-Bellman equation

for the nonlinear system F (·, ·) with the cost J(x

, u(·)). Fu rthermore,

conditions (8.45) and (8.46) guarantee optimality with respect to the set

of admissible stabilizing controllers S(x

). However, it is important to note

that an explicit characterization of S(x

) is not required. In addition, the

optimal stabilizing feedback control law u = φ(x) is independent of the initial

condition x

. Finally, in order to ensure asymptotic stability of the closed-

loop system (8.38), Theorem 8.2 requires that V (·) satisfy (8.41), (8.42),

and (8.44), which implies that V (·) is a Lyapunov fu nction for the closed-

loop system (8.38). However, for optimality V (·) need not satisfy (8.42) and

(8.44). Speciﬁcally, if V (·) is a continuously diﬀerentiable function such th at

(8.41) is satisﬁed and φ(·) ∈ S(x

), then (8.45) and (8.46) imply (8.48) and

(8.49).

Next, we specialize Theorem 8.2 to linear systems and provide

connections to the optimal linear-quadratic regulator problem. For the

following result let A ∈ R

n×n

, B ∈ R

n×m

, R

∈ P

, and R

∈ P

given.

Corollary 8.2. Consider the linear controlled dynamical system

˙x(t) = Ax(t) + Bu(t), x(0) = x

, t ≥ 0, (8.51)

with quadratic performance functional

J(x

, u(·))

△

∞

(t)R

x(t) + u

(t)R

u(t)]dt, (8.52)

where u(·) is an admissible control. Furthermore, assume th at there exists

a positive-deﬁnite matrix P ∈ R

n×n

such that

0 = A

P + P A + R

− P BR

−1

P. (8.53)

Then, w ith th e feedback control u = φ(x)

△

= −R

−1

P x, the zero solution

NonlinearBook10pt November 20, 2007

522 CHAPTER 8

x(t) ≡ 0 to (8.51) is globally asymptotically stable and

J(x

, φ(x(·))) = x

P x

, x

∈ R

. (8.54)

Furth ermore,

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), (8.55)

where S(x

) is the set of regulation controllers for (8.51) and x

∈ R

Proof. The result is a direct consequence of Theorem 8.2 with F (x, u)

= Ax+Bu, L(x, u) = x

x+u

u, V (x) = x

P x, D = R

, and U = R

Speciﬁcally, conditions (8.41) and (8.42) are trivially satisﬁed. Next, it

follows from (8.53) that H(x, φ(x)) = 0, and hence, V

′

(x)F (x, φ(x)) < 0

for all x ∈ R

and x 6= 0. Thus, H(x, u) = H(x, u) − H(x, φ(x)) = [u −

φ(x)]

[u−φ(x)] ≥ 0 so that all the conditions of Theorem 8.2 are satisﬁed.

Finally, since V (·) is radially unbounded the zero solution x(t) ≡ 0 to (8.51)

with u(t) = φ(x(t)) = −R

−1

P x(t) is globally asymptotically s table.

The optimal feedback control law φ(x) in Corollary 8.2 is derived using

the properties of H(x, u) as deﬁned in Theorem 8.2. Speciﬁcally, since

H(x, u) = x

x + u

u + x

P + P A)x + 2x

P Bu it follows that

∂

∂u

= R

> 0. Now,

∂H

∂u

= 2R

u + 2B

P x = 0 gives the unique global

minimum of H(x, u). Hence, since φ(x) minimizes H(x, u) it follows that

φ(x) satisﬁes

∂H

∂u

= 0 or, equivalently, φ(x) = −R

−1

P x.

8.4 Inverse Optimal Control for Nonlinear Aﬃ n e Systems

In this section, we specialize Theorem 8.2 to aﬃne systems. Speciﬁcally, we

construct nonlinear f eedback controllers using an optimal control fr amework

that minimizes a nonlinear-nonquadratic perform ance criterion. This is

accomplished by choosing the controller such that the time derivative of

the Lyapunov function is negative along the closed-loop system trajectories

while providing suﬃcient cond itions for the existence of asymptotically

stabilizing solutions to the Hamilton-Jacobi-Bellman equation. Thus, these

results provide a family of globally stabilizing controllers parameterized by

the cost functional that is minimized.

The controllers obtained in this section are predicated on an inverse

optimal control problem [10, 127, 135,186, 217,218, 227, 317,320, 321, 449]. In

particular, to avoid the complexity in solving the steady-state Hamilton-

Jacobi-Bellman equation we do not attempt to min imize a given cost

functional, but rather, we parameterize a family of stabilizing controllers

that minimize some derived cost functional that provides ﬂexibility in

specifying the control law. The performance integrand is shown to explicitly

depend on the nonlinear system dynamics, the Lyapunov fu nction of the

NonlinearBook10pt November 20, 2007

OPTIMAL NONLINEAR FEEDBACK CONTROL 523

closed-loop system, and the stabilizing feedback control law, wherein the

coupling is introduced via the Hamilton-Jacobi-Bellman equation. Hence,

by varying parameters in the Lyapunov function and the performance

integrand, the proposed framework can be used to characterize a class of

globally stabilizing controllers that can meet closed-loop system response

constraints.

Consider the nonlinear aﬃne system given by

˙x(t) = f (x(t)) + G(x(t))u(t), x(0) = x

, t ≥ 0, (8.56)

where f : R

→ R

satisﬁes f (0) = 0, G : R

→ R

n×m

, D = R

, and

U = R

. Fu rthermore, we consider performan ce integrands L(x, u) of th e

form

L(x, u) = L

(x) + L

(x)u + u

(x)u, (8.57)

where L

: R

→ R, L

: R

→ R

1×m

, and R

: R

→ P

so that (8.40)

becomes

J(x

, u(·)) =

∞

(x(t)) + L

(x(t))u(t) + u

(t)R

(x(t))u(t)]dt. (8.58)

Theorem 8.3. Consider the nonlinear controlled aﬃne system (8.56)

with performance functional (8.58). Assume that there exists a continuously

diﬀerentiable fu nction V : R

→ R and a function L

: R

→ R

1×m

such

that

V (0) = 0, (8.59)

(0) = 0, (8.60)

V (x) > 0, x ∈ R

, x 6= 0, (8.61)

′

(x)[f(x) −

G(x)R

−1

(x)L

(x)

−

G(x)R

−1

(x)G

(x)V

′T

(x)] < 0, x ∈ R

, x 6= 0, (8.62)

and

V (x) → ∞ as kxk → ∞. (8.63)

Then the zero solution x(t) ≡ 0 of the closed-loop system

˙x(t) = f (x(t)) + G(x(t))φ(x(t)), x(0) = x

, t ≥ 0, (8.64)

is globally asymptotically stable with the feedback control law

φ(x) = −

−1

(x)[G

(x)V

′T

(x) + L

(x)], (8.65)

and the performan ce functional (8.58), with

(x) = φ

(x)R

(x)φ(x) −V

′

(x)f(x), (8.66)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), x

∈ R

. (8.67)

NonlinearBook10pt November 20, 2007

524 CHAPTER 8

Finally,

J(x

, φ(x(·))) = V (x

), x

∈ R

. (8.68)

Proof. The result is a direct consequence of Theorem 8.2 with D = R

U = R

, F (x, u) = f(x)+G(x)u, and L(x, u) = L

(x)+L

(x)u+u

(x)u.

Speciﬁcally, with (8.57) the Hamiltonian has the form

H(x, u) = L

(x) + L

(x)u + u

(x)u + V

′

(x)(f(x) + G(x)u).

Now, the feedback control law (8.65) is obtained by setting

∂H

∂u

= 0.

With (8.65), it follows that (8.59), (8.61), (8.62), and (8.63) imply (8.41),

(8.42), (8.44), and (8.51), respectively. Next, since V (·) is continuously

diﬀerentiable and x = 0 is a local minimum of V (·), it follows that V

′

(0) = 0,

and hence, since by assumption L

(0) = 0, it follows that φ(0) = 0,

which implies (8.43). Next, with L

(x) given by (8.66) and φ(x) given

by (8.65) and (8.45) holds. Finally, since H(x, u) = H(x, u) −H(x, φ(x)) =

[u − φ(x)]

(x)[u − φ(x)] and R

(x) is positive deﬁnite for all x ∈ R

condition (8.46) holds. T he result now follows as a direct consequence of

Theorem 8.2.

Note that (8.62) is equivalent to

V (x)

△

= V

′

(x)[f(x) + G(x)φ(x)] < 0, x ∈ R

, x 6= 0, (8.69)

with φ(x) given by (8.65). Fu rthermore, conditions (8.59), (8.61), and (8.69)

ensure that V (·) is a Lyapunov f unction for the closed-loop system (8.64).

As discussed in [449], it is important to recognize that the function L

(x),

which appears in the integrand of the performance functional (8.57) is an

arbitrary function of x ∈ R

subject to conditions (8.60) and (8.62). Thus ,

(x) provides ﬂexibility in choosing the control law. This ﬂexibility will

be used in the following chapter to connect this inverse optimal control

framework to backstepping control methods [247].

As noted in [449], with L

(x) given by (8.66) and φ(x) given by (8.65),

L(x, u) can be expressed as

L(x, u) = u

(x)u − φ

(x)R

(x)φ(x) + L

(x)(u − φ(x))

−V

′

(x)[f(x) + G(x)φ(x)]



u +

−1

(x)L

(x)



(x)



u +

−1

(x)L

(x)



− V

′

(x)[f(x)

+G(x)φ(x)] −

′

(x)G(x)R

−1

(x)G

(x)V

′T

(x). (8.70)

Since R

(x) > 0, x ∈ R

, the ﬁrst term on the right-hand side of (8.70) is

nonnegative, while (8.69) implies that the second term is also nonnegative.

Thus , it follows that

L(x, u) ≥ −

′

(x)G(x)R

−1

(x)G

(x)V

′T

(x), (8.71)