Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 495

1/2

2,¯p

sup

t≥0

∞

ˆu

G(τ)G

(τ)ˆudτ

1/2

2,¯p

ˆu

Qˆu

= kQ

1/2

2,¯p

which further implies that |||G|||

(∞,p),(2,2)

= kQ

1/2

2,¯p

iv) Note that for all t ≥ 0,

ky(t)k

≤

∞

kG(t −τ )u(τ)k

dτ

≤

∞

kG(t −τ )k

p,r

ku(τ)k

dτ

≤ su p

t≥0

kG(t)k

p,r

∞

ku(τ)k

dτ

≤ su p

t≥0

kG(t)k

p,r

|||u|||

1,r

which implies that |||G|||

(∞,p),(1,r)

≤ sup

t≥0

kG(t)k

p,r

Next, let ε > 0 and t

∈ [0, ∞) be such that kG(t

p,r

> sup

t≥0

kG(t)k

p,r

− ε. In addition, let u

(·) = v

(·)ˆu, k = 1, 2, . . ., w here ˆu ∈ R

is such that kˆuk

= 1, kG(t

)ˆuk

= kG(t

p,r

kˆuk

, and measurable v

[0, ∞) → R is such that |||v

|||

1,1

= 1 and, as k → ∞, v

(·) → δ(·), where δ(·)

is the Dirac delta function. In this case, note that |||u

|||

1,r

= 1, k = 1, 2, . . .,

and y

(t) → G(t)ˆu, t ≥ 0, as k → ∞, where y

(t)

△

= (G ∗ u

)(t). Hence,

|||G|||

(∞,p),(1,r)

≥ lim

k→∞

sup

t≥0

(t)k

= sup

t≥0

kG(t)ˆuk

≥ kG(t

)ˆuk

= kG(t

p,r

> sup

t≥0

kG(t)k

p,r

− ε,

which implies that

sup

t≥0

kG(t)k

p,r

− ε < |||G|||

(∞,p),(1,r)

≤ sup

t≥0

kG(t)k

p,r

, ε > 0,

and h en ce, (7.76) holds.

v) Note that for all u ∈ L

and y ∈ L

∞

it follows that |||u|||

r,r

= k¯uk

and |||y|||

∞,∞

= k¯yk

∞

, where ¯u ∈ R

and ¯y ∈ R

with ¯u

= |||u

|||

r,r

, i =

1, . . . , m, and ¯y

= |||y

|||

∞,∞

, i = 1, . . . , l. Next, it follows from Lemma 7.6

NonlinearBook10pt November 20, 2007

496 CHAPTER 7

that |||G

(i,j)

|||

(∞,∞),(r,r)

= |||G

(i,j)

|||

¯r,¯r

, and hence,

|||y

|||

∞,∞

= |||

j=1

(i,j)

∗ u

|||

∞,∞

≤

j=1

|||G

(i,j)

∗u

|||

∞,∞

≤

j=1

|||G

(i,j)

|||

¯r,¯r

|||u

|||

r,r

≤ krow

[¯r,¯r]

¯r

k¯uk

≤ max

i=1,...,l

krow

[¯r,¯r]

¯r

k¯uk

which implies that |||y|||

∞,∞

= k¯yk

∞

≤ max

i=1,...,l

krow

[¯r,¯r]

¯r

|||u|||

r,r

, and

hence,

|||G|||

(∞,∞),(r,r)

≤ max

i=1,...,l

krow

[¯r,¯r]

¯r

. (7.79)

Next, let I ∈ {1, . . . , l} be such that krow

[¯r,¯r]

¯r

= max

i=1,...,l

krow

[¯r,¯r]

¯r

. Now, let ˆu ∈ R

be such that kˆuk

= 1, let row

[¯r,¯r]

)ˆu =

krow

[¯r,¯r]

¯r

, and let u

∈ L

, j = 1, . . . , m, be s uch that |||u

|||

r,r

= ˆu

and lim

t→∞

(I,j)

∗ u

)(t) = |||G

(I,j)

|||

¯r,¯r

|||u

|||

r,r

. Note that existence of such

a u

(·) follows from Lemma 7.6. Now,

|||y|||

∞,∞

≥ |||y

|||

∞,∞

≥ lim

t→∞

(t)|

= lim

t→∞

j=1

(I,j)

∗u

)(t)|

j=1

|||G

(I,j)

|||

¯r,¯r

|||u

|||

r,r

= row

[¯r,¯r]

)¯u

= krow

[¯r,¯r]

¯r

which, with (7.79), implies (7.77).

vi) For p = ∞, (7.78) is a direct consequence of iv) or v). Now,

let p ∈ [1, ∞) and note that it follows from Lemma 7.4 that |||y|||

p,p

sup

{ˆy∈L

¯p

: |||ˆy|||

¯p, ¯p

=1}

hy, ˆyi. Hence, with p = r = 1 it follows from Lemma

7.3 that

|||y|||

p,p

= sup

|||ˆy|||

¯p, ¯p

∞

(t)ˆy(t)dt

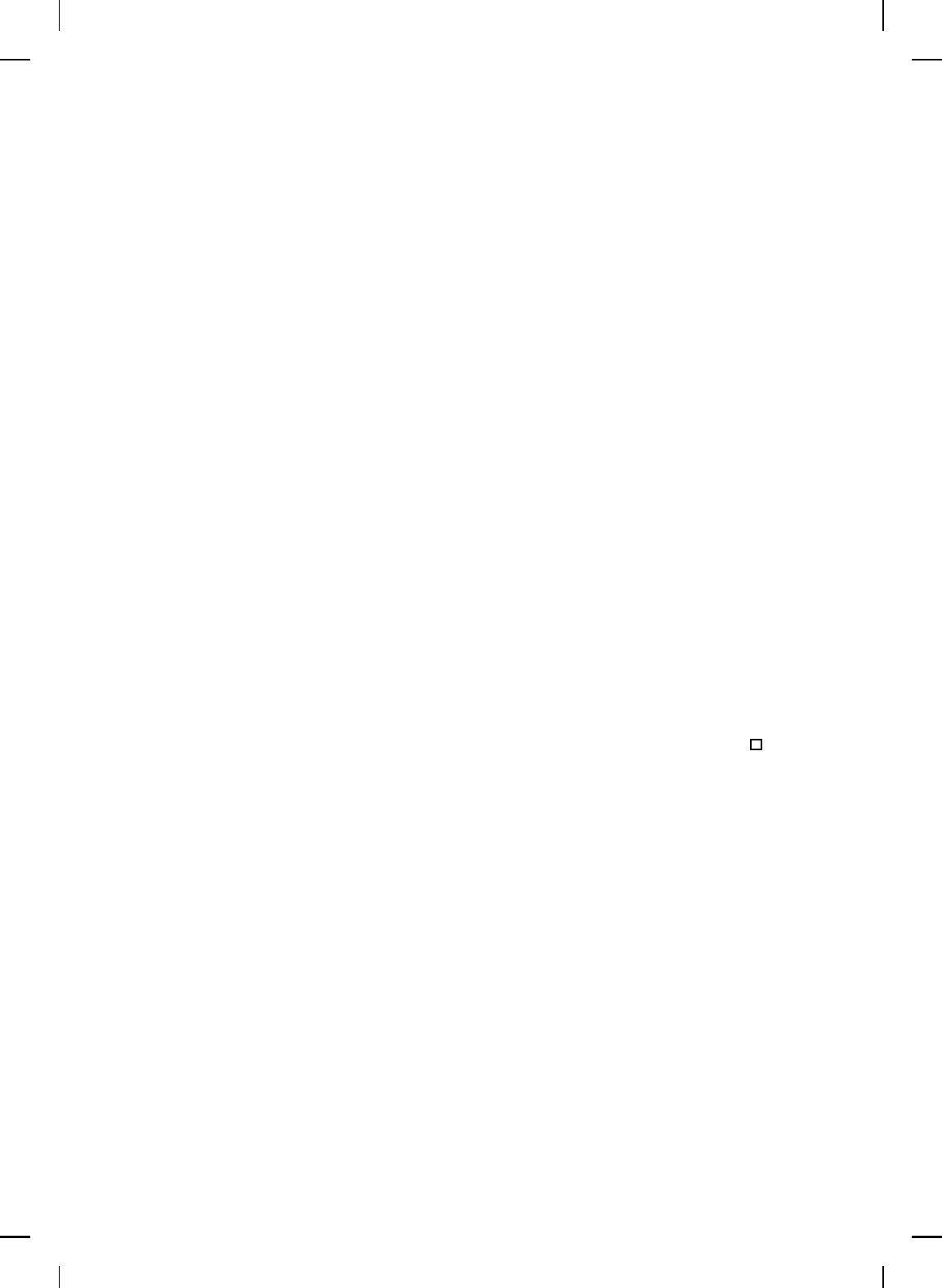
NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 497

= sup

|||ˆy|||

¯p, ¯p

∞



∞

(τ)G

(t − τ)dτ



ˆy(t)dt

= sup

|||ˆy|||

¯p, ¯p

∞

(τ)



∞

(t − τ)ˆy(t)dt



dτ

= sup

|||ˆy|||

¯p, ¯p

hu, ˆui

≤ |||u|||

1,1

sup

|||ˆy|||

¯p, ¯p

|||ˆu|||

∞,∞

where ˆu(t)

△

∞

(τ − t)ˆy(τ)dτ. Now, with r = ¯p, it follows from v) that

|||G|||

(p,p),(1,1)

≤ sup

|||ˆy|||

¯p, ¯p

|||ˆu|||

∞,∞

= max

j=1,...,m

kcol

[p,p]

. (7.80)

Next, let J ∈ {1, . . . , m} be such that kcol

[p,p]

= max

j=1,...,m

kcol

[p,p]

and let u

(·)

△

= v

(·)e

, k = 1, 2, . . ., where v

: [0, ∞) → R is

a measurable function su ch that |||v

|||

1,1

= 1 and, as k → ∞, v

(·) → δ(·),

where δ(·) is the Dirac delta function. In this case note that |||u

|||

1,1

= 1, k =

1, 2, . . ., and y

(t) → col

(G(t)), t ≥ 0, as k → ∞, where y

(t)

△

= (G ∗u

)(t).

Hence,

|||G|||

(p,p),(1,1)

≥ lim

k→∞

|||y

|||

p,p

= |||col

(G)|||

p,p

= kcol

[p,p]

= max

j=1,...,m

kcol

[p,p]

which, with (7.80), implies (7.78).

The following corollary specializes Theorem 7.7 to the results given

in [461, 462] and [104, p. 26].

Corollary 7.3. The following statements hold:

i) G : L

→ L

, |||G|||

(2,2),(1,2)

= σ

1/2

max

(P), and |||G|||

(2,2),(1,1)

= d

1/2

max

(P).

ii) G : L

→ L

∞

, |||G|||

(∞,2),(2,2)

= σ

1/2

max

(Q), and |||G|||

(∞,∞),(2,2)

= d

1/2

max

(Q).

iii) G : L

→ L

∞

, |||G|||

(∞,∞),(1,1)

= sup

t≥0

kG(t)k

∞

, and |||G|||

(∞,2),(1,2)

sup

t≥0

max

(G(t)).

iv) G : L

∞

→ L

∞

, and |||G|||

(∞,∞),(∞,∞)

= max

i=1,...,l

krow

[1,1]

v) G : L

→ L

, and |||G|||

(1,1),(1,1)

= max

j=1,...,m

kcol

[1,1]

NonlinearBook10pt November 20, 2007

498 CHAPTER 7

Recall th at the H

norm of the system (7.52) and (7.53) is given by

|||G|||

= kP

1/2

= kQ

1/2

. Hence, using the fact that k·k

= σ

max

(·) for

rank-one matrices, it follows from i) of Corollary 7.3 that if B (and hence

P) is a rank-one m atrix then |||G|||

= |||G|||

(2,2),(1,2)

. Similarly, it follows

from ii i) of Corollary 7.3 that if C (and hence Q) is a r ank -one matrix then

|||G|||

= |||G|||

(∞,2),(2,2)

. Hence, in th e single-input/multi-output and multi-

input/single-output cases th e H

norm of a dynamical system is induced. In

the multi-input/multi-output case, however, the H

norm does not appear

to be induced. For related details see [84].

Theorem 7.7 also applies to the more general case w here G is a

noncausal, time-invariant operator. In this case, the input-output spaces

and L

are deﬁ ned for t ∈ (−∞, ∞), H(ω) is the Fourier transform of

G(t), and the lower limit in the integrals deﬁning P and Q is replaced by

−∞.

An alternative characterization of input-output properties is the

Hankel norm which provides a mapping from past inputs u(t), t ∈ (−∞, 0],

to future outputs y(t), t ∈ [0, ∞) [136, 461]. For causal dynamical systems

the Hankel operator Γ : L

(−∞, 0] → L

is deﬁn ed by

y(t) = (Γ ∗ u)(t)

△

∞

G(t + τ)u(−τ )dτ, t ∈ [0, ∞), (7.81)

where L

(−∞, 0] d en otes the set of functions in L

on the time interval

(−∞, 0], and the induced Hankel norm |||Γ|||

(q,s),(p,r)

is deﬁn ed by

|||Γ|||

(q,s),(p,r)

△

= sup

|||u|||

p,r

|||Γ ∗ u|||

q,s

. (7.82)

Proposition 7.3. The following statements hold:

i) Γ : L

(−∞, 0] → L

, and

|||Γ|||

(2,2),(2,2)

= λ

1/2

max

(P Q). (7.83)

ii) Let r ∈ [1, ∞]. Then Γ : L

(−∞, 0] → L

, and

|||Γ|||

(2,2),(1,r)

= kP

1/2

2,r

. (7.84)

iii) Let p ∈ [1, ∞]. Then Γ : L

(−∞, 0] → L

∞

, and

|||Γ|||

(∞,p),(2,2)

= kQ

1/2

2,¯p

. (7.85)

iv) Let p, r ∈ [1, ∞]. T hen Γ : L

(−∞, 0] → L

∞

, and

|||Γ|||

(∞,p),(1,r)

= sup

t≥0

kG(t)k

p,r

. (7.86)

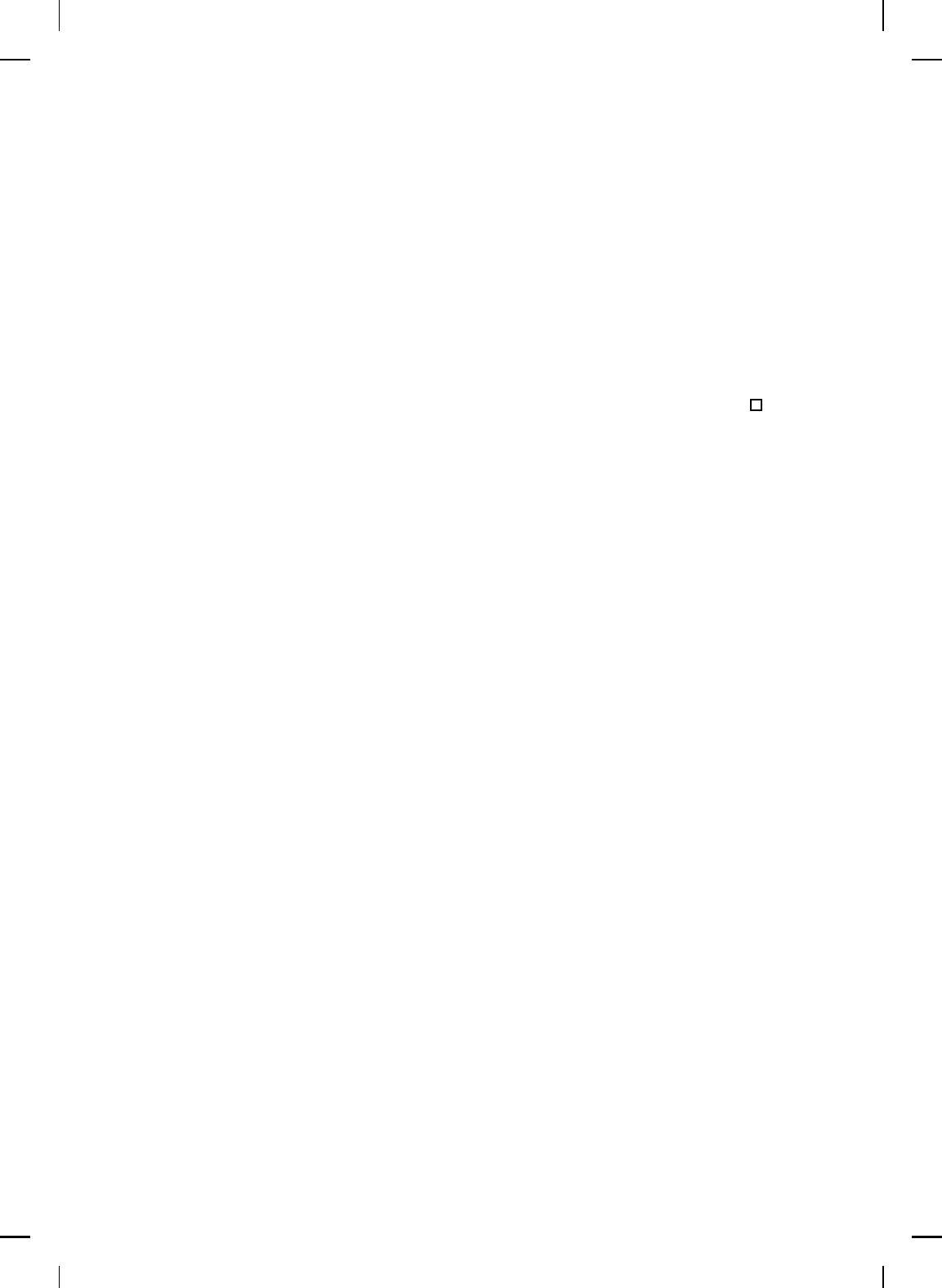
NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 499

v) Let r ∈ [1, ∞]. Then Γ : L

(−∞, 0] → L

∞

, and

|||Γ|||

(∞,∞),(r,r)

= max

i=1,...,l

krow

[¯r,¯r]

¯r

. (7.87)

vi) Let p ∈ [1, ∞]. Then Γ : L

(−∞, 0] → L

, and

|||Γ|||

(p,p),(1,1)

= max

j=1,...,m

kcol

[p,p]

. (7.88)

Proof. The proof of i) is standard; see [136] for a proof. The proof

of ii)–vi) is similar to that of ii)–vi) of Theorem 7.7 with appropriate

modiﬁcations to the time interval for the input space.

7.9 Finitely Computable Upper Bounds for |||G|||

(∞,p),(1,r)

In this section, we obtain a ﬁn itely computable upper bound for (7.76). To

do this we assume that there exist H

(s), H

(s) ∈ RH

such that H(s) =

(s)H

(s), where H(s) ∈ RH

denotes the Laplace transform of G(t).

Note that such a factorization exists only if H(s) has relative degree two.

Furth ermore, note that the above factorization exists if and only if there

exist linear, time-invariant asymptotically stable dynamical systems with

impulse response functions G

: R → R

l×m

and G

: R → R

×m

such

that G

(t) = 0 and G

(t) = 0, t < 0, and

G(t) =

∞

(t − τ)G

(τ)dτ, t ≥ 0. (7.89)

Next, let G

: L

→ L

∞

and G

: L

→ L

denote the convolution operators

of G

and G

, respectively, and deﬁne P

∈ R

m×m

and Q

∈ R

l×l

△

∞

(t)G

(t)dt, Q

△

∞

(t)G

(t)dt. (7.90)

Finally, let G

(t) = C

, t ≥ 0, and G

(t) = C

, t ≥ 0,

where A

∈ R

×n

, B

∈ R

×m

, C

∈ R

l×n

, A

∈ R

×n

, B

∈ R

×m

and C

∈ R

×n

, and let P

∈ R

×n

and Q

∈ R

×n

be the unique,

nonnegative-deﬁnite solutions to the Lyapu nov equations

0 = A

+ P

+ C

, 0 = A

+ Q

+ B

. (7.91)

Note that P

= B

and Q

= C

Proposition 7.4. Let p, r ∈ [1, ∞]. If there exist G

: R → R

l×m

and

: R → R

×m

such that (7.89) holds, then

|||G|||

(∞,p),(1,r)

≤ kQ

1/2

2,¯p

1/2

2,r

. (7.92)

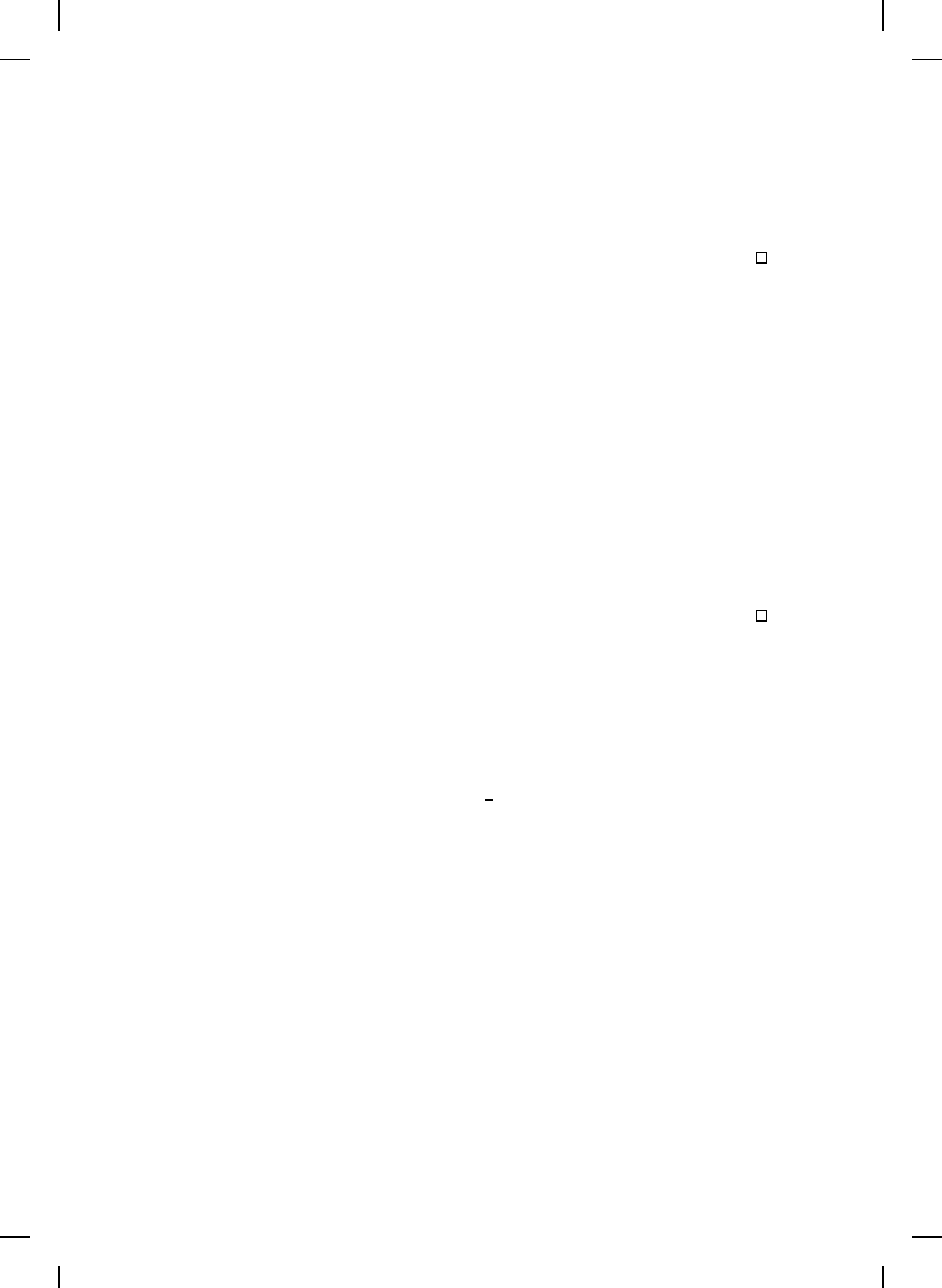
NonlinearBook10pt November 20, 2007

500 CHAPTER 7

Proof. Note that y(t) = (G

∗(G

∗u))(t). Now, since G

: L

→ L

∞

and G

: L

→ L

it follows fr om Theorem 7.7 th at

|||y|||

∞,p

≤ kQ

1/2

2,¯p

|||G

∗ u|||

2,2

≤ kQ

1/2

2,¯p

1/2

2,r

|||u|||

1,r

which implies (7.92).

The following corollary of Proposition 7.4 provides ﬁnitely computable

bounds for the mixed-induced signal norm (7.76).

Corollary 7.4. Let P

and Q

be given by (7.90). Then the following

inequalities h old:

i) |||G|||

(∞,∞),(1,1)

≤ d

1/2

max

1/2

max

ii) |||G|||

(∞,2),(1,2)

≤ σ

1/2

max

)σ

1/2

max

iii) |||G|||

(∞,∞),(1,2)

≤ d

1/2

max

)σ

1/2

max

iv) |||G|||

(∞,2),(1,1)

≤ σ

1/2

max

1/2

max

Proof. The resu lts follow from Theorem 7.7 and Proposition 7.4.

7.10 Upper Bounds for L

Operator Norms

In this section, we provide upper bounds for the L

operator norm

|||G|||

(∞,p),(∞,r)

. For α > 0, deﬁne the shifted impulse response function

: R → R

l×m

(t)

△



0 t < 0,

(A+

I)t

B, t ≥ 0,

(7.93)

and let G

denote its convolution operator

y(t) = (G

∗u)(t)

△

∞

(t −τ)u(τ)dτ. (7.94)

Furth ermore, for some of the results in this section we assume there

exist H

(s), H

(s) ∈ RH

such that H

(s) = H

(s)H

(s), where

(s) ∈ RH

denotes the Laplace transform of G

(t). Note that the

above factorization exists if and only if there exist linear time-invariant

asymptotically stable dynamical systems with impulse response functions

: R → R

l×m

and G

: R → R

×m

such that G

(t) = 0 and

(t) = 0, t < 0, and

(t) =

∞

(t − τ)G

(τ)dτ, t ≥ 0. (7.95)

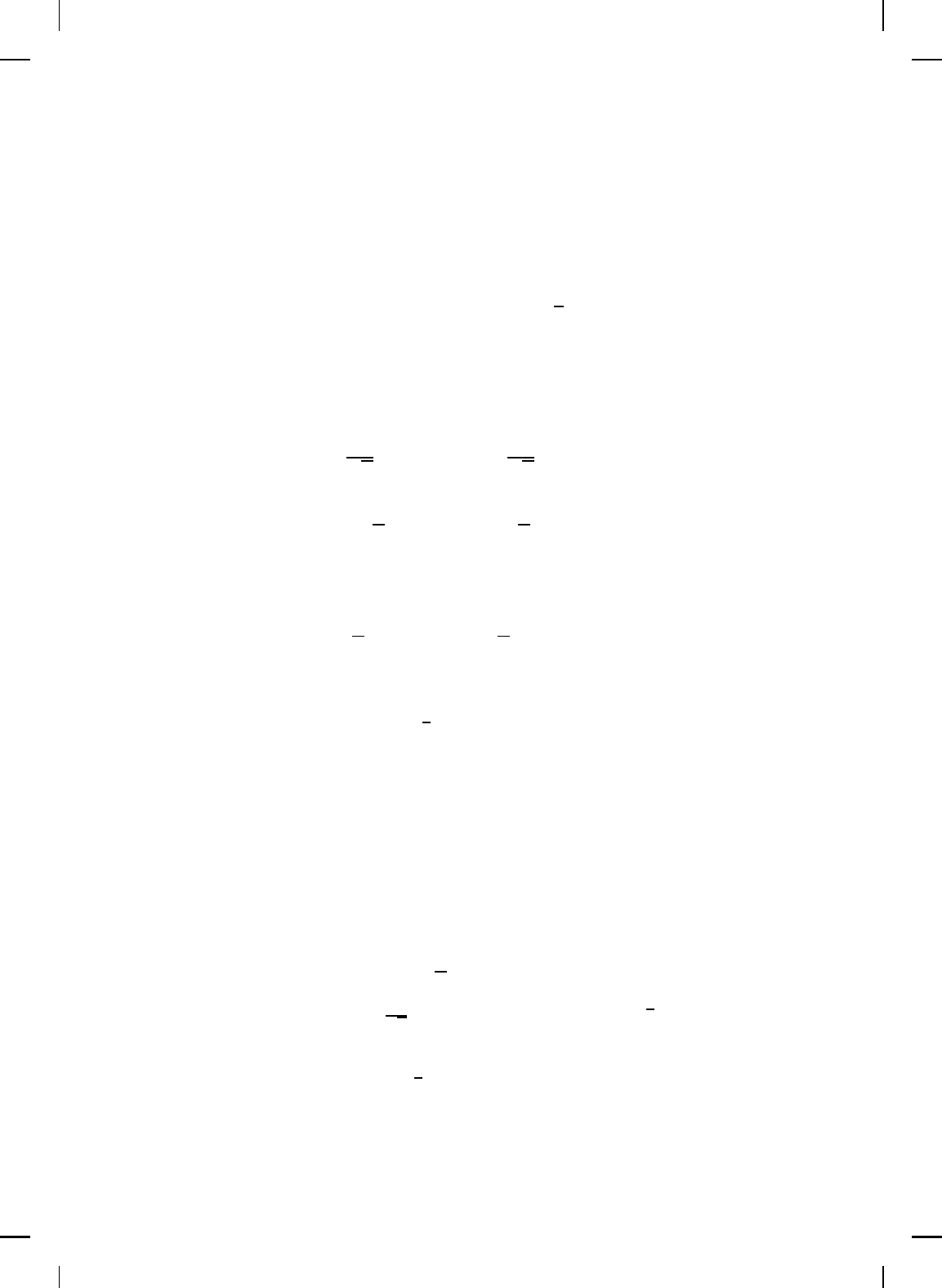
NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 501

Next, let G

: L

→ L

∞

and G

: L

→ L

denote the convolution

operators of G

and G

, respectively, and deﬁn e P

∈ R

m×m

and Q

∈

l×l

△

∞

(t)G

(t)dt, Q

△

∞

(t)G

(t)dt. (7.96)

Theorem 7.8. Let α > 0 be such that A +

I is asymptotically stable

and let Q

∈ R

n×n

be the unique, nonnegative-deﬁnite solution to the

Lyapunov equ ation

0 = AQ

+ Q

+ αQ

+ BB

. (7.97)

Furth ermore, let p, r ∈ [1, ∞]. Then G : L

∞

→ L

∞

|||G|||

(∞,p),(∞,2)

≤

√

|||G

|||

(∞,p),(2,2)

√

k(CQ

)

1/2

2,¯p

, (7.98)

and

|||G|||

(∞,p),(∞,r)

≤

|||G

|||

(∞,p),(1,r)

sup

t≥0

(t)k

p,r

. (7.99)

In addition, if there exist G

: R → R

l×m

and G

: R → R

×m

such

that (7.95) holds, then

|||G|||

(∞,p),(∞,r)

≤

|||G

|||

(∞,p),(1,r)

≤

1/2

2,¯p

1/2

2,r

. (7.100)

Proof. Let T > 0, u ∈ L

∞

, and deﬁne

(t)

△



(t−T )

u(t), 0 ≤ t ≤ T,

0, t > T.

(7.101)

Now, note that

|||u

|||

2,2

∞

(t)k

α(t−T )

ku(t)k

≤ |||u|||

∞,2

α(t−T )

|||u|||

∞,2

or, equivalently, |||u

|||

2,2

≤

√

|||u|||

∞,2

. Next, deﬁne y

(t)

△

= e

(t−T )

y(t) and,

since G(t) = 0, t < 0, note that

(t) =

∞

(t−T )

G(t − τ)u(τ)dτ

NonlinearBook10pt November 20, 2007

502 CHAPTER 7

∞

(t−τ)

G(t − τ)e

(τ−T )

u(τ)dτ

∞

(t − τ)u

(τ)dτ

= (G

∗ u

)(t).

Next, it follows from (7.75) that

(t)k

≤ |||G

|||

(∞,p),(2,2)

|||u

|||

2,2

≤

√

|||G

|||

(∞,p),(2,2)

|||u|||

∞,2

Now, noting that y(T ) = y

(T ) it follows that

ky(T )k

≤

√

|||G

|||

(∞,p),(2,2)

|||u|||

∞,2

, T ≥ 0,

which implies (7.98).

Let T > 0, u ∈ L

∞

, and let u

(·) be given by (7.101). Then

|||u

|||

1,r

∞

(t)k

(t−T )

ku(t)k

≤ |||u|||

∞,r

(t−T )

|||u|||

∞,r

Now, it follows from (7.76) that

(t)k

≤ |||G

|||

(∞,p),(1,r)

|||u

|||

1,r

≤

|||G

|||

(∞,p),(1,r)

|||u|||

∞,r

Hence, since y(T ) = y

(T ),

ky(T )k

≤

|||G

|||

(∞,p),(1,r)

|||u|||

∞,r

, T ≥ 0,

which implies (7.99). Finally, (7.100) follows from (7.99) and Proposition

7.4.

Next we specialize Theorem 7.8 to Euclidean and inﬁnity norms.

Corollary 7.5. Let α > 0 be such that A+

I is asymptotically stable,

let G

(·) be given by (7.93), and let Q

∈ R

n×n

be th e un ique, non negative-

deﬁnite solution to (7.97). Then the following statements hold:

NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 503

|||G|||

(∞,2),(∞,2)

≤

√

|||G

|||

(∞,2),(2,2)

√

1/2

max

(CQ

). (7.102)

Furth ermore, if there exist G

: R → R

l×m

and G

: R → R

×m

such that (7.95) holds, then

|||G|||

(∞,2),(∞,2)

≤

|||G

|||

(∞,2),(1,2)

≤

1/2

max

)σ

1/2

max

(7.103)

ii)

|||G|||

(∞,∞),(∞,2)

≤

√

|||G

|||

(∞,∞),(2,2)

√

1/2

max

(CQ

(7.104)

Furth ermore, if there exist G

: R → R

l×m

and G

: R → R

×m

such that (7.95) holds, then

|||G|||

(∞,∞),(∞,2)

≤

|||G

|||

(∞,∞),(1,2)

≤

1/2

max

)σ

1/2

max

(7.105)

Proof. The proof is a direct consequence of Lemma 7.1 and Theorem

7.8.

Using set theoretic arguments involving closed convex sets and support

functions, the L

norm bound in (7.102) was given by Schweppe [393].

Within the context of L

∞

equi-induced norms, this L

norm bound is

referred to as the star-norm in [324, 423]. The expression given by (7.103)

provides an alternative ﬁnitely computable bound for th e L

∞

equi-induced

norm.

A s ummary of the resu lts of Sections 7.8–7.10 is given in Table 7.1.

Next, we present an example to provide comparisons between the

bounds (7.98)–(7.100) given in Theorem 7.8 for |||G|||

(∞,p),(∞,r)

, p, r ∈ [1, ∞].

Example 7.4. Consider the system (7.52) and (7.53) with

A =



−1 0

1 −1



, B =





, C =



0 1



so that G(t) = te

−t

, t ≥ 0. Since G is a convolution operator for a single-

input/single-output sys tem it follows that |||G|||

(∞,∞),(∞,∞)

= |||G|||

(∞,p),(∞,r)

NonlinearBook10pt November 20, 2007

504 CHAPTER 7

Table 7.1 Summary of induced operator norms for p, r ∈ [1, ∞].

Input Output Induced Norm Upper Bound

||| · |||

2,2

||| · |||

2,2

sup

ω ∈R

max

(H(ω))

||| · |||

1,r

||| · |||

2,2

1/2

2,r

||| · |||

2,2

||| · |||

∞,p

1/2

2,¯p

||| · |||

1,r

||| · |||

∞,p

sup

t≥0

kG(t)k

p,r

1/2

2,¯p

1/2

2,r

||| · |||

r,r

||| · |||

∞,∞

max

i=1,...,l

krow

[¯r,¯r]

¯r

||| · |||

1,1

||| · |||

p,p

max

j=1,...,m

kcol

[p,p]

||| · |||

∞,2

||| · |||

∞,p

√

kCQ

2,¯p

||| · |||

∞,r

||| · |||

∞,p

sup

t≥0

(t)k

p,r

||| · |||

∞,r

||| · |||

∞,p

1/2

2,¯p

1/2

2,r

p, r ∈ [1, ∞]. Hence, it follows from Lemma 7.6 with r = ∞ that

|||G|||

(∞,∞),(∞,∞)

∞

|G(t)|dt =

∞

−t

dt = 1.

Now, with p = 2, it follows from (7.98) that

|||G|||

(∞,∞),(∞,∞)

≤

√

|||G

|||

(∞,2),(2,2)

for all 0 < α < 2. Noting th at

|||G

|||

(∞,2),(2,2)

∞

(t)dt =

∞

−(2−α)t

dt =

(2 − α)

it follows that

|||G|||

(∞,∞),(∞,∞)

≤ inf

0<α<2

α(2 − α)

≈ 1.0887.

Next, using (7.99) to bound |||G|||

(∞,∞),(∞,∞)

yields

|||G|||

(∞,∞),(∞,∞)

≤

sup

t≥0

(t) =

α(2 − α)

−1

, 0 < α < 2,

which implies

|||G|||

(∞,∞),(∞,∞)

≤ inf

0<α<2

α(2 −α)

−1

= 4e

−1

≈ 1.4715.

Finally, we compare (7.100) to (7.98) and (7.99). Since H

(s) =

(s+1−

)