Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 475

where x(t), u(t), and y(t) ∈ R. Now, it f ollows that

y(t) = x(t) =

t−τ

u(τ)dτ,

which implies that for all u(·) ∈ L

, y(·) ∈ L

. Next, let u(t) = e

−t

so that

u(·) ∈ L

. In this case,

y(t) =

t−τ

−τ

dτ = sinh t,

which implies that y(·) 6∈ L

. Hence, G given by (7.11) and (7.12) is n ot

-stable. Note that the zero solution to (7.11) is unstable. △

Example 7.2. In this example, let G

: L

∞e

→ L

∞e

, i = 1, 2, 3, be

given by

[u](t) = u

(t),

[u](t) = u(t) + 1,

[u](t) = log

(1 + u

(t)).

It is clear that G

is L

∞

-stable. However, note that there does not exist

constants γ and β (with p = ∞) such that (7.7) holds which implies that

is not L

∞

-stable with ﬁnite gain. Next, since |||G

[u]|||

∞

≤ |||u|||

∞

+ 1 it

follows that G

is L

∞

-stable with ﬁnite gain but not L

∞

-stable with ﬁnite

gain and zero bias. Finally, since |||G

[u]|||

∞

≤

√

2|||u|||

∞

it follows that G

∞

-stable with ﬁn ite gain and zero bias. △

Example 7.3. Consider the scalar operator dynamical system G given

by the mapping

y(t) = G[u](t) =

α(t−τ)

u(τ)dτ, t ≥ 0,

where α ∈ R. Let u(·) ∈ L

∞e

, let T > 0, and note that f or all t ≤ T ,

|y(t)| ≤

α(t−τ)

|u(τ)|dτ

≤ |||u

|||

∞

α(t−τ)

dτ

αt

−1

|||u

|||

∞

≤

|α|T

− 1

|α|

|||u

|||

∞

which implies that |||y

|||

∞

≤

|α|T

−1

|α|

|||u

|||

∞

, establishing that G : L

∞e

→

∞e

NonlinearBook10pt November 20, 2007

476 CHAPTER 7

Now, let α < 0 and let u(·) ∈ L

∞

. In this case, it follows that for all

t > 0,

|y(t)| ≤ |||u|||

∞

α(t−τ)

dτ

αt

− 1

|||u|||

∞

≤

|α|

|||u|||

∞

which implies that G is L

∞

-stable with ﬁnite gain and zero bias for all α < 0.

Finally, let α > 0 and let u(t) ≡ 1 so that u(·) ∈ L

∞

. In this case,

y(t) =

αt

−1

, which implies that y(·) 6∈ L

∞

. Hence, G is not L

∞

-stable f or

all α > 0. △

7.3 The Small Gain Theorem

In this section, we consider feedback interconnections of input-output

stable systems and provide suﬃcient conditions for inpu t-output stability of

interconnected systems. Speciﬁcally, let G

: L

→ L

and G

: L

→ L

and consider the negative feedback interconnection given in Figure 7.1 where

, u

) ∈ L

× L

and (y

, y

) ∈ L

× L

are the in put and the output

signals of the closed-loop system, respectively, and e

△

= u

− y

∈ L

and

△

= u

+ y

∈ L

are the inp uts to G

and G

, respectively. Note that

= G

] = G

− y

] and y

= G

] = G

+ y

]. Hence,







− y

]

+ y

]



(7.13)

and







+ G

]

− G

]



. (7.14)

In general, there may not exist a mapping

G : L

× L

→ L

× L

such that y =

G[u], where y

△

= [y

, y

]

and u

△

= [u

, u

]

, and (7.13) holds.

In this chapter, we restrict G

and G

such that there exists a mapping

G : L

×L

→ L

×L

such that y =

G[u] and (7.13) holds. In this case,

the feedb ack interconnection given in Figure 7.1 is well deﬁned. Note that

such a

G exists if and only if there exists a mapping

G : L

×L

→ L

×L

such that e =

G[u], where e

△

= [e

, e

]

, and (7.14) holds.

Deﬁnition 7.4. Let the feedback interconnection of G

and G

given

in Figure 7.1 be well deﬁned and let

G : L

×L

→ L

×L

be such that

NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 477



- - -

 

−

Figure 7.1 Feedback interconnection of G

and G

y =

G[u] and (7.13) holds. Then the feedback interconnection of G

and

given in Figure 7.1 is, respectively, L

-stable, L

-stable with ﬁnite gain,

and L

-stable with ﬁnite gain and zero bias if

G is L

-stable, L

-stable with

ﬁnite gain, and L

-stable with ﬁnite gain and zero bias.

The following result, known as small gain theorem provides a suﬃcient

condition for L

-stability of the feedback interconnection given by Figure 7.1.

Theorem 7.1. Let G

: L

→ L

and G

: L

→ L

be causal

operator dynamical systems such that the feedback interconnection given

by Figure 7.1 is well deﬁned. If G

is L

-stable with ﬁnite gain γ

and

is L

-stable with ﬁnite gain γ

such that γ

< 1, then the feedback

interconnection of G

and G

given in Figure 7.1 is L

-stable.

Proof. Since G

and G

are causal and L

-stable with ﬁnite gains γ

and γ

, respectively, it follows that there exist β

, β

> 0 su ch that for every

T > 0, e

∈ L

, and e

∈ L

|||(G

])

|||

≤ γ

|||e

|||

+ β

, (7.15)

|||(G

])

|||

≤ γ

|||e

|||

+ β

. (7.16)

Hence, it follows that

|||e

|||

≤ |||u

|||

+ |||(G

])

|||

≤ |||u

|||

+ γ

|||e

|||

+ β

, (7.17)

and

|||e

|||

≤ |||u

|||

+ |||(G

])

|||

≤ |||u

|||

+ γ

|||e

|||

+ β

. (7.18)

NonlinearBook10pt November 20, 2007

478 CHAPTER 7

Now, combining (7.17) and (7.18) yields

|||e

|||

≤ |||u

|||

+ β

+ γ

(|||u

|||

+ γ

|||e

|||

+ β

) , (7.19)

|||e

|||

≤ |||u

|||

+ β

+ γ

(|||u

|||

+ γ

|||e

|||

+ β

) , (7.20)

and h en ce,

|||e

|||

≤

1 −γ

(|||u

|||

+ γ

|||u

|||

+ β

+ γ

) , (7.21)

|||e

|||

≤

1 −γ

(|||u

|||

+ γ

|||u

|||

+ β

+ γ

) . (7.22)

Next, since y

= G

] and y

= G

] it follows f rom (7.15), (7.16), (7.21),

and (7.22) that

|||y

|||

≤

1 −γ

(|||u

|||

+ γ

|||u

|||

+ β

+ γ

) + β

, (7.23)

|||y

|||

≤

1 −γ

(|||u

|||

+ γ

|||u

|||

+ β

+ γ

) + β

. (7.24)

Now, the result follows from the fact that G

and G

are causal dynamical

systems.

7.4 Input-Output Dissipativity Theory

In this s ection, we introduce the concept of dissipative systems within the

context of operator d ynamical systems. In order to do this, we restrict our

attention to operator dynamical systems that map L

to L

. Note that

-space is a Hilbert space (see Problem 2.89) with the inner product

hu, yi

△

∞

(t)y(t)dt, u(·), y(·) ∈ L

. (7.25)

For u, y ∈ L

deﬁne hu, yi

△

= hu

, y

i. The following deﬁnition introduces

the notion of dissipativity for operator dynamical systems.

Deﬁnition 7. 5. Let G : L

→ L

be a causal operator dynamical

system and let Q ∈ S

, R ∈ S

, and S ∈ R

l×m

. G is (Q, R, S)- dissipative if

for every T > 0 and for every u ∈ L

hy, Qyi

+ 2hy, Sui

+ hu, Rui

≥ 0, (7.26)

where y = G[u]. G is passive if f or every T > 0 and for every u ∈ L

2hy, ui

≥ 0. G is input strict passive if there exists ε > 0 such that for

every T > 0 and for every u ∈ L

, 2hy, ui

− εhu, ui

≥ 0. G is output

strict passive if there exists ε > 0 such that for every T > 0 and for every

u ∈ L

, 2hy, ui

− εhy, yi

≥ 0. G is input-output strict passive if there

exist ε

, ε

> 0 such that for every T > 0 and for every u ∈ L

, 2hy, ui

−

NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 479

hy, yi − ε

hu, ui

≥ 0. Finally, G is nonexpansive with gain γ > 0 if for

every T > 0 and f or every u ∈ L

, hy, yi

− γ

hu, ui

≤ 0.

The following result connects (Q, R, S)-dissipativity with L

-stability.

Theorem 7.2. Let G : L

→ L

be a causal operator dynamical

system and let Q ∈ S

, R ∈ S

, and S ∈ R

l×m

be such that Q < 0. If G is

(Q, R, S)-dissipative, then G is L

-stable.

Proof. Let M

△

= −Q and let λ > 0 be such that λI

+ R > 0 and

M −

≥ εI

for some ε > 0. (The existence of such a scalar λ can be

easily established.) Since G is (Q, R, S)-dissipative it follows that for every

T > 0 and u ∈ L

hy, Myi

≤ 2hy, Sui

+ hu, Rui

y, S

+ λhu, ui

− h

√

y −

√

λu,

√

y −

√

λui

+hu, Rui

≤

y, S

+ hu, (R + λI

)ui

, (7.27)

which implies that

εhy, yi

≤ hy, (M −

)yi

≤ hu, (R + λI

)ui

≤ (λ + λ

max

(R))hu, ui

. (7.28)

The result now follows immediately by noting that hy, yi

= |||y

|||

Corollary 7.1. Let G : L

→ L

be a causal operator dynamical

system. Then the following statements hold:

i) I f G is output strict passive, then G is L

-stable.

ii) If G is input-output strict passive, then G is L

-stable.

iii) If G is nonexpansive with gain γ > 0, then G is L

-stable.

Proof. The proof is a direct consequence of Theorem 7.2 with i)

Q = −εI

, R = 0, and S = I

, ii) Q = −ε

, R = −ε

, and S = I

, and

iii) Q = I

, R = − γ

, and S = 0.

Next, we provide a suﬃcient condition for input-output stability of a

feedback interconnection of two dissipative dynamical systems G

and G

NonlinearBook10pt November 20, 2007

480 CHAPTER 7

Theorem 7.3. Let G

: L

→ L

and G

: L

→ L

be causal

operator dynamical systems such that the feedback interconnection given

by Figure 7.1 is well deﬁned. Furthermore, let Q

, R

∈ S

, Q

, R

∈ S

and S

, S

∈ R

l×m

be such that there exists a scalar σ > 0 such that

△



+ σR

−S

+ σS

−S

+ σS

+ σQ



< 0.

If G

is (Q

, R

, S

)-dissipative and G

is (Q

, R

, S

)-dissipative, then the

feedback interconnection of G

and G

given in Figure 7.1 is L

-stable.

Proof. Since G

is (Q

, R

, S

)-dissipative and G

is (Q

, R

, S

dissipative it follows that for every T > 0, e

∈ L

, and e

∈ L

, Q

+ 2hy

, S

+ he

, R

≥ 0 (7.29)

and

σhy

, Q

+ 2σhy

, S

+ σhe

, R

≥ 0. (7.30)

Now, using e

= u

−y

and e

= u

+ y

, and combining (7.29) and (7.30)

yields

hy,

Qyi

+ 2hy,

Sui

+ hu,

Rui

≥ 0, (7.31)

where u

△

= [u

, u

]

, y

△

= [y

, y

]

, and

△



0 σR



△



−σR

−R

σS



The result now is an immediate consequence of Theorem 7.2.

Corollary 7.2. Let G

: L

→ L

and G

: L

→ L

be causal

operator dynamical systems such that the feedback interconnection given

by Figure 7.1 is well deﬁned. Then the following statements hold:

i) I f G

is input-output str ict passive and G

is passive, then th e feedback

interconnection of G

and G

given in Figure 7.1 is L

-stable.

ii) If G

and G

are input strict passive, then feedback interconnection of

and G

given in Figure 7.1 is L

-stable.

iii) If G

and G

are output strict passive, then the f eedback interconnec-

tion of G

and G

given in Figure 7.1 is L

-stable.

iv) If G

is input strict passive and L

-stable with ﬁnite gain and G

passive, then the feedback interconnection of G

and G

given in Figure

7.1 is L

-stable.

v) If G

is nonexp an s ive with gain γ

and G

is nonexp an s ive with gain

such that γ

< 1, then the feedback interconnection of G

and G

given in Figure 7.1 is L

-stable.

NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 481

Proof. i) The proof follows from Theorem 7.3 with l = m, σ = 1,

= −ε

, R

= −ε

, S

= I

, Q

= 0, R

= 0, and S

= I

for some

, ε

> 0.

ii) The proof follows from Theorem 7.3 with l = m, σ = 1, Q

= 0,

= −ε

, S

= I

, Q

= 0, R

= −ε

, and S

= I

for some

, ε

> 0.

iii) The proof follows from Theorem 7.3 with l = m, σ = 1, Q

−ε

, R

= 0, S

= I

, Q

= −ε

, R

= 0, and S

= I

for some

, ε

> 0.

iv) Note that if G

is input strict p assive and L

-stable with ﬁ nite

gain, then there exist s calars ε > 0 and γ > 0 such that for every T > 0 and

∈ L

2hy

, e

− εhe

, e

≥ 0 (7.32)

and

−hy

, y

+ γhe

, e

≥ 0. (7.33)

Now, let σ > 0 be such that σγ < ε. Addin g (7.32) to σ(7.33) yields

−σhy

, y

+ 2hy

, e

− (ε − σγ)he

, e

≥ 0,

which shows that G

is in put-output strict passive. The result now follows

from i).

v) Since γ

< 1 there exists ε > 0 such that (γ

+ ε)γ

< 1. The

result now follows from Theorem 7.3 with σ = γ

+ ε, Q

= −I

, R

= γ

= 0, Q

= −I

, R

= γ

, and S

= 0.

7.5 Input-Output Operator Dissipativity Theory

In this section, we extend the concept of dissipative systems introdu ced in

Section 7.4. Once again, we restrict our attention to operator dynamical

systems that map L

to L

. The following deﬁnition introduces the notion

of operator dissipativity for operator dynamical systems.

Deﬁnition 7. 6. Let G : L

→ L

be a causal operator dynamical

system and let Q : L

→ L

, R : L

→ L

, and S : L

→ L

causal operators such that Q and R are self-adjoint.

G is (Q, R, S)-operator

dissipative if for every T > 0 and for every u ∈ L

hy, Qyi

+ 2hy, Sui

+ hu, Rui

≥ 0, (7.34)

Given an operator X : L

→ L

, the operator X

∗

: L

→ L

is the adjoint operator of X

if for every u ∈ L

and y ∈ L

, hy, Xui = hX

∗

y , ui. An operator X : L

→ L

is self-adjoint

if for every u ∈ L

and y ∈ L

, hy, Xui = hXy, ui, that is, if X = X

∗

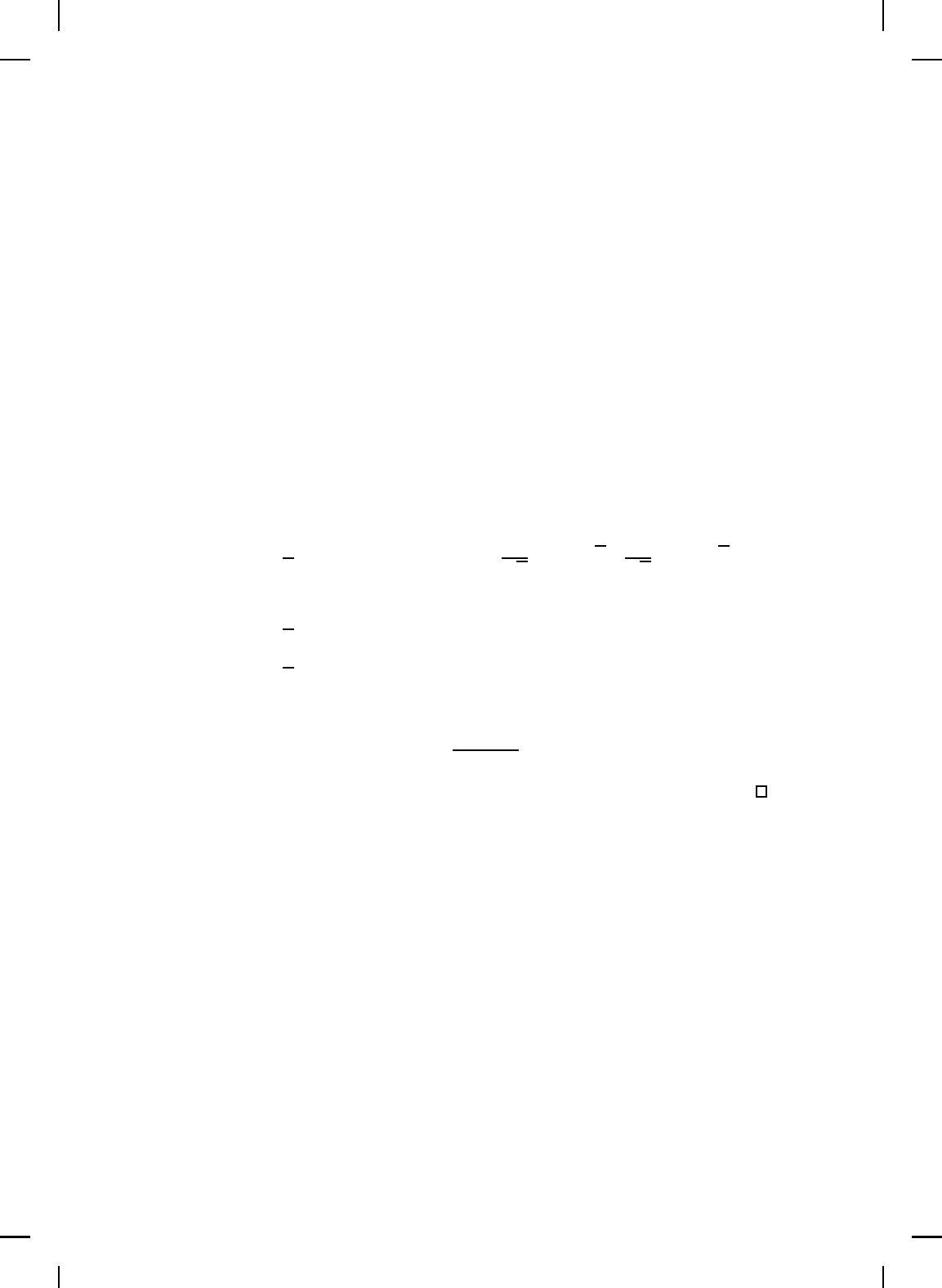
NonlinearBook10pt November 20, 2007

482 CHAPTER 7

where y = G[u].

The following result connects (Q, R, S)-operator dissipativity with L

stability.

Theorem 7.4. Let G : L

→ L

be a causal operator dynamical

system and let Q : L

→ L

, R : L

→ L

, and S : L

→ L

be causal

operators such that Q, R, and SS

∗

are bounded, that is, there exist positive

scalars q, r, and s such that hy, Qyi ≤ qhy, yi, y ∈ L

, hu, Rui ≤ rhu, ui,

u ∈ L

, hy, SS

∗

yi = hS

∗

y, S

∗

yi ≤ shy, yi, y ∈ L

, Q and R are self-adjoint,

and there exists ε > 0 such that hy, Qyi < −εhy, yi. If G is (Q, R, S)-op erator

dissipative, then G is L

-stable.

Proof. Let M

△

= −Q and let λ > 0 be such that λ < s/ε. Since G is

(Q, R, S)-operator dissipative it follows th at for every T > 0 and u ∈ L

εhy, yi

≤ hy, Myi

≤ 2hy, Sui

+ hu, Rui

∗

y, S

∗

+ λhu, ui

− h

√

∗

y −

√

λu,

√

∗

y −

√

λui

+hu, Rui

≤

∗

y, S

∗

+ (r + λ)hu, ui

≤

hy, yi

+ (r + λ)hu, ui

, (7.35)

which implies that

hy, yi

≤

λ(λ + r)

ελ − s

hu, ui

. (7.36)

The result now follows immediately by noting that hy, yi

= |||y

|||

Next, we provide a suﬃcient condition for input-output stability of a

feedback interconnection of two operator dissipative dynamical systems G

and G

Theorem 7.5. Let G

: L

→ L

and G

: L

→ L

be causal

operator dynamical systems such that the feedback interconnection given

by Figure 7.1 is well deﬁned. Furthermore, let Q

, R

: L

→ L

, Q

, R

→ L

, and S

, S

∗

: L

→ L

be bounded causal operators such that

there exist scalar σ, ε > 0 and

△



+ σR

−S

+ σS

∗

−S

∗

+ σS

+ σQ



satisﬁes hy,

Qyi ≤ −εhy, yi, y ∈ L

l+m

. If G

is (Q

, R

, S

)-operator

NonlinearBook10pt November 20, 2007

INPUT-OUTPUT STABILITY AND DISSIPATIVITY 483

dissipative and G

is (Q

, R

, S

)-operator dissipative, then feedback inter-

connection of G

and G

given in Figure 7.1 is L

-stable.

Proof. Since G

is (Q

, R

, S

)-operator dissipative and G

is (Q

, R

)-operator dissipative it follows that for every T > 0, e

∈ L

, and

∈ L

, Q

+ 2hy

, S

+ he

, R

≥ 0 (7.37)

and

σhy

, Q

+ 2σhy

, S

+ σhe

, R

≥ 0. (7.38)

Now, using e

= u

−y

and e

= u

+ y

, and combining (7.37) and (7.38)

yields

hy,

Qyi

+ 2hy,

Sui

+ hu,

Rui

≥ 0, (7.39)

where u

△

= [u

, u

]

, y

△

= [y

, y

]

, and

△



0 σR



△



−σR

−R

σS



The result now is an immediate consequence of Theorem 7.4.

7.6 Connections Between Input-Output Stability and

Lyapunov Stability

In this section, we provide connections between inpu t-output stability and

Lyapunov stability. Since Lyapunov stability theory deals with state space

dynamical systems we begin by considering nonlinear dynamical systems G

of the form

˙x(t) = F (x(t), u(t)), x(t

) = x

, t ≥ t

, (7.40)

y(t) = H(x(t), u(t)), (7.41)

where x(t) ∈ R

, u(t) ∈ R

, y(t) ∈ R

, F : R

× R

→ R

, and H :

× R

→ R

. For the dynamical system G given by (7.40) and (7.41)

deﬁned on the state space R

, R

and R

deﬁne an input and output space,

respectively, consisting of continuous bounded functions on the semi-inﬁnite

interval [0, ∞). The input and output spaces U and Y are assumed to be

closed un der the shift operator, that is, if u(·) ∈ U (respectively, y(·) ∈ Y),

then the function deﬁned by u

△

= u(t + T ) (respectively, y

△

= y(t + T ))

is contained in U (respectively, Y) for all T ≥ 0. We assume that F (·, ·)

and H(·, ·) are continuously diﬀerentiable mappings in (x, u) and F (·, ·) has

at least one equilibrium so that, without loss of generality, F (0, 0) = 0 and

H(0, 0) = 0.

Theorem 7.6. Consider the n onlinear dynamical system G given by

(7.40) and (7.41). Assume that there exist a continuously diﬀerentiable

NonlinearBook10pt November 20, 2007

484 CHAPTER 7

function V : R

→ [0, ∞) and positive scalars α, β, γ

, γ

such that

αkxk

≤ V (x) ≤ βkxk

, x ∈ R

, (7.42)

′

(x)F (x, 0) ≤ −γ

kxk

, x ∈ R

, (7.43)

′

(x)k ≤ γ

kxk, x ∈ R

. (7.44)

Furth ermore, assume that there exist positive scalars L, η

, and η

such that

kF (x, u) − F(x, 0)k ≤ Lkuk, (x, u) ∈ R

× R

, (7.45)

kH(x, u)k ≤ η

kxk + η

kuk, (x, u) ∈ R

× R

. (7.46)

Then, for every x

∈ R

and p ∈ [1, ∞], G is L

-stable with ﬁn ite gain.

Proof. It f ollows from (7.43)–(7.45) that

′

(x)F (x, u) = V

′

(x)F (x, 0) + V

′

(x)[F (x, u) − F (x, 0)]

≤ −γ

kxk

+ γ

Lkxkkuk, x ∈ R

, u ∈ R

. (7.47)

Now, let u ∈ L

and let x(t), t ≥ 0, denote the solution to (7.40) with

x(0) = 0 and deﬁne W (t)

△

V (x(t)), t ≥ 0. First, consider the case in

which W (t) 6= 0, t > 0. In this case, it follows from (7.42) and (7.47) that

2W (t)

W (t) =

V (x(t))

= V

′

(x(t))F(x(t), u(t))

≤ −γ

kx(t)k

+ γ

Lkx(t)kku(t)k

≤ −

V (x(t)) +

√

1/2

(x(t))ku(t)k

= −

(t) +

√

W (t)ku(t)k, t > 0, (7.48)

which implies that

W (t) +

2β

W (t) ≤

√

ku(t)k, t > 0. (7.49)

Now, multiplying (7.49) by e

2β

, t ≥ 0, yields



2β

W (t)



≤ e

2β

√

ku(t)k, t > 0. (7.50)

Next, since W (0) = V

1/2

(x(0)) = 0, integrating (7.50) yields

W (t) ≤

√

−

2β

(t−τ)

ku(τ)kdτ, t > 0. (7.51)

Now, it follows from (7.51) that there exists a constant γ > 0 su ch that

|||W |||

≤ γ|||u|||

and, since kx(t)k ≤

√

W (t), t ≥ 0, it follows that x(·) ∈ L

The result is now a direct consequence of (7.46). The case in which W (t) = 0,

t ≥ 0, is a straightforward extension of the proof above since W (t) = 0, t ≥ 0,

if and only if x(t) = 0, t ≥ 0.