Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 395

−

x and the required supply is given by V

(x) = x

x, where P

−

and P

are the minimal an d maximal solutions to (5.255), respectively.

Furth ermore, show that there exist α > 0 and β > 0 such that

αkxk

≤ V

(x) ≤ V

(x) ≤ βkxk

, x ∈ R

. (5.256)

Problem 5.29. Consider the nonlinear dynamical system G given by

(5.75) and (5.76), and assume that G is zero-state obs ervable and completely

reachable. Show that if G is input strict passive, then det J(x) 6= 0, x ∈ R

and h en ce, G has relative degree zero.

Problem 5.30. Give a complete proof of Th eorem 5.11.

Problem 5.31. Let G(s) be a real rational matrix transf er function

with in put u(·) ∈ U and output y(·) ∈ Y. Show that G(s) is lossless with

respect to the sup ply rate r(u, y) = 2u

y if and only if He G(ω) = 0 for all

ω ∈ R, w ith ω not a pole of any entry of G(s), and if ω is a pole of any

entry of G(s) it is at most a s imple pole and the residue matrix (Th eorem

5.11) at ω is nonnegative deﬁnite Hermitian. Alternatively, show that G(s)

is lossless with respect to supply rate r(u, y) = γ

u − y

y, γ > 0, if and

only if γ

I − G

∗

(ω)G(ω) = 0 for all ω ∈ R.

Problem 5.32. Let

G(s)

min

∼



A B

C D



be positive real with D + D

> 0, and let P , L, and W , with P > 0, satisfy

(5.151)–(5.153). Show that

−1

(s)

min

∼





where

A = A − BD

−1

B = BD

−1

C = −D

−1

C, and

D = D

−1

, is also

positive real, and P satisﬁes

0 =

P + P

A +

L, (5.257)

0 = P

B −

W , (5.258)

0 =

D +

−

W , (5.259)

where

L = L − W D

−1

C and

W = W D

−1

Problem 5.33. Let

G(s)

min

∼



A B

C 0



be a positive real transfer function. G(s) is a self-dual realization if A+A

≤

NonlinearBook10pt November 20, 2007

396 CHAPTER 5

0 and B = C

. Show that a self-dual realization can be obtained from the

change of co ordinates z = P

1/2

x, where P satisﬁes (5.151) and (5.152), and

x is the internal state of the realization of G(s).

Problem 5.34. Consider the linear dynamical system

G(s)

min

∼



A B

C D



with input u(·) ∈ U and output y(·) ∈ Y. Assume that A is asymptotically

stable. Show that the following statements are equivalent:

i) There exists ε > 0 s uch that G(ω) + G

∗

(ω) ≥ εI for all ω ∈ R.

ii) There exists γ > 0 and a function β : R

→ R, β(0) = 0, such that for

all T ≥ 0,

(t)y(t)dt ≥ β(x

) + γ

(t)u(t)dt. (5.260)

iii) There exists ε > 0 such that G(ω −ε) + G

∗

(ω −ε) ≥ 0 f or all ω ∈ R.

iv) G(ω) + G

∗

(ω) > 0, for all ω ∈ R, and

lim

ω →∞

[G(ω) + G

∗

(ω)] > 0. (5.261)

Problem 5.35. Consider the controlled nonlinear oscillator given by

the undamped Duﬃng equation

¨x(t) + (2 + x

(t))x(t) = u(t), x(0) = x

, ˙x(0) = ˙x

, t ≥ 0, (5.262)

y(t) = ˙x(t). (5.263)

Show that the input-output map from u to y is lossless with respect to the

supply rate r(u, y) = uy.

Problem 5.36. Consider the controlled nonlinear damped oscillator

given by

¨x(t) + η(x(t), ˙x(t))[ ˙x(t) + x(t)] = u(t), x(0) = x

, ˙x(0) = ˙x

, t ≥ 0,

(5.264)

y(t) = x(t) + ˙x(t), (5.265)

where η(x, ˙x) = 2 + (x + ˙x)

. Show that th e input-output map from u to y

is exponentially passive.

Problem 5.37. Consider the controlled nonlinear system

˙x

(t) = x

(t), x

(0) = x

, t ≥ 0, (5.266)

˙x

(t) = −(1 + x

(t))x

(t) − x

(t) + x

(t)u(t), x

(0) = x

, (5.267)

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 397

y(t) = x

(t)x

(t). (5.268)

Show that the input-output map from u to y is nonexpansive w ith γ ≥ 1.

(Hint: Use the storage f unction V

, x

) = αx

+ βx

, where α, β > 0 are

parameters to be chosen.)

Problem 5.38. Consider the linear dynamical system

˙x(t) = −x(t) + u(t), x(0) = x

, t ≥ 0, (5.269)

y(t) = x(t) + u(t). (5.270)

Show that (5.269) and (5.270) is passive. Find V

(x), V

(x), and V

(x) for

(5.269) and (5.270).

Problem 5.39. Consider the controlled linear system

˙x(t) = −x(t) + u(t), x(0) = x

, t ≥ 0, (5.271)

y(t) = x(t). (5.272)

Show that (5.271) and (5.272) is nonexpansive with γ ≥ 1.

Problem 5.40. Consider the scalar dynamical system

˙x(t) = −x(t) + 2u(t), x(0) = x

, t ≥ 0, (5.273)

y(t) = tan

−1

(x(t)). (5.274)

Show that (5.273) and (5.274) is output strict p assive.

Problem 5.41. Consider the nonlinear dynamical sy s tem in polar

co ordinates given by

˙r(t) = r(t)(r

(t) −1)(r

(t) −4) + r(t)(r

(t) − 4)u(t),

r(0) = r

, t ≥ 0, (5.275)

θ(t) = 1, θ(0) = θ

, (5.276)

y(t) = r

(t) − 1. (5.277)

Show that th e set D

= {(r, θ) ∈ R × R : r = 1} is invariant und er the

uncontrolled (i.e., u(t) ≡ 0) d ynamics and D

is asymptotically stable. I n

addition, s how that the largest domain of attraction (with respect to D

) of

the uncontrolled system (5.275) and (5.276) is given by D

= {(r, θ) ∈ R ×

R : 0 < r < 2}. Finally, show that (5.275)–(5.277) is nonexpansive with γ ≥

1. (Hint: Use the storage function V

(r, θ) = −

ln r

−

ln(4 −r

) +

ln 3

with (r, θ) = (1, 0) being the equilibriu m solution of (5.275) and (5.276).)

Problem 5.42. Consider the nonlinear dynamical system

˙x(t) = x(t) + u(t), x(0) = x

, t ≥ 0, (5.278)

NonlinearBook10pt November 20, 2007

398 CHAPTER 5

y(t) = −

αx(t)

1 + x

(t)

, (5.279)

where α > 0. Show that V

(x) = α(

− tan

−1

)) satisﬁes the dissipation

inequality (5.16) with r(u, y) = 2uy and yet the zero solution x(t) ≡ 0 of

the undisturbed system (5.278) is unstable. Why does this contradict i) of

Proposition 5.2?

Problem 5.43. Consider the nonlinear dynamical system G given by

(5.75) and (5.76), and assume G is completely reachable and zero state

observable. Furthermore, assume G is p assive and J(x)+J

(x) > 0, x ∈ R

Show that V

(x) and V

(x) satisfy

0 = V

′

(x)f(x) + [

′

(x)G(x) − h

(x)]

·[J(x) + J

(x)]

−1

[

′

(x)G(x) − h

(x)]

, x ∈ R

, (5.280)

where V (·) is positive deﬁnite and V (0) = 0. (Hint: First show that

(s)y(s)ds = V (x(t)) −V (x(t

)) +



1 u

(s)





A(x(s)) B(x(s))

(x(s)) C(x(s))



u(s)



ds,

where A(x)

△

= −V

′

(x)f(x), B(x)

△

= h

(x) −

′

(x)G(x), and C(x)

△

= J(x) +

(x).)

Problem 5. 44. Consider th e nonlinear time-varying dynamical system

G given by

˙x(t) = f (t, x(t)) + G(t, x(t))u(t), x(t

) = x

, t ≥ t

, (5.281)

y(t) = h(t, x(t)) + J(t, x(t))u(t), (5.282)

where x(t) ∈ D ⊆ R

, D is an open set with 0 ∈ D, u(t) ∈ U ⊆ R

, y(t) ∈

Y ⊆ R

, f : [t

, ∞)×D → R

, G : [t

, ∞)×D → R

n×m

, h : [t

, ∞)×D → Y ,

and J : [t

, ∞) × D → R

l×m

. Here, assume that f(·, ·), G(·, ·), h(·, ·), and

J(·, ·) are piecewise continuous in t and continuously diﬀerentiable in x on

, ∞) × D. The available storage and required supply for n onlinear time-

varying dynamical systems are deﬁned as

, x

)

△

= − inf

u(·), T ≥t

r(u(t), y(t))dt (5.283)

and

, x

)

△

= inf

u(·), T ≥t

r(u(t), y(t))dt. (5.284)

Assuming that G is completely reachable and V

(t, x) and V

(t, x) are

continuously diﬀerentiable on [0, ∞) × D, show that G is passive if and

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 399

only if there exists an almost everywhere continuously diﬀerentiable function

: [0, ∞) × D → R such that V

(t, x) ≥ 0, (t, x) ∈ [0, ∞) × D, V

(t, 0) = 0,

t ∈ [0, ∞), and for all (t, x) ∈ [0, ∞) ×D,

∂V

(t,x)

∂x

f(t, x) +

∂V

(t,x)

∂t

∂V

(t,x)

∂x

G(t, x) − h

(t, x)

∂V

(t,x)

∂x

− h(t, x) −(J(t, x) + J

(t, x))

≤ 0. (5.285)

Problem 5.45. Consider the nonlinear dynamical system G given by

(5.7) and (5.8). Assume that G is passive with a two-times continuously

diﬀerentiable storage function V

(·). Show that

′

(x)F (x, 0) ≤ 0, x ∈ D, (5.286)

′

(x)G(x, 0) = H

(x, 0), x ∈ Q, (5.287)

i=1

∂

∂u

(x, 0)

∂V

∂x

≤

∂H

∂u

(x, 0) +



∂H

∂u

(x, 0)



, x ∈ Q, (5.288)

where Q = {x ∈ D : V

′

(x)F (x, 0) = 0} and F

(x, u) denotes the ith

component of F (x, u).

Problem 5.46. Consider the govern ing equations of motion of an n-

degree-of-freedom d ynamical system given by the Euler-Lagrange equation



∂L

∂ ˙q

(q, ˙q)



−



∂L

∂q

(q, ˙q)



= u, (5.289)

where q ∈ R

represents the generalized system positions, ˙q ∈ R

represents

the generalized system velocities, L : R

× R

→ R denotes the system

Lagrangian given by L(q, ˙q) = T (q, ˙q) −V (q), where T : R

×R

→ R is the

system kinetic energy and V : R

→ R is the sys tem potential energy, and

u ∈ R

is the vector of generalized forces acting on the system.

i) Show that the Euler-Lagrange equ ation can be equivalently character-

ized by the state equations

˙q =



∂H

∂p

(q, p)



, (5.290)

˙p = −



∂H

∂q

(q, p)



+ u, (5.291)

where p ∈ R

represents the system generalized momenta and H :

×R

→ R denotes the Legendre transformation given by H(q, p) =

˙q

p − L(q, ˙q).

ii) Show that the rate of change in system energy is equal to the external

power inpu t, that is,

H(q, p) = ˙q

u, (5.292)

NonlinearBook10pt November 20, 2007

400 CHAPTER 5

and h en ce, H (q, p) is a storage function for (5.290) and (5.291).

iii) Show that if V (q) is bounded from below, then the system input-

output map from generalized forces u to generalized velocities ˙q is

lossless, that is,

0 =

˙q

(t)u(t)dt, (5.293)

for all T ≥ 0 with (q(0), ˙q(0)) = (q(T ), ˙q(T )) = (0, 0).

iv) For dynamical n degree-of-freedom systems with internal dissipation

the Euler-Lagrange equations (5.289) take the form



∂L

∂ ˙q

(q, ˙q)



−



∂L

∂q

(q, ˙q)





∂R

∂ ˙q

( ˙q)



= u, (5.294)

where R : R

→ R represents the Rayleigh dissipation function

satisfying

∂R

∂ ˙q

( ˙q) ˙q ≥ 0, ˙q ∈ R

. Show that in this case (5.292) becomes

H(q, p) = −

∂R

∂ ˙q

( ˙q) ˙q + u

˙q, (5.295)

and the system input-output map from generalized forces u to

generalized velocities ˙q is passive, that is,

0 ≤

˙q

(t)u(t)dt, (5.296)

for all T ≥ 0 with (q(0), ˙q(0)) = (0, 0).

v) Show that if (5.294) is f ully damped, that is, there exists ε > 0 such

that

∂R

∂ ˙q

( ˙q) ˙q ≥ ε ˙q

˙q, ˙q ∈ R

, then (5.294) is output strict passive.

vi) Show that (5.294) can be interpreted as the negative feedback

interconnection of two passive systems G

and G

with input-output

pairs (ˆu, ˙q) and ( ˙q,

∂R

∂ ˙q

), respectively, where ˆu = u −



∂R

∂ ˙q



vii) Characterize the system dynamics for G

and G

in vi).

viii) Show that the zero solution to (5.289) or, equivalently, (5.290) and

(5.291) is asymptotically stable if u = −K

˙q, where K

∈ R

n×n

and

satisﬁes K

+ K

> 0.

ix) Show that with u = −K

˙q + ˆu, where K

∈ R

n×n

and satisﬁes K

> 0, the input-output map from ˆu to ˙q is output strict p assive.

x) Show that if T (q, ˙q) =

˙q

M(q) ˙q, where M(q) > 0, q ∈ R

, is the

system in ertia matrix function, then (5.289) becomes

M(q)¨q + C(q, ˙q) ˙q + g(q) = u, (5.297)

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 401

where g(q) =

∂V

∂q

(q)

and C(q, ˙q)

(i,j)

k=1

ijk

(q) ˙q

, where i, j =

1, . . . , n and

ijk

(q) =



∂M

(j,k)

(q)

∂q

∂M

(k,i)

(q)

∂q

−

∂M

(i,j)

(q)

∂q



. (5.298)

xi) Show that

M(q) −2C(q, ˙q) is skew-symmetric for every q, ˙q ∈ R

xii) Show that

M(q) −2C(q, ˙q) is skew-symmetric if and only if

M(q) = C(q, ˙q) + C

(q, ˙q).

xiii) Show that the available storage of the dynamical system (5.297) is

bounded above by

˙q(0)

M(q(0)) ˙q(0) + V (q(0)).

xiv) Show that the required supply of the dynamical system (5.297) is

bounded below by

˙q(0)

M(q(0)) ˙q(0) + V (q(0)).

xv) For C(q, ˙q) ≡ 0 show that the available storage and the required supply

of (5.297) are equal and is given by

˙q(0)

M(q(0)) ˙q(0) + V (q(0)).

Problem 5.47. Consider the govern ing equations of motion of an n-

degree-of-freedom d ynamical system given by Hamiltonian system

˙q =



∂H

∂p

(q, p)



, (5.299)

˙p = −



∂H

∂q

(q, p)



+ G(q)u, (5.300)

y = G

(q)



∂H

∂p

(q, p)



, (5.301)

where q ∈ R

, p ∈ R

, and H : R

× R

→ R are as in Problem 5.46,

and u ∈ R

, y ∈ R

, and G : R

→ R

n×m

. Show that if (5.299)–(5.301)

is zero-state observable, then the zero solution of (5.299) and (5.300), with

u = −y, is asymptotically stable.

Problem 5.48. Consider the port-controlled Hamiltonian s ystem

˙x(t) = J(x(t))



∂H

∂x

(x(t))



+ G(x(t))u(t), x(0) = x

, t ≥ 0, (5.302)

y(t) = G

(x(t))



∂H

∂x

(x(t))



(5.303)

where x ∈ D ⊆ R

, u, y ∈ R

, H : D → R, G : D → R

n×m

, and J :

D → R

n×n

and satisﬁes J(x) = − J

(x). Show that if (5.302) and (5.303)

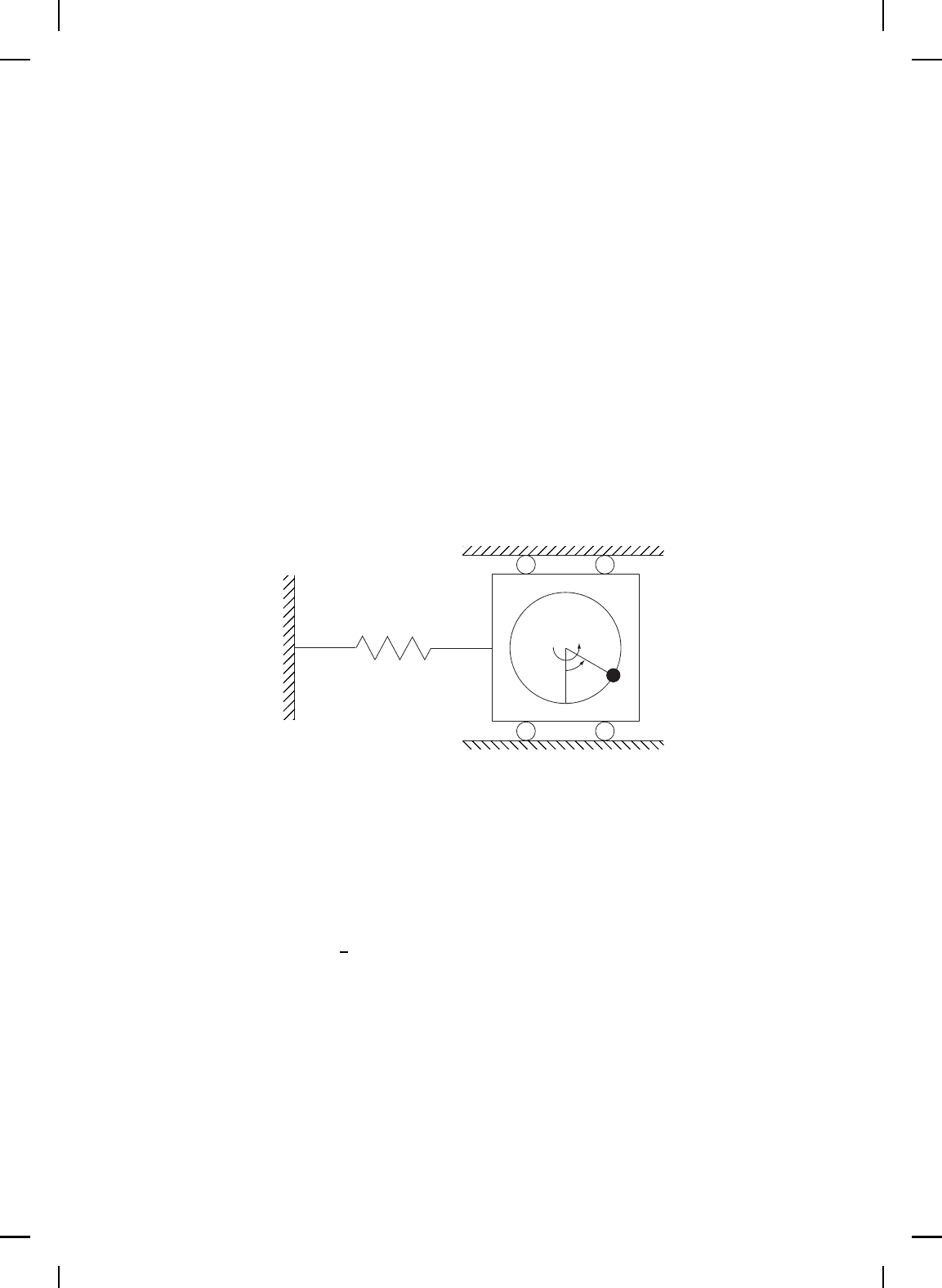
NonlinearBook10pt November 20, 2007

402 CHAPTER 5

is zero-state observable, then the zero solution x(t) ≡ 0 to (5.302), with

u = −y, is asymptotically stable.

Problem 5.49. Consider the rotational/translational nonlinear dyna-

mical system shown in Figure 5.11 with oscillator cart mass M, linear spring

stiﬀness k, rotational mass m, mass moment of inertia I located a distance

e from the center of mass of th e cart, and inpu t torque N. Assume that the

motion is constrained to the horizontal plane.

i) Using the Euler-Lagrange equations given by (5.289) show that the

governing n on linear dynamic equations of motion are given by

(M + m)¨q + kq = −me(

θ cos θ −

sin θ), (5.304)

(I + me

)

θ = −me¨q cos θ + N, (5.305)

where q, ˙q, θ, and

θ denote, respectively, the translational position

and velocity of the cart and the angu lar position and velocity of the

rotational mass.

Figure 5.11 Rotational/translational nonlinear dynamical sy stem.

ii) Show that with output y =

θ and input u = N the sy s tem is passive

but not zero-state obs ervable.

iii) Show that with u = −k

θ + ˆu, where k

> 0, the new system with

output y =

θ and input ˆu is p assive and zero-state observable with

positive-deﬁnite storage function

(q, ˙q, θ,

θ) =

[kq

+ (M + m) ˙q

+ k

+ (I + me

)

+ 2me ˙q

θ cos θ].

(5.306)

Problem 5.50. Consider the linear matrix second-order dynamical

system given by

M ¨q(t) + C ˙q(t) + Kq(t) = Bu(t), q(0) = q

, ˙q(0) = ˙q

, t ≥ 0, (5.307)

y(t) = B

˙q(t), (5.308)

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 403

where q, ˙q, ¨q ∈ R

represent generalized position, velocity, and acceleration

co ordinates, respectively, u ∈ R

is a force input, y ∈ R

is a velocity

measurement, M , C, and K are inertia, damping, and stiﬀness matrices,

respectively, and B ∈ R

n×m

is determined by the location of the system

input-output topology. Assume that M > 0, C ≥ 0, and K ≥ 0.

i) Show that the input-output map from force inputs u to the velocity

measurements y, w ith q

= 0 and ˙q

= 0, is given by y(s) = G(s)u(s),

where

G(s) ∼







0 I

−M

−1

K −M

−1

 

−1





0 B







. (5.309)

ii) Show that G(s) is positive real.

iii) Show that (5.167)–(5.169) hold with

P =



K 0

0 M



, L =



√

1/2



, W = 0.

iv) Construct a Lyapunov function to sh ow that if C ≥ 0 and K > 0, then

(5.307) with u(t) ≡ 0 is Lyapunov stable.

v) Construct a L yapunov fu nction to show that if C > 0 and K ≥ 0, then

(5.307) with u(t) ≡ 0 is semistable (see Problem 3.44).

vi) Construct a Lyapunov function to sh ow that if C > 0 and K > 0, then

(5.307) with u(t) ≡ 0 is asymptotically stable.

vii) Construct a Lyapunov fu nction to show that if K > 0, C ≥ 0, and

rank[C KM

−1

C ··· (KM

−1

)

n−1

C] = n, then (5.307) with u(t) ≡ 0 is

asymptotically stable.

viii) Show that if C in (5.307) is replaced by C + G, where G = −G

captures system gyroscopic eﬀects, and C > 0, K > 0, then (5.307)

with u(t) ≡ 0 remains asymptotically stable.

ix) Show that with q

= 0 and ˙q

= 0, u

y ≥ 0.

Problem 5.51. Consider the nonlinear dynamical system representing

a controlled rigid spacecraft given by

˙x

(t) = I

(t)x

(t) +

(t), x

(0) = x

, t ≥ 0, (5.310)

˙x

(t) = I

(t)x

(t) +

(t), x

(0) = x

, (5.311)

˙x

(t) = I

(t)x

(t) +

(t), x

(0) = x

, (5.312)

where I

= (I

− I

)/I

, I

= (I

− I

)/I

, I

= (I

− I

)/I

, and I

, I

and I

are the principal moments of inertia of the spacecraft. Show that the

NonlinearBook10pt November 20, 2007

404 CHAPTER 5

input-output map from u = [u

, u

]

to y = x = [x

, x

]

is lossless

with respect to the supp ly rate r(u, y) = 2u

y. Furthermore, show that th e

zero solution x(t) ≡ 0 to (5.310)–(5.312) is globally asymptotically stable if

u = −Kx, w here K ∈ R

3×3

and satisﬁes K + K

> 0. Alternatively, show

that if u = −φ(x) and satisﬁes x

φ(x) > 0, x 6= 0, then the zero solution

x(t) ≡ 0 to (5.310)–(5.312) is also globally asymptotically stable. Finally, if

φ : R

→ R

is such that φ(x) = [φ

), φ

)]

, how would you

pick φ

), i = 1, 2, 3, so as to maximize the decay rate of the Lyapunov

function candidate V (x) = I

+ I

Problem 5.52. Consider a thermodynamic system at a uniform

temperature. The ﬁrst law of thermodynamics states that during any cycle

that a system und ergoes, the cyclic integral of the heat is proportional to

the cyclic integral of the work, that is,

dQ =

dW, (5.313)

where

dQ represents the net heat transfer during the cycle and

represents the net work during the cycle. J is a proportionality factor,

which depends on the units used for work and heat. Here, assume SI units

so that J = 1. The second law of thermodynamics states th at the transfer

of heat from a lower temperature level (source) to a higher temperature level

(sink) requires the in put of add itional work or energy, or, using Clausius’

inequality,

≤ 0, (5.314)

where

represents the system entropy and T represents the absolute

system temperature. Writing the ﬁrst and second laws as rate equations

and assuming that every admissible system input and every initial system

state yield locally integrable work and heat generation functions, show

that the ﬁrst and second laws of thermodynamics can be formulated using

cyclo-dissipative system theoretic notions with appropriate virtual storage

functions and supply rates (see Problems 5.3–5.5). Use the convention that

the work done by the system and the heat delivered to the system are

positive.

Problem 5.53. Let α, β ∈ R be such th at α ≤ β and let σ : R → R

with σ(0) = 0. Show that the following statements are equivalent:

i) α ≤ σ(u)/u ≤ β, u ∈ R, u 6= 0.

ii) αu

≤ σ(u)u ≤ βu

, u ∈ R.

iii) (σ(u) − αu)(σ(u) − βu) ≤ 0, u ∈ R.