Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

STABILITY OF FEEDBACK SYSTEMS 415

corresponding Lyapunov derivative is given by

V (x, x

) =

(x) + σ

)

≤ r(u, y) + σr

, y

)

= y

Qy + 2y

Su + u

Ru + σ(y

+ 2y

+ u

)









≤ 0, (x, x

) ∈ R

×R

which implies that the negative feedback interconnection of G and G

Lyapunov stable. Next, let R

△

= {(x, x

) ∈ R

× R

V (x, x

) = 0} and

note that

V (x, x

) = 0 if and only if (y, y

) = (0, 0). Now, since G and G

are zero-state observable it follows that M = {(0, 0)} is the largest invariant

set contained in R. Hence, it follows fr om Theorem 3.5 that (x(t), x

(t)) →

M = {(0, 0)} as t → ∞. Finally, global asymptotic stability follows from

the fact that V

(·) and V

(·) are, by assumption, r adially unbounded, and

hence, V (x, x

) → ∞ as k(x, x

)k → ∞.

The following two corollaries are a direct consequence of Theorem

6.2. For both results note that if a nonlinear dynamical system G is

dissipative (respectively, exponentially dissipative) with respect to a supply

rate r(u, y) = u

y − εu

u − ˆεy

y, where ε, ˆε ≥ 0, then with κ(y) = ky,

where k ∈ R is su ch that k(1 − εk) < ˆε, r(u, y) = [k(1 − εk) − ˆε]y

y < 0,

y 6= 0. Hence, if G is zero-state observable it follows from Theorem 5.6 that

all storage functions (respectively, exponential storage functions) of G are

positive deﬁnite. For the next result, we assume that all storage functions

of G and G

are continuously diﬀerentiable.

Corollary 6.1. Consider the closed-loop system consisting of the

nonlinear dynamical systems G given by (6.1) and (6.2) and G

given by

(6.3) and (6.4), and assume G and G

are zero-state observable. Then the

following statements hold:

i) I f G is passive, G

is exponentially passive, and rank[G

, 0)] = m,

∈ R

, th en the negative feedback interconnection of G and G

asymptotically stable.

ii) If G and G

are exponentially passive with storage functions V

(·) and

(·), respectively, such that (6.5) and (6.6) hold, then the n egative

feedback interconnection of G and G

is exponentially stable.

iii) If G is nonexpansive w ith gain γ > 0, G

is exponentially nonexpansive

with gain γ

> 0, rank[G

, 0)] = m, u

∈ R

, and γγ

≤ 1, then

the negative feedback interconnection of G and G

is asymptotically

stable.

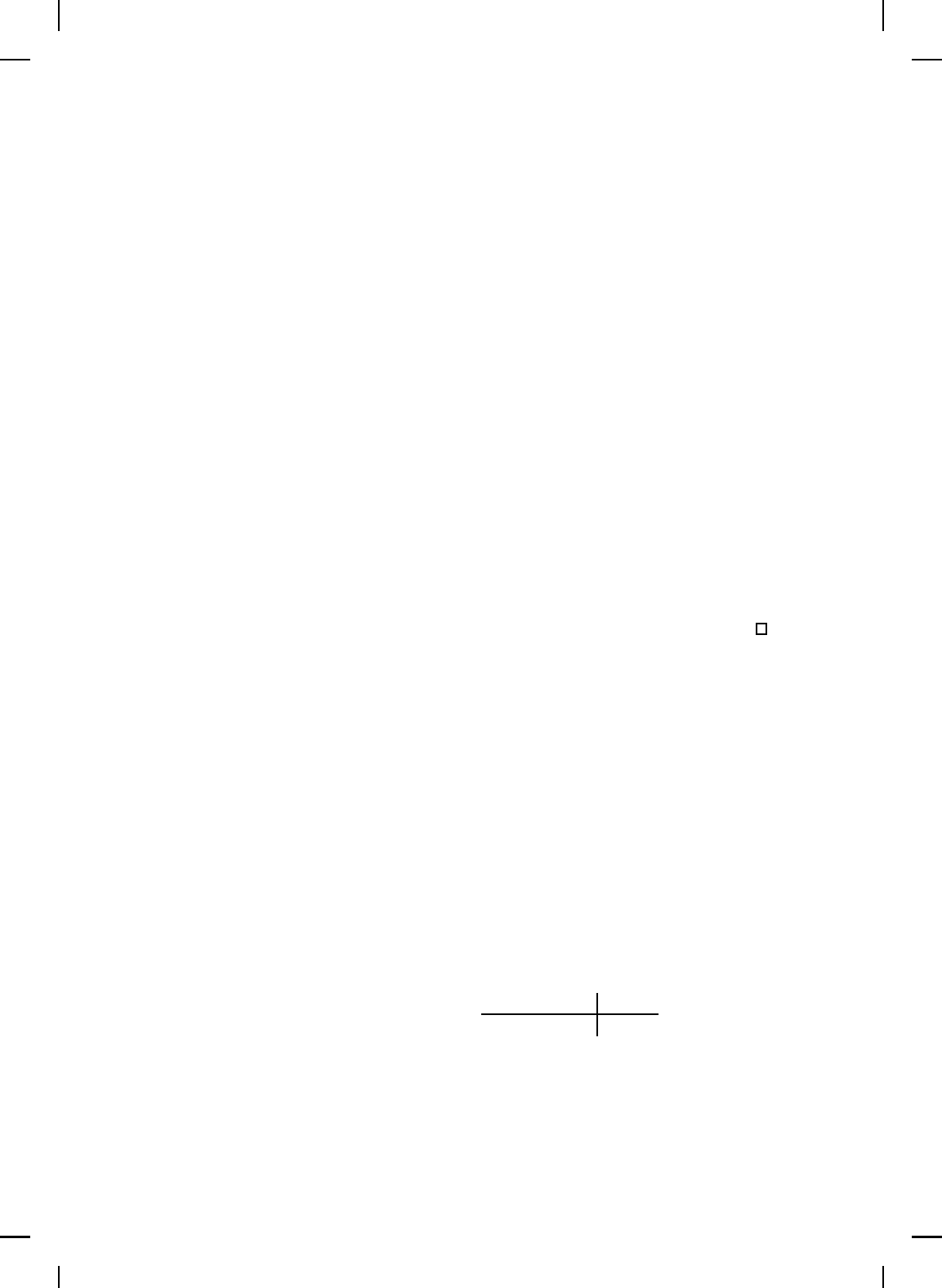
NonlinearBook10pt November 20, 2007

416 CHAPTER 6

iv) If G and G

are exponentially nonexpansive with storage fun ctions V

(·)

and V

(·), respectively, such that (6.5) and (6.6) hold, and with gains

γ > 0 and γ

> 0, respectively, such that γγ

≤ 1, then the negative

feedback interconnection of G and G

is exponentially stable.

v) If G is passive and G

is input-output strict passive, then the negative

feedback interconnection of G and G

is asymptotically stable.

vi) If G and G

are input strict passive, then the negative feedback

interconnection of G and G

is asymptotically stable.

vii) If G and G

are outpu t strict passive, then the negative feedback

interconnection of G and G

is asymptotically stable.

Proof. The proof is a direct consequence of Theorem 6.2. Speciﬁcally,

i) and ii) follow from Theorem 6.2 with Q = Q

= 0, S = S

= I

, and

R = R

= 0, while iii) and iv) follow from Theorem 6.2 with Q = −I

S = 0, R = γ

, Q

= −I

, S

= 0, and R

= γ

. Statement v) follows

from Theorem 6.2 with Q = 0, S = I

, R = 0, Q

= −ˆεI

, S

= I

, and

= −εI

, where ε, ˆε > 0. Statement vi) follows from Theorem 6.2 with

Q = 0, S = I

, R = −εI

, Q

= 0, S

= I

, and R

= −ˆεI

, where

ε, ˆε > 0. Finally, vii) follows from Theorem 6.2 with Q = −εI

, S = I

R = 0, Q

= −ˆεI

, S

= I

, and R

= 0, where ε, ˆε > 0.

Example 6.1. Consider the nonlinear d y namical system

˙x(t) = Ax(t) −Bφ(Cx(t)), x(0) = x

, t ≥ 0, (6.8)

where x(t) ∈ R

, t ≥ 0, A ∈ R

n×n

, B ∈ R

n×m

, C ∈ R

m×n

, (A, C) is

observable, and φ(·) ∈ Φ

, where

△

= {φ : R

→ R

: φ(0) = 0, φ(y) = [φ

), . . . , φ

)]

, y ∈ R

> 0, y

6= 0, i = 1, . . . , m}. (6.9)

Note that (6.8) can be rewritten as a negative feedback interconnection of a

linear dynamical system given by the transfer function G(s) = C(sI −A)

−1

and a memoryless feedback time-invariant nonlinearity φ(·) (see Figure 6.2

(a)). Equivalently, we can rewrite the above feedback interconnection as a

negative feedback interconnection of a linear d ynamical system given by the

transfer function

G(s) and a nonlinear dynamical system G

(see Figure 6.2

(b)), wh ere

G(s)

△

= (M + Ns)G(s) ∼



A B

MC + NCA NCB



, (6.10)

M, N ∈ R

m×m

, M, N > 0 are diagonal, and G

is given by

ˆx(t) = −MN

−1

ˆx(t) + N

−1

ˆu(t), ˆx(0) = 0, t ≥ 0, (6.11)

NonlinearBook10pt November 20, 2007

STABILITY OF FEEDBACK SYSTEMS 417

ˆy(t) = φ(ˆx(t)), (6.12)

where ˆx(t), ˆu(t), ˆy(t) ∈ R

, t ≥ 0, and ˆu(t) = (MC + NCA)x(t).

Now, consider the function

V : R

→ R

given by

V (ˆx) = 2

i=1

ˆx

(i,i)

(σ)dσ, (6.13)

and n ote that

V (ˆx) > 0, ˆx ∈ R

, ˆx 6= 0,

V (0) = 0, and

V (ˆx(t)) = 2

i=1

(i,i)

φ(ˆx

(t))

ˆx

(t)

= 2

ˆx

(t)Nφ(ˆx(t))

= −2ˆx

(t)Mφ(ˆx(t)) + 2ˆu

(t)φ(ˆx(t))

≤ 2ˆu

(t)ˆy(t), t ≥ 0, (6.14)

which implies that

V (ˆx) is a storage function for G

, and hence, G

is a

passive dynamical system. Now, it follows from i) of C orollary 6.1 that

G(s) is strictly positive real, then the negative feedback interconnection

G(s) and G

is asymptotically stable or, equivalently, the zero solution

x(t) ≡ 0 to (6.8) is asymptotically stable f or all φ ∈ Φ

. Hence, it follows

from Theorem 5.14 that

G(s) is strictly positive real if and only if th ere

exist matrices P ∈ R

n×n

, P > 0, L ∈ R

p×n

, and W ∈ R

p×m

, with P

positive deﬁnite, and a scalar ε > 0 su ch that

0 = A

P + P A + εP + L

L, (6.15)

0 = B

P − MC − NCA + W

L, (6.16)

0 = NCB + B

N − W

W. (6.17)

Now, V (x, ˆx) = x

P x +

V (ˆx) or, equivalently,

V (x) = x

P x + 2

i=1

(i,i)

(σ)dσ, (6.18)

since ˆu = y, is a Lyapunov function for (6.8). △

Example 6.2. Consider the controlled undamped Duﬃng equation

given by

˙x

(t) = x

(t), x

(0) = x

, t ≥ 0, (6.19)

˙x

(t) = −[2 + x

(t)]x

(t) + u(t), x

(0) = x

, (6.20)

y(t) = x

(t). (6.21)

Deﬁning x = [x

, x

]

, (6.19)–(6.21) can be written in s tate space form

(6.1) and (6.2) with f(x) = [x

, −(2 + x

]

, G(x) = [0, 1]

, h(x) = x

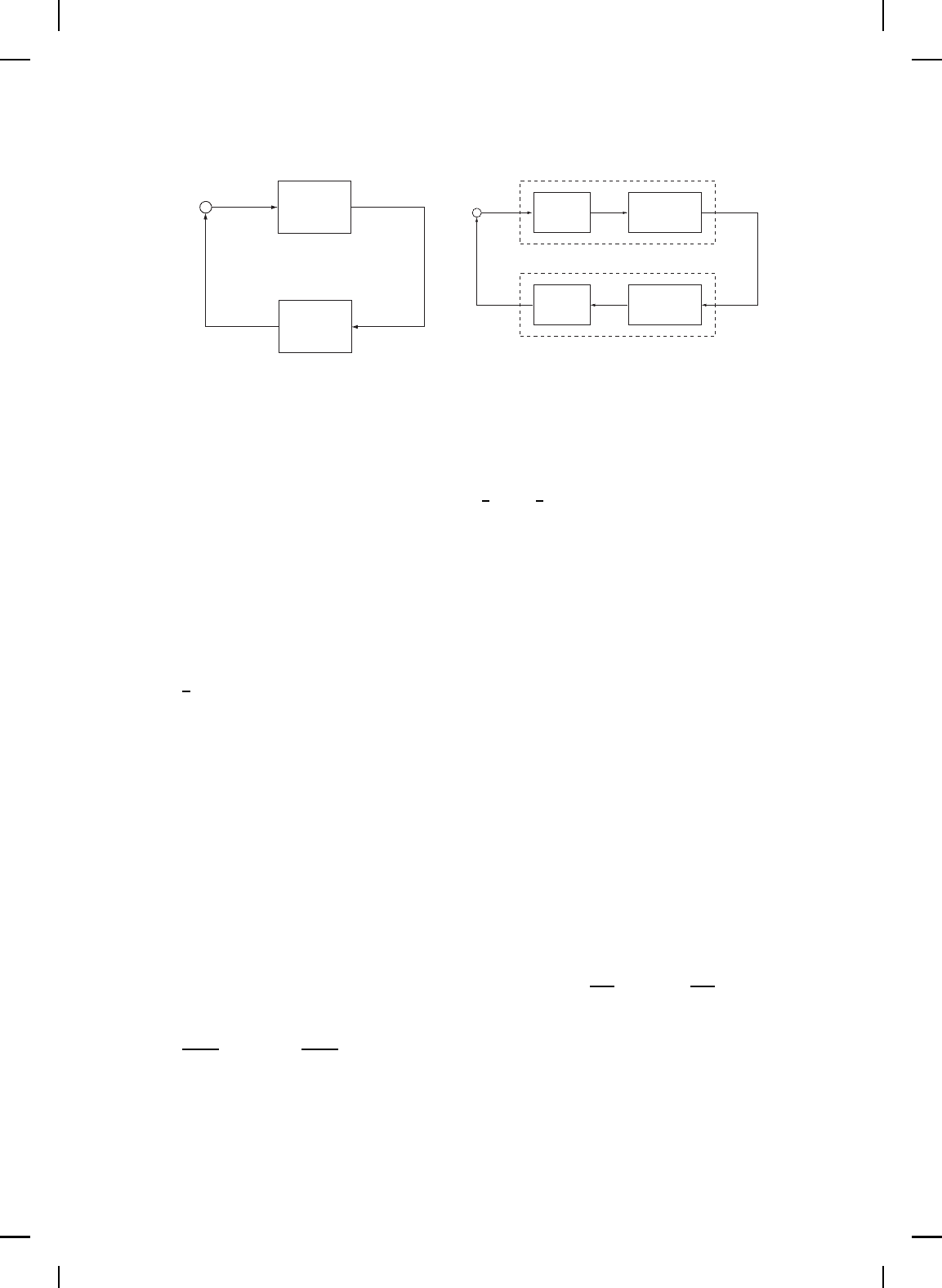
NonlinearBook10pt November 20, 2007

418 CHAPTER 6

G(s)

φ(·)

−

G(s)

M + Ns

φ(·) (M + Ns)

−1

u ˆu

G(s)

−

(a) (b)

Figure 6.2 Feedback interconnection representation of an uncertain system.

and J(x) = 0. With V

(x) = x

, ℓ(x) ≡ 0, and W(x) ≡

0, it follows from Corollary 5.2 that (6.19)–(6.21) is passive. Now, usin g

Corollary 6.1 we can design a reduced-order linear dynamic compensator to

asymptotically s tabilize (6.19) and (6.20). Speciﬁcally, it follows from i) of

Corollary 6.1 that if G

given by (6.3) and (6.4) is exponentially passive with

rank[G

(0)] = 1, then the negative feedback interconnection of G given by

(6.19)–(6.21) and G

is asymptotically stable. Here, we construct a reduced-

order linear dynamic compensator G

given by (6.3) and (6.4) with f

) =

−10x

, G

) = 5, h

) = 6x

, and J

) ≡ 0. Note th at with V

) =

, ε = 20, ℓ(x

) ≡ 0, and W(x

) ≡ 0, it follows from Corollary 5.4

that G

is exponentially passive. Hence, Corollary 6.1 guarantees that the

negative feedback interconnection of G and G

is globally asymptotically

stable. Figures 6.3 and 6.4 compare the time responses of the position x

and velocity x

, respectively, for the open-loop and closed-loop systems for

an initial condition [x

, x

]

= [1, 0.5]

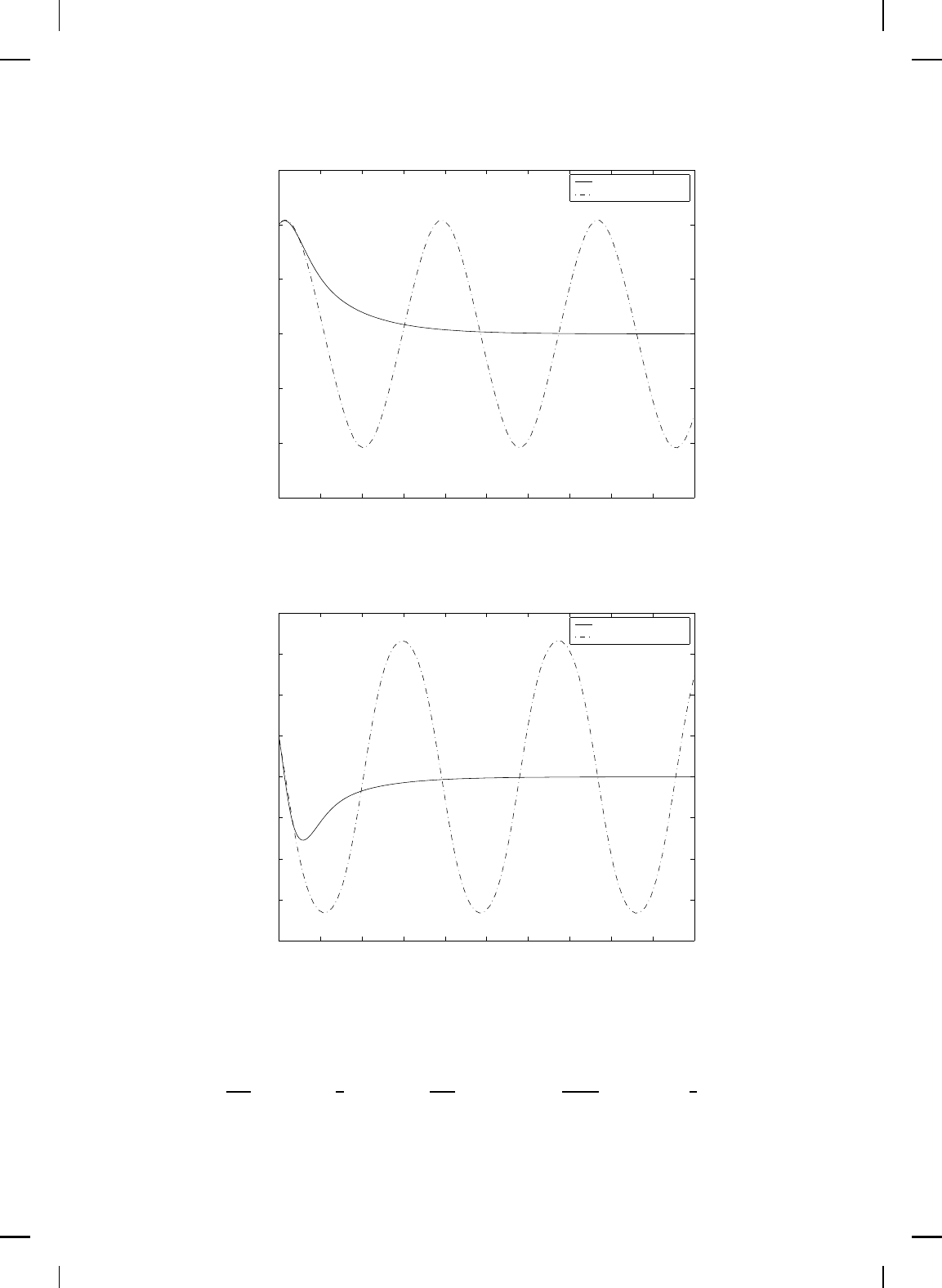
. Figure 6.5 compares the control

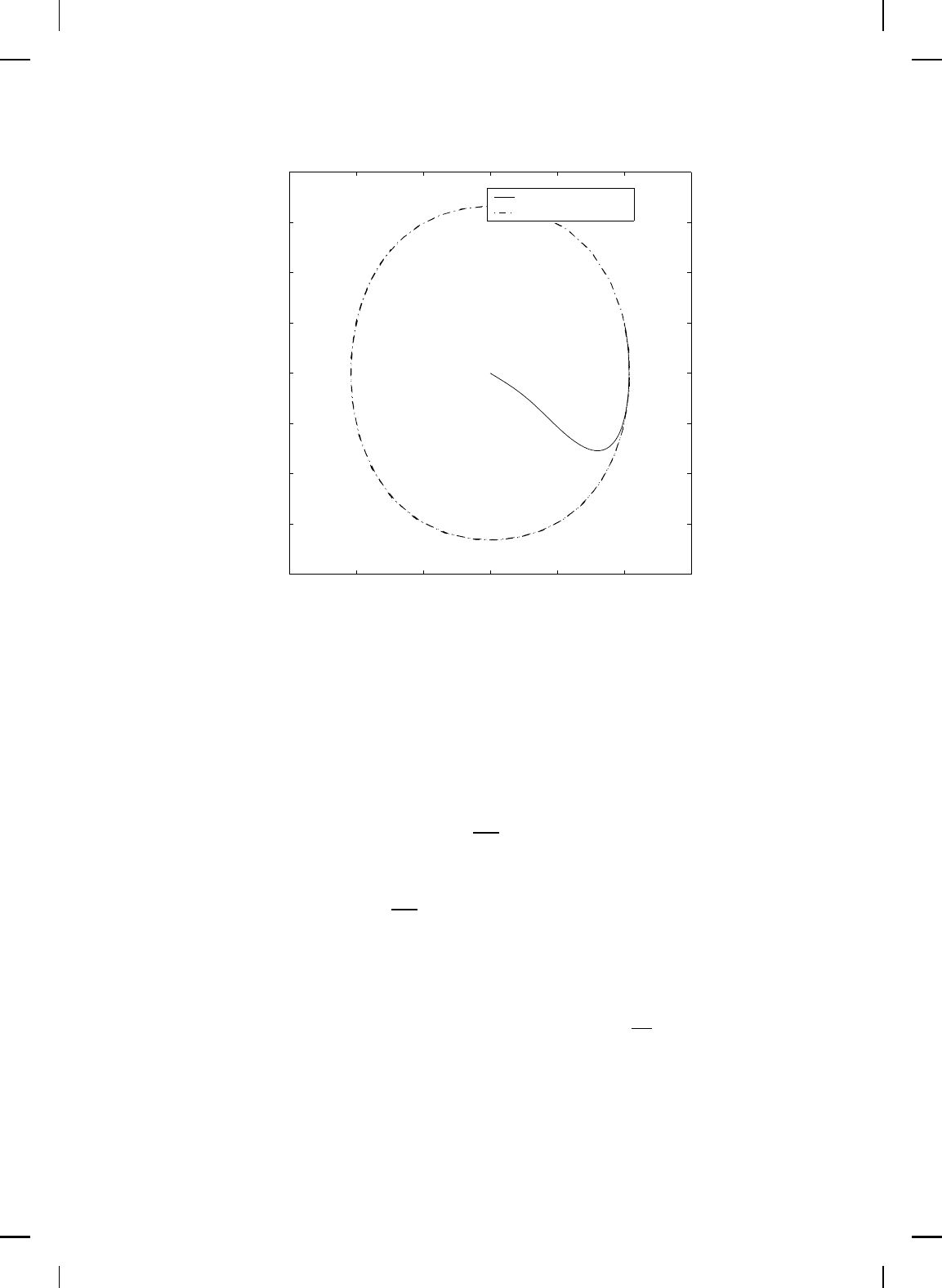
eﬀort versus time and Figure 6.6 gives the phase portraits of the open-loop

and closed-loop systems. △

Corollary 6.2. Consider the closed-loop system consisting of the

nonlinear dynamical systems G given by (6.1) and (6.2) and G

given by

(6.3) and (6.4). Let a, b, a

, b

, δ ∈ R be such that b > 0, 0 < a + b,

0 < 2δ < b − a, a

= a + δ, and b

= b + δ, let M ∈ R

m×m

be positive

deﬁnite, and assume G and G

are zero-state observable. If G is dissipative

with respect to the supply rate r(u, y) = u

My +

a+b

My +

a+b

and has a continuously diﬀerentiable radially unbounded storage function,

and G

is dissipative with respect to the su pply rate r

, y

) = u

−

and has a continuously diﬀerentiable radially

unbounded storage function, then the negative feedback interconnection of

G and G

is globally asymptotically stable.

NonlinearBook10pt November 20, 2007

STABILITY OF FEEDBACK SYSTEMS 419

0 1 2 3 4 5 6 7 8 9 10

−1.5

−1

−0.5

0.5

1.5

time

Position

Dynamic Feedback

Open−Loop

Figure 6.3 Position versus time.

0 1 2 3 4 5 6 7 8 9 10

−2

−1.5

−1

−0.5

0.5

1.5

time

Velocity

Dynamic Feedback

Open−Loop

Figure 6.4 Velocity versus time.

Proof. The proof is a direct consequence of Theorem 6.2 with

Q =

a+b

M, S =

M, R =

a+b

M, Q

= −

M, S

M, and

NonlinearBook10pt November 20, 2007

420 CHAPTER 6

0 1 2 3 4 5 6 7 8 9 10

−2.5

−2

−1.5

−1

−0.5

0.5

time

Control Effort

Figure 6.5 Control eﬀort versus time.

= −

M. Speciﬁcally, let σ > 0 be such that



(a + b)

−



> 0.

In this case,

Q given by (6.7) satisﬁes

Q =



(

a+b

−

σa

σ−1

M (

a+b

−



< 0,

so that all the conditions of Theorem 6.2 are satisﬁed.

6.3 Energy-Based Feedback Control

In this section, an energy-based control framework for port-controlled

Hamiltonian sys tems is established. Speciﬁcally, we develop a controller

design methodology that achieves stabilization via system passivation. In

particular, the interconnection and damping m atrix functions of the port-

controlled Hamiltonian system are shaped so th at the physical (Hamil-

tonian) sys tem structure is preserved at the closed-loop level and the

closed-loop energy function is equal to the diﬀerence between the physical

energy of the system and the energy su pplied by the controller. Since the

Hamiltonian structure is preserved at the closed-loop level, the passivity-

based controller is robust with respect to u nmodeled passive dynamics.

Furth ermore, passivity-based control architectures are extremely appealing

NonlinearBook10pt November 20, 2007

STABILITY OF FEEDBACK SYSTEMS 421

−1.5 −1 −0.5 0 0.5 1 1.5

−2

−1.5

−1

−0.5

0.5

1.5

Position

Velocity

Dynamic Feedback

Open−Loop

Figure 6.6 Phase portrait.

since the control action has a clear physical energy interpretation which can

considerably simplify controller implementation.

We begin by considering the port-controlled Hamiltonian system given

˙x(t) = [J(x(t)) − R(x(t))]



∂H

∂x

(x(t))



+ G(x(t))u(t),

x(0) = x

, t ≥ 0, (6.22)

y(t) = G

(x(t))



∂H

∂x

(x(t))



, (6.23)

where x(t) ∈ D ⊆ R

, D is an open set, u(t) ∈ U ⊆ R

, y(t) ∈ Y ⊆ R

H : D → R is a continuously diﬀerentiable Hamiltonian function for the

system (6.22) and (6.23), J : D → R

n×n

is such that J(x) = −J

(x),

R : D → S

is such that R(x) ≥ 0, x ∈ D, [J(x) − R(x)]



∂H

∂x

(x)



, x ∈ D,

is Lipschitz continuous on D, and G : D → R

n×m

. To address the energy-

based feedback control problem let φ : D → U. If u(t) = φ(x(t)), t ≥ 0, then

u(·) is a feedback control. Next, we pr ovide constructive suﬃcient conditions

NonlinearBook10pt November 20, 2007

422 CHAPTER 6

for energy-based feedback control of port-controlled Hamiltonian systems.

Speciﬁcally, we seek feedback controllers u(t) = φ(x(t)), t ≥ 0, where φ :

D → U, such that the closed-lo op system h as the form

˙x(t) = [J(x(t)) − R(x(t))]



∂H

∂x

(x(t))



+ G(x(t))φ(x(t))

= [J

(x(t)) − R

(x(t))]



∂H

∂x

(x(t))



, x(0) = x

, t ≥ 0, (6.24)

where H

: D → R is a shaped Hamiltonian function f or the closed-loop

system (6.24), J

: D → R

n×n

is a shaped interconnection matrix f unction

for the closed-loop system and satisﬁes J

(x) = −J

(x), and R

: D → S

a shaped dissipation matrix function f or the closed-loop system and satisﬁes

(x) ≥ 0, x ∈ D.

Theorem 6.3. Consider the nonlinear port-controlled Hamiltonian sy-

stem given by (6.22). Assume there exist functions φ : D → U, H

, H

: D →

R, J

, J

: D → R

n×n

, R

: D → R

n×n

such that H

(x) = H(x)+H

(x)

is continuously d iﬀerentiable, J

(x) = J(x) + J

(x), J

(x) = −J

(x),

(x) = R(x) + R

(x), R

(x) = R

(x) ≥ 0, x ∈ D, and

∂H

∂x

) = −

∂H

∂x

), x

∈ D, (6.25)

∂

∂x

) > −

∂

∂x

), x

∈ D, (6.26)

(x) − R

(x)]



∂H

∂x

(x)



= −[J

(x) − R

(x)]



∂H

∂x

(x)



+G(x)φ(x), x ∈ D. (6.27)

Then the equilibriu m solution x(t) ≡ x

of the closed-loop system (6.24) is

Lyapunov stable. If, in addition, D

⊆ D is a compact positively invariant

set with r espect to (6.24) and th e largest invariant set contained in R

△

{x ∈ D

∂H

∂x

(x)R

(x)



∂H

∂x

(x)



= 0} is M = {x

}, then the equilibrium

solution x(t) ≡ x

of the closed-loop system (6.24) is locally asymptotically

stable and D

is a subset of the domain of attraction of (6.24).

Proof. Cond ition (6.27) implies that w ith feedback controller u(t) =

φ(x(t)) the closed-loop system (6.22) has a Hamiltonian structure given

by (6.24). Fur thermore, it follows from (6.25) and (6.26) that the energy

function H

(·) has a local minimum at x = x

. Hence, x = x

is an

equilibrium point of the closed-loop system. Next, consider the Lyapunov

function candidate for the closed-loop system (6.24) given by V (x) =

(x) −H

). Now, the corresponding Lyapunov derivative of V (x) along

NonlinearBook10pt November 20, 2007

STABILITY OF FEEDBACK SYSTEMS 423

the closed-loop state trajectories x(t), t ≥ 0, is given by

V (x(t)) =

(x(t)) = −

∂H

∂x

(x(t))R

(x(t))



∂H

∂x

(x(t))



≤ 0, t ≥ 0.

(6.28)

Thus , it follows from Theorem 3.1 that the equilibr ium solution x(t) ≡ x

of (6.24) is L yapunov stable. Asymptotic stability of the closed-loop system

follows immediately from Corollary 3.1.

Theorem 6.3 presents constructive suﬃcient conditions for feedback

stabilization that preserve the physical Hamiltonian structure at the closed-

loop level while providing a shaped Hamiltonian energy function as a

Lyapunov function for the closed-loop system. These suﬃcient conditions

consist of a partial diﬀerential equation parameterized by the auxiliary

energy function H

, the auxiliary interconnection matrix f unction J

, and

auxiliary dissip ation matrix functions R

, and whose solution characterizes

the set of all desired sh aped energy functions that can be assigned while

preserving the system Hamiltonian structure at the closed-loop level. To

apply T heorem 6.3, we ﬁx the structur e of the interconnection J

(·) and

dissipation R

(·) matrix f unctions and solve for the closed-loop energy

function H

(·). Although in this case solving (6.27) appears formidable,

it is in fact quite tractable since the partial diﬀerential equation (6.27)

is parameterized via the interconnection and dissipation matrix functions

which can be chosen by the control designer to satisfy system physical

constraints. Alternatively, we can ﬁx the shaped Hamiltonian H

and solve

for the interconnection and dissipation matrix functions. In this case, we

do not need to solve a partial diﬀerential equation but rather an algebraic

equation.

If rank G(x) = m and rank[G(x) b(x)] = rank G(x) = m, where

b(x) = [J

(x) − R

(x)]



∂H

∂x

(x)



+ [J

(x) − R

(x)]



∂H

∂x

(x)



, (6.29)

then an explicit expression for the stabilizing feedback controller satisfying

(6.27) is given by φ(x) = (G

(x)G(x))

−1

(x)b(x), x ∈ D. Alternatively,

if ran k[G(x) b(x)] = rank G(x) < m, x ∈ D, then the feedback controller

φ(x) = G

†

(x)b(x)+[I

−G

†

(x)G(x)]z, x ∈ D, where (·)

†

denotes the Moore-

Penrose generalized inverse and z ∈ R

, satisﬁes (6.27).

Under certain conditions on the system dissipation, the energy-based

controller given by Theorem 6.3 provides an energy balance of the controlled

system. To see this, let R

(x) ≡ 0 and R(x)



∂H

∂x

(x)



= 0, x ∈ D. In this

NonlinearBook10pt November 20, 2007

424 CHAPTER 6

case, the closed-loop dynamics are given by

˙x(t) = [J

(x(t)) − R(x(t))]



∂H

∂x

(x(t))



, x(0) = x

, t ≥ 0. (6.30)

Along the trajectories x(t), t ≥ 0, it follows that

(x(t))

= −

∂H

∂x

(x(t))R(x(t))



∂H

∂x

(x(t))



= −



∂H

∂x

(x(t)) +

∂H

∂x

(x(t))



R(x(t))



∂H

∂x

(x(t)) +

∂H

∂x

(x(t))



= −

∂H

∂x

(x(t))R(x(t))



∂H

∂x

(x(t))



, t ≥ 0, (6.31)

or, equivalently using (5.67),

(x(t)) =

H(x(t)) −u

(t)y(t), t ≥ 0. (6.32)

Now, integrating (6.32) yields

(x(t)) = H(x(t)) −

(s)y(s)ds + κ, 0 ≤

t ≤ t, (6.33)

where κ

△

= H

(x(

t)) − H(x(

t)), which shows that the closed-loop energy

function H

(·) is equ al to the diﬀerence between the physical energy H(·) of

the system and the energy supplied by the controller modulo the constant

κ.

Example 6.3. Consider the inverted pen dulum shown in Figure 6.7,

where m = 1 kg and L = 1 m. The sys tem is governed by the dynamic

equation of motion

θ(t) −g sin θ(t) = u(t), θ(0) = θ

θ(0) =

, t ≥ 0, (6.34)

where g denotes the gravitational acceleration and u(·) is a (thruster) control

force. Deﬁning x

= θ and x

θ, we can rewrite the equation of motion

in state space form (6.22) with x

△

= [x

, x

]

J(x) =



0 1

−1 0



, R(x) = 0, G(x) =



−1



, (6.35)

D = R

, and Hamiltonian function H(·) corresponding to the total energy

in the system given by H(x) =

+ g cos x

Next, to stabilize the equilibrium point x

= [θ

, 0]

we assign the

shaped Hamiltonian H

(x) =

− θ

)

function for the closed-loop