Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach
Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007
STABILITY OF FEEDBACK SYSTEMS 425
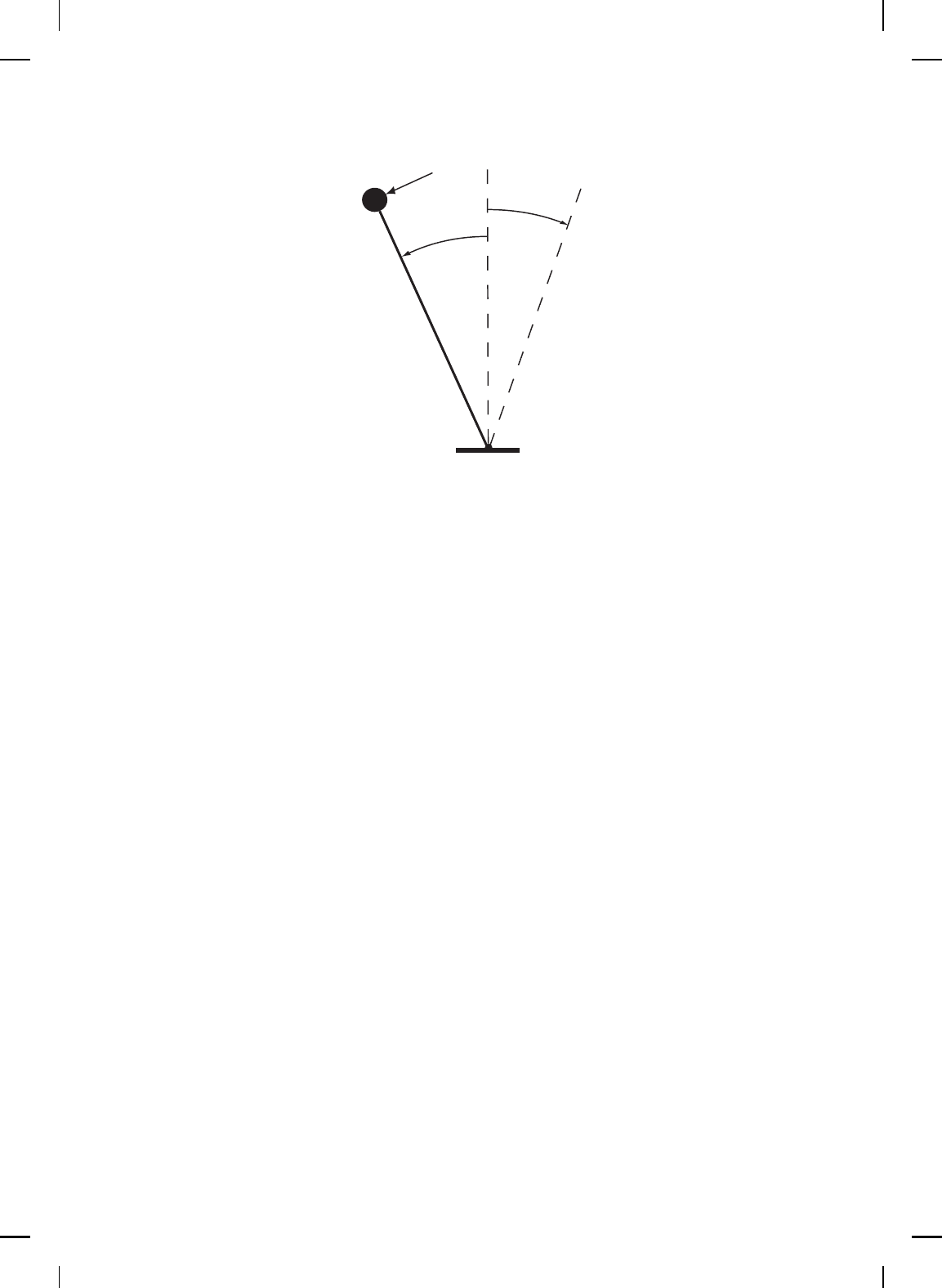
L
θ(t)
θ
e
m
u(t)
Figure 6.7 Inverted pendulum.
system. Furthermore, we set
J
a
(x) = 0, R
a
(x) =
0 0
0 1
, x ∈ D. (6.36)
In this case, it follows f rom (6.27) that the feedback controller is given by
u = φ(x) = x
2
+(x
1
−θ
e
)+g sin x
1
, x ∈ D. Next, note that
˙
H
s
(x) = −x
2
2
≤ 0,
x ∈ D. Hence, R
△
= {x ∈ D :
˙
H
s
= 0} = {x ∈ D : x
2
= 0}. Finally, since for
every x ∈ R, ˙x
2
6= 0 if and only x
1
6= θ
e
, it follows that the largest invariant
set contained in R is given by M = {x
e
}, and hence, the equilibrium solution
x(t) ≡ [θ
e
, 0]
T
is asymptotically stable. With θ
e
= 15
o
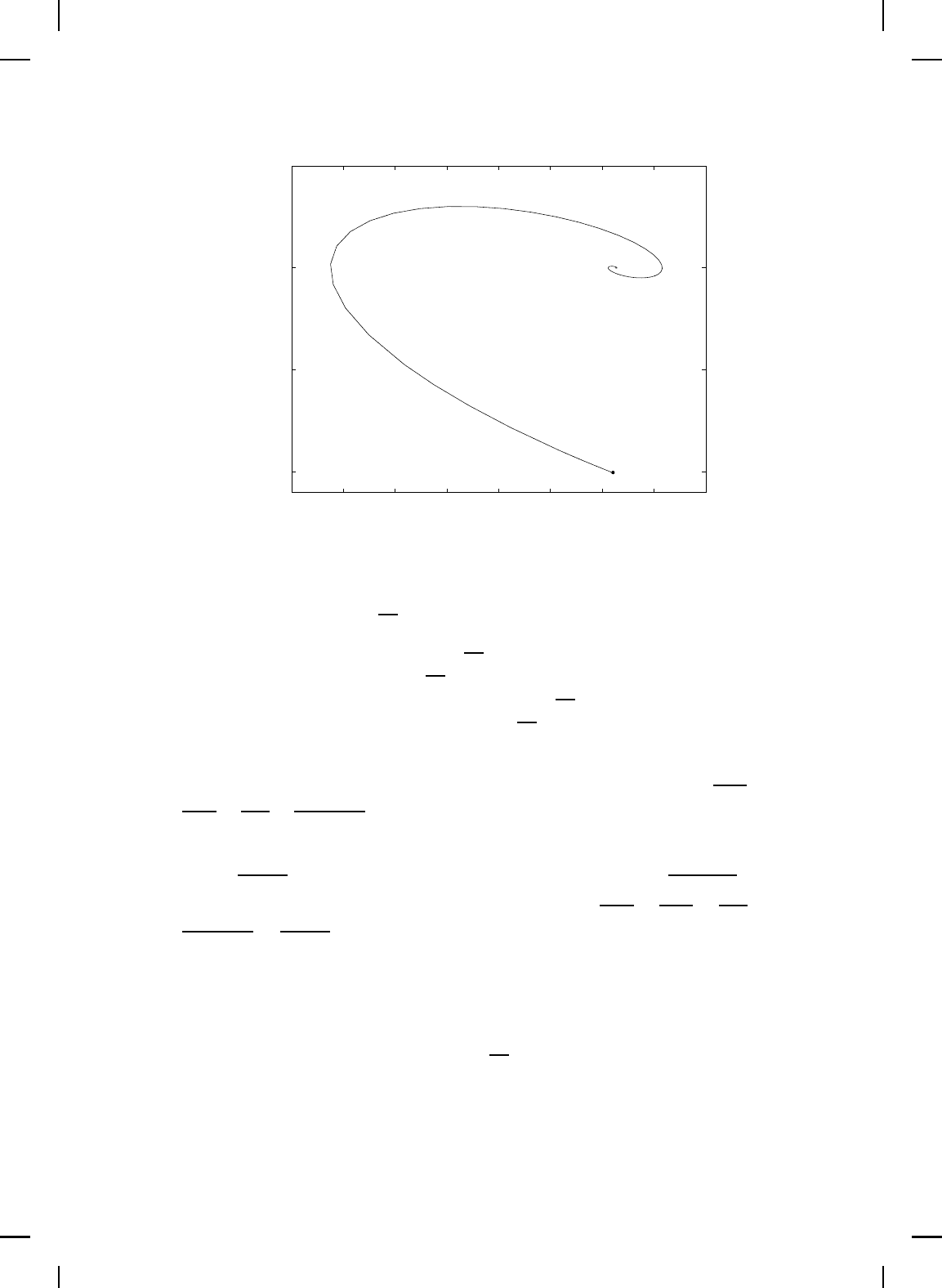
, Figure 6.8 shows the
phase portrait of the port-controlled Hamiltonian system. Figure 6.9 shows
the control force versus time and the shaped Hamiltonian versu s time. △
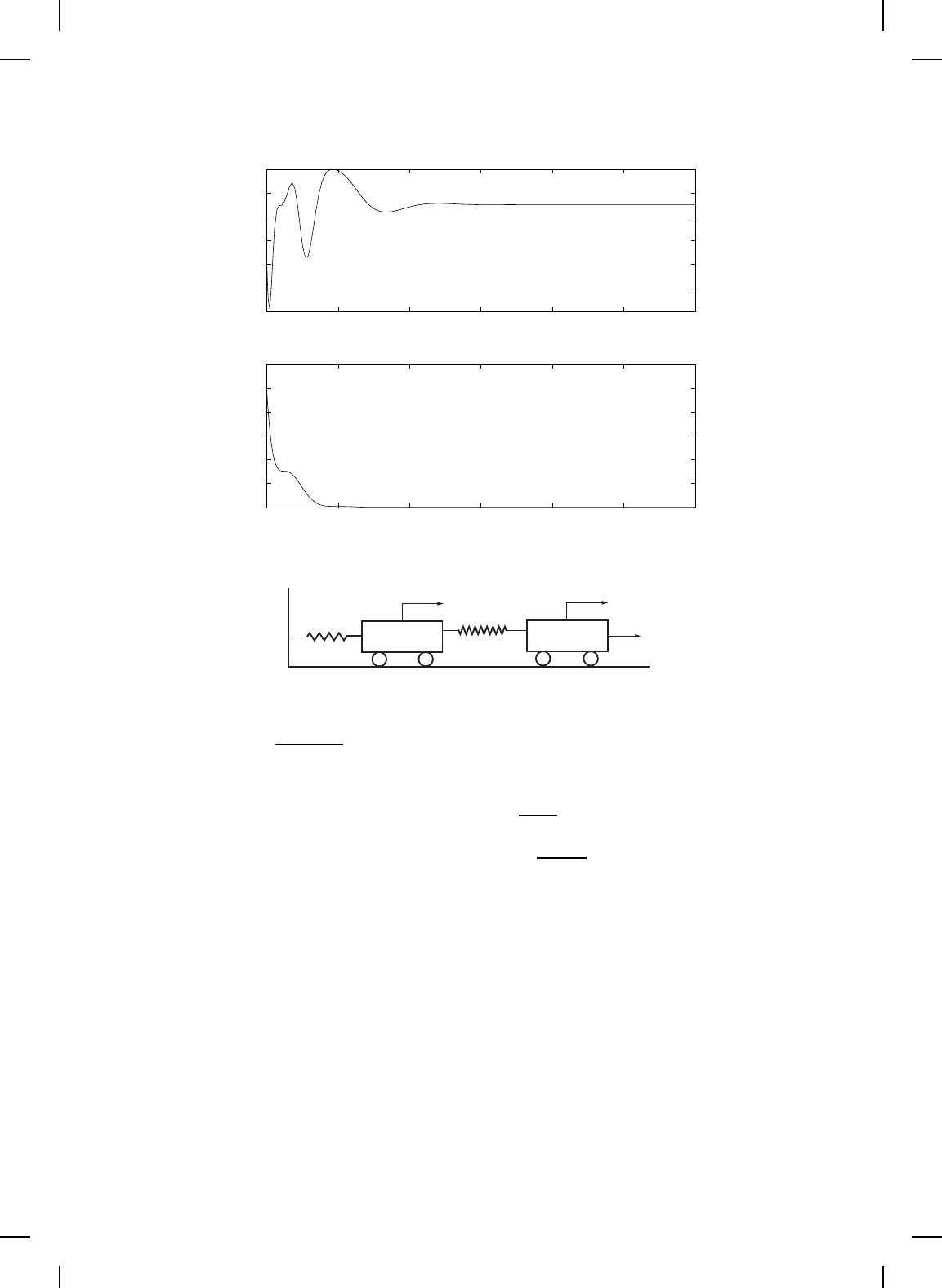
Example 6.4. Consider the two-mass, two-spring system shown in
Figure 6.10. A control force ˆu(·) acts on mass 2 with the goal to stabilize
the position of the second mass. The system dynamics, with state variables
defined in Figure 6.10, are given by
m
1
¨q
1
(t) + (k
1
+ k
2
)q
1
(t) − k
2
q
2
(t) = 0,
q
1
(0) = q
01
, ˙q
1
(0) = ˙q
01
, t ≥ 0, (6.37)
m
2
¨q
2
(t) −k
2
q
1
(t) + k
2
q
2
(t) = ˆu(t),
q
2
(0) = q
02
, ˙q
2
(0) = ˙q
02
. (6.38)
Defining x
1
= q
1
, x
2
= ˙q
1
, x
3
= q
2
, and x
4
= ˙q
2
, we can rewrite (6.37)
and (6.38) in state space form (6.22) with x = [x
1
, x
2
, x
3
, x
4
]
T
, R(x) = 0,
NonlinearBook10pt November 20, 2007
426 CHAPTER 6
-6 -5 -4 -3 -2 -1 0 1 2
-10
-5
0
5
θ(t)
˙
θ(t)
Figure 6.8 Phase portrait of the inverted pendulum.
G(x) = [0, 0, 0, 1]
T
, u =
ˆu
m
2
,
J(x) =
0
1
m
1
0 0
−
1
m
1
0 0 0
0 0 0
1
m
2
0 0 −
1
m
2
0
, (6.39)
D = {x ∈ R
4
: x
1
≥ 0, x
3
≥ 0}, and Hamiltonian function H(·)
corresponding to the total energy in the system given by H(x) =
m
1
x
2
2
2
+
m
2
x
2
4
2
+
k
1
x
2
1
2
+
k
2
(x
3
−x
1
)
2
2
.
Next, to stabilize the equilibrium point x
e
= [x
1e
, 0, x
3e
, 0]
T
, where
x
1e
=
k
2
(k
1
+k
2
)
x
3e
, w ith steady-state control value of u
c ss
=
k
1
k
2
m
2
(k
1
+k
2
)
x
3e
,
we assign the shaped Hamiltonian fun ction H
s
(x) =
m
1
x
2
2
2
+
m
2
x
2
4
2
+
k
1
x
2
1
2
+
k
2
(x
3
−x
1
)
2
2
−
k
1
k
2
(k
1
+k
2
)
x
3e
x
3
for the closed-loop system. Furthermore, we set
J
a
(x) ≡ 0 and
R
a
(x) =
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0
1
m
2
, x ∈ D. (6.40)
In this case, it follows f rom (6.27) that the feedback controller is given by
NonlinearBook10pt November 20, 2007
STABILITY OF FEEDBACK SYSTEMS 427
0 5 10 15 20 25 30
−20
−15
−10
−5
0
5
10
Time
Control force
0 5 10 15 20 25 30
0
10
20
30
40
50
60
Time
Shaped Hamiltonian
Figure 6.9 Control force and shaped Hamiltonian versus time.
m
1
m
2
k
1
k
2
q
1
(t) q
2
(t)
ˆu(t)
Figure 6.10 Two-mass, two-spring system.
u = φ(x) =
k
1
k
2
m
2
(k
1
+k
2
)
x
3e
− x
4
, x ∈ D. Next, note that
˙
H
s
(x) = −m
2
x
2
4
≤
0, x ∈ D. Hence, R
△
= {x ∈ D :
˙
H
s
= 0} = {x ∈ D : x
4
= 0}. Now, if
M ⊆ R is the largest invariant set contained in R, then f or every x
0
∈ M,
x
4
(t) ≡ 0, wh ich implies that x
1
(t)−x
3
(t)+
k
1
k
1
+k
2
x
3e
= 0 and ˙x
3
(t) = 0, t ≥
0. In this case, it follows that ˙x
1
(t) = 0, and hence, ˙x
2
(t) = 0, t ≥ 0. Hence,
the only point that belongs to M is x
e
= [
k
2
(k
1
+k
2
)
x
3e
, 0, x
3e
, 0]
T
, which
implies that x
e
is an asymptotically stable equilibrium point of the closed-
loop system. With m
1
= 1.5 kg, m
2
= 0.8 kg, k
1
= 0.1 N/m, k
2
= 0.3 N/m,
L = 0.4 m, and x
3e
= 3 m, Figure 6.11 shows the phase portrait of x
2
versus
x
4
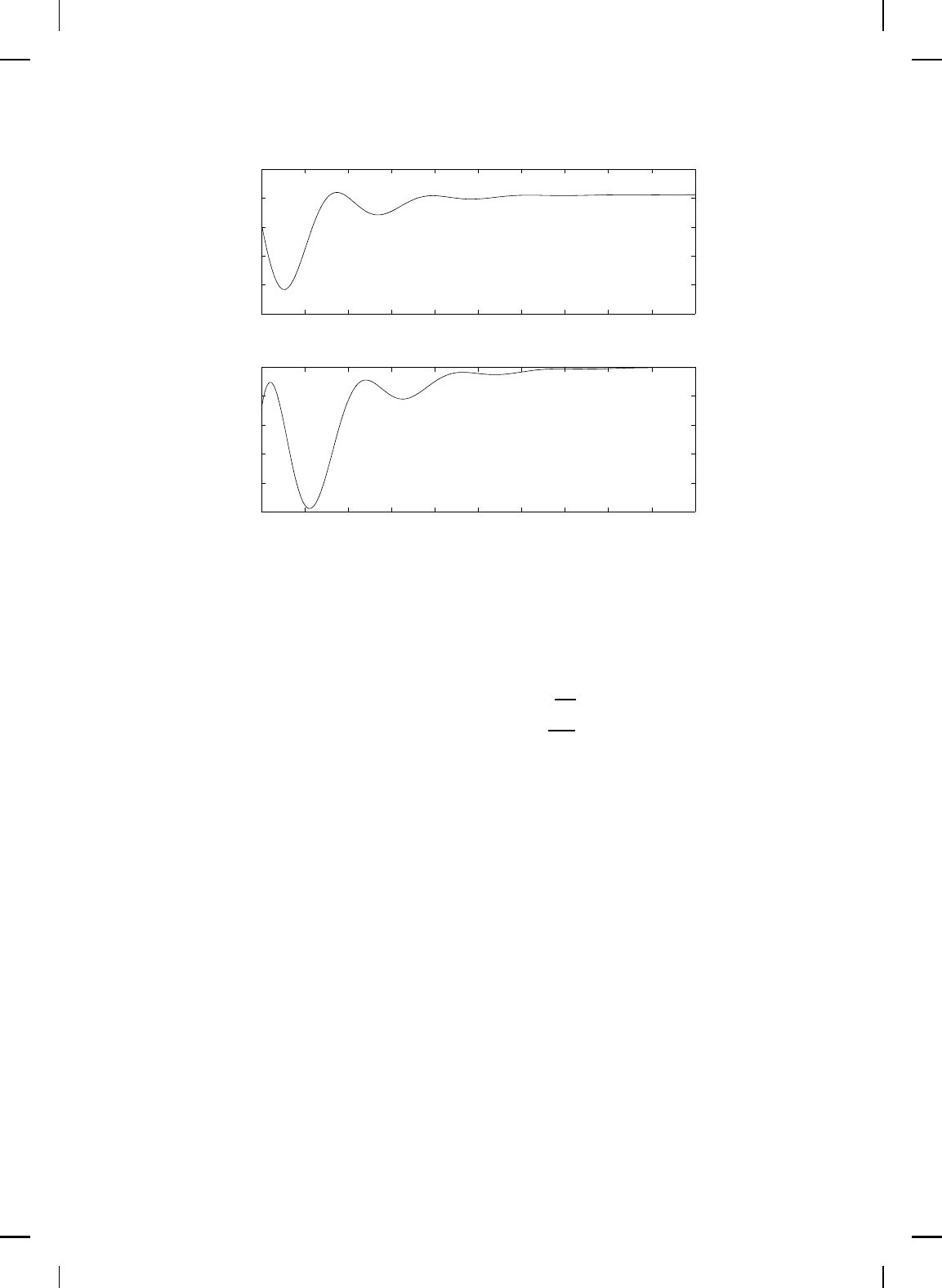
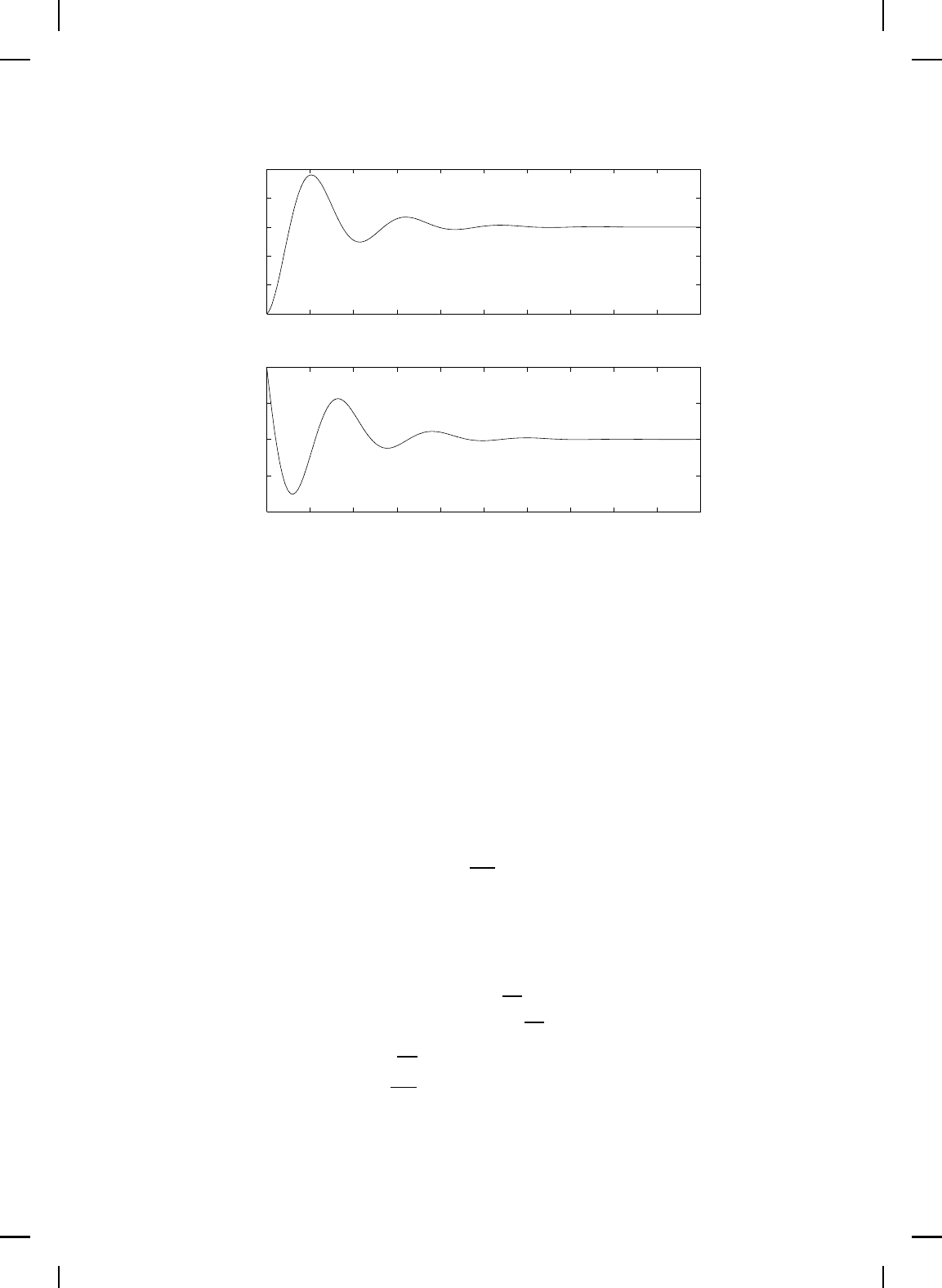
of the port-controlled Hamiltonian system. Figures 6.12 and 6.13 show,
respectively, the positions and velocities of the masses versus time. Finally,
Figure 6.14 sh ows the control force versus time and the shaped Hamiltonian
versus time. △
Next, we consider energy-based dynamic control for port-controlled
Hamiltonian systems wherein energy shaping is achieved by combining the
physical energy of the plant and the emulated energy of the controller.

NonlinearBook10pt November 20, 2007
428 CHAPTER 6
−3 −2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
Velocity of mass 1
Velocity of mass 2
Figure 6.11 Phase portrait of x
2
versus x
4
.
This approach has been extensively s tudied by Ortega et al. [340, 341] to
design Euler-Lagrange controllers for potential energy sh aping of m echanical
systems.
We begin by considering the port-controlled Hamiltonian system G
given by (6.22) and (6.23) with m = l. Fu rthermore, we consider the port-
controlled Hamiltonian feedback control system G
c
given by
˙x
c
(t) = [J
c
(x
c
(t)) − R
c
(x
c
(t))]
∂H
c
∂x
c
(x
c
(t))
T
+ G
c
(x
c
(t))u
c
(t),
x
c
(0) = x
c0
, t ≥ 0, (6.41)
y
c
(t) = G
T
c
(x
c
(t))
∂H
c
∂x
c
(x
c
(t))
T
, (6.42)
where x
c
(t) ∈ R
n
c
, u
c
(t) ∈ U
c
⊆ R
m
c
, y
c
(t) ∈ Y
c
⊆ R
l
c
, m
c
= l
c
, H
c
: R
n
c
→
R is a continuously differentiable Hamiltonian function of the feedback
control system G
c
, J
c
: R
n
c
→ R
n
c
×n
c
is such that J
c
(x
c
) = −J
T
c
(x
c
), R
c
:
R
n
c
→ S
n
c
is such that R
c
(x
c
) ≥ 0, x
c
∈ R
n
c
, [J
c
(x
c
) −R
c
(x
c
)]
∂H
c
∂x
c
(x
c
)
T
,
x
c
∈ R
n
c
, is Lipschitz continuous on R
n
c
, G
c
: R
n
c
→ R
n
c
×m
c
, m
c
= l, and
l
c
= m. Here, we assume that u
c
(·) is restricted to the class of admissible
inputs consisting of measurable functions su ch that u
c
(t) ∈ U
c
for all t ≥ 0.
Note that with the f eedback interconnection given by Figure 6.1, u
c
= y and
y
c
= −u. Hence, the closed-loop dynamics can be written in Hamiltonian
NonlinearBook10pt November 20, 2007
STABILITY OF FEEDBACK SYSTEMS 429
0 5 10 15 20 25 30 35 40 45 50
−6
−4
−2
0
2
4
Time
Position of mass 1
0 5 10 15 20 25 30 35 40 45 50
−2
−1
0
1
2
3
Time
Position of mass 2
Figure 6.12 Mass positions versus time.
form given by
˙
˜x(t) =
J(x(t)) −G(x(t))G
T
c
(x
c
(t))
G
c
(x
c
(t))G
T
(x(t)) J
c
(x
c
(t))
−
R(x(t)) 0
0 R
c
(x
c
(t))
∂H
∂x
(x(t))
T
∂H
c
∂x
c
(x
c
(t))
T
,
˜x(0) = ˜x
0
, t ≥ 0, (6.43)
where ˜x
△
= [x
T
, x
T
c
]
T
.
It can be seen f rom (6.43) that by relating the controller state
variables x
c
to the plant state variables x, one can shape the Hamiltonian
function H(·) + H
c
(·) so as to preserve the Hamiltonian structure under
dynamic feedback for part of the closed-loop system associated with
the plant dynamics. Since the closed-loop dynamical system (6.43) is
Hamiltonian involving skew-symmetric interconnection matrix function
terms and nonnegative-definite dissipation matrix function terms, we can
establish the existence of energy-Casimir functions [63,441] (i.e., dynamical
invariants) that are independent of the closed-loop Hamiltonian and relate
the controller states to the plant states. Since, as shown in Section 3.4,
energy-Casimir functions are comp osed of integrals of motion, it follows
that these functions are constant along the trajectories of the closed-loop
system (6.43). Fu rthermore, since the controller Hamiltonian H
c
(·) can
NonlinearBook10pt November 20, 2007
430 CHAPTER 6
0 5 10 15 20 25 30 35 40 45 50
−3
−2
−1
0
1
2
Time
Velocity of mass 1
0 5 10 15 20 25 30 35 40 45 50
−2
−1
0
1
2
Time
Velocity of mass 2
Figure 6.13 Mass velocities versus time.
be assigned, the en ergy-Casimir method can be used to construct suitable
Lyapunov functions for the closed-loop system.
To proceed, consider the candidate vector energy-Casimir fun ction E :
D×R
n
c
→ R
n
c
, where E(·, ·) is continuously differentiable and has the form
E(x, x
c
) = x
c
− F (x), (x, x
c
) ∈ D × R
n
c
, (6.44)
where F : D → R
n
c
is a continuously differentiable function. To ensure that
the candidate vector energy-Casimir fun ction E(·, ·) is constant along the
trajectories of (6.43) we require th at
˙
E(x(t), x
c
(t)) = ˙x
c
(t) −
∂F
∂x
(x(t)) ˙x(t) = 0, t ≥ 0. (6.45)
Now, we can arrive at a set of sufficient conditions which guarantee that
(6.45) holds. Specifically, it follows from (6.43) that (6.45) can be rewritten
as
˙
E(x(t), x
c
(t)) =
"
G
c
(x
c
)G
T
(x) −
∂F
∂x
(x)(J(x) − R(x))
T
J
c
(x
c
) −R
c
(x
c
) +
∂F
∂x
(x)G(x)G
T
c
(x
c
)
T
#
T
·
∂H
∂x
(x(t))
T
∂H
c
∂x
c
(x
c
(t))
T
. (6.46)

NonlinearBook10pt November 20, 2007
STABILITY OF FEEDBACK SYSTEMS 431
0 5 10 15 20 25 30 35 40 45 50
−2
−1
0
1
2
Time
Control signal
0 5 10 15 20 25 30 35 40 45 50
−2
0
2
4
6
8
10
Time
Shaped Hamiltonian
Figure 6.14 Control signal and shaped Hamiltonian versus time.
Hence, a set of sufficient conditions such that (6.45) holds is given by
G
c
(x
c
)G
T
(x) −
∂F
∂x
(x)(J(x) − R(x)) = 0, (x, x
c
) ∈ D × R
n
c
, (6.47)
J
c
(x
c
) −R
c
(x
c
) +
∂F
∂x
(x)G(x)G
T
c
(x
c
) = 0, (x, x
c
) ∈ D × R
n
c
. (6.48)
The following proposition su mmarizes the above results.
Proposition 6.1. Consider the feedback interconnection of the port-
controlled Hamiltonian systems G and G
c
given by (6.22) and (6.23), and
(6.41) and (6.42), respectively. If there exists a continuously differentiable
function F : D → R
n
c
such that for all (x, x
c
) ∈ D × R
n
c
,
∂F
∂x
(x)J(x)
∂F
∂x
(x)
T
− J
c
(x
c
) = 0, (6.49)
R
c
(x
c
) = 0, (6.50)
R(x)
∂F
∂x
(x)
T
= 0, (6.51)
∂F
∂x
(x)J(x) − G
c
(x
c
)G
T
(x) = 0, (6.52)
then
E(˜x(t)) = x
c
(t) − F (x(t)) = c, t ≥ 0, (6.53)
where c ∈ R
n
c
and ˜x(t) = [x
T
(t), x
T
c
(t)]
T
satisfies (6.43).
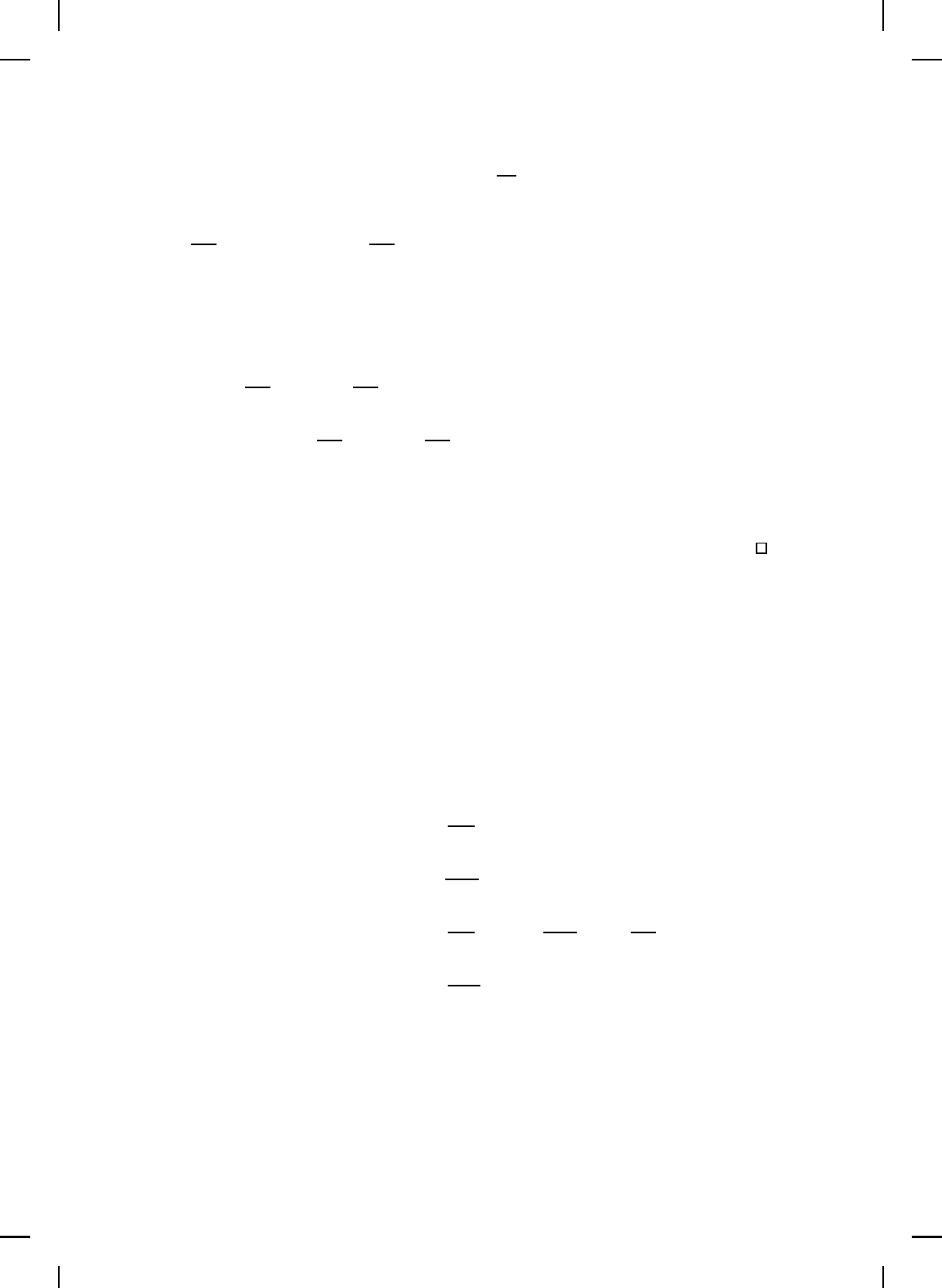
NonlinearBook10pt November 20, 2007
432 CHAPTER 6
Proof. Postmultiplying (6.47) by
∂F
∂x
(x)
T
, it follows from (6.47) and
(6.48) that
∂F
∂x
(x)[J(x) − R(x)]
∂F
∂x
(x)
T
= J
c
(x
c
) + R
c
(x
c
), (x, x
c
) ∈ D × R
n
c
.
(6.54)
Next, using the fact that the sum of a skew-symmetric and symmetric matrix
is zero if and only if the individual matrices are zero, it follows that (6.54)
is equivalent to
∂F
∂x
(x)J(x)
∂F
∂x
(x)
T
−J
c
(x
c
) = 0, (x, x
c
) ∈ D × R
n
c
, (6.55)
R
c
(x
c
) +
∂F
∂x
(x)R(x)
∂F
∂x
(x)
T
= 0, (x, x
c
) ∈ D × R
n
c
. (6.56)
Now, since R(x) ≥ 0, x ∈ D, and R
c
(x
c
) ≥ 0, x ∈ R
n
c
, it follows that (6.55)
and (6.56) are equivalent to (6.49)–(6.51). Hence, it follows that (6.47) can
be rewritten as (6.52). The equivalence between (6.47)–(6.48) and (6.49)–
(6.52) proves the result.
Note that conditions (6.49)–(6.52) are necessary and sufficient for
(6.47)–(6.48) to hold, which, in tu rn, provide sufficient conditions f or
guaranteeing that the vector energy-Casimir function E(·, ·) is constant
along the trajectories of the closed-loop system (6.43). The constant
vector c ∈ R
n
c
in (6.53) depends on the in itial conditions for the plant
and controller states. If conditions (6.49)–(6.52) are satisfied, then the
controller state variables along the trajectories of the closed-loop system
given by (6.43) can be represented in terms of the plant s tate variables as
x
c
(t) = F (x(t)) + c, t ≥ 0, x(t) ∈ D, c ∈ R
n
c
. In this case, it follows that
the closed-loop system associated with the plant dynamics is given by
˙x(t) = [J(x(t)) − R(x(t))]
∂H
∂x
(x(t))
T
−G(x(t))G
T
c
(x
c
(t))
∂H
c
∂x
c
(x
c
(t))
T
= [J(x(t)) − R(x(t))]
∂H
∂x
(x(t)) +
∂H
c
∂x
c
(x
c
(t))
∂F
∂x
(x(t))
T
= [J(x(t)) − R(x(t))]
∂H
s
∂x
(x(t))
T
, x(0) = x
0
, t ≥ 0, (6.57)
where H
s
(x) = H(x) + H
c
(F (x) + c), x ∈ D, is the shaped Hamiltonian
function for the closed-loop system (6.57).
Next, we use the existence of the vector energy-Casimir function to
NonlinearBook10pt November 20, 2007
STABILITY OF FEEDBACK SYSTEMS 433
construct stabilizing dynamic controllers that guarantee that the closed-
loop system associated with the plant dynamics preserves the Hamiltonian
structure without the need for solving a set of partial d ifferential equations.
Theorem 6.4. Consider the feedback interconnection of the port-
cont-rolled Hamiltonian systems G and G
c
given by (6.22) and (6.23), and
(6.41) and (6.42), respectively. Assume that there exists a continuously
differentiable function F : D → R
n
c
such that conditions (6.49)–(6.52)
hold for all (x, x
c
) ∈ D × R
n
c
, and assume that the Hamiltonian fu nction
H
c
: R
n
c
→ R of the feedback controller G
c
is such that H
s
: D → R is given
by H
s
(x) = H(x) + H
c
(F (x) + c), x ∈ D. If
∂H
c
∂x
(F (x
e
) + c) = −
∂H
∂x
(x
e
), x
e
∈ D, (6.58)
∂
2
H
c
∂x
2
(F (x
e
) + c) > −
∂
2
H
∂x
2
(x
e
), x
e
∈ D, (6.59)
then the equilibrium solution x(t) ≡ x
e
of the system (6.57) is Lyapunov
stable. If, in addition, D
c
⊆ D is a compact positively invariant set with
respect to (6.57) and the largest invariant set contained in R
△
= {x ∈ D
c
:
∂H
s
∂x
(x)R(x)
∂H
s
∂x
(x)
T
= 0} is M = {x
e
}, then the equilibrium solution
x(t) ≡ x
e
of the closed-loop system (6.57) is locally asymptotically stable.
Proof. Conditions (6.49)–(6.52) imply that the closed-loop dynamics
of the port-controlled Hamiltonian system G and th e controller G
c
associated
with the plant states can be written in the form given by (6.57). Now,
using identical arguments as in the proof of Theorem 6.3, conditions (6.58)
and (6.59) guarantee the existence of the Lyapunov function candidate
V (x) = H
s
(x) − H
s
(x
e
), x ∈ D, which guarantees Lyapunov stability of the
equilibrium solution x(t) ≡ x
e
of the closed-loop system (6.57). Asymptotic
stability of x(t) ≡ x
e
follows from Corollary 3.1.
As in the static controller case, the dynamic controller given by
Theorem 6.4 also provides an energy balance interpretation over the
trajectories of the controlled system. To see this, note th at since by (6.50),
R
c
(x
c
) = 0, x
c
∈ R
n
c
, it follows that th e controller Hamiltonian H
c
(·)
satisfies
˙
H
c
(F (x(t)) + c) = y
T
c
(t)y(t) = −u
T
(t)y(t), t ≥ 0. (6.60)
Now, it follows that
˙
H
s
(x(t)) =
˙
H(x(t)) +
˙
H
c
(F (x(t)) + c)
=
˙
H(x(t)) −u
T
(t)y(t), t ≥ 0, (6.61)
which yields (6.33).
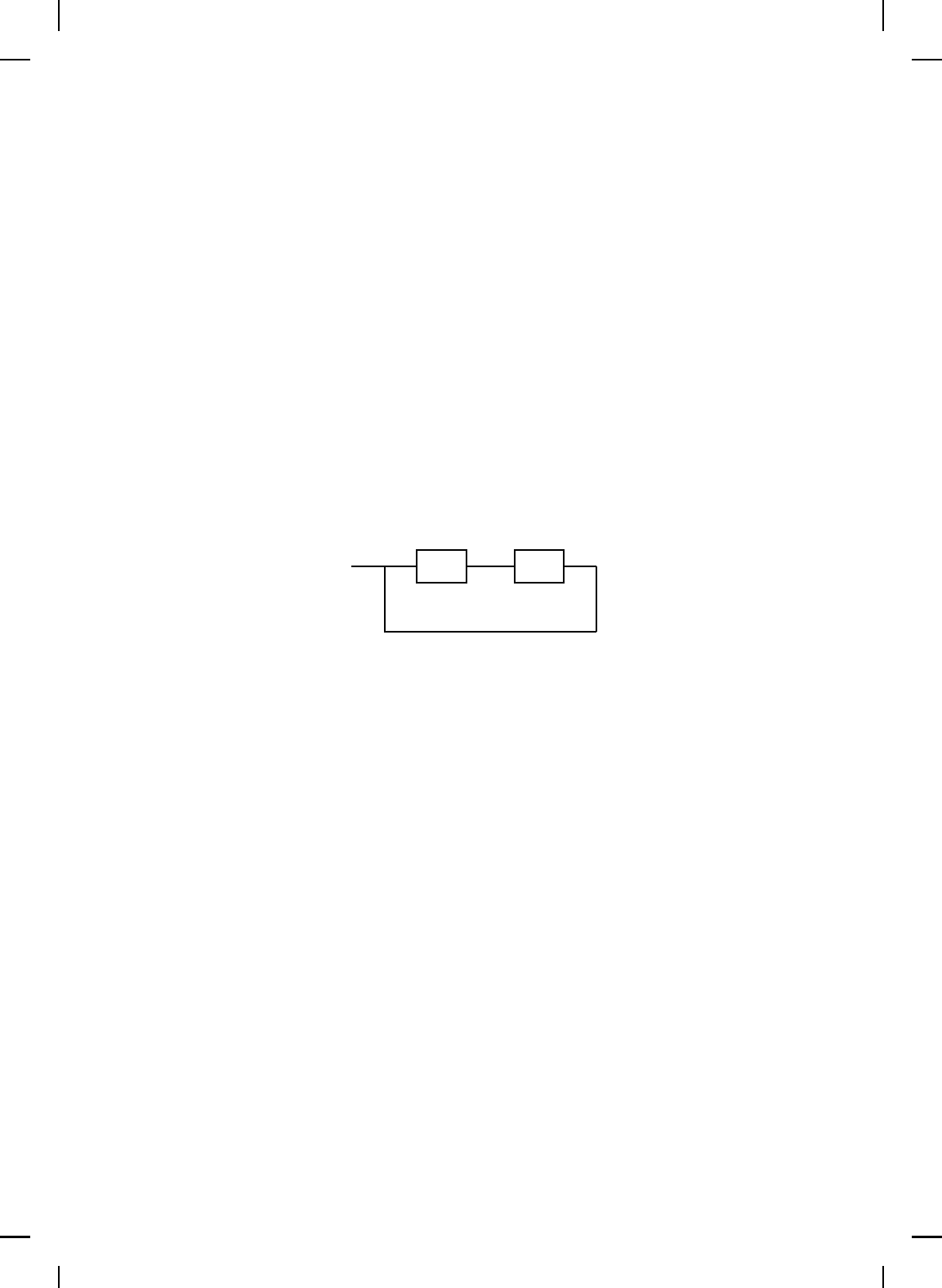
NonlinearBook10pt November 20, 2007
434 CHAPTER 6
6.4 Stability Margins for Nonlinear Feedback Regulators
To develop relative s tability margins for nonlinear regulators consider th e
nonlinear dynamical system G given by
˙x(t) = f (x(t)) + G(x(t))u(t), x(0) = x
0
, t ≥ 0, (6.62)
y(t) = −φ(x(t)), (6.63)
where φ : R
n
→ R
m
is such that G is asymptotically stable with u = −y.
Furth ermore, assume that the system G is zero-state observable. Next,
we define the relative stability margins for G given by (6.62) and (6.63).
Specifically, let u
c
△
= −y, y
c
△
= u, and consider the negative f eedback
interconnection u = ∆(−y) of G and ∆(·) given in Figure 6.15, where
∆(·) is either a linear operator ∆(u
c
) = ∆u
c
, a nonlinear static operator
∆(u
c
) = σ(u
c
), or a dynamic nonlinear operator ∆(·) with input u
c
and
output y
c
. Furth ermore, we assume that in the nominal case ∆(·) = I(·) so
that the nominal closed-loop system is asymptotically stable.
∆(·)
G
- -
−
Figure 6.15 Multiplicative input uncertainty of G and input operator ∆(·).
Definition 6.1. Let α, β ∈ R be such that 0 < α ≤ 1 ≤ β < ∞.
Then the nonlinear d ynamical system G given by (6.62) an d (6.63) is said to
have a gain margin (α, β) if the negative feedback interconnection of G and
∆(u
c
) = ∆u
c
is globally asymptotically stable for all ∆ = diag[k
1
, . . . , k
m
],
where k
i
∈ (α, β), i = 1, . . . , m.
Definition 6.2. Let α, β ∈ R be such that 0 < α ≤ 1 ≤ β < ∞.
Then the nonlinear dynamical system G given by (6.62) and (6.63) is said
to have a sector margin (α, β) if the negative feedback interconnection of
G and ∆(u
c
) = σ(u
c
) is globally asymptotically stable for all nonlinearities
σ : R
m
→ R
m
such that σ(0) = 0, σ(u
c
) = [σ
1
(u
c1
), . . . , σ
m
(u
cm
)]
T
, and
αu
2
ci
< σ
i
(u
ci
)u
ci
< βu
2
ci
, f or all u
ci
6= 0, i = 1, . . . , m.
Definition 6.3. Let α, β ∈ R be such that 0 < α ≤ 1 ≤ β < ∞. Then
the nonlinear dynamical system G given by (6.62) and (6.63) is said to have
a disk marg in (α, β) if the negative feedback interconnection of G and ∆(·)
is globally asymptotically stable for all dynamic operators ∆(·) such that
∆(·) is zero-state observable and dissipative with respect to the supply rate
