Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 375

F ∈ [M

, M

], is asymp totically stable, then the zero solution x(t) ≡ 0 to

(5.195)–(5.197) is globally asymptotically stable for all σ : R → R such that

≤ σ

′

(y) ≤ M

Note that since σ : R → R in Kalman’s conjecture is such that

≤ σ

′

(y) ≤ M

, it follows from the mean value th eorem that σ(·) ∈

Φ. T he converse, of course, is not necessarily true. Hence, Kalman’s

conjecture considers a reﬁned class of feedback nonlinearities as compared

to Aizerman’s conjecture. Nevertheless, Kalman’s conjecture is also false.

However, it is important to note that if the zero solution x(t) ≡ 0 to (5.195)–

(5.197) with σ(y) = F y, where F ∈ [M

, M

], is asymptotically stable, then

the zero solution x(t) ≡ 0 to (5.195)–(5.197) is locally asymptotically stable

for all σ : R → R such that M

≤ σ

′

(y) ≤ M

. This follows as a direct

consequence of Lyapunov’s indirect method.

5.8 The Positivity Theorem and the Circle Criterion

In this section, we present suﬃcient conditions for an absolute stability

problem involving a dynamical system with memoryless, time-varyin g

feedback nonlinearities. In the case where m = l = 1, these suﬃcient

conditions involve inclusion/exclusion of the Nyquist plot of (5.195) and

(5.197) in/from a disk region that encomp asses the critical point, and

hence, ensures stability. Appropriately, this result is known as the circle

criterion or circle theorem. First, we present the simplest version of the circle

criterion known as the positivity theorem involving a half-plane exclusion

of the Nyqu ist plot of (5.195) and (5.196). For this result we assume that

σ(·, ·) ∈ Φ

, where

△

= {σ : R

× R

→ R

: σ(0, ·) = 0, σ

(y, t)[σ(y, t) − M y] ≤ 0, y ∈ R

a.e. t ≥ 0, and σ(y, ·) is Lebesgue measurable for all y ∈ R

(5.200)

where M ∈ R

m×l

Theorem 5.18 (Positivity Theorem). Consider the nonlinear dynam-

ical system (5.195)–(5.197). Suppose

G(s) ∼



A B

C D



is minimal and I

+ MG(s) is strictly positive real. Then the zero solution

x(t) ≡ 0 of the negative feedback interconnection of (5.195)–(5.197) is

globally exponentially stable for all σ(·, ·) ∈ Φ

NonlinearBook10pt November 20, 2007

376 CHAPTER 5

Proof. First note that the negative feedback interconnection of

(5.195)–(5.197) has the state space representation

˙x(t) = Ax(t) − Bσ(y(t), t), x(0) = x

, t ≥ 0, (5.201)

y(t) = Cx(t) − Dσ(y(t), t). (5.202)

Now, it follows from Theorem 5.14 that since I

+MG(s) is str ictly positive

real and minimal, there exist matrices P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

with P positive deﬁnite, and a scalar ε > 0 such that

0 = A

P + P A + εP + L

L, (5.203)

0 = B

P − MC + W

L, (5.204)

0 = (I + MD) + (I + MD)

− W

W. (5.205)

Next, consider the Lyapunov fu nction candidate V (x) = x

P x, where

P satisﬁes (5.203)–(5.205). The corresponding Lyapunov derivative is given

V (x) = V

′

(x)[Ax − Bσ(y, t)]

= 2x

P [Ax −Bσ(y, t)]

= x

P + P A)x − 2σ

(y, t)B

P x

= −x

(εP + L

L)x − σ

(y, t)B

P x − x

P Bσ(y, t). (5.206)

Now, adding and subtracting 2σ

(y, t)(I

+ M D)σ(y, t) and 2σ

(y, t)MCx

to and from (5.206) yields

V (x) = −εx

P x − x

Lx − σ

(y, t)(B

P − MC)x − x

P − MC)

·σ(y, t) − σ

(y, t)[(I

+ M D) + (I

+ M D)

]σ(y, t) + 2σ

(y, t)

·[σ(y, t) − M(Cx −Dσ(y, t))], (5.207)

or, equivalently,

V (x) = −εx

P x − [Lx − W σ(y, t)]

[Lx − W σ(y, t)]

+2σ

(y, t)[σ(y, t) − M y]. (5.208)

Since σ

(y, t)[σ(y, t) − M y] ≤ 0 for all t ≥ 0 and σ(·, ·) ∈ Φ

, it

follows that

V (x) ≤ −εV (x), x ∈ R

, which shows that the zero solution

x(t) ≡ 0 of the negative f eedback interconnection of (5.195)–(5.197) is

globally exponentially stable for all σ(·, ·) ∈ Φ

In the single-input, single-output case, the frequency domain condition

in Theorem 5.18 has an interesting geometric interpr etation in the Nyquist

plane. Speciﬁcally, setting G(ω) = x + y and requiring that 1 + MG(s) be

strictly positive real if follows that

x = Re G(ω) > −

, ω ∈ R, (5.209)

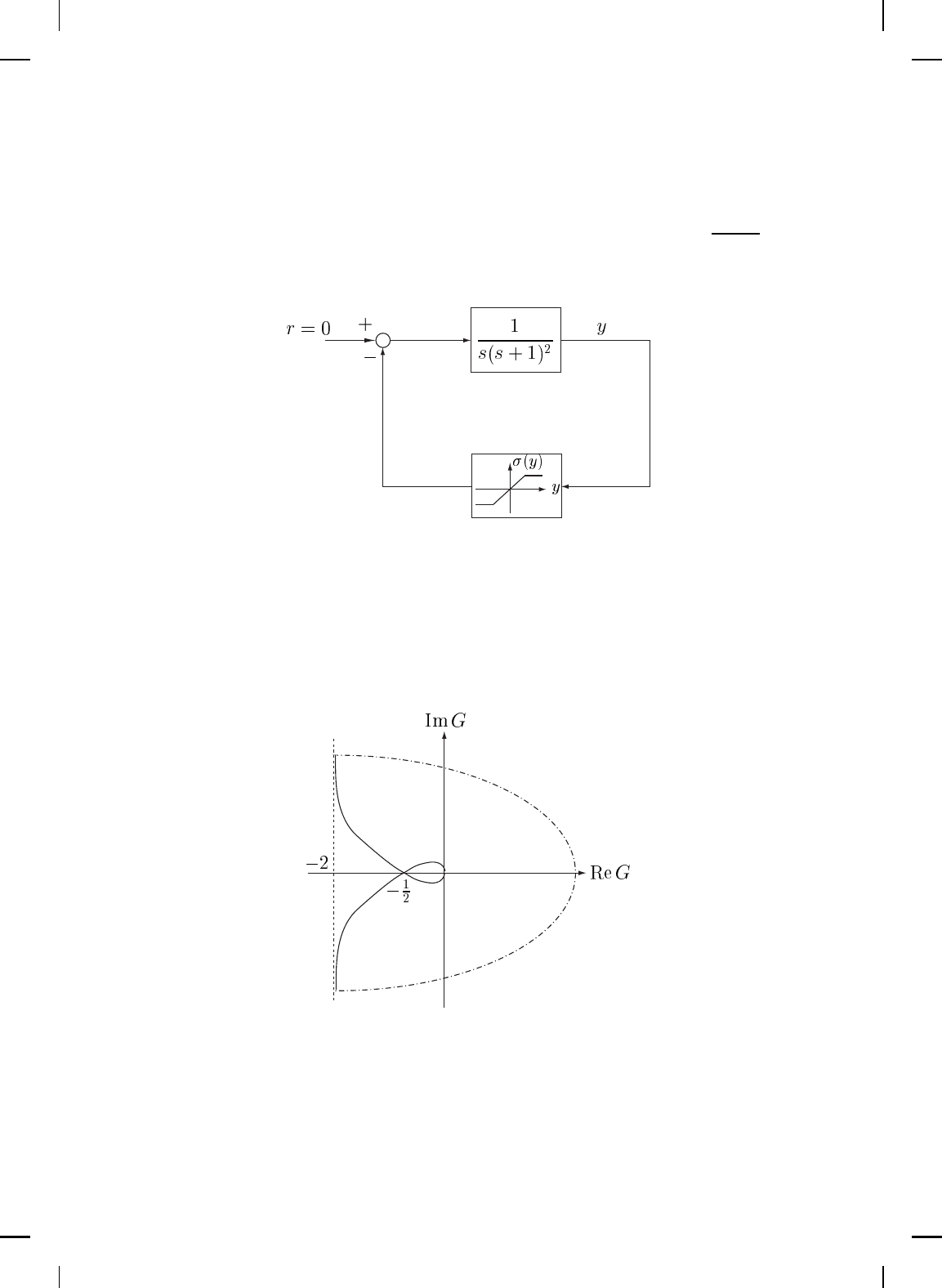
NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 377

which is equivalent to the graphical condition that the Nyquist p lot of G(ω)

lies to the right of the vertical line deﬁned by Re[s] = −1/M.

Example 5.7. Consider the linear dynamical system G(s) =

s(s+1)

with a saturation feedback nonlinearity belonging to the sector [0, M] shown

in Figure 5.3. Note that lim

ω →0

|G(ω)| = ∞, lim

ω →0

∠G(ω) = −90

◦

Figure 5.3 Feedback connection with saturation nonlinearity.

lim

ω →∞

|G(ω)| = 0, and lim

ω →∞

∠G(ω) = −270

◦

. Furthermore, the real

axis crossing of the Nyquist plot of G(ω) corresponds to ω = 1 rad/sec, and

hence, Re[G(ω)]|

ω = 1

= −1/2. Also note that Re[G(ω)]|

ω = 0

= − 2. Hence,

the Nyquist plot of G(ω) lies to the right of the vertical line Re[s] = −2 (see

Figure 5.4). Thus , it follows from the positivity theorem that the system is

globally exponentially stable for all nonlinearities in the sector [0, 0.5]. △

Figure 5.4 Nyquist plot for Example 5.7.

The positivity theorem applies to the case where the time-varying

feedback nonlinearity belongs to the sector Φ

. Since in this case σ(y, t) ≡ 0

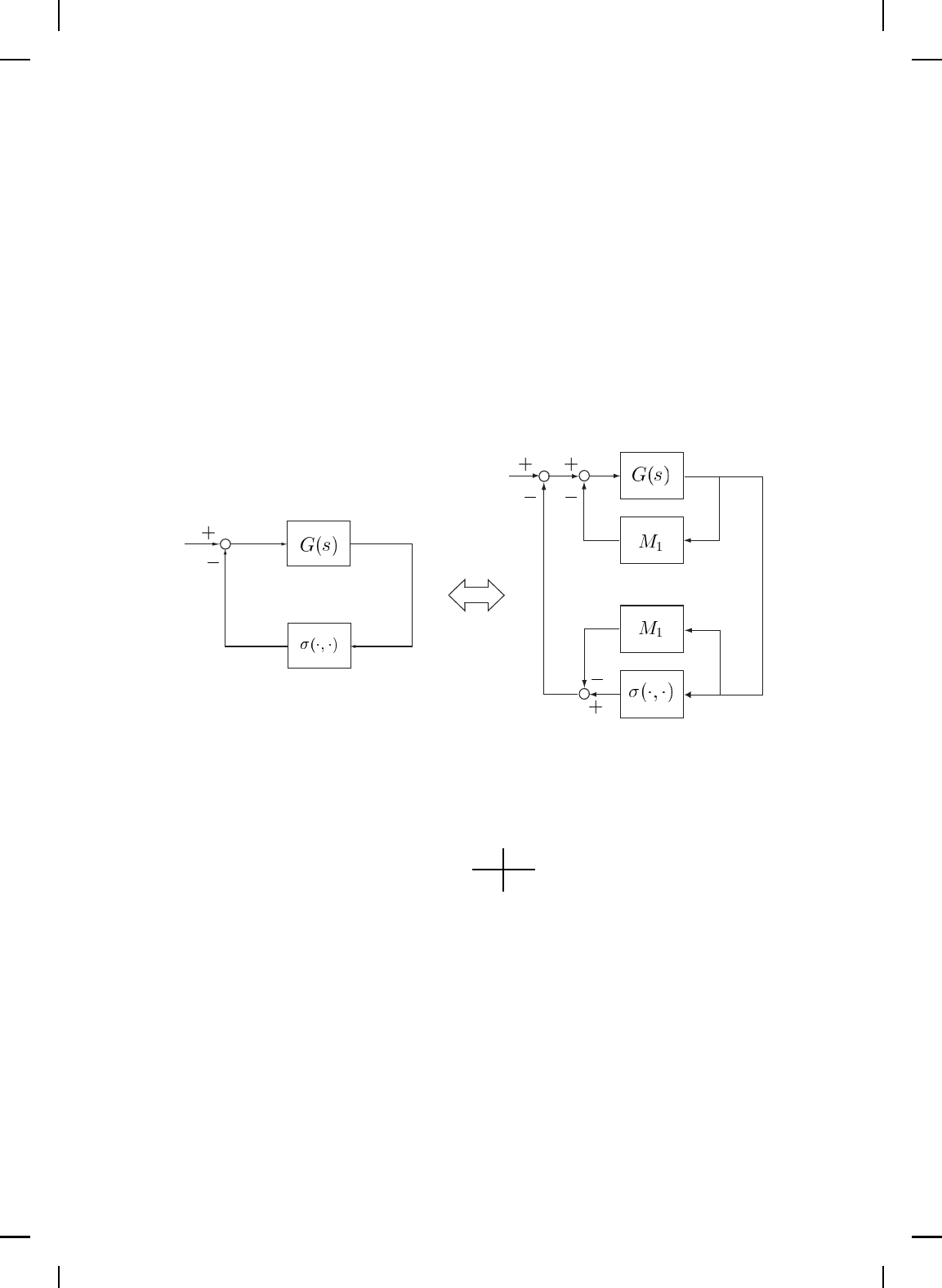
NonlinearBook10pt November 20, 2007

378 CHAPTER 5

is an admissible feedback nonlinearity, it is clear that a necessary condition

for guaranteeing absolute stability is that A be Hurwitz. Next, using loop

shifting techn iques, we consider the more general case where the feedback

nonlinearity belongs to the general s ector Φ. In this case, the r estriction on

A being Hurw itz can be removed. To consider double sector nonlinearities

characterized by Φ note that if σ(·, ·) ∈ Φ , then the shifted nonlinearity

(y, t)

△

= σ(y, t) − M

(y) belongs to Φ

with M

△

= M

− M

. Hence,

transforming the forward path from G(s) to G

(s)

△

= (I + G(s)M

)

−1

G(s)

with feedback nonlinearity σ

(·, ·) ∈ Φ

gives an equ ivalent r ep resentation

to the dynamical system G(s) with feedback nonlinearity σ(·, ·) ∈ Φ. This

equivalence is shown in Figure 5.5. Thus , the following result is a dir ect

consequence of Theorem 5.18.

Figure 5.5 Equivalence via loop shifting.

Corollary 5.8 (Circle Theorem). Consider the non linear dynamical

system (5.195)–(5.197). Suppose

G(s) ∼



A B

C D



is minimal, det[I

+ M

G(s)] 6= 0, Re[s] ≥ 0, and [I

+ M

G(s)][I

G(s)]

−1

is strictly positive real. T hen, the zero solution x(t) ≡ 0

of the negative feedback interconnection of (5.195)–(5.197) is globally

exponentially stable for all σ(·, ·) ∈ Φ.

Proof. It need only be shown that the transformed system satisﬁes

the hypotheses of Theorem 5.18. First, it follows from simple algebraic

manipulations th at [I + M

G(s)][I + M

G(s)]

−1

= I + (M

− M

)(I +

G(s)M

)

−1

G(s) = I +MG

(s). Hence, by assumption, I +MG

(s) is strictly

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 379

positive real. In addition, the realization of I + MG

(s) is given by

I + MG

(s) ∼



A − B(I + M

−1

C B(I + M

−1

M(I + DM

)

−1

C I + M(I + DM

)

−1



(5.210)

which is minimal if (A, B, C) is minimal. Hence, all the conditions of

Theorem 5.18 are satisﬁed for the transf ormed system G

(s) with feedback

nonlinearities σ

(·, ·) ∈ Φ

Corollary 5.8 is known as the multivariable circle theorem or circle

criterion. Note that in the case where M

= 0, Corollary 5.8 specializes to

Theorem 5.18. Alternatively, in the case where M

= −γ

−1

I and M

−1

I, where γ > 0, Corollary 5.8 reduces to the classical small gain theorem

which states that if G is gain bounded, that is, |||G(s)|||

∞

< γ, then the

zero solution of the feedback interconnection of G with a gain bounded

nonlinearity kσ(y, t)k

≤ γ

−1

kyk

, y ∈ R

, almost everywhere t ≥ 0, is

uniformly asymptotically stable. To see this, ﬁrst note that in the case

where M

= −γ

−1

I and M

= γ

−1

I, Φ specializes to

△

= {σ : R

× R

→ R

: σ(0, ·) = 0, kσ(y, t)k

≤ γ

−1

kyk

, y ∈ R

a.e. t ≥ 0, and σ(y, ·) is Lebesgue measurable for all y ∈ R

(5.211)

Furth ermore, the strict positive real condition in Corollary 5.8 implies

[I + γ

−1

G(ω)][I − γ

−1

G(ω)]

−1

+ [I − γ

−1

∗

(ω)]

−1

[I + γ

−1

∗

(ω)] > 0,

ω ∈ R, (5.212)

or, equivalently, forming [I − γ

−1

∗

(ω)](5.212)[I − γ

−1

G(ω)] yields

∗

(ω)G(ω) < γ

I, ω ∈ R,

1/2

max

∗

(ω)G(ω)] < γ, ω ∈ R,

max

[G(ω)] < γ, ω ∈ R,

sup

ω ∈R

max

[G(ω)] < γ,

|||G(s)|||

∞

< γ. (5.213)

In the scalar case, the circle criterion provides a very interesting and

elegant graphical interpretation in terms of an in clusion/exclusion of the

Nyquist plot of G(s) in/from a disk region in the Nyquist plane. To arrive

at this result, let M

6= 0, M

6= 0, and M

< M

, and n ote that setting

G(ω) = x + y, the strict positive real condition in Corollary 5.8 implies

that



G(ω)

1 + M

G(ω)



− M

> 0, ω ∈ R, (5.214)

NonlinearBook10pt November 20, 2007

380 CHAPTER 5

or, equivalently,

(1 + M

x)(1 + M

x) + M

(1 + M

+ M

> 0, ω ∈ R. (5.215)

Next, suppose A in the realization of G(s) has ν eigenvalues with

positive real parts. Then, it follows from the Nyquist criterion [445] that

(s) is asymptotically stable if and only if the number of counterclockwise

encirclements of the −1/M

+0 point of the image of the clockwise Nyquist

contour Γ under the mapping G(s) equals the number of unstable poles of

the loop gain transfer f unction M

G(s). Hence, it follows from Corollary

5.8 that the zero solution x(t) ≡ 0 of the negative feedback interconnection

of (5.195)–(5.197) is globally exponentially stable f or all σ(·, ·) ∈ Φ if th e

Nyquist plot of G(s) does not intersect the point −1/M

+ 0 and encircles

it ν times counterclockwise, and (5.214) holds. However, (5.214) holds if

and only if

(x + 1/M

)(x + 1/M

) + y

> 0, ω ∈ R, (5.216)

for M

> 0, and if and only if

(x + 1/M

)(x + 1/M

) + y

< 0, ω ∈ R, (5.217)

for M

< 0. Hence, (5.214) holds if and only if for all ω ∈ R, G(ω)

lies outside the disk D(M

, M

) centered at (M

+ M

)/(2M

+ 0) with

radius (M

− M

)/2|M

| in the case where M

> 0, and lies in the

interior of the disk D(M

, M

) in the case where M

< 0. In the former

case, if the Nyquist plot does not enter the disk D(M

, M

) and encircles

the point −1/M

+ 0 ν times counterclockwise, then th e Nyquist plot must

encircle the disk D(M

, M

) ν times and vice versa. In light of the above

the following theorem is immediate.

Theorem 5.19 (Circle Crit erion). Consider the nonlinear dynamical

system (5.195)–(5.197) with m = l = 1 and σ(·, ·) ∈ Φ. Furth ermore,

suppose A has ν eigenvalues with positive real parts. Then, the zero

solution x(t) ≡ 0 of the negative feedback interconnection of (5.195)–(5.197)

is globally exponentially stable for all σ(·, ·) ∈ Φ if one of the following

conditions is satisﬁed, as appropriate:

i) I f 0 < M

< M

, the Nyquist plot of G(ω) d oes not enter the disk

D(M

, M

) and encircles it ν times counterclockwise.

ii) If 0 = M

< M

, A is Hurwitz, and the Nyquist plot of G(ω) lies in

the half plane {s ∈ C : Re[s] > −1/M

iii) If M

< 0 < M

, A is Hurwitz, and the Nyquist plot of G(ω) lies in

the interior of the disk D(M

, M

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 381

iv) If M

< M

≤ 0, replace G(·) by −G(·), M

by −M

, M

by −M

and apply i) or ii) as appropriate.

It is interesting to note that if M

= M

, then the critical d isk

D(M

, M

) collapses to the critical point −1/M

+ 0, and hence, the circle

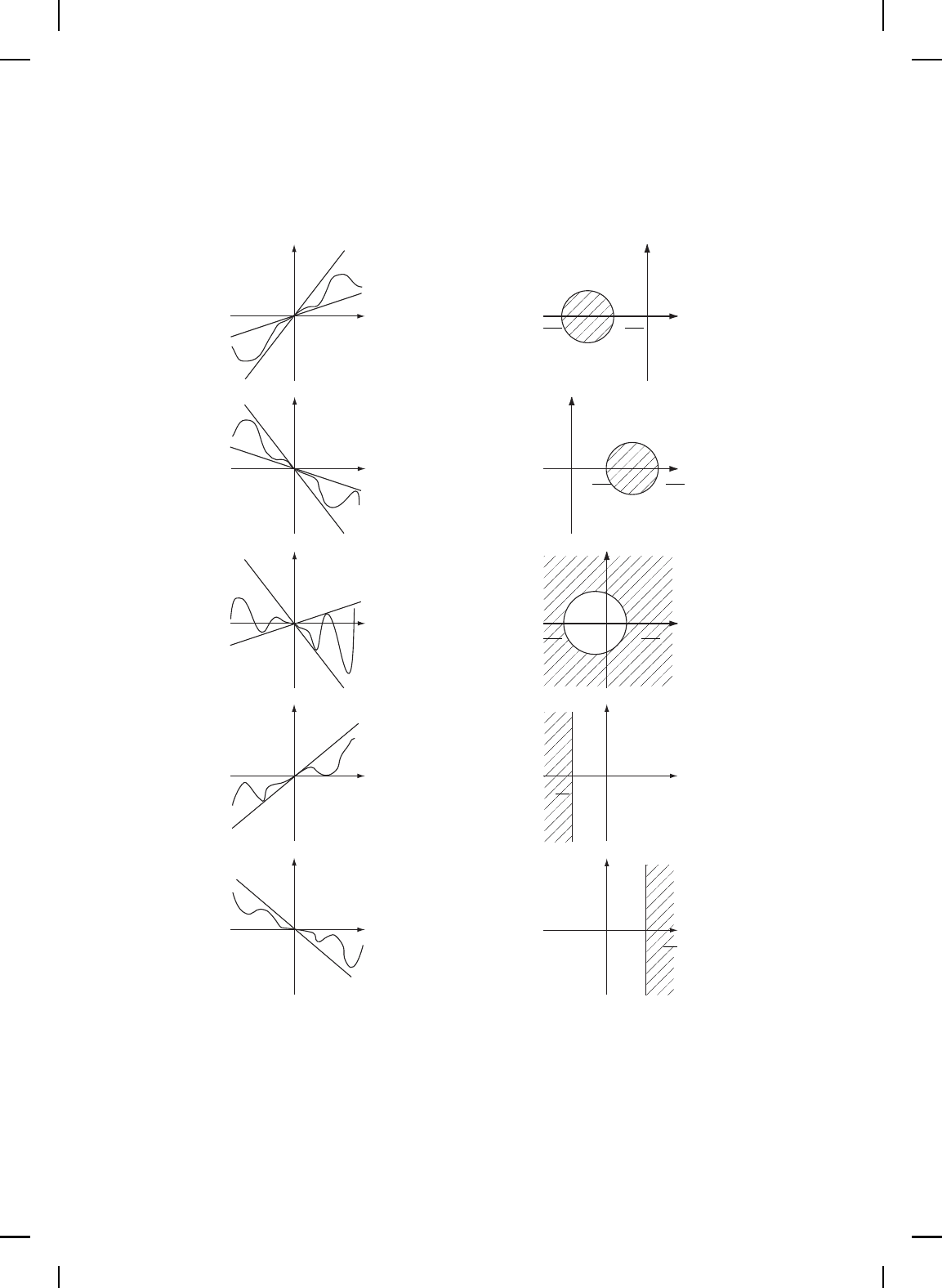
criterion redu ces to the suﬃciency portion of the Nyquist criterion. Figure

5.6 shows the ﬁve diﬀerent cases addressed in Theorem 5.19 along with the

associated f orbidden regions in the Nyquist plane.

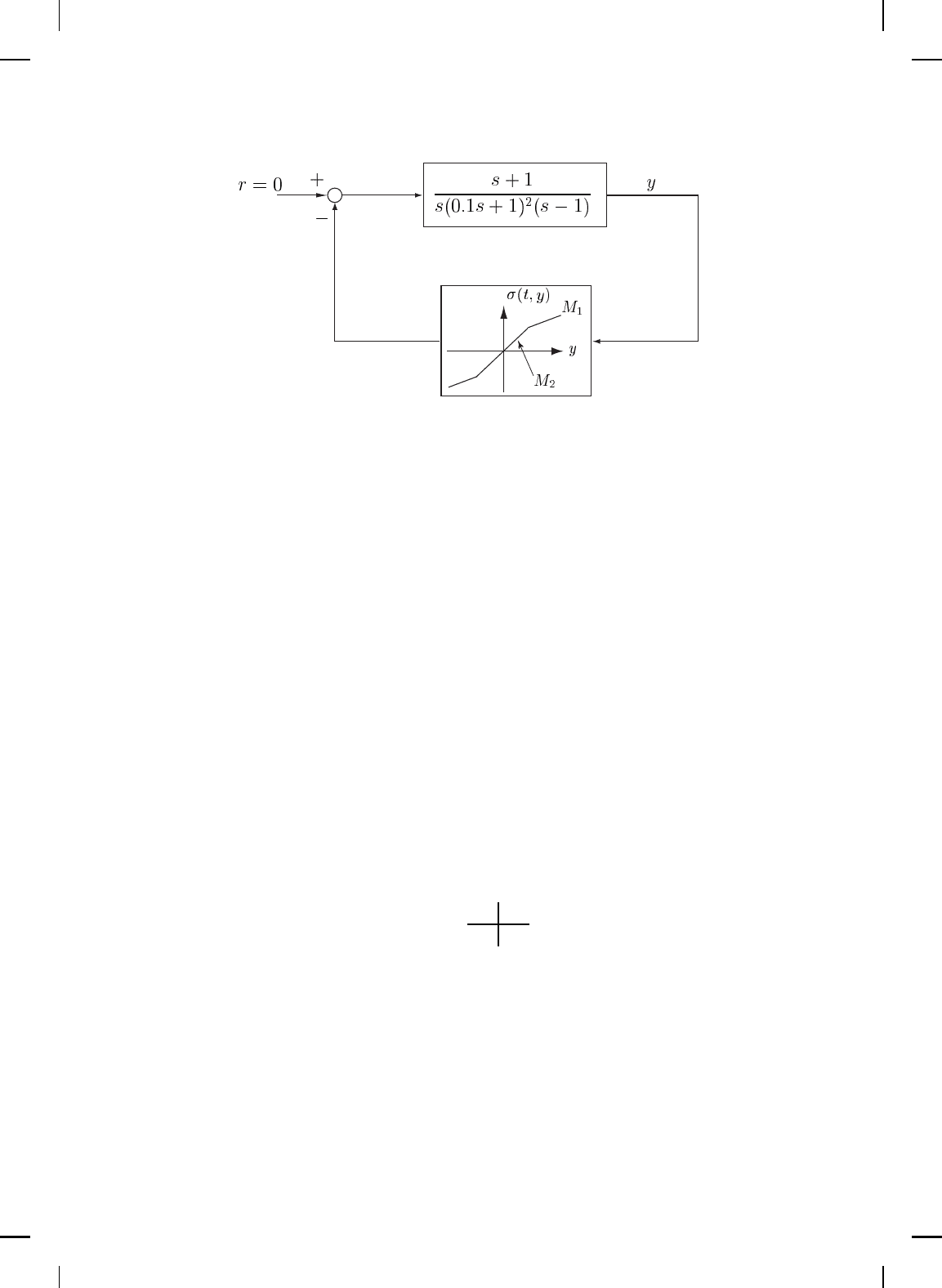
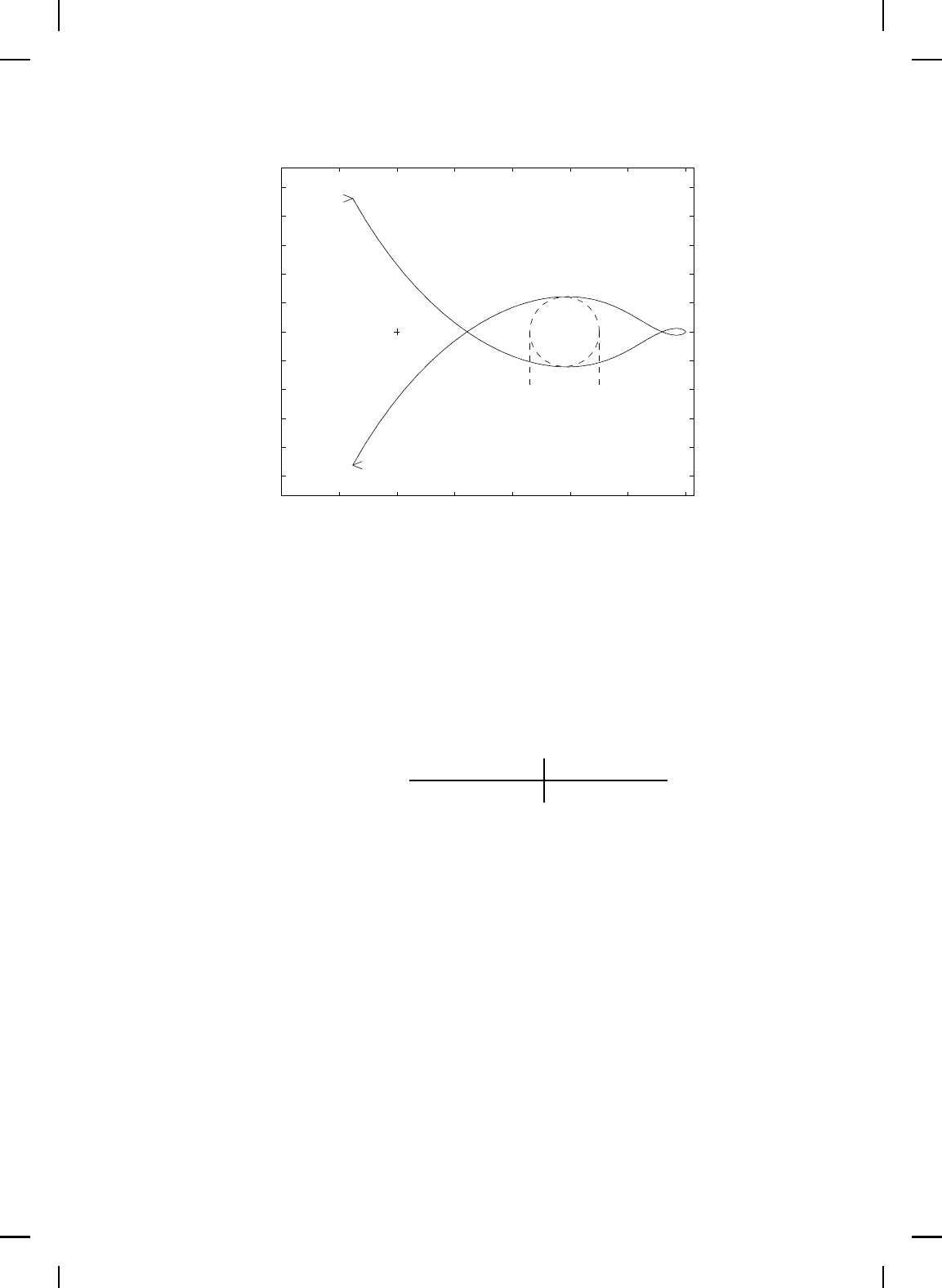
Example 5.8. Consider the linear dyn amical system

G(s) =

s + 1

s(0.1s + 1)

(s −1)

with feedback nonlinearity shown in Figure 5.7. The Nyquist plot of G(ω)

is shown in Figure 5.8. Since G(s) has one pole in the open right half

plane we use i) of the circle criterion. Speciﬁcally, we need to construct a

disk D(M

, M

) such that the Nyquist plot does not enter D(M

, M

) and

encircles it once counterclockwise. Inspecting the Nyquist plot of G(ω)

shows that the disk D(1.85, 3.34) is encircled once in the counterclockwise

direction by the left lobe of the Nyquist plot. Hence, we conclude that the

system is exponentially stable f or the nonlinearity shown in Figure 5.7 with

slopes M

= 1.85 and M

= 3.34. △

5.9 The Popov Criterion

In this section, we present another absolute stability criterion known as

the Pop ov criterion. Although often discussed in juxtaposition with the

circle criterion, the Popov criterion is fundamentally distinct from the circle

criterion in regard to its Lyapunov function foundation. Whereas the sm all

gain, positivity, and circle results are based upon ﬁxed quadratic Lyapunov

functions, the Popov result is based upon a Lyapunov function that is a

function of the sector-bounded nonlinearity. In particular, in the sin gle-input

single-output case, the Popov criterion is based upon the Lur´e-Postnikov

Lyapunov function having the form

V (x) = x

P x + N

σ(s)ds, (5.218)

where P > 0, N > 0, y = Cx, and σ(·) is a scalar memoryless time-invariant

nonlinearity belonging to the sector [0, M]. T hus, in eﬀect, the Popov result

guarantees stability by m eans of a family of Lyapunov functions and, hence,

does not in general apply to time-varying n on linearities.

To present the multivariable Popov criterion, consider the dynamical

NonlinearBook10pt November 20, 2007

382 CHAPTER 5

σ(y, t)

Im G

Re G

−

Figure 5.6 Sector nonlinearities and forbidden Nyquist regions.

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 383

Figure 5.7 Feedback connection with multislope nonlinearity.

system

˙x(t) = Ax(t) + Bu(t), x(0) = x

, t ≥ 0, (5.219)

y(t) = Cx(t), (5.220)

where x(t) ∈ R

, u(t) ∈ R

, and y(t) ∈ R

, with feedback nonlinearity

u(t) = −σ(y(t)), (5.221)

where

σ(·) ∈ Φ

△

= {σ : R

→ R

: σ(0) = 0, σ

(y)[σ(y) − My] ≤ 0, y ∈ R

and σ(y) = [σ

), σ

), . . . , σ

)]

}, (5.222)

where M ∈ R

m×m

and M > 0. Note that the components of σ are assumed

to be decoupled. If M = diag[M

, . . . , M

], M

> 0, i = 1, . . . , m, then the

sector condition characterizing Φ

is implied by the scalar sector conditions

0 ≤ σ

≤ M

, y

∈ R, i = 1, . . . , m, (5.223)

where y

∈ R denotes the ith component of y ∈ R

Theorem 5.20 (Popov Crit erion). Consider the nonlinear dynamical

system (5.219)–(5.221). Suppose

G(s) ∼



A B

C 0



is minimal, and assume there exists N = diag[N

, N

, . . . , N

], N

≥ 0,

i = 1, . . . , m, such th at I

+ M(I

+ Ns)G(s) is strictly positive real and

det(I

+ λN) 6= 0, where M = diag[M

, M

, . . . , M

] > 0 and λ ∈ spec(A).

Then, the zero solution x(t) ≡ 0 of the negative feedback interconnection of

(5.219)–(5.221) is globally asymp totically stable for all σ(·) ∈ Φ

Proof. First note that the negative feedback interconnection of

NonlinearBook10pt November 20, 2007

384 CHAPTER 5

−1.2 −1 −0.8 −0.6 −0.4 −0.2 0

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

−0.5394 −0.2994

Re G(jω)

Im G(jω)

Figure 5.8 Nyquist plot for Example 5.8.

(5.219)–(5.221) has the state space representation

˙x(t) = Ax(t) −Bσ(y(t)), x(0) = x

, t ≥ 0, (5.224)

y(t) = Cx(t). (5.225)

Next, noting that (I + N s)G(s) has a diﬀerentiation eﬀect on the plant

transfer function G(s) it follows that the realization of I

+ M (I + Ns)G(s)

is given by

+ M (I + Ns)G(s) ∼



A B

MC + MNCA I

+ M NCB



. (5.226)

Since det(I

+ λN) 6= 0, λ ∈ spec(A), it follows th at the realization given

in (5.226) is minimal. To see this, note that (A, B) is controllable by

assumption. To show that (A, MC +M NCA) is observable or, equivalently,

(A, C + NCA) is observable since M > 0, assume, ad absurdum, that

(A, C + NCA) is not observable. In this case, since det(I

+ λN) 6= 0,

λ ∈ spec(A), it follows that there exists η ∈ C

, η 6= 0, such that

Aη = λη and Cη = 0, which implies that (A, C) is not observable, and

hence, contradicts the minimality assumption of G(s).

Next, it follows from Theorem 5.14 that if I

+ M(I

+ Ns)G(s) is

strictly positive real, then there exists matrices P ∈ R

n×n

, L ∈ R

p×n

, and

W ∈ R

p×m

, with P positive deﬁnite, and a scalar ε > 0 such that

0 = A

P + P A + εP + L

L, (5.227)