Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 365

Proof. First, we show that i) implies ii). Suppose G(s) is positive real.

Then it follows from Parseval’s theorem that, for all T ≥ 0 and truncated

input function

(t) =



u(t), 0 ≤ t ≤ T,

0, t < 0, t > T,

(5.171)

(t)u(t)dt =

∞

−∞

(t)u

(t)dt

2π

∞

−∞

∗

(ω)u

(ω)dω

4π

∞

−∞

∗

(ω)[G(ω) + G

∗

(ω)]u

(ω)dω

≥ 0,

which implies that G(s) is p assive.

Next, we show that ii) implies iii). If G(s) is passive, then it follows

from Corollary 5.6 with f(x) = Ax, G(x) = B, h(x) = Cx, J(x) = D, that

there exist matrices P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

, with P positive

deﬁnite, such that (5.167)–(5.169) are satisﬁed.

Next, to show that iii) implies i), note that if there exist matrices

P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

, with P positive deﬁnite, such that

(5.167)–(5.169) are satisﬁed, then, for all Re[s] > 0,

G(s) + G

∗

(s)

= C(sI

− A)

−1

B + D + B

∗

− A)

−T

+ D

= W

W + (B

P + W

L)(sI

− A)

−1

∗

− A)

−T

(P B + L

W )

= W

W + W

L(sI

−A)

−1

B + B

∗

− A)

−T

∗

− A)

−T

[(s

∗

− A)

P + P (sI

− A)](sI

− A)

−1

= W

W + W

L(sI

−A)

−1

B + B

∗

− A)

−T

∗

− A)

−T

L + 2Re[s]P ](sI

−A)

−1

≥ [W + L(sI

− A)

−1

∗

[W + L(sI

− A)

−1

≥ 0.

To show analyticity of the entries of G(s) in Re[s] > 0 note that an entry

of G(s) will have a pole at s = λ only if λ ∈ spec(A). Now, it follows from

(5.167) and the fact that P > 0 that all eigenvalues of A have nonpositive

real parts. Hence, G(s) is analytic in Re[s] > 0, which implies that G(s)

is positive real. Finally, (5.170) follows from (5.119) with the linearization

given above.

NonlinearBook10pt November 20, 2007

366 CHAPTER 5

Theorem 5.14 (S trict Positive Real Lemma). Consider th e linear

dynamical system

G(s)

min

∼



A B

C D



with input u(·) ∈ U and output y(·) ∈ Y. Then the following statements are

equivalent:

i) G(s) is strictly positive real.

ii)

εt

(t)y(t)dt ≥ 0, T ≥ 0 ε > 0.

iii) There exist matrices P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

, with P

positive deﬁnite, and a scalar ε > 0 su ch that

0 = A

P + P A + εP + L

L, (5.172)

0 = P B − C

+ L

W, (5.173)

0 = D + D

− W

W. (5.174)

Furth ermore, G(s) is strongly positive real if and only if there exist n × n

positive-deﬁnite matrices P and R such that

0 = A

P + P A + (B

P − C)

(D + D

)

−1

P −C) + R. (5.175)

Proof. The equivalence of i) and iii) is a direct consequence of

Theorem 5.13 by n oting that G(s) is strictly positive real if and only if

there exists ε > 0 such that

G(s − ε/2)

min

∼



A +

εI

C D



is positive real. The fact that iii) implies ii) follows f rom Corollary 5.4 with

f(x) = Ax, G(x) = B, h(x) = Cx, J(x) = D, V

(x) = x

P x, ℓ(x) =

Lx, an d W(x) = W . To show that ii) implies iii), note that if G(s) is

exponentially passive, then it follows from Theorem 5.10 with f(x) = Ax,

G(x) = B, h(x) = Cx, J(x) = D, Q = 0, S = I

, and R = 0, that

there exist matrices P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

, with P positive

deﬁnite, such that (5.172)–(5.174) are satisﬁed.

Finally, with the linearization given above, it follows from (5.140) that

G(s) is strongly positive real if and only if there exist a scalar ε > 0 and a

positive-deﬁnite matrix P ∈ R

n×n

such that

0 ≥ A

P + P A + εP + (B

P − C)

(D + D

)

−1

P − C). (5.176)

Now, if there exist a scalar ε > 0 and a positive-deﬁnite matrix P ∈ R

n×n

such that (5.176) is satisﬁed, then there exists an n × n positive-deﬁnite

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 367

matrix R such that (5.175) is satisﬁed. Conversely, if there exists an n ×

n positive-deﬁnite matrix R such that (5.175) is satisﬁed then, with ε =

min

(R)/σ

max

(P ), (5.175) implies (5.176). Hence, G(s) is strongly positive

real if and only if there exist n × n positive-deﬁnite matrices P and R such

that (5.175) is satisﬁed.

Next, we present analogous results for bounded real systems.

Theorem 5.15 (Bounded Real Lemma). C on s ider the linear dynam-

ical system

G(s)

min

∼



A B

C D



with input u(·) ∈ U and output y(·) ∈ Y. Then the following s tatements are

equivalent:

i) G(s) is bounded real.

ii)

(t)y(t)dt ≤ γ

(t)u(t)dt, T ≥ 0, γ > 0.

iii) There exist matrices P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

, with P

positive deﬁnite, such that

0 = A

P + P A + C

C + L

L, (5.177)

0 = P B + C

D + L

W, (5.178)

0 = γ

− D

D − W

W. (5.179)

If, alternatively, γ

− D

D > 0, then G(s) is bounded real if and only if

there exists an n ×n positive-deﬁnite matrix P such that

0 ≥ A

P + P A + C

C + (B

P + D

(γ

− D

−1

P + D

C).

(5.180)

Proof. First, we show that i) implies ii). Suppose G(s) is bounded

real. Then it follows from Parseval’s theorem that, for all T ≥ 0 and

truncated input function u

(·) given by (5.171),

(t)y(t)dt =

∞

−∞

(t)y(t)dt

2π

∞

−∞

∗

(ω)y(ω)dω

2π

∞

−∞

∗

(ω)G

∗

(ω)G(ω)u

(ω)dω

≤

2π

∞

−∞

∗

(ω)u

(ω)dω

NonlinearBook10pt November 20, 2007

368 CHAPTER 5

= γ

(t)u(t)dt,

which implies that G(s) is n on exp ansive.

Next, we show that ii) implies iii). If G(s) is nonexpansive, then

it follows from Corollary 5.7 with f (x) = Ax, G(x) = B, h(x) = Cx,

J(x) = D, that there exist matrices P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

with P positive deﬁnite, such that (5.177)–(5.179) are satisﬁed.

Now, to show that iii) implies i), note that if there exist matrices

P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

, with P positive deﬁnite, such that

(5.177)–(5.179) are satisﬁed, then, for all Re[s] ≥ 0,

− G

∗

(s)G(s)

= γ

− [C(sI

− A)

−1

B + D]

∗

[C(sI

− A)

−1

B + D]

= [γ

− D

D] − [C(sI

− A)

−1

∗

[C(sI

− A)

−1

−[C(sI

− A)

−1

∗

D − D

[C(sI

− A)

−1

= W

W + [B

P + W

L](sI

− A)

−1

B + B

(sI

− A)

−∗

·[P B + L

W ] − B

(sI

− A)

−∗

C(sI

− A)

−1

= W

W + W

L(sI

−A)

−1

B + B

(sI

− A)

−∗

−B

(sI

− A)

−∗

C(sI

− A)

−1

(sI

− A)

−∗

[(sI

− A)

∗

P + P (sI

− A)](sI

− A)

−1

= W

W + W

L(sI

−A)

−1

B + B

(sI

− A)

−∗

(sI

− A)

−∗

L(sI

− A)

−1

+2Re[s]B

(sI

− A)

−∗

P (sI

− A)

−1

≥ [W + L(sI

−A)

−1

∗

[W + L(sI

− A)

−1

≥ 0.

To show analyticity of the entries of G(s) in Re[s] ≥ 0 note that it f ollows

from (5.177) and the fact that P > 0 and (A, C) is ob s ervable that all

the eigenvalues of A have negative real parts. Hence, G(s) is analytic in

Re[s] ≥ 0, which implies that G(s) is bounded real. Finally, (5.180) follows

from (5.131) with the linearization given above.

Theorem 5.16 (Strict Bounded Real Lemma). Consider the linear

dynamical system

G(s)

min

∼



A B

C D



with input u(·) ∈ U and output y(·) ∈ Y. Then the following statements are

equivalent:

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 369

i) G(s) is strictly bounded r eal.

ii)

εt

(t)y(t)dt ≤ γ

εt

(t)u(t)dt, T ≥ 0, γ > 0, ε > 0.

iii) There exist matrices P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

, with P

positive deﬁnite, such that

0 = A

P + P A + εP + C

C + L

L, (5.181)

0 = P B + C

D + L

W, (5.182)

0 = γ

−D

D − W

W. (5.183)

Furth ermore, G(s) is strongly bounded real if an d only if there exist n × n

positive-deﬁnite matrices P and R such that

0 = A

P +P A+C

C +(B

P +D

(γ

−D

−1

P +D

C)+R.

(5.184)

Proof. The equivalence of i) and iii) is a direct consequence of

Theorem 5.15 by noting that G(s) is strictly bounded real if and only if

there exists ε > 0 such that

G(s −ε/2)

min

∼



A +

εI

C D



is bounded real. The fact that iii) implies ii) follows from Corollary 5.5

with f(x) = Ax, G(x) = B, h(x) = Cx, J(x) = D, V

(x) = x

P x, ℓ(x) =

Lx, and W(x) = W . To show that ii) implies iii), note that if G(s) is

exponentially nonexpansive, then it follows from Theorem 5.10 with f(x) =

Ax, G(x) = B, h(x) = Cx, J(x) = D, Q = −I

, S = 0, and R = γ

, that

there exist matrices P ∈ R

n×n

, L ∈ R

p×n

, and W ∈ R

p×m

, with P positive

deﬁnite, such that (5.181)–(5.183) are satisﬁed.

Finally, with the linearization given above, it follows from (5.144) that

G(s) is strongly bounded real if and only if there exist a scalar ε > 0 and a

positive-deﬁnite matrix P ∈ R

n×n

such that

0 ≥ A

P + P A + εP + (B

P −C)

(D + D

)

−1

P − C). (5.185)

Now, if there exist a scalar ε > 0 and a positive-deﬁnite matrix P ∈ R

n×n

such that (5.185) is satisﬁed, then there exists an n × n positive-deﬁnite

matrix R such that (5.184) is satisﬁed. Conversely, if there exists an n ×

n positive-deﬁnite matrix R such that (5.184) is satisﬁed then, with ε =

min

(R)/σ

max

(P ), (5.184) implies (5.185). Hence, G(s) is strongly bounded

real if and only if there exist n × n positive-deﬁnite matrices P and R such

that (5.184) is satisﬁed.

As noted earlier, strict bounded realness is equivalent to G(s) asymp-

totically stable and G

∗

(ω)G(ω) < γ

, ω ∈ R. However, as in the positive

NonlinearBook10pt November 20, 2007

370 CHAPTER 5

real case, th e frequency domain test for strict positive realness is subtle and

does n ot simply involve checking He G(ω) > 0, ω ∈ R. To see this, consider

the transfer function

G(s) =

s + (α + β)

(s + α)(s + β)

, (5.186)

where α, β > 0. Noting that

He G(ω) =

αβ(α + β)

(ω

+ α

)(ω

+ β

)

, (5.187)

it follows that He G(ω) > 0, ω ∈ R. Now, it can be easily shown, using the

deﬁnition of positive realness, that G(s) is positive real. However, for ε > 0

it follows that

He G(ω − ε) =

−εω

+ (α − ε)(β − ε)(α + β − ε)

(ω

+ (α − ε)

)(ω

− (β − ε)

)

, (5.188)

which, for suﬃciently large ω, is negative, and hence, G(s−ε) is not positive

real. Hence, even though He G(ω) > 0, ω ∈ R, G(s) is not strictly positive

real. In light of the above, we characterize necessary and suﬃcient conditions

for a transfer function to be strictly positive r eal in terms of a frequency

domain test. For the statement of the next result recall that a rational

transfer function G(s) is nonsingular if and only if det G(s) is not the zero

polynomial. Equivalently, det G(s) is not zero if and only if the normal

rank of G(s) ∈ C

m×m

over the ﬁeld of rational functions of s is m, th at is,

nrank G(s)

△

= max

s∈C

rank

G(s) = m.

Theorem 5.17. Let

G(s) ∼



A B

C D



be an m×m rational transfer function and suppose that G(s) is not singular.

Then, G(s) is strictly p ositive real if and only if the following conditions hold:

i) No entry of G(s) has a pole in Re[s] ≥ 0.

ii) He G(ω) > 0 for all ω ∈ R.

iii) Either D+D

> 0 or both D+D

≥ 0 and lim

ω →∞

[He G(ω)]Q

> 0 for every Q ∈ R

m×(m−q)

, where q = rank(D + D

), such that

(D + D

)Q = 0.

Proof. Suppose i)–iii) hold. Let ε > 0 and note that

G(s − ε) = C((s − ε)I − A)

−1

B + D

= C(sI − A)(sI − A)

−1

(sI − (A + εI))

−1

B + D

= C(sI − A)

−1

(sI − (A + εI) + εI)(sI − (A + εI))

−1

B + D

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 371

= G(s) + εG

(s), (5.189)

where G

(s)

△

= C(sI − A)

−1

(sI − (A + εI))

−1

B. S ince A is Hurwitz, sI −

A is nonsingular for all s = ω and there exists ˆε such th at sI − (A +

εI) is nonsingular for all ε ∈ [0, ˆε] and for all s = ω. Hence, f (ω, ε)

△

max

|λ

[He G

(ω)]| is ﬁnite for all ε ∈ [0, ˆε] and for all ω ∈ R. Since

lim

ω →∞

f(ω, ε) = 0 for all ε ∈ [0, ˆε], it follows that there exists k

> 0 su ch

that f (ω, ε) < k

for all ε ∈ [0, ˆε] and for all ω ∈ R, and hence, −k

≤

He G

(σ) ≤ k

for all ε ∈ [0, ˆε] and for all s = ω. Now, if D + D

> 0,

and since He G(ω) > 0 f or all ω ∈ R and lim

ω →∞

He G(ω) = D + D

> 0,

it follows th at there exists k

> 0 such that He G(ω) ≥ k

> 0, ω ∈ R.

Choosing 0 < ε < min{ˆε,

}, it follows that

He G(s −ε) = He G(s) + εHe G

(s) ≥ k

−εk

> 0, (5.190)

for all s = ω. Hence, G(s −ε) is positive real, and thus, by deﬁnition, G(s)

is strictly positive real.

Alternatively, if det(D + D

) = 0, it follows from iii) that He G(ω)

has q eigenvalues λ(ω) satisfying lim

ω →∞

λ(ω) > 0 and m − q eigenvalues

satisfying lim

ω →∞

λ(ω) = 0 and lim

ω →∞

λ(ω) > 0. Hence, there exists

> 0 for some ˆω > 0 such that ω

min

[He G(ω)] ≥ k

for all |ω| ≥ ˆω.

Furth ermore, since lim

ω →∞

(ω) exists and −k

≤ He G

(ω) ≤

for all ω ∈ R and ε ∈ [0, ˆε], it follows that there exist k

> 0 and

∗

> 0 such that −k

≤ He G

(ω) ≤ k

for all |ω| ≥ ω

∗

and ε ∈ [0, ˆε].

Hence,

He(ω − ε) = ω

He G(ω) + ω

εHe G

(ω) ≥ k

− εk

|ω| ≥ ω

, (5.191)

where ω

= max{ˆω, ω

∗

}. S ince He G(ω) > 0, ω ∈ R, it follows that

min

[He G(ω)] ≥ k

> 0 for all ω ∈ [−ω

, ω

]. Hence, usin g the fact th at

−k

≤ He G

(ω) ≤ k

for all ω ∈ R it follows that He G(ω − ε) ≥

− εk

for all |ω| ≤ ω

. Now, taking 0 < ε < min{

}, it follows that

He G(ω − ε) > 0, ω ∈ R. Hence, G(s − ε) is positive real, and hence, G(s)

is strictly positive real.

Conversely, suppose G(s) is strictly positive real and let ε > 0 be such

that G(s − ε) is positive real. Note that G(s) is asymptotically stable and

positive real. Hence, He G(ω) ≥ 0, ω ∈ R, and He G(∞) = D + D

≥ 0.

Now, let (A, B, C, D) be a minimal realization of G(s). Using Theorem 5.14,

it follows fr om (5.172)–(5.173) that

G(s) + G

∗

(s) = D + D

+ C(sI − A)

−1

B + B

∗

I − A)

−T

= W

W + (W

L + B

P )(sI − A)

−1

∗

I − A)

−T

(P B + L

W )

NonlinearBook10pt November 20, 2007

372 CHAPTER 5

= W

W + W

L(sI − A)

−1

B + B

∗

I − A)

−T

∗

I − A)

−T

[(s

∗

+ s)P − A

P − P A](sI − A)

−1

= W

W + +W

L(sI − A)

−1

B + B

∗

I − A)

−T

∗

I − A)

−T

L + εP )(sI − A)

−1

+(s

∗

+ s)B

∗

I − A)

−T

P (sI − A)

−1

= [W + L(sI − A)

−1

∗

[W + L(sI − A)

−1

+(2Re[s] + ε)B

∗

I − A)

−T

P (sI − A)

−1

B. (5.192)

Now, suppose, ad absurdum, that He G(ω) is not positive deﬁnite

for all ω ∈ R. Then , for some ω = ˆω there exists x ∈ C

, x 6= 0,

such that x

∗

[He G(ω)]x = 0. In this case, it follows from (5.192) that

Bx = 0 and W x = 0. Hence, x

∗

[He G(s)]x = 0 for all s ∈ C, and hence,

det[He G(s)] ≡ 0, which leads to a contradiction. Thus, He G(ω) > 0,

ω ∈ R. Now, if He G(∞) = D + D

> 0 the resu lt is immediate.

Alternatively, let Q ∈ R

m×(m−q)

be a full row rank matrix su ch that

(D + D

)Q = Q

W Q = 0. Hence, W Q = 0 and by (5.192),

[He G(ω)]Q = Q

(ωI − A)

−∗

L + εP ](ωI − A)

−1

BQ. (5.193)

Now, since He G(ω) > 0, ω ∈ R, and Q is full r ow rank it follows that BQ

is full column rank. Usin g (5.193) it follows that

lim

ω →∞

[He G(ω)]Q = Q

L + εP )BQ > 0, (5.194)

which proves the result.

Note that if D +D

= 0 then we can take Q = I

in Theorem 5.17. It

follows from Theorem 5.17 that a necessary and suﬃcient frequen cy domain

test for a scalar strictly positive real sys tem is Re G(ω) > 0, ω ∈ R, if

D > 0, and Re G(ω) > 0, ω ∈ R, and lim

ω →∞

Re G(ω) > 0 if D = 0.

5.7 Absolute Stability Theory

Absolute stability theory guarantees stability of feedback systems whose

forward path contains a dynamic linear time-invariant system and whose

feedback path contains a memoryless (possibly time-varying) nonlinearity

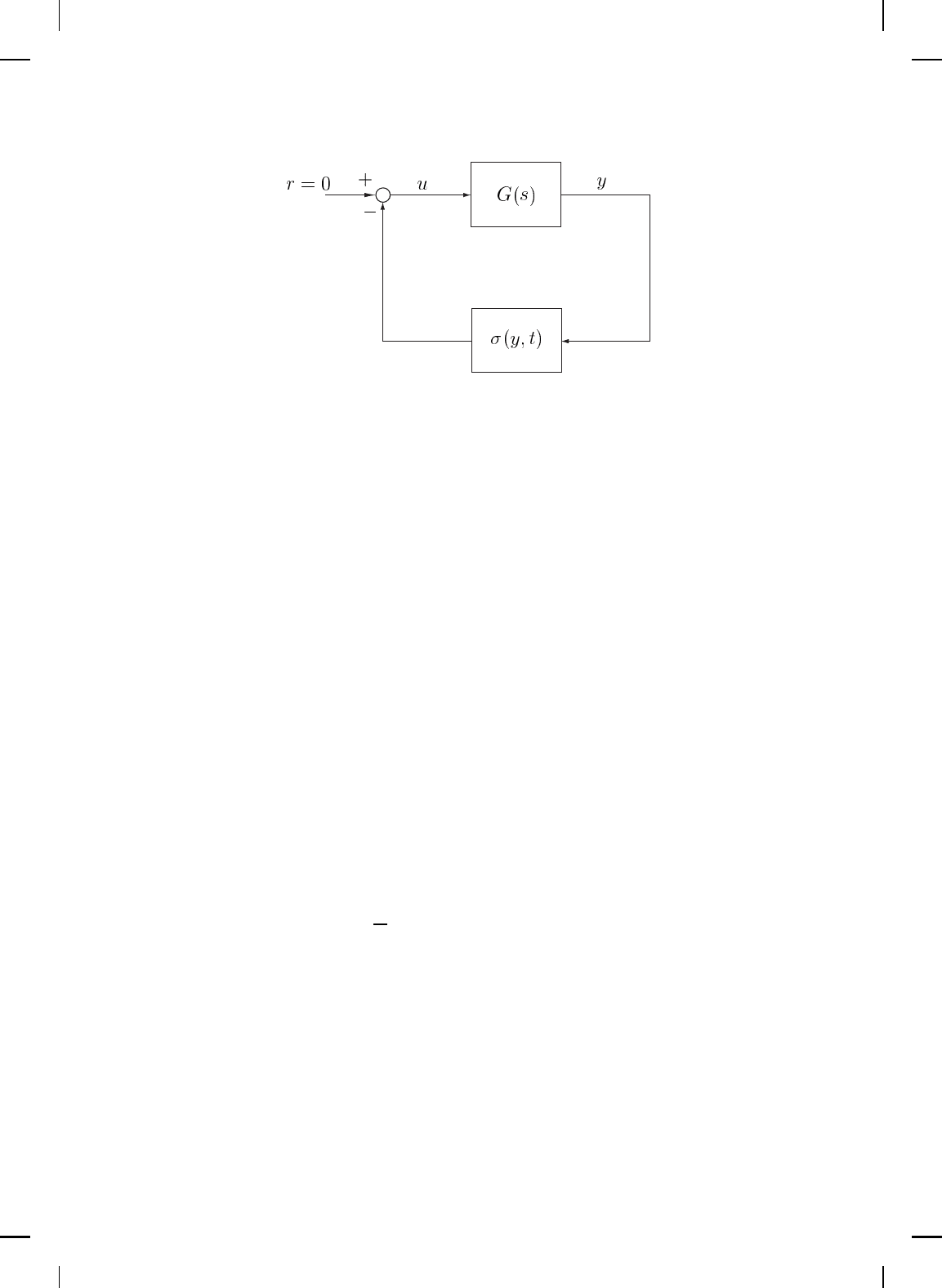
(see Figure 5.1). These stability criteria are generally stated in terms of the

linear system and apply to every element of speciﬁed class of nonlinearities.

Hence, absolute stability theory provides suﬃcient conditions for robust

stability with a given class of uncertain elements.

The literature on absolute stability is extensive. Two of the most

fundamental results concerning the stability of feedback systems with memo-

ryless nonlinearities are the circle criterion, which includes the positivity and

NonlinearBook10pt November 20, 2007

DISSIPATIVITY THEORY FOR NONLINEAR SYSTEMS 373

Figure 5.1 Feedback system with a static nonlinearity.

small gain theorems as special cases, and the Popov criterion. A convenient

way of distinguishing these results is to focus on the allowable class of

feedback nonlinearities. Speciﬁcally, the small gain, positivity, and circle

theorems guarantee stability for arbitrarily time-varying nonlinearities,

whereas the Popov criterion does not. This is n ot surprising since as will

be shown the Lyapunov function upon which the small gain, positivity, and

circle theorems are based is a ﬁxed quadratic Lyapunov function, which

permits arbitrary time variation of the nonlinearity. Alternatively, the

Popov criterion is based on a Lur´e-P ostnikov Lyapunov function which

explicitly depends on th e feedback nonlinearity thereby restricting its

allowable time variation.

In this section, we present the abs olute stability problem for feedback

systems with time-varying memoryless input nonlinearities. Speciﬁcally, the

forward path of the dynamical s ystem is described by

˙x(t) = Ax(t) + Bu(t), x(0) = x

, t ≥ 0, (5.195)

y(t) = Cx(t) + Du(t), (5.196)

where x(t) ∈ R

, u(t) ∈ R

, y(t) ∈ R

, and the feedback interconnection is

given by

u(t) = −σ(y(t), t), (5.197)

where

σ(·, ·) ∈ Φ

△

= {σ : R

×R

→ R

: σ(0, ·) = 0, [σ(y, t) − M

[σ(y, t)

−M

y] ≤ 0, y ∈ R

, a.e. t ≥ 0, and σ(y, ·) is Lebesgue

measurable f or all y ∈ R

}, (5.198)

where M

, M

∈ R

m×l

. We say that σ(·, ·) belongs to the sector [M

, M

]

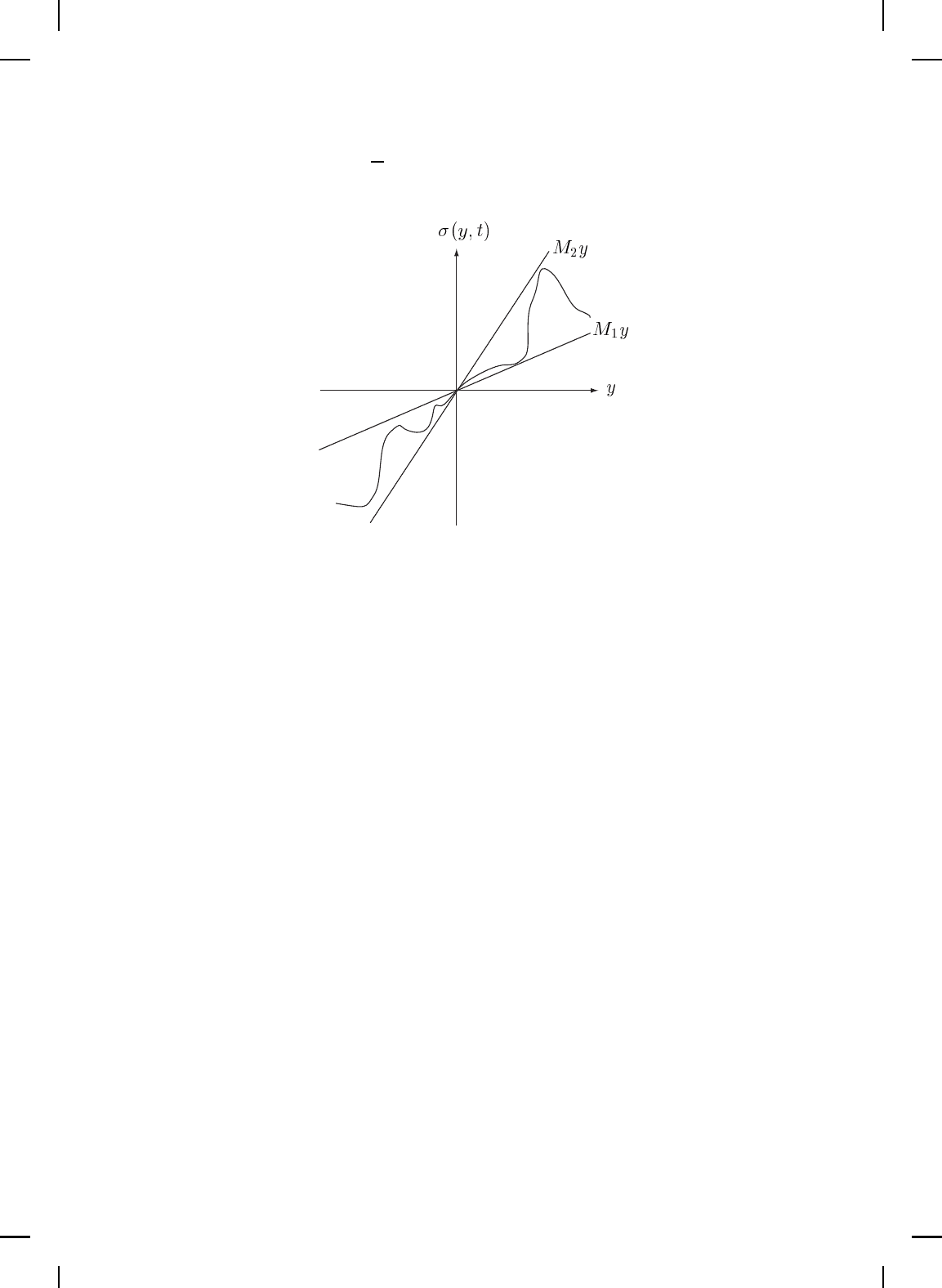
if and only if σ(·, ·) ∈ Φ. Note that in the single-input, single-output case

m = l = 1, the sector condition characterizing Φ is equivalent to

≤ σ(y, t)y ≤ M

, y ∈ R, a.e. t ≥ 0. (5.199)

NonlinearBook10pt November 20, 2007

374 CHAPTER 5

In this case, for each t ∈ R

, the graph of σ(y, t) lies in between two s traight

lines of slopes M

and M

, respectively (see Figure 5.2).

Figure 5.2 Sector-bounded nonlinearity σ(y, t).

Now, the absolute stability problem, also known as the Lur´e problem,

can be stated as follows. Given the dynamical system (5.195) and (5.196)

where (A, B, C) is minimal and given M

, M

∈ R

m×l

, derive conditions

involving only the forward path (5.195) and (5.196) and the sector bounds

, M

, such that the zero s olution x(t) ≡ 0 of the feedback interconnection

(5.195)–(5.197) is globally uniformly asymptotically stable for all σ(·, ·) ∈ Φ.

In an attempt to solve the absolute stability problem by examining the

stability of all linear time-invariant systems within the family of nonlinear

time-varying systems, in 1949 the Russian mathematician M. A. Aizerman

made the following conjecture.

Conjecture 5.1 (Aizerman’s Conjecture). Consider the nonlinear

dynamical system (5.195)–(5.197) with σ(y, t) = σ(y) ∈ Φ, D = 0, and

m = l = 1. If the zero solution x(t) ≡ 0 to (5.195)–(5.197) with σ(y) = F y,

where F ∈ [M

, M

], is asymptotically stable, then the zero solution x(t) ≡ 0

to (5.195)–(5.197) is globally asymptotically stable for all σ(·) ∈ Φ.

This conjecture is false. Motivated by Aizerman’s conjecture, in 1957

R. E. Kalman m ade a reﬁnement to this conjecture.

Conjecture 5.2 (Kalman’s Conjecture). Consider the nonlinear dy-

namical system (5.195)–(5.197) with σ(y, t) = σ(y), D = 0, and m = l = 1.

Furth ermore, assume σ : R → R is such that M

≤ σ

′

(y) ≤ M

for all y ∈ R.

If the zero solution x(t) ≡ 0 to (5.195)–(5.197) with σ(y) = F y, where