Гюннер Э.А., Шульгин В.Ф. Общая химия
Подождите немного. Документ загружается.

Следующей предпосылкой рассматриваемой теории явилось объяснение закономерностей фотоэффекта -
испускания электронов при облучении поверхности металла светом. Экспериментально было установлено, что
кинетическая энергия фотоэлектронов зависит от частоты излучения, но не зависит от его интенсивности (от
интенсивности излучения зависит только число электронов, т.е. сила фототока), хотя в рамках классической
электромагнитной теории света энергия фотоэлектронов должна меняться с изменением интенсивности
падающего света и не должна зависеть от частоты излучения. А. Эйнштейн (1905) показал, что это противоречие
можно устранить, если принять, что свет имеет двойственную природу, являясь одновременно пакетом
электромагнитных волн, энергия которых описывается уравнением Планка (2-1), и потоком фотонов - частиц с
нулевой массой покоя. В этом случае кинетическая энергия фотоэлектрона будет определяться следующим
соотношением:
Е
к
= Е
ф
– А
где Е
ф
- энергия фотона, А - работа, которую необходимо затратить на удаление электрона из металла (работа
выхода).
С учетом уравнения (2-1)
Е
к
= h - А
то есть энергия фотоэлектронов зависит от частоты излучения и не зависит от его интенсивности.
Третьей предпосылкой квантовой механики является ядерная (планетарная) модель атома, предложенная Э.
Резерфордом (1911), в соответствии с которой атом представляет систему из положительно заряженного ядра и
связанных с ним электронов. Хотя от "планетарного" характера движения электронов вокруг ядра позже
пришлось отказаться (подобное движение электрона должно было сопровождаться непрерывным излучением
энергии, следствием чего было бы непрерывное уменьшение радиуса электронной орбиты и в конечном итоге
падение электрона на ядро), ядерная модель атома остается общепризнанной.
В 1913 г. Н. Бор показал, что устойчивость атома водорода и происхождение линий в его спектре могут быть
объяснены, если допустить, что разрешенные значения энергии электрона меняются дискретно, а
энергетическим уровням отвечают стационарные орбиты определенного радиуса, пребывая на которых электрон
не поглощает и не излучает энергию. Теория Бора позволила с высочайшей степенью точности рассчитать
атомный спектр водорода, однако распространить ее на другие атомы не удалось. Таким образом к началу
двадцатых годов XX века необходимость в новом подходе к описанию объектов микромира стала очевидной.
2.2. Постулаты квантово-механической теории
Квантово-механическая теория является основополагающей концепцией, принципы которой не могут быть
выведены из каких-либо более общих теоретических построений. В соответствии с этим в основе квантовой
механики, как и в основе любой другой фундаментальной теории, лежат постулаты - положения, справедливость
которых гарантируется опытом, хотя они и не могут быть строго доказаны. Такими постулатами квантовой
механики являются принцип корпускулярно-волнового дуализма и принцип неопределенности.
Принцип корпускулярно-волнового дуализма может быть сформулирован следующим образом (Луи де
Бройль, 1924): каждому движущемуся материальному объекту можно поставить в соответствие волновой
процесс. Если это положение справедливо, то должно существовать уравнение, связывающее корпускулярные
свойства объекта (масса, скорость) с волновыми (длина волны или частота). Такое уравнение может быть строго
выведено для фотона, частицы, движению которой соответствует распространение электромагнитной волны.
Поскольку для фотона масса покоя равна нулю, а скорость движения частицы и скорость распространения волны
одинаковы (с = 310
8
м/с), энергия фотона может быть найдена как из уравнения Планка (E = h), описывающего
волновой процесс, так и из уравнения Эйнштейна (E = mc
2
), характеризующего фотон как частицу. Приравнивая
правые части этих уравнений и учитывая, что = с, получим
h
c
= mc = p
где р - импульс фотона, откуда
=
h
mc
=
h
p
(2-2)
Принцип де Бройля распространяет уравнение (2-2) на любые частицы, масса покоя которых отличается от
нуля, а скорость (v) - от скорости света. В этом случае
=
h
mv
=
h
p
(2-3).
Волны, соответствующие движущимся частицам, получили название волн материи или волн де Бройля.
Представить физическую сущность волн де Бройля несколько затруднительно. По концепции М. Борна волны де
Бройля являются волнами вероятности: для пучка электронов вероятность появления частицы в определенном
объеме пространства изменяется по волновому закону.
Волны материи могут быть зарегистрированы экспериментально. Так, Девиссон и Джермер (1927)
обнаружили, что пучок электронов, направленный на грань монокристалла никеля, дает при отражении типичную
интерференционную картину. При этом экспериментально определенные значения длин волн совпали с
рассчитанными по уравнению де Бройля. В настоящее время волновые свойства обнаружены экспериментально
у таких частиц как протоны, нейтроны и даже атомы гелия. Для макробъектов длины волн де Бройля очень малы
(порядка 10
-30
-10
-40
м); зарегистрировать такую волну экспериментально не представляется возможным.
11

Вторым основным постулатом квантовой механики является принцип неопределенности, сформулированный
В. Гейзенбергом (1927). В классической физике точность измерения той или иной характеристики объекта
определяется лишь разрешающей способностью используемого прибора и не зависит от того, насколько точно
определены какие-либо другие характеристики объекта. В микромире картина принципиально меняется; в нем
существуют характеристики, точное определение одной из которых препятствует определению другой. Таким
свойством обладают, например, координаты частицы, определяющие ее положение в пространстве, и ее
скорость или импульс. Соотношение неопределенности можно сформулировать следующим образом:
принципиально невозможно одновременно точно определить положение микрочастицы в пространстве и ее
импульс.
Продемонстрируем справедливость этого принципа с помощью следующего мысленного эксперимента.
Пусть движущийся электрон освещают потоком фотонов, а отраженные фотоны регистрируют с помощью некого
идеального детектора, пытаясь таким образом установить координаты и импульс микрочастицы. Положение
частицы в пространстве задается координатами x, y , z, а ее импульс, являющийся векторной величиной, - его
проекциями на координатные оси (p
x
, p
y
, p
z
). Очевидно, что при этом значение импульса будет характеризоваться
некоторой неопределенностью (погрешностью определения), так как при столкновении фотона, имеющего
собственный импульс, с электроном импульс последнего изменится. Точно также измерение координат будет
проведено с некоторой неопределенностью, связанной с дифракцией фотонов на электроне, вследствие чего
образ электрона будет размытым. При этом дифракция будет увеличиваться с увеличением длины волны
излучения. Предположим, что наблюдатель желает максимально сократить неопределенность положения
электрона, уменьшая для этого длину волны фотона. Однако это влечет за собой увеличение частоты излучения
( = с/), а также энергии и импульса фотона, так как
p =
2mE
к
(2-4)
где Е
к
- кинетическая энергия фотона. В результате в силу закона сохранения импульса столкновение с фотоном
существенно изменит импульс электрона, погрешность его определения возрастет, а наблюдаемая траектория
электрона станет зигзагообразной.
к детектору
наблюдаемая
траектория
электрона
h
0
E
С другой стороны, уменьшение неопределенности импульса требует уменьшения импульса фотона, для чего
необходимо уменьшить его энергию, а, следовательно, увеличить длину волны. Результатом этого будет
усиление дифракции, а соответственно, увеличение неопределенности в значениях координат -
экспериментатор увидит вместо точки размытое пятно, и не сможет установить, где именно в пределах этого
пятна будет находится электрон.
к детектору
наблюдаемая
траектория
электрона
h
0
E
Рассмотренный мысленный эксперимент показывает, что одновременно уменьшить неопределенность
импульса и координат электрона принципиально невозможно.
Математически принцип неопределенности для частицы, движущейся в трехмерном пространстве,
выражается тремя неравенствами:
xp
x
yp
y
zp
z
где а и р
а
неопределенности координат и проекций импульса на координатные оси, =
h
2
= 1,0510
-34
Джс.
Заметим, что координаты и импульс - не единственные физические характеристики, связанные принципом
неопределенности. Так, для нестационарных состояний невозможно одновременно точно определить время
существования состояния и его энергию.
Из принципа неопределенности вытекает несколько важных выводов, необходимых для правильного
понимания особенностей микромира:
12
1. Микрочастица не имеет детерминированной (строго определенной) траектории. Для построения траектории
движущегося тела необходимо знать закон, по которому происходит движение, и начальные условия - значения
координат и импульса в какой-то момент времени. Принцип неопределенности это запрещает.
2. В микромире инструмент наблюдения взаимодействует с объектом наблюдения, изменяя его характеристики.
3. Модель атома должна быть вероятностной. Следует отказаться от попыток определить точные значения
характеристик микрочастицы (координат, импульса, энергии и т.) и попытаться установить их вероятные
значения.
При построении вероятностной модели атома пришлось отказаться от понятия "электронная орбита". В
квантовой механике это понятие заменено понятием "электронная орбиталь". Электронная орбиталь - это
область околоядерного пространства, в которой вероятность нахождения электрон существенно
отличается от нуля. Невозможно установить, где именно в пределах орбитали в данный момент находится
электрон, но можно оценить вероятность его пребывания в той или иной точке пространства. Таким образом,
электрон как бы "размазан" (делокализован) в объеме электронной орбитали, образуя электронное облако.
Важнейшими характеристиками электронной орбитали являются ее граничная поверхность и функция
радиального распределения вероятности нахождения электрона. Граничная поверхность определяет форму
электронной орбитали (сфера, объемная восьмерка и т.д.). Обычно граничную поверхность строят таким
образом, чтобы вероятность нахождения электрона в ограниченном ею пространстве составляла 90 или 95%.
Функция радиального распределения показывает вероятность нахождения электрона на разных расстояниях от
ядра. На рис. 1 и 2 показаны граничные поверхности и кривые радиального распределения для некоторых
состояний электрона атома водорода.
Для основного состояния атома водорода (1s) граничная поверхность имеет форму сферы, а кривая
радиального распределения вероятности проходит через максимум при r = 52,9 пм (1 пм = 10
-12
м). Заметим, что
данная величина совпадает с радиусом первой боровской стационарной орбиты. На этом примере
прослеживаются отличия модели атома водорода по Н. Бору от квантово-механической модели - то, что в теории
Бора является радиусом первой стационарной орбиты, в квантовой механике характеризуется как наиболее
вероятное расстояние между электроном и ядром.
13
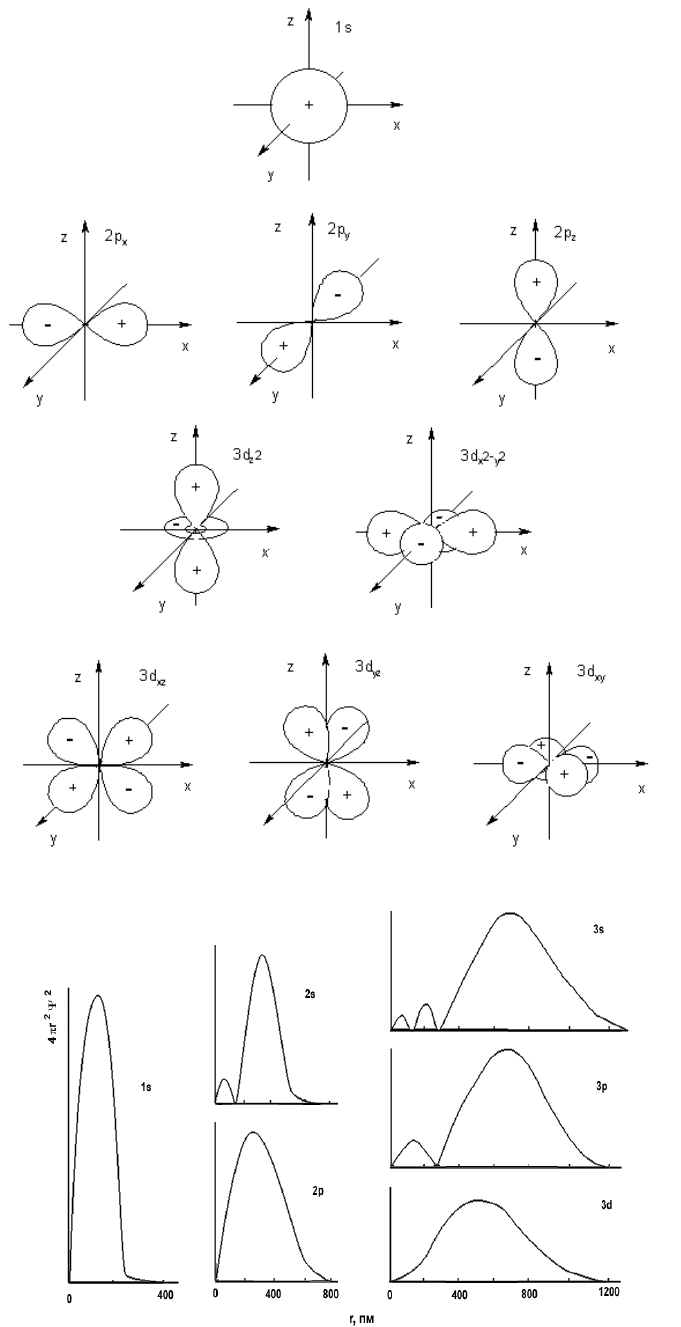
Рис. 1. Форма граничной поверхности s-, p- и d-орбиталей. Указаны также математические знаки
соответствующих волновых функций
Рис. 2. Кривые радиального распределения вероятности нахождения электронов для некоторых орбиталей
атома водорода
14

2.3. Волновая функция. Уравнение Шредингера
Квантовая механика постулирует существование некой специальной функции, с помощью которой могут
быть установлены вероятные значения всех характеристик (координат, импульса, энергии и т.д.) электрона или
иной микрочастицы, определяющих ее состояние. Эта функция обозначается греческой буквой (пси) и
называется волновой функцией или пси-функцией. Волновая функция не имеет простого физического смысла,
однако, как было показано М. Борном, четкий физический смысл имеет ее квадрат. Величина
2
в какой-либо
точке пространства прямо пропорциональна вероятности нахождения (dW) частицы в бесконечно малом
элементе объема (dV), включающем эту точку.
dW
2
dV
Физический смысл квадрата волновой функции налагает определенные ограничения на свойства -функции.
Так, она должна быть конечна, непрерывна и однозначна. Действительно, вероятность нахождения электрона в
той или иной точке всегда конечна и не может принимать несколько значений. Там, где электрон не может
находиться (например, на бесконечно большом расстоянии от ядра), волновая функция должна обращаться в
нуль. Волновая функция, удовлетворяющая условию
1 = dV
2
(2-5)
называется нормированной. Условие (2-4) означает, что вероятность нахождения электрона в бесконечно
большом объеме равна единице, т.е., что этот электрон где-то находится. Если нормированная функция
связана с ненормированной функцией уравнением
= N
то коэффициент N называется нормирующим множителем.
Для выражения вероятностных значений характеристик микрочастицы через волновую функцию квантовая
механика использует математический аппарат теории операторов. Оператором называется символ,
показывающий, что надо сделать с данной функцией, чтобы превратить ее в некую другую функцию, т.е.
оператор - это набор правил, ставящий в соответствие одной функции другую. Так, например, алгебраический
оператор ln показывает, что действие его на функцию f(x) сводится к нахождению функции F(x),
удовлетворяющей условию
f(x) = e
F(x)
Оператор частного дифференцирования
2
2
x
показывает, что функцию f(x,y...) нужно дважды
продифференцировать по x, полагая остальные переменные постоянными.
Квантовая механика утверждает, что каждой физической характеристике микрочастицы b соответствует
определенный оператор
B
. Так оператором координаты электрона является сама координата (
x
= x),
импульсу электрона отвечает оператор импульса
p
x
=-
i
x
, где i =
1
. Более сложным является
оператор полной энергии (оператор Гамильтона или гамильтониан):
U
m
2
2
2
- = H
(2-6)
где m - масса электрона, U - его потенциальная энергия,
2
(читается "набла квадрат") - оператор Лапласа
(лапласиан)
2
z
2
2
y
2
2
x
2
2
действие которого предполагает суммирование вторых частных производных, взятых по всем координатам
микрочастицы.
Чтобы найти вероятное значение того или иного свойства, нужно подействовать соответствующим
оператором на -функцию, результат умножить на -функцию и проинтегрировать полученное выражение по
всему объему:
b B
dV
(2-7)
Это утверждение имеет характер постулата, но без каких-либо исключений подтверждается опытом.
Набор волновых функций, необходимых для определения вероятностных значений свойств частицы,
находят, решая для нее основное уравнение квантовой механики (Э. Шредингер, 1926). Построим уравнение
Шредингера для электрона, находящегося в стационарном, то есть не изменяющемся с течением времени,
состоянии, которому отвечает стоячая волна де Бройля. Для этого воспользуемся уравнением стоячей волны и
принципом де Бройля.
Уравнение трехмерной стоячей волны имеет следующий вид:
15

2
2
A +
2
A = 0
(2-8)
где - длина волны, А - амплитуда. Для электрона с учетом физического смысла волновой функции в уравнении
(2-8) следует заменить A на , а вместо подставить ее значение из уравнения де Бройля ( = h/p), что приводит
к уравнению
2
2
2
0
h
p
или
2
2
2
0
p
Согласно (2-4)
р
2
=2mE
k
= 2m(E - U)
где E, E
k
и U - полная, кинетическая и потенциальная энергия электрона, откуда
2
2
2
0
m
E U
( )
(2-9)
Уравнение (2-9) - одна из форм уравнения Шредингера для стационарного состояния.
Перепишем уравнение (2-9) в следующей форме:
2
2
2m
U E
(2-10)
В соответствии с (2-5) левая часть уравнения (2-10) является результатом действия оператора полной энергии
(гамильтониана) на -функцию, откуда следует наиболее общее выражение уравнения Шредингера:
H E
(2-11)
Умножим правую и левую часть уравнения (2-11) на и проинтегрируем по всему объему
dVEΨΨHΨdV
2
Поскольку для стационарного состояния энергия постоянна, ее можно вынести за знак интеграла
E
H dV
dV
2
(2-12)
Однако, согласно (2-5), знаменатель правой части уравнения (2-12) равен единице, соответственно
E H dV
Тем самым доказана справедливость уравнения (2-7) применительно к полной энергии электрона.
2.4. Атом водорода. Одноэлектронные атомарные ионы
Атом водорода, состоящий из одного протона и одного электрона, является одной из немногих систем, для
которых уравнение Шредингера может быть решено строго.
Пусть в данный момент времени электрон находится на расстоянии r от ядра. Тогда сила, действующая на
электрон, составит
2
2
r
e
, а потенциальная энергия системы будут равна работе перемещения бесконечно
удаленного от ядра электрона на расстояние r:
r
e
dr
r
e
U
r
2
2
2
(2-13)
где е -заряд электрона. Подстановка (2-13) в (2-9) приводит к уравнению Шредингера для атома водорода
0)(
2
2
2
2
r
e
E
m
(2-14)
Решить это уравнение - значит найти набор функций , подстановка которых в (2-14) тождественно
превращает его в нуль.
Решение уравнения Шредингера - довольно сложная математическая задача. Для этого прежде всего
необходимо разделить переменные так, чтобы из уравнения (2-14) получить три независимых уравнения, каждое
из которых содержало бы только одну переменную. Для этого необходимо изменить систему координат и
16

перейти от прямоугольных координат к сферическим. В сферической системе координат положение точки в
пространстве задается расстоянием r от начала координат до данной точки и двумя углами - (угол широты) и
(угол долготы). Эти координаты, как видно из рис. 3, связаны с прямоугольными следующими соотношениями:
r
x
y
z
x = rsincos; y = rsinsin; z = rcos
Рис. 3. Прямоугольная и сферическая системы координат
В результате разделения переменных искомая волновая функция может быть найдена в виде произведения
трех функций, каждая из которых зависит только от одной переменной:
(r,,) = R(r)()() (2-15)
В уравнении (2-15) функция R(r) называется радиальной частью волновой функции, выражение ()() - ее
угловой частью.
Математическая сторона решения уравнения Шредингера выходит за рамки настоящего пособия;
ограничимся анализом тех следствий, к которым приводит решение этого уравнения.
1) Уравнение Шредингера имеет бесчисленное множество решений. Этот факт свидетельствует о том, что
для атома водорода возможно бесконечное число состояний, каждому из которых соответствует определенная
волновая функция. Иначе говоря, каждой электронной орбитали отвечает определенная волновая функция. В
силу этого квантовая механика под термином "электронная орбиталь" понимает не только область пространства,
для которой вероятность нахождения электрона отличается от нуля, но и саму волновую функцию,
описывающую поведение электрона в этом пространстве. Таким образом, если в химической литературе идет
речь о суммировании, вычитании, линейном комбинировании электронных орбиталей, в виду имеются
математические операции с уравнениями типа (2-15).
2) Уравнение Шредингера решается лишь для определенных значений полной энергии электрона. Это
следствие позволяет заключить, что энергии орбиталей меняются не монотонно, а дискретно, в результате чего
существует ряд энергетических уровней, на которых может находиться электрон атома водорода.
3) Выражения волновых функций включают ряд безразмерных параметров, значения которых изменяются
дискретно на единицу. Эти параметры называются квантовыми числами. Квантовые числа обеспечивают
квантование характеристик электрона, сообщая им дискретный характер.
Для описания состояния электрона необходимо столько квантовых чисел, сколько степеней свободы имеет
электрон. Поступательное движение в трехмерном пространстве, описываемое уравнением Шредингера,
характеризуется тремя степенями свободы, соответственно чему в уравнение (2-15) входят три квантовые числа:
главное, орбитальное и магнитное. Охарактеризуем каждое из этих чисел.
1. Главное квантовое число (n). Изменяется дискретно, принимая значения 1,2,3.... Главное квантовое
число характеризует прежде всего энергетический уровень электрона, выражаемый уравнением:
22
4
2
1
n
me
E
(2-16)
Поскольку масса (m) и заряд электрона постоянны, энергия последнего зависит только от квантового числа. Как
следует из (2-16), максимальное значение Е соответствует n = и равно нулю. Эта энергия отвечает удалению
электрона на бесконечно большое расстояние от ядра, т.е. ионизации атома водорода. Все остальные
разрешенные значения энергии отрицательны; минимальное из них составляет
E
me
1
2
4
2
= -1,3110
3
кДж/моль
Главное квантовое число характеризует также размеры орбитали. Совершенно очевидно, что орбиталь не
имеет строгих размеров в обычном понимании этого слова, так как электрон с разной вероятностью может
находиться в любой точке пространства. Под размерами орбитали в квантовой механике понимают
определенную вероятностную характеристику атома. Поместим ядро атома в центр координат, разобьем
окружающее его пространство на множество тончайших концентрических сферических слоев. Объем такого
слоя, отстоящего от ядра на расстояние r , будет равен 4r
2
dr, где dr - толщина слоя. Тогда в соответствии с
физическим смыслом квадрата волновой функции вероятность нахождения электрона в таком слое составит
17

dW = 4r
2
2
dr
Если построить кривую зависимости 4r
2
2
от r , то мы получим график функции радиального распределения
вероятности. Примеры таких кривых приведены на рис. 2. Эти кривые имеют один или несколько максимумов,
отвечающих расстояниям, на которых электрон находится наиболее часто. Чем выше максимум, тем больше
вероятность появления электрона на отвечающем этому максимуму расстоянии от ядра. Если на кривой 4r
2
2
= f(r) максимумов несколько, то самый высокий из них будет расположен тем дальше от ядра, чем больше
значение главного квантового числа.
2. Орбитальное квантовое число (). Для заданного значения n принимает целочисленные значения от 0 до
(n-1). Значение обозначается буквами в следующем порядке
0 1 2 3 4 5
Обозначение s p d f g h
Соответственно орбитали, для которых = 0 называются s-орбиталями, = 1 - р-орбиталями и т.д.
Орбитальное квантовое число характеризует энергетические подуровни атома, включающие орбитали с
одинаковыми значениями n и . Сколько значений принимает в пределах заданного значения n, столько
подуровней включает данный энергетический уровень. Так, например, второй энергетический уровень, для
которого n = 2, а принимает значения 0 и 1, имеет два подуровня, обозначаемые символами 2s и 2p.
Заметим, что для атома водорода подуровни одного уровня имеют одинаковую энергию, что следует из
уравнения (2-16), в случае многоэлектронных атомов, как будет показано ниже, подуровни с одинаковыми
значениями n отвечают разным энергиям.
От орбитального квантового числа зависят также значения, которые может принимать орбитальный момент
импульса электрона. Орбитальным моментом импульса называется векторное произведение радиус-вектора и
импульса электрона:
M = [r p]
Как всякий вектор, момент импульса характеризуется абсолютной величиной (модулем M
) и направлением,
определяемым проекциями M
на координатные оси. Орбитальное квантовое число квантует значения M
в
соответствии с уравнением
M ( 1)
Так, для s-подуровней модуль момента импульса равен нулю, для всех р-подуровней -
2
и т.д.
Орбитальное квантовое число определяет форму граничной поверхности орбитали. Так, все s-орбитали
имеют сферическую форму, р-орбитали - форму гантели (объемной восьмерки); форма d-орбиталей - либо
объемная четырехлепестковая розетка, либо гантель в кольце. Примеры формы орбиталей, отвечающих
различным значениям , приведены на рис. 1.
Главное и орбитальное квантовые числа совместно обуславливают форму кривой радиальной вероятности
для данного подуровня: число максимумов на этих кривых равно разности n-. Например, для подуровня 1s (n =
1, = 0) кривая радиальной вероятности имеет один максимум, для подуровня 2s (n = 2, = 0) - два максимума,
для подуровня 2p (n = 2, = 1) - один максимум и т.д. (рис. 2).
3. Магнитное квантовое число (m
). В пределах заданного значения магнитное квантовое число принимает
значения 0, 1, 2, 3... . Это квантовое число определяет положение вектора
M
в пространстве, квантуя
проекцию вектора на одну из координатных осей, например, на ось z:
M
z
=
m
Определению проекций
M
на другие координатные оси препятствует принцип неопределенности, так как, если
бы это было возможно, было бы установлено точное значение момента импульса электрона.
Характеризуя направление орбитального момента импульса, магнитное квантовое число тем самым
определяет ориентацию электронной орбитали в пространстве. Сколько значений принимает m
для заданного
значения , столько орбиталей, по-разному ориентированных в пространстве, возможно для данного подуровня
(рис. 1). Так, для s-подуровня m
принимает одно значение (m
= 0), соответственно чему s-орбиталь может быть
ориентирована в пространстве одним способом, а s-подуровень включает лишь одну орбиталь. В случае р-
подуровня m
l
имеет три значения (0, 1) и три р-орбитали этого подуровня ориентируются в пространстве тремя
разными способами: одна из них вытянута по оси x (орбиталь p
x
), другая по оси у (орбиталь p
y
), третья по оси z
(орбиталь p
z
) (рис. 1).
d-Подуровень включает пять орбиталей (m
= 0, 1, 2), ориентированных относительно координатных осей
пятью различными способами: орбиталь
2
z
d
представляет собой вытянутую по оси z гантель, продетую в
кольцо вращения (тороид) (рис. 1). Орбиталь
d
x y
2 2
- четырехлепестковая розетка, ориентированная по осям x и
y. Орбитали d
xy
, d
xz
, d
yz
имеют такую же форму, но ориентированы по биссектрисам соответствующих
координатных углов. Знаками (+) и (-) на рис. 1 указан математический знак волновой функции для разных
областей пространства.
Орбитали одного уровня, отличающиеся значениями m
, имеют одинаковые энергии. Число таких орбиталей
определяет степень вырождения подуровня. Так, s-подуровень не вырожден, р-подуровень трехкратно
18
вырожден, степень вырождения для d- и f-подуровней равна соответственно пяти и семи. В общем случае
степень вырождения определяется следующей формулой:
С.В. = 2 + 1 (2-17)
При помещении атома в электрическое или магнитное поле, энергии орбиталей с одинаковыми значениями , но
разными значениями m
становятся неодинаковыми, так как эти орбитали по-разному ориентированы
относительно направления поля. Происходит снятие вырождения, соответственно чему линии в атомном спектре
расщепляются.
Квантовые числа n, и m
квантуют физические характеристики электрона, связанные с его поступательным
движением. Однако электрон атома водорода, кроме орбитального момента импульса, имеет еще и собственный
момент импульса (спин), связанный с квантово-механическим аналогом вращательного движения, что
обеспечивает четвертую степень свободы электрона. Как указывалось выше, для квантования орбитального
момента импульса необходимы два квантовых числа ( и m
); аналогично для квантования собственного
момента импульса так же нужны два квантовых числа - спиновое (s), квантующее модуль момента (M
S
), и
магнитное спиновое (m
S
), квантующее направление вектора
S
M
. Экспериментально установлено, что в
сильных электрических и магнитных полях любая орбиталь проявляет свойства двух кратно вырожденной. Это
явление связано с наличием у электрона спина (Уленбек и Гоудсмит, 1925). Воспользовавшись уравнением (2-
17), имеем:
С.В. = 2s + 1; s = 1/2
Таким образом, квантовое число s является полуцелым и одинаково для всех электронов. Проекция
собственного момента импульса на направление магнитного поля имеет два значения, соответственно чему
магнитное спиновое квантовое число принимает значения +1/2 и -1/2. Найденные значения s и m
S
позволяют
проквантовать характеристики собственного момента импульса электрона:
M s s
S
( )1
;
M
S
Z
1
2
Четыре квантовые числа n, , m
и m
s
дают полную характеристику состояния электрона в атоме водорода.
Уравнение (2-14) может быть использовано для расчета волновых функций других одноэлектронных частиц
типа ионов He
+
, Li
2+
и т.д. В этом случае в уравнении (2-14) следует заменить величину e
2
/r на e
2
z/r, где z- заряд
ядра соответствующего атома. Некоторые волновые функции водородоподобных атомов приведены в табл. 3.
Чтобы перейти от них к волновым функциям атома водорода достаточно принять z равным единице.
Уравнение энергетических уровней для одноэлектронных частиц имеет вид
E
me z
n
1
2
4 2
2 2
(2-18)
Рассмотренное выше уравнение (2-16) является частным случаем уравнения (2-18).
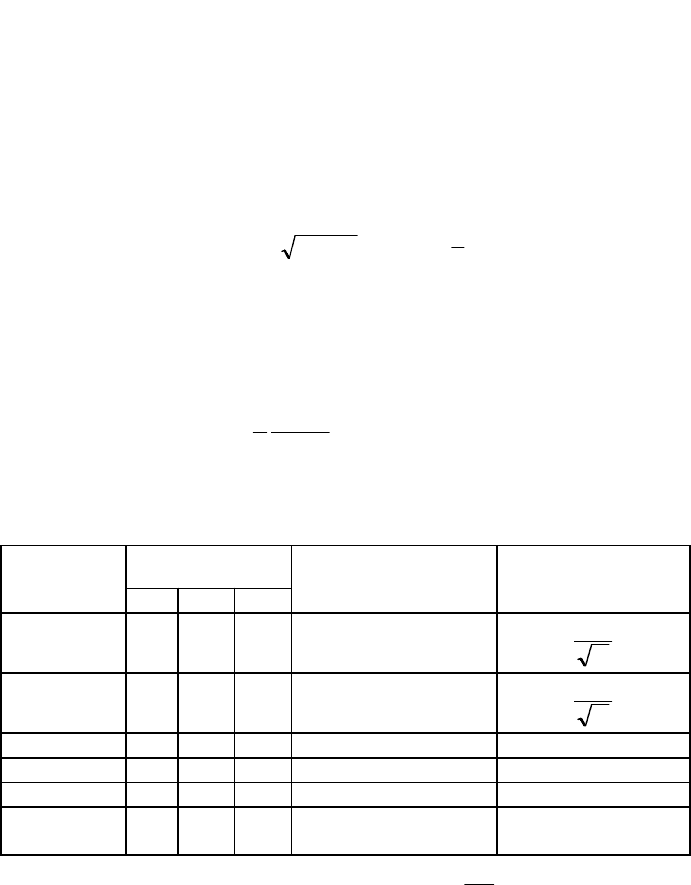
Таблица 3
Уравнения некоторых волновых функций
Орбитали
Квантовые
числа
Радиальная
функция Угловая функция
m
m
1s 1 0 0 2(z/a
0
)
3/2
e
-
/2
2
2s 2 0 0 (z/2a
0
)
3/2
(2-)e
-
/2
2
2p
x
2 1 0 (24)
-1/2
(z/a
0
)
3/2
e
-
/2
2
-1
3
1/2
-1/2
cos
2p
y
2 1 1 (24)
-1/2
(z/a
0
)
3/2
e
-
/2
2
-1
3
1/2
-1/2
sincos
2p
z
2 1 -1 (24)
-1/2
(z/a
0
)
3/2
e
-
/2
2
-1
3
1/2
-1/2
sinsin
3s 3 0 0 281
-1
9
-1/2
(z/a
0
)
3/2
(27-18+2
2
)e
-
/3
2()
-1
z - заряд ядра, а
0
= 52,9 пм, =
zr
a
0
2.5. Многоэлектронные атомы
В принципе уравнение Шредингера может быть применено для описания любого многоэлектронного атома.
Для этого необходимо соответствующим образом преобразовать уравнение (2-9): учесть координаты всех
электронов атома, подставить соответствующее выражение для потенциальной энергии. Решение такого
уравнения должно дать набор волновых функций для данного атома, позволяющих по уравнению (2-7)
рассчитать значения физических характеристик системы. Однако практически уравнение Шредингера не может
быть строго решено даже для двухэлектронной системы. Так, например, для атома гелия уравнение (2-9) примет
вид:
19

0)
22
(
2
12
2
2
2
1
2
2
2
2
2
1
r
e
r
e
r
e
E
m
где
2
1
и
2
2
- операторы Лапласа для первого и второго электронов, отстоящих от ядра на расстоянии r
1
и r
2
,
r
12
расстояние между этими электронами. Разделить переменные в полученном уравнении невозможно, в силу
чего оно не может быть решено строго. Тем не менее современная вычислительная техника позволяет
вычислять с достаточно высокой степенью точности приближенные значения свойств многоэлектронного атома.
Одним из приемов, используемых для подобных расчетов, является так называемый метод самосогласованного
поля. Для многоэлектронного атома задается набор грубо приближенных и в значительной мере произвольных
волновых функций, на основании которых вычисляется потенциальная энергия системы. Затем выбирают один
из электронов и вычисляют для него волновую функцию, отвечающую движению электрона в усредненном поле,
создаваемым ядром и остальными электронами. Используя найденное решение волнового уравнения для
первого электрона, вносят коррективы в усредненное поле, которое затем используется для вычисления
волновой функции второго электрона и т.д. Волновые функции электронов последовательно улучшаются до тех
пор, пока волновые функции в n-наборе и значения физических характеристик атома, рассчитанные с их
помощью, практически совпадут с функциями в (n-1)-ом наборе и с теми результатами, к которым использование
этих функций приводит. Найденные волновые функции тем лучше, чем меньше энергии, им отвечающие.
Подобные расчеты имеют определенную практическую ценность, однако их теоретическую значимость не стоит
переоценивать, так как эти приемы по существу являются методом "черного ящика". Поэтому при описании
многоэлектронных атомов широко используются менее строгие, но более наглядные подходы, которые будучи
основаны на определенных допущениях, тем не менее приводят к результатам, удовлетворительно
согласующимся с экспериментом. Среди таких подходов весьма результативной и простой является концепция
водородного (одноэлектронного) приближения, которая может быть сведена к следующим положениям:
1. Электронную оболочку любого многоэлектронного атома можно описать, используя те же квантовые числа
и тот же набор волновых функций, что и для атома водорода.
2. На энергетических уровнях и подуровнях многоэлектронного атома распределяются несколько электронов,
взаимодействие которых должно быть учтено. Электроны одного уровня образуют электронный слой.
Электронные слои обозначаются буквами K (n = 1), L (n = 2), M (n = 3) и т.д.
3. В невозбужденных атомах электроны заполняют орбитали в порядке возрастания их энергии (принцип
минимальной энергии).
Концепция водородного приближения позволяет построить электронные формулы (электронные
конфигурации) атомов, отражающие распределение электронов по энергетическим уровням и подуровням. При
составлении электронной формулы атома цифрами указывают значения главного квантового числа, буквой -
типы подуровней, а верхним правым индексом - число электронов на подуровне.
Чтобы составить электронную формулу, необходимо знать максимальное число электронов, удерживаемых
на том или ином уровне или подуровне (емкость уровня или подуровня), и последовательность заполнения
электронами уровней, обеспечивающую минимальную энергию системы. Вопрос о емкости электронных
орбиталей, энергетических уровней и подуровней позволяет решить принцип Паули (1925), которому
подчиняются многоэлектронные атомы:
В любой многоэлектронной системе не может быть двух электронов, с одинаковым набором всех
квантовых чисел.
Как следует из раздела 2.4., каждая орбиталь характеризуется лишь ей присущим набором главного,
орбитального и магнитного квантовых чисел (табл. 3.) Например, орбитали 2s соответствуют квантовые числа n
= 2, = 0, m
= 0. Если изменить хотя бы одно из этих чисел, приняв, например, орбитальное число равным 1, то
мы получим какую-то иную орбиталь (в данном случае 2p
z
). Таким образом, электроны, заполняющие ту или
иную орбиталь, могут отличаться лишь магнитным спиновым числом. Поскольку m
s
принимает лишь два
значения, число электронов, расположенных на одной орбитали, не может быть больше двух.
Число орбиталей энергетического подуровня, как было показано в разделе 2.4, равно числу значений,
принимаемых магнитным квантовым числом для данного подуровня, т.е. (2 + 1). Отсюда максимальное число
электронов, заполняющих подуровень, составит 2(2 + 1). Так, любой s-подуровень ( = 0, m
= 0) может
содержать не более 2 электронов, р-подуровень ( = 0, m
= -1,0,+1) - не более 6 электронов, d-подуровень ( = 2,
m
= -2, -1, 0, +1, +2) - не более 10 электронов.
Чтобы определить емкость энергетического уровня, достаточно установить, какие подуровни включает
данный уровень и удвоить сумму орбиталей этих подуровней. Например, первый энергетический уровень (n = 1,
= 0) состоит из одного подуровня 1s, в результате чего число электронов на нем не может быть больше двух.
Второй энергетический уровень (n = 2, = 0,1) включает 2s-подуровень (1 орбиталь) и 2р-подуровень (3
орбитали), так что его емкость равна восьми. Аналогично третий уровень может содержать до 18, а четвертый -
до 32 электронов. В общем случае максимальное число электронов энергетического уровня с главным
квантовым числом n равно 2n
2
.
Рассмотрим далее, в каком порядке орбитали заполняются электронами. Для этого необходимо установить
последовательность возрастания энергии подуровней многоэлектронных атомов. Покажем, что для подобных
атомов энергия подуровня зависит не только от главного, но и от орбитального квантового числа.
Как уже отмечалось, в многоэлектронном атоме имеет место межэлектронное отталкивание. Это
взаимодействие является причиной двух эффектов, влияющих на распределение электронов в атоме.
1. Эффект экранирования ядра
20
