Гук Ю.Б. Теория надежности. Введение: учеб. пособие
Подождите немного. Документ загружается.

81
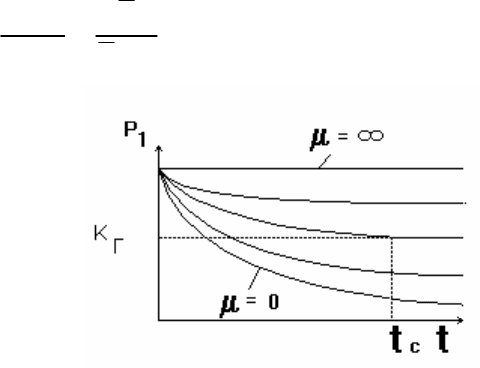
При достаточно большом t (t → ∞) процесс переходов
устанавливается, и вероятность P
1
(t) перестает зависеть от времени
(рис. 4.13):
1
()
Г
PK
µΤ
∞= = =
λ+µ Τ+τ
.
Рис. 4.13. Вероятности работоспособного состояния при различных
интенсивностях восстановления
Величина P
1
(∞) и есть оценка коэффициента готовности K
Г
.
Следует отметить, что при отсутствии резервирования
восстановление повышает надежность только в отношении
готовности, вероятность безотказной работы при этом не
увеличивается, а определяется только интенсивностью (частотой)
отказов λ.
При последовательном соединении элементов интенсивность
отказов системы может быть очень велика. Среднее время
восстановления будет определяться как математическое ожидание
времени восстановления на множестве
отказов всех элементов, а
следовательно, оно будет зависеть не только от времени
восстановления элементов, но и от вероятности отказов этих
элементов.
В системе с однократным резервированием (дублированием)
содержится два элемента. При отказе одного из них система остается
работоспособной, отказавший элемент восстанавливается. Если за
82
время восстановления одного элемента второй не отказывает, то
опасный режим проходит без последствий. Если же за время
восстановления отказавшего элемента отказывает второй, то система
теряет работоспособность до восстановления одного из отказавших
элементов.
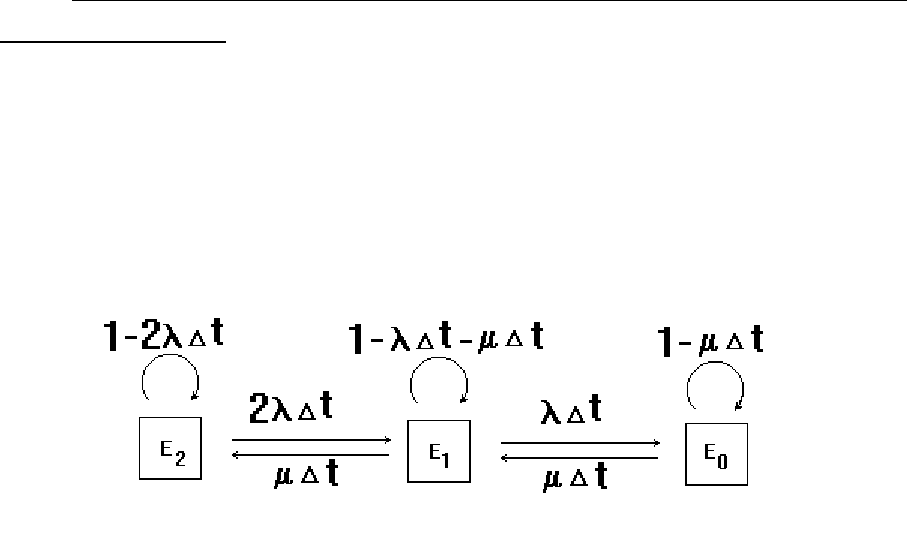
При постоянном резервировании и ограниченном
восстановлении (восстанавливаться может только один элемент)
система может находиться в трех состояниях: E
2
– работоспособны
оба элемента; E
1
– работоспособен только один из элементов; E
0
– оба
элемента неработоспособны. Граф переходов из состояния в
состояние с обозначением вероятностей переходов за время ∆t
изображен на рис. 4.14.
Рис. 4.14. Модель надежности дублированной системы с постоянным
резервированием и ограниченным восстановлением
Дифференциальные уравнения для вероятностей состояний –
() ()
(
)
() () ( ) () ()
() () ()
221
12 10
010
2;
2;
Pt Pt Pt
Pt P t Pt P t
Pt Pt Pt
′
=− λ +
µ
′
= λ − λ+µ +µ
′
=λ −µ
решаются с помощью преобразования Лапласа при начальных
условиях
P
2
(0) = 1, P
1
(0) = 0, P
0
(0) = 0
и при условии
83
P
2
(t) + P
1
(t) + P
0
(t) = 1 (полная группа событий).
Решение имеет вид
()
()
2
2112
0
2
2
2
exp exp
2
1
4
SStSSt
Pt
⎛⎞
−
λ
⎜⎟
=+
⎜⎟
λ+µ +λ
λ+λµ
⎝⎠
,
где
()
2
1,2
0,5 3 2 4 .S =− − λ+
µ
λ+λ
µ
m
Вероятность застать систему в работоспособном состоянии
P(t) = 1 – P
0
(t).
При достаточно большом t (t → ∞) процесс переходов
стабилизируется и P(t) перестает зависеть от времени
()
()
2
2
2
2
1
Г
K
λ
Ρ∞= − =
λ+µ +λ
.
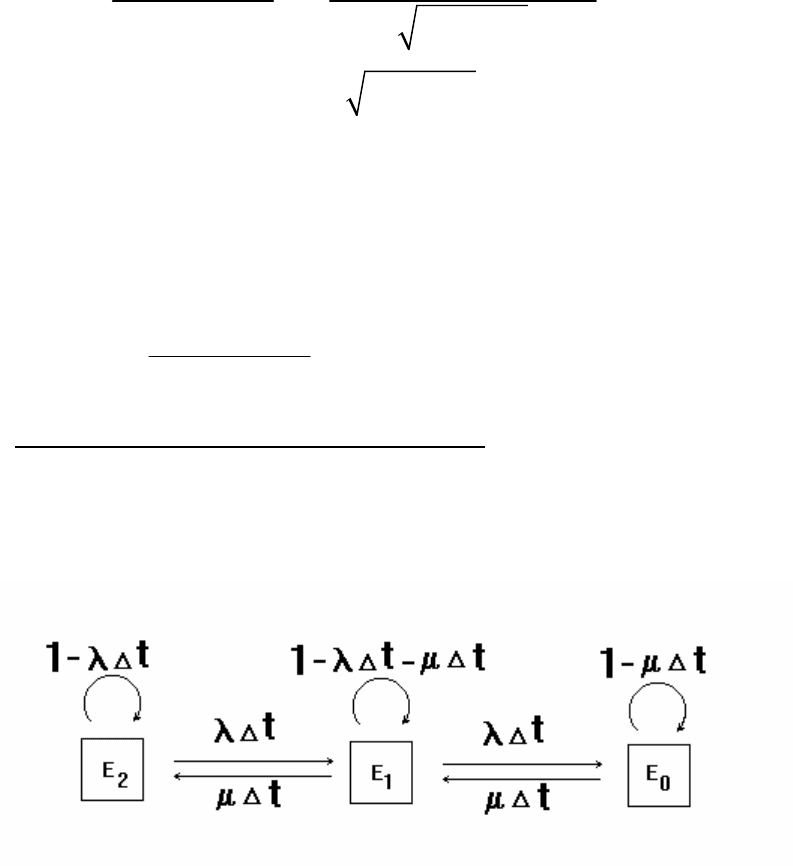
При резервировании замещением
(резервный элемент может
отказать только после того, как его включили вместо отказавшего
основного) и ограниченном восстановлении граф переходов примет
вид, представленный на рис. 4.15.
Рис. 4.15. Модель надежности дублированной системы с
резервированием замещением и ограниченным восстановлением
Дифференциальные уравнения для вероятностей состояний,
соответствующие этому графу
84
() () ()
() () ( ) () ()
() () ()
221
12 10
010
;
;
.
Pt Pt Pt
Pt P t Pt P t
Pt Pt Pt
′
=−λ +µ
′
=λ − λ+µ +µ
′
=λ −µ
При тех же начальных условиях решение для P
0
(t)
()
()
2
2112
0
2
exp exp
1,
2
SStSSt
Pt
⎛⎞
−
λ
=+
⎜⎟
⎜⎟
λµ
λ+µ +λµ
⎝⎠
где
(
)
1,2
.S =− λ+µ λµm
Вероятность застать систему в одном из работоспособных
состояний
P(t) = 1 – P
0
(t), а при t → ∞
()
()
2
2
1
Г
PK
λ
∞=− =
λ+µ +λµ
.
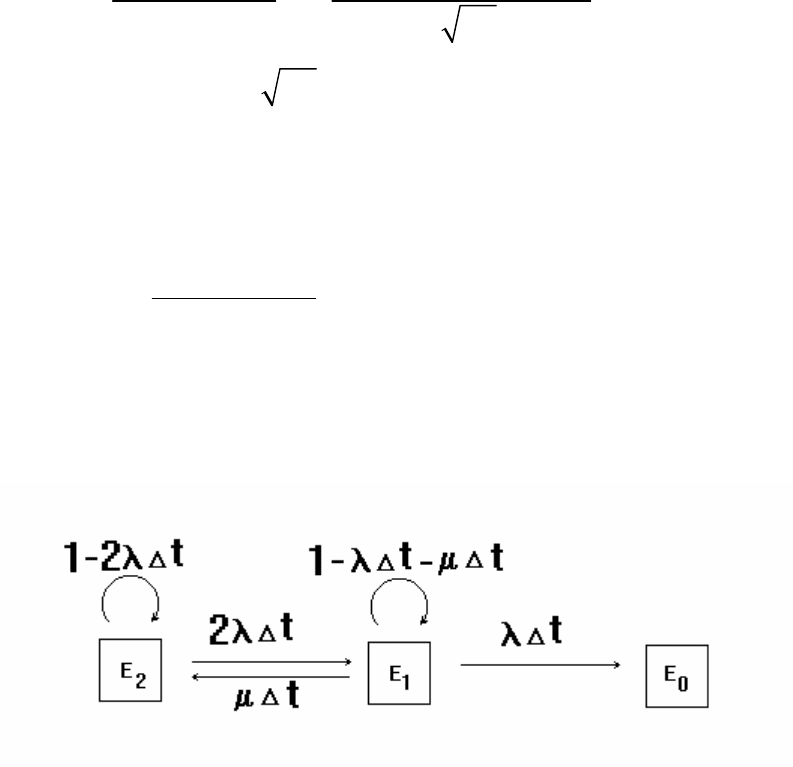
Для определения вероятности безотказной работы на расчетное
время граф переходов следует изменить (рис. 4.16 для постоянного
резервирования).
Рис. 4.16. Модель надежности дублированной системы с постоянным
резервированием для определения вероятности безотказной работы за
расчетное время
При начальных условиях P
2
(0) = 1, P
1
(0) = 0, P
0
(0) = 0 получим
решение P(t) = exp(– t/Y),
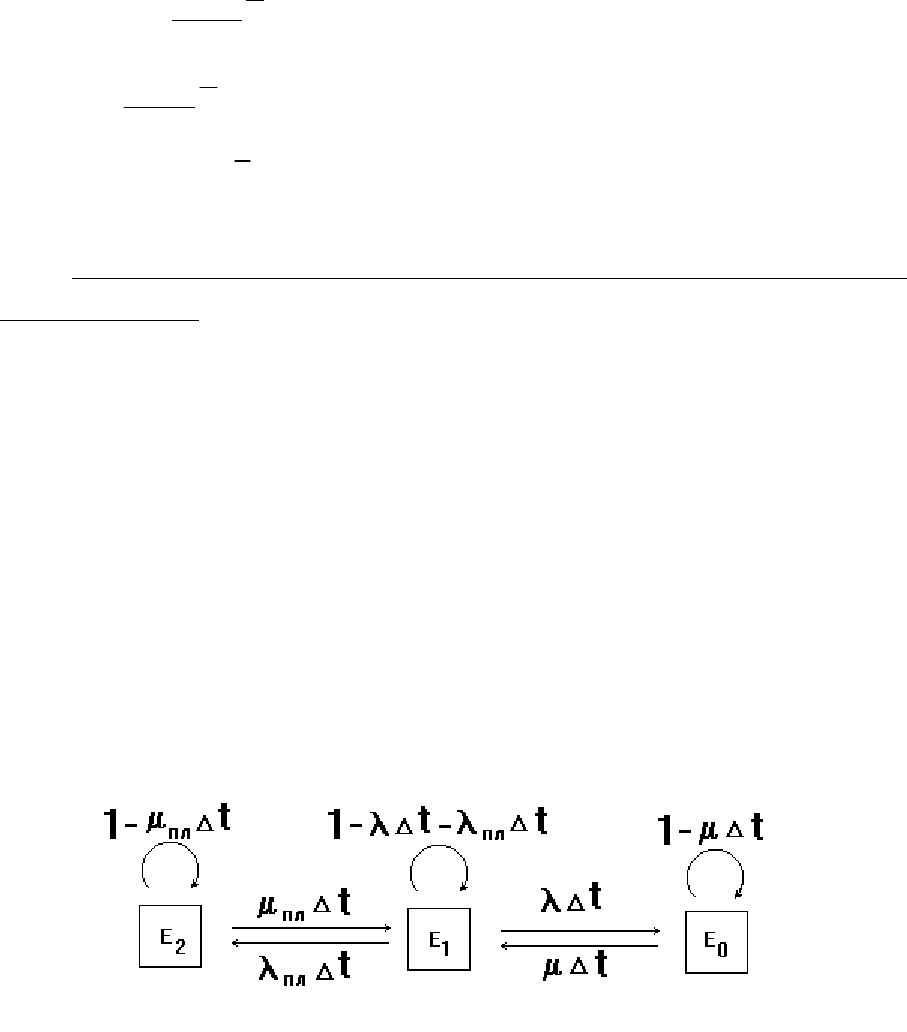
85
где
13
2
YT
+ρ
=
ρ
для постоянного резервирования;
12
YT
+ρ
=
ρ
для резервирования замещением,
//,Tρ=λ µ=τ
1/ .τ=
µ
Модель надежности элемента с восстановлением и
профилактикой
Установка с профилактикой и восстановлением, состоящая из
одного элемента, в любой момент времени может находиться в одном
из трех состояний: E
1
– работоспособное состояние; E
0
– аварийный
простой и восстановление, E
2
– плановый простой в
профилактическом обслуживании или ремонте. Граф переходов из
состояния в состояние для такой установки изображен на рис. 4.17,
где λ и λ
пл
– интенсивность аварийных и плановых отключений,
переводящих установку в состояние E
0
или E
2
; µ, µ
пл
– интенсивность
восстановления и планового ремонта, переводящих установку в
состояние E
1
.
Рис. 4.17. Модель надежности объекта с восстановлением и
профилактикой
Система дифференциальных уравнений для вероятностей
состояний, отвечающая этому графу

86
() ()
(
)
(
)
() () ()
() () ()
1 пл 10пл 2
010
2 пл 1 пл 2
() ;
;
.
Pt Pt P t P t
Pt Pt Pt
Pt Pt Pt
′
=−λ+λ +µ +µ
′
=λ −µ
′
=λ −µ
Полагая, что в момент t = 0 элемент работоспособен:
P
1
(0) = 1, P
0
(0) = 0, P
2
(0) = 0,
P
1
(t) + P
2
(t) + P
0
(t) = 1,
c помощью преобразования Лапласа получаем
()
(
)
(
)
()
()
()
()
1 пл 1
пл
11
пл пл пл 11 2
2 пл 2
2
22 1
exp
exp ;
kk
Pt kt
kk k
kk
kt
kk k
µ
+µ+
µµ
=+ +
µµ + λµ + µλ +
µ+ µ +
+
−
()
(
)
()
()
()
пл 1
пл
01
пл пл пл 11 2
пл 2
2
22 1
exp
exp ;
k
Pt kt
kk k
k
kt
kk k
λ
µ+
λµ
=++
µµ + λµ + µλ +
λµ +
+
−
()
(
)
()
()
()
пл 1
пл
21
пл пл пл 11 2
пл 2
2
22 1
exp
exp ;
k
Pt kt
kk k
k
kt
kk k
λµ+
µλ
=++
µµ + λµ + µλ +
λµ+
+
−
(
)
()( )
1,2 пл пл
2
пл пл пл пл пл
0,5[
4].
k =−λ+λ+µ+µ±
± λ+λ +µ+µ − µµ +λµ +µλ
Когда влияние начальных условий "стирается", распределение
вероятностей в фиксированный момент времени становится таким же,
как в любой другой момент, устанавливается равновесный, или
стационарный режим с определенными вероятностями состояний.
Чем больше промежутки времени между отказами по сравнению со
временем восстановления, тем скорее установка войдет в
87
стационарный режим. Для элементов электроэнергетических систем
стационарный режим наступает уже при значениях t от одного месяца
до одного года.
Для стационарного режима
1
1 пл пл
(1 / / ) ;
Г
PK
−
=+λµ+λ µ =
()
()
1
0 пл пл ав
/1/ / ;Pq
−
=λµ +λµ+λ µ =
()( )
1
2 пл пл пл пл пл
/1/ /Pq
−
=λ µ +λµ+λ µ = .
Приближенно можно принимать q
ав
= λτ, q
пл
= λ
пл
τ
пл
.
Вероятность работоспособного состояния P
1
(t) не есть
вероятность безотказной работы P(t). Последняя определяется при
запрещенном переходе из одного состояния в другое:
E
0
→ E
1
, E
1
→ E
2
, E
2
→ E
1
,
т.е. при
пл пл
0µ=λ =µ = .
Тогда система уравнений для вероятностей
()
(
)
11
;Pt Pt
′
=−λ
()
(
)
1
;
o
Pt Pt
′
=λ
2
() 0Pt
′
=
.
Решая при тех же начальных условиях, получаем
() () ( )
1
exp .Pt Pt t==−λ
Для определения вероятности того, что элемент будет
восстановлен за время t, рассматриваем состояния E
1
и E
2
как
поглощение, т.е. считаем, что λ = λ
пл
= µ
пл
= 0. В этом случае система
уравнений запишется в виде
()
(
)
10
;Pt P t
′
=µ
() ()
00
;Pt Pt
′
=−µ
()
2
0.Pt
′
=
Решая при начальных условиях
P
1
(0) = 1, P
0
(0) = 0, P
2
(0) = 0,

88
находим
(
)
1
( ) 1 exp( )Pt Gt t==−−µ.
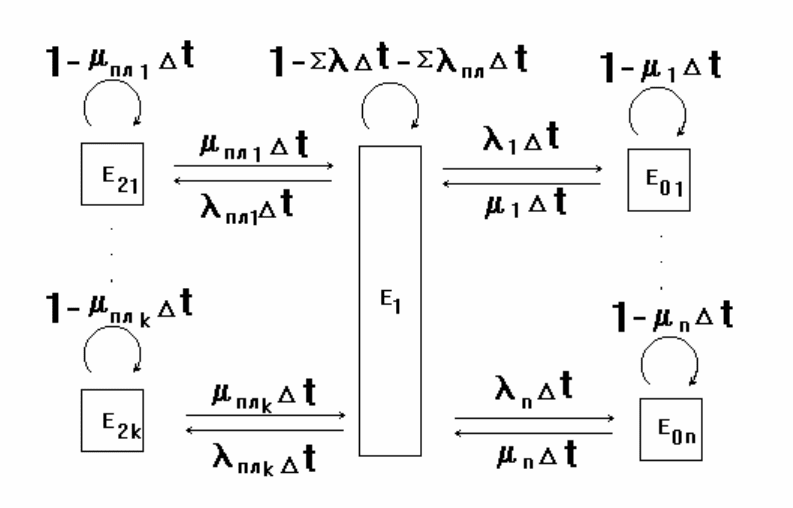
Последовательное соединение элементов
При последовательном соединении отказ любого элемента
приводит к отказу установки. На рис. 4.18 показан граф переходов из
состояния в состояние для такой системы. В общем случае k
≤ n, так
как возможно совмещение ремонтов элементов во времени. Система
дифференциальных уравнений, описывающих такой процесс
11 пл1 пл 10 2пл
11
() ( ... ... ) () () () ;
nk
nkiijj
ij
Pt Pt P t P t
==
′
=−λ + +λ +λ + +λ + µ + µ
∑∑
001
() () ()
iiii
Pt Pt Pt
′
=−µ +λ ;
2 пл 2 пл 1
() () ().
jjjj
Pt Pt Pt
′
=−µ +λ
Решая эту систему для стационарного режима при условиях
P
1
(0) = 1, P
0i
(0) = 0, P
2j
(0) = 0,
P
1
(t) + P
2
(t) + P
0
(t) = 1,
получаем
1
1 пл пл
11
(1 / / ) ;
nk
ii j j
Г
ij
PK
−
==
=+ λµ+ λ µ =
∑∑
0 ав
1
/;
n
Г ii
i
PK q
=
=λµ=
∑
2 пл пл пл
1
/.
k
Г jj
j
PK q
=
=λµ=
∑
89
Рис. 4.18. Модель надежности системы при последовательном
соединении элементов с восстановлением и профилактикой
Приближенно (с погрешностью менее 5%) для
электроэнергетических установок можно коэффициент простоя
определить как
ав
1
.
n
ii
i
q
=
=λτ
∑
Для определения вероятности безотказной работы система
уравнений составляется при условии, что состояния E
0i
поглощающие.
Полученное решение следующее
()
(
)
11
exp[ ( ... ) ] ,
n
Pt t Pt=−λ++λ= откуда
1
n
ci
i
=
λ
=λ
∑
.
Для определения вероятности восстановления за время t
составляется и решается система уравнений при условии, что
состояние E
1
поглощающее и что начало процесса отнесено к
моменту отказа. Тогда вероятность того, что система выйдет из
ремонта в течение времени t после отказа,
90
1
1
( ) ( ) ( / )[1 exp( )].
n
ic i
i
Gt P t t
=
==λλ−−µ
∑
Частота плановых ремонтов для последовательного соединения
пл ц ц
/,mTλ=
где m
ц
– число плановых ремонтов в течение ремонтного цикла,
Т
ц
– ремонтный цикл, или наименьший интервал времени, в
течение которого производится целое число ремонтов (текущих и
капитальных) каждого элемента. Длительность ремонтного цикла
определяется как наименьшее общее кратное периодичности
плановых ремонтов элементов:
пл пл
1/
ii
Т
=
λ . Среднее время одного
ремонта
ц
пл ц пл max
1
(1 / ) ,
m
j
j
m
=
τ= τ
∑
где τ
плjmax
– наибольшее время планового ремонта одного
элемента из отключаемых в j-м простое.
Коэффициент планового простоя
q
пл
= λ
пл
τ
пл
.
5. МЕТОДЫ РАСЧЕТА НАДЕЖНОСТИ
ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ УСТАНОВОК
5.1. Аналитический расчет надежности
электроснабжения
Аналитический метод применим для сетей с радиальной и
магистральной схемой питания потребителей [7]. Все элементы такой
схемы имеют последовательные и параллельные соединения.
Формулы для показателей надежности последовательного и
параллельного соединения дают возможность вычислять показатели
надежности эквивалентных элементов. Эквивалентирование
расчетной схемы позволяет оценить показатели надежности схемы
