Гук Ю.Б. Теория надежности. Введение: учеб. пособие
Подождите немного. Документ загружается.

11
выполнения заданных функций, называется отказом в работе (отказом
функционирования). Отказы бывают полные и частичные.
Сохраняемость – свойство объекта сохранять значения
показателей безотказности, долговечности и ремонтопригодности в
течение и после хранения и (или) транспортировки.
Устойчивоспособность – свойство объекта непрерывно
сохранять устойчивость в течение некоторого времени.
Режимная управляемость – свойство объекта поддерживать
нормальный режим посредством
управления.
Живучесть – свойство объекта противостоять возмущениям, не
допуская их каскадного развития с массовым нарушением питания
потребителей.
Безопасность – свойство объекта не допускать ситуации
опасные для людей и окружающей среды. Учитывая безусловную
важность этой составляющей, часто ее выделяют из понятия
надежности, говоря о надежности и безопасности объектов
энергетики, например, атомной электростанции или высоковольтной
установки.
Состояния, характеризующие надежность объектов
энергетики.
Работоспособное состояние – состояние объекта, при котором
он способен выполнять все или часть заданных функций в полном
или частичном объеме.
Неработоспособное состояние – состояние объекта, при
котором он не способен выполнять заданные функции.
Рабочее состояние – состояние объекта, при котором он
выполняет все или часть заданных функций в полном или частичном
объеме.
Нерабочее состояние – состояние объекта, при котором он не
выполняет все заданные функции.
12
Предельное состояние – состояние объекта, при котором его
дальнейшая эксплуатация должна быть прекращена из-за
неустранимого нарушения требований безопасности или
неустранимого снижения уровня работоспособности или
недопустимого снижения эффективности эксплуатации.
Резервное состояние – рабочее состояние объекта, при котором
он осуществляет резервирование других объектов.
Зависимый простой– нерабочее состояние объекта, возникшее
вследствие отключения других объектов или
проведения на них
работ, требующих отключения данного объекта, работоспособность
которого при этом не нарушается.
События, характеризующие надежность объектов
энергетики.
Отказ работоспособности – событие, заключающееся в
переходе объекта с одного уровня работоспособности на другой,
более низкий.
Отказ функционирования – событие, заключающееся в переходе
объекта с одного уровня функционирования на другой, более низкий.
Отказы объектов в энергетике классифицируются как полные и
частичные; внезапные и постепенные; независимые и зависимые;
устойчивые и cамоустраняющиеся.
У объектов, функционирующих не непрерывно во времени
различают:
Отказ срабатывания – отказ функционирования,
заключающийся в невыполнении объектом требуемого срабатывания.
Излишнее срабатывание – отказ функционирования,
заключающийся в срабатывании объекта при требовании
срабатывания других объектов и отсутствии требования срабатывания
данного объекта.
13
Ложное срабатывание – отказ функционирования,
заключающийся в срабатывании объекта при отсутствии требования
срабатывания данного и других объектов.
Авария – событие, заключающееся в переходе объекта с одного
уровня работоспособности или относительного уровня
функционирования на другой, существенно более низкий, с
серьезным нарушением режима работы объекта.
Восстановление – событие, заключающееся в повышении
уровня работоспособности объекта или
относительного уровня его
функционирования. Оно осуществляется в результате аварийного,
планового, внепланового ремонта и в ходе профилактического
обслуживания.
Средства обеспечения надежности объектов энергетики.
Резервирование – повышение надежности объекта введением
избыточности.
Резервирование бывает структурное, функциональное,
временное, информационное, постоянное, замещением. Резерв бывает
ремонтным, оперативным, аварийным, нагрузочным,
эксплуатационным.
Техническое обслуживание – выполнение работ для
поддержания исправности
или работоспособности объекта при
подготовке к использованию по назначению.
Ремонтом – выполнение работ для поддержания или
восстановления исправности или работоспособности объекта.
Исправное состояние – состояние объекта, при котором он
соответствует всем заданным нормативным требованиям. Контроль за
уровнем работоспособности осуществляется средствами технической
диагностики.

14
2. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
2.1. Множество
Общие понятия
Вероятность является свойством событий; события, в свою
очередь, представляются в виде множеств. Рассмотрим некоторые
понятия из теории множеств [3]. Множество – совокупность
элементов
A = [а
1
, а
2
, … , а
n
].
Если n = 0 – пустое множество, n = ∞ – бесконечное множество.
Если
i
α является элементом множества А, то
α
i
∈
A.
Соотношения между множествами:
Определяются наличием или отсутствием общих элементов. Для
двух множеств А и В существуют следующие возможности:
- А и В имеют общие элементы, но каждое из множеств имеет
также элементы, которые не принадлежат к другому множеству.
Множества пересекаются. На рис. 2.1, а представлена диаграмма
Эйлера-Венна для этого случая.
- А и В не имеют общих элементов, они не пересекаются
(рис. 2.1, б).
- множество А целиком включает в себя другое множество В
(рис. 2.1, в). Множество В является подмножеством А, В ⊂ А.
Операции с множествами:
а) Объединением двух множеств называют множество С,
которое содержит все элементы составляющих его множеств А и В
(рис. 2.2, а):
С = А U В или С = А + В.

15
AA
A
B
B
B
а) б) в)
Рис. 2.1. Диаграмма Эйлера-Венна для множеств А и В:
а) множества А и В имеют общие элементы;
б) множества А и В не имеют общие элементы;
в) множество А включает в себя подмножество В
б) Пересечением двух множеств называют множество С,
которое содержит все элементы , являющиеся общими для обоих
множеств А и В (рис. 2.2, б).
С = А I В или C = А·В или C =АВ.
Если А и В непересекающиеся множества, то А I В = 0.
в) Разностью А \ В двух множеств называют множество C,
состоящее из тех элементов множества А, которые не являются в то
же время элементами множества В (рис. 2.2 , в).
C = А \ В, тогда (А \ В) + В = А + В.
г) Дополнение. Если S – множество всех элементов для
рассматриваемой ситуации, а А – подмножество множества S, то
дополнением
A
множества А называют множество, состоящее из всех
тех элементов, которые не входят в А (рис. 2.3, а). Следовательно,
A
= S \ A или А U
A
= S и А I
A
= 0.

16
AAA
BBB
а) б) в)
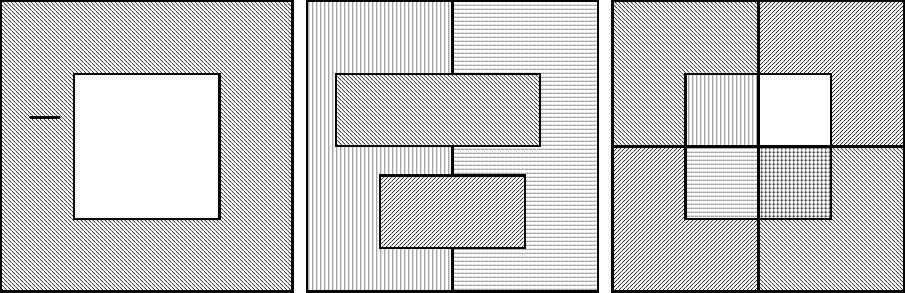
Рис. 2.2. Операции с множествами:
а) объединение множеств А и В;
б) пересечение множеств А и В;
в) разность множеств А и В.
С помощью этих операций можно построить целую алгебру
множеств:
АU (ВI С) = (АU В) I (АU С); A I (В U С) = (А I В) U (А I С);
A
BAB=UI
; ;
A
BAB=IU
(
)
;
A
BAB=IU
(
)
()
.
A
AB AB= IUI
2.2. События
Понятие события связывается с исходами многократно
повторяемых экспериментов. Каждое испытание в ходе эксперимента
приводит к некоторому исходу.
17
AA
S
A
H1 H2
H3 H4
C1 C2
A
B
а) б) в)
Рис. 2.3. Соотношения между событиями:
а) противоположные события;
б) совместные и несовместные события;
в) полная группа событий Н.
Множество всех возможных исходов составляет пространство
элементарных событий S. Событием С называют некоторое
подмножество S, включающее в себя все исходы, которые
удовлетворяют некоторому критерию или требованию. При каждом
испытании событие либо происходит, либо не происходит, в
соответствии с тем, где находится исход данного испытания: внутри
или вне множества исходов, составляющих событие.
Пример 2.1. Если бросаем 2 кубика, то пространство
элементарных событий можно представить в виде:
S = {1,1; 1,2; ...; 6,5; 6,6}.
Если событие С1 – сумма очков равная 8, то событие будет
состоять из следующих исходов.
С1 = {2,6; 3,5; 4,4}.
Если критерием события С2 является то, что на обоих кубиках
число очков должно быть одинаковым, то:
C2 = {1,1; 2,2; ...; 6,6}.
18
Операции над событиями аналогичны операциям над
множествами.
С1 I С2 = {4,4}; C1 U C2 = {1,1; 2,2; 2,6; 3,3; 3,5; 4,4; 5,5; 6,6}.
События могут быть: достоверными (в результате опыта
обязательно произойдет); невозможными (в результате опыта
заведомо не произойдет); случайными (в результате опыта может
либо произойти, либо не произойти), если будет соблюдена
определенная совокупность условий.
Пространство элементарных событий – достоверное событие
(U). Дополнение достоверного события есть невозможное событие (V)
(пустое множество). Если С1I С2 = V , то события являются
взаимоисключающими (несовместными), в противном случае –
совместными ( ≠ V ).
С1 и С2 (см. выше пример) совместные. Если определить
событие C3 , как состоящее в том, что сумма очков на двух кубиках
равна 7, то С2 и С3 – несовместные.
Противоположными событиями называют два несовместных
события, образующих полную группу случайных событий (см. рис.
2.3, а).
События Н
i
образуют полную группу, если в результате опыта
обязательно должно произойти одно из них (см. рис. 2.3, в).
Произведением нескольких событий называется событие,
состоящее в появлении всех этих событий. Логически произведение
событий отвечает операции "И" – и тот и другой, и т. д.
Суммой нескольких событий называется событие, состоящее в
появлении хотя бы одного из этих событий. Логически сумма
событий отвечает операции "ИЛИ" – или тот, или другой, или их
сочетания и т. д.
События в булевой алгебре трактуются как высказывания.
Булева алгебра – исчисление высказываний.
Значению “истина” соответствует цифра “1”, а “ложно” – “0”.

19
Функция, принимающая лишь два значения, называется
функцией алгебры логики (ФАЛ).
Логические операции это: отрицание (“НЕ”), умножение
(конъюнкция или “И”) и сложение (дизъюнкция или “ИЛИ”).
Отрицание высказывания
А обозначается как
A
(не А), умножение А
и В – как А ∧В и сложение А и В – как А∨В.
Таблица истинности представлена в табл. 2.1.
Таблица 2.1.
Таблица истинности для двух событий А и В
А В А ∧В А В А∨В А
A
0 0 0 0 0 0 1 0
0 1 0 0 1 1 0 1
1 0 0 1 0 1
1 1 1 1 1 1
2.3. Вероятность
Вероятность есть мера, связанная с событиями. Каждому
событию соответствует некоторое значение вероятности. Значения
вероятностей находятся в интервале от 0 до 1. Значение вероятности 1
соответствует достоверному событию, а 0 – невозможному событию.
Вероятность некоторого события А обозначается, как Р(А).
Аксиомы вероятности:
1) 0 ≤ Р(А) ≤ 1.
2) Р(S) = 1, Р(U) = 1 (вероятность достоверного события).
3) Для двух несовместных событий А и В
Р(АU В) = Р(А) + Р(В).
На основе этих аксиом строится вся теория вероятностей.
Вероятности противоположных событий связаны равенством
Р(
A
) = 1 – Р(А).
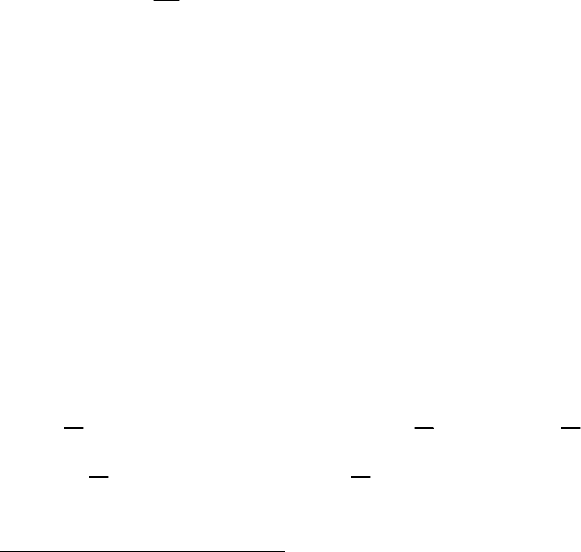
20
Вероятность невозможного события Р(V) = 0. Численные
значения вероятностей находятся на основе рассуждений (априорные
вероятности) или опыта (апостериорные вероятности).
Классическое определение вероятности (априорное): Если
результат опыта можно представить в виде полной группы событий,
которые попарно несовместны и равновозможны, то вероятность
события А равна отношению числа m благоприятствующих этому
событию исходов опыта к общему числу n всех возможных исходов,
т.е.
Р(А) = m/n.
Статистическое определение вероятности (апостериорное) или
иначе определение вероятности методом относительной частоты
Р(А) = m/n. Здесь m – число появления события А, n – количество
испытаний. Чем больше n , тем точнее результат.
()
lim
n
m
RA
n
→∞
= .
Вероятность можно трактовать как отношение площадей
событий, изображенных на диаграмме Эйлера-Венна. Например, на
рис. 2.3, а вероятность события А – Р(A) = A/S, где A – площадь на
диаграмме, отвечающая событию A, а S – площадь всей диаграммы,
отвечающая всему пространству элементарных событий.
Основные свойства
1) Р(U) = n/n = 1.
2) Р(V
) = 0/n = 0.
3) Р(А
U В) = Р(A) + Р(B), если A I B = V.
4) Р(
A
) = 1 – Р(A) , так как А U
A
= U, А I
A
= V,
Р(A
U
A
) = Р(U), Р(A) + Р(
A
) = 1 .
Условная вероятность
Пусть А и В зависимы, т.е. вероятность события А зависит от
того, появилось или не появилось событие В. В этом случае
вероятность является условной и обозначается как Р(А|В) или
