Гук Ю.Б. Теория надежности. Введение: учеб. пособие
Подождите немного. Документ загружается.


21
P
B
(A).Условной вероятностью называют вероятность события А,
вычисленную в предположении, что событие В уже наступило:
Р(А|В) = Р(А
I В)/Р(В).
Обратимся к рис. 2.3, б. Все пространство событий составляет
множества элементарных событий или С1, или С2, которые являются
несовместными. События, составляющие множество A и B, могут
происходить совместно с событиями множеств C1 или C2.
Приведенная диаграмма позволяет продемонстрировать понятие
условной вероятности. Вероятность события A при условии события
C1 есть отношение площади
, отвечающей пересечению событий A и
C1 к площади события C1.
Два события называются независимыми, если наступление
одного из них не изменяет вероятности второго:
Р(А|В) = Р(А).
Умножение вероятностей
Независимые события. Для двух независимых событий А и В:
Р(А
I В) = Р(АВ) = Р(А)·Р(В).
В общем случае Р(А) =
()
1
n
i
i
P
A
=
∏
, где
1
n
i
i
A
A
=
=
∏
.
Зависимые события. Для двух зависимых событий:
Р(АВ) = Р(А)Р(В|А).
В общем случае
21 312 12 1
() ( | )( | ) ( | )
nn
PA PA A PA AA PA AA A
−
=⋅⋅⋅⋅⋅⋅,
где
1
n
i
i
A
A
=
=
∏
.
Сложение вероятностей
Для двух совместных событий
А и В
Р(А U В) = Р(А) + Р(В) – Р(АВ).

22
а) б) в)
Рис. 2.4. К операциям с вероятностями:
а) к сложению вероятностей двух совместных событий;
б) к сложению вероятностей трех совместных событий;
в) к сложению вероятностей двух несовместных событий.
Для трех совместных событий
А, В и C:
Р(АU ВU C) = Р(А)+Р(В)+Р(C) – Р(АВ) – Р(AC) – Р(BC) + Р(ABC).
В общем случае:
() ( )
121
1 1 11 111
1
1
() ...
... ( 1)
nn nn nnn
ii ij ijk
ii iji ijikj
n
n
i
i
PA PA PAA PAAA
PA
−−−
== ==+ ==+=+
−
=
⎛⎞
=− + −
⎜⎟
⎝⎠
⎛⎞
+−
⎜⎟
⎝⎠
∑ ∑ ∑∑ ∑∑∑
∏
Для двух совместных и независимых событий:
Р(А U В) = Р(А) + Р(В) – Р(А)·Р(В).
Для двух совместных и зависимых событий:
Р(А U В) = Р(А) + Р(В) – Р(А)·Р(В|А).
Для несовместных событий:
Р(АU В) = Р(А) + Р(В).
В общем случае для несовместных событий:
11
().
nn
ii
ii
PA PA
==
⎛⎞
=
⎜⎟
⎝⎠
∑∑
Для противоположных событий:
Р(A) + Р(
A
) = 1.

23
1
() ( )
n
i
i
PA PA
=
=
∑
= 1, если А – полная группа событий.
Формула полной вероятности
Вероятность события
А, которое может наступить лишь при
условии появления одного из несовместных событий (гипотез)
H
1
, H
2
,
… ,
H
n
, образующих полную, равна сумме произведений вероятностей
каждого из этих событий на соответствующую условную вероятность
события А:
1
() ( )( | )
n
ii
i
PA PH PAH
=
=
∑
.
Доказательство формулы полной вероятности: согласно
условию, событие
А можно представить в виде несовместных
комбинаций
...
12
A
AA A
n
=+ ++
Η
ΗΗ
. Для i = 4 см. рис. 2.3.
По теореме сложения вероятностей несовместных событий
( ) ( ) ( ) ... ( ).
12
PA P A P A P A
n
=+ ++
ΗΗ Η
По теореме умножения зависимых событий
112 2
() ( )( | ) ( )( | ) ... ( )( | )
nn
PA PH PAH PH PAH PH PAH=+ ++
или
1
() ( )( | )
n
ii
i
PA PH PAH
=
=
∑
.
Формула Байеса
Следствием теоремы умножения и формулы полной
вероятности является теорема гипотез или формула Байеса. Имеем
полную группу несовместных гипотез H
1
, H
2
, … , H
n
. Вероятности
этих гипотез до опыта известны и равны, соответственно, P(H
1
),
P(H
2
), … , P(H
n
). Известны вероятности (| )
i
PAH . Проведен опыт, в
результате которого наблюдалось появление некоторого события А.
Определим вероятность событий H
i
после опыта. На основании
правила умножения имеем:

24
(
)
()
(
)
(
)
()
i
iii
PPPA AH|A=PHPA|H
H
= ,
откуда
()(| )
(|)
()
ii
i
PH PA H
PH A
PA
=
.
Используя формулу полной вероятности для Р(А), имеем:
1
()(| )
(|)
()(| )
ii
i
n
jj
j
PH PA H
PH A
PH PA H
=
=
∑
.
2.4. Случайные величины и их распределения
Рассмотрим многократно повторяющийся эксперимент.
Случайная величина является некоторой функцией исхода. Значения
случайной величины зависят от случайного исхода эксперимента.
Случайной называют величину, которая в результате испытания
примет одно и только одно возможное значение, наперед неизвестное
и зависящее от случайных причин, которые заранее не могут быть
учтены. Например, число родившихся мальчиков среди ста
новорожденных. Случайные величины могут быть дискретными или
непрерывными. Будем обозначать случайные величины прописными
буквами Х, Y, ... , а их возможные значения соответствующими
строчными буквами х, у, ... .
Х = {x
1
, x
2
, x
3
, ... };
Y = {y
1
, y
2
, y
3
, ... }.
Дискретной (ДСВ) называется случайная величина, которая
принимает отдельные, изолированные возможные значения с
определенными вероятностями. Число возможных значений может
быть конечным или бесконечным.
Непрерывной (НСВ) называется случайная величина, которая
может принимать все значения из некоторого конечного или
бесконечного промежутка. Число возможных значений – бесконечно.

25
Законы распределения вероятностей ДСВ
Дискретная случайная величина Х может быть задана рядом
распределения или функцией распределения (интегральным законом
распределения). Рядом распределения называется совокупность всех
возможных значений x
i
и соответствующих им вероятностей
p
i
= P(X = x
i
).
X
х
1
х
2
х
3
...
х
n
p
p
1
p
2
p
3
...
p
n
События X = x
1
, X = x
2
, ... , X = x
n
, образуют полную группу;
следовательно, сумма вероятностей этих событий равна единице:
p
1
+ p
2
+ … + p
n
= 1
или
1
1
n
i
i
p
=
=
∑
.
Графическое изображение ряда распределения называется
гистограммой (рис. 2.5) или полигоном (многоугольником)
распределения (рис. 2.6).
Функцией распределения (интегральным законом
распределения) случайной величины Х называется функция F(x),
равная вероятности Р(Х < х) того, что случайная величина будет
меньше произвольно выбранного значения х (действительного числа).
Функция F(x) вычисляется по формуле
F(x) = Р(
Х < x) =
i
i
xx
p
<
∑
,
p
i
= P(X = x
i
),
где суммирование ведется по всем значениям i, для которых х
i
< х.
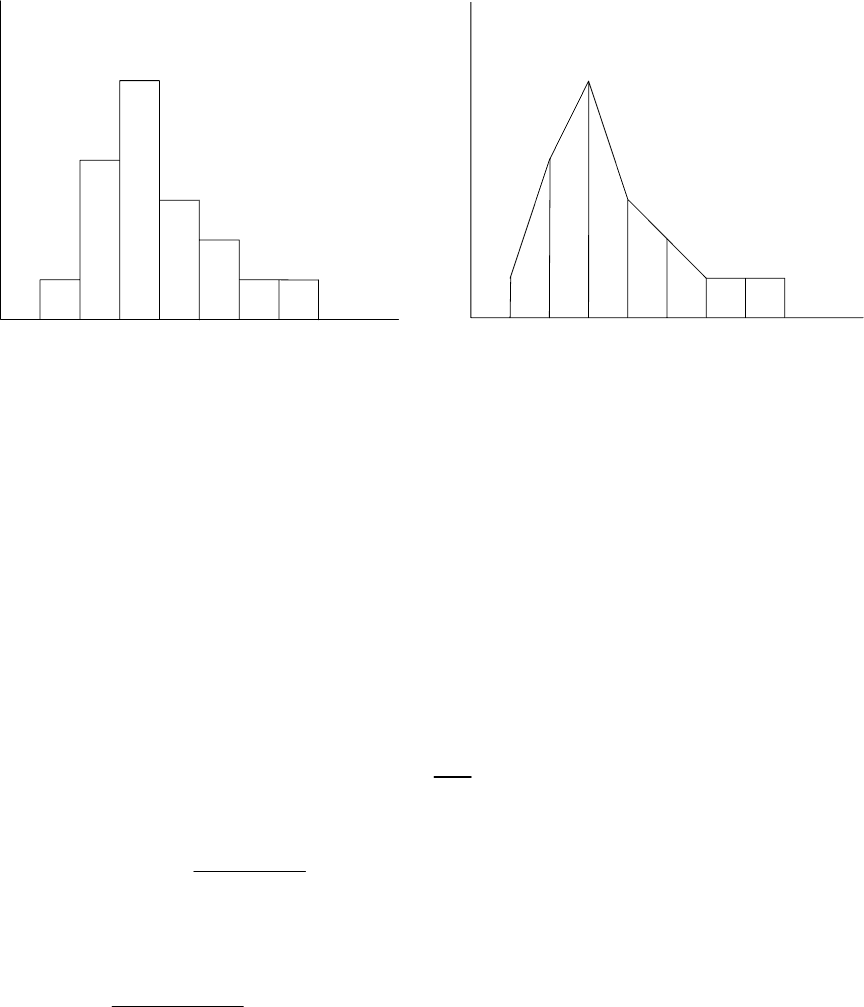
26
p
x
p
x
Рис. 2.5. Гистограмма
распределения
Рис. 2.6. Полигон
распределения
Пример 2.2. Из партии, содержащей 100 изделий, среди которых
имеется 10 дефектных, выбраны случайным образом пять изделий для
проверки их качества. Построить ряд распределений случайного
числа Х дефектных изделий, содержащихся в выборке.
Решение: В выборке число дефектных изделий может быть в
пределах от 0 до 5 включительно.
Х = {0, 1, 2, 3, 4, 5}
Вероятность
Р(Х = x
i
), где x
i
= 0,5 , равна
5
10 90
5
100
()
ii
x
x
i
CC
PX x
C
−
== .
Вычисление сочетаний производят по следующим формулам
()
!
,
!!
m
n
n
C
mn m
=
−
,
mnm
nn
CC
−
=
0
1,
n
C =
0! = 1.
C точностью до 0,001 получаем:

27
p
1
= P(X = 0) = 0,583;
p
2
= P(X = 1) = 0,340;
p
3
= P(X = 2) = 0,070;
p
4
= P(X = 3) = 0,007;
p
5
= p
6
= 0;
F(0) = 0,583;
F(1) = 0,923;
F(2) = 0,993;
F(3) = 1,0.
Законы распределения вероятностей НСВ
Задать непрерывное распределение в виде таблиц нельзя. Закон
распределения для непрерывной случайной величины задают в двух
видах. В виде функции распределения (интегральный закон
распределения)
F(х) и плотности вероятностей распределения
(дифференциальный закон распределения)
f(х).
I.
F(x) = P(X < x) – зависимость вероятности Р(Х < x) от х.
Функция распределения
F(x) имеет следующие основные свойства:
1)
Р(а < X < b) = F(b) – F(a);
2)
F(x
1
) < F(x
2
), если x
1
< x
2
;
3)
lim ( )
x
F
x
→∞
= 1;
4)
lim ( )
x
Fx
→−∞
= 0.
II. f(x) =
0
()
lim
x
Px X x x
x
∆→
<≤+∆
∆
=
dF
x
dx
()
.
Функция распределения вероятностей и плотности
распределения вероятностей случайной величины связаны
соотношением:
() ()
x
F
xfxdx
−∞
=
∫
.
Функция f(x) обладает следующими свойствами:

28
1) f(x) ≥ 0;
2) f(x) =
()dF x
dx
;
3)
∞
−∞
∫
f(x)dx = 1;
4) P(a ≤ X < b) =
()
b
a
f
xdx
∫
.
Числовые характеристики распределений
Числовые характеристики вычисляются в предположении, что
известны функции распределения, т.е. для дискретной случайной
величины Х – р(х), а для непрерывной случайной величины Х – f(x).
Закон распределения полностью характеризует случайную величину,
но для решения многих задач достаточно использовать числовые
характеристики случайной величины. К числу важных числовых
характеристик относятся математическое
ожидание, дисперсия и
среднеквадратическое отклонение.
Математическим ожиданием называют сумму произведений
всех ее возможных значений на вероятности этих значений. Для
дискретной случайной величины Х
М(Х) =
1
n
ii
i
p
x
=
∑
.
Для непрерывной случайной величины Х:
М(Х) =
∞
−∞
∫
x f(x)dx.
Дисперсия D(X) и среднеквадратическое отклонение
()DX
распределения характеризуют рассеяние случайной величины. Для
дискретной и непрерывной случайной величины
D(X) =
2
σ =
()
2
1
() ()
n
ii
i
x
MX px
=
−
∑
,
29
D(X) =
()
2
()xMX
∞
−∞
−
∫
f(x)dx,
D(X) = M
(
)
()
22 2
[()] []XMX MX MX−=− .
Среднеквадратическое отклонение
()DX =
2
σ
= σ.
Размерность
()DX совпадает с размерностью Х. Если
распределение случайной величины неизвестно, но имеется выборка
значений случайной величины объемом n, то оценку математического
ожидания и дисперсии можно произвести по следующим формулам:
1
1
n
i
i
Xx
n
=
=
∑
;
2
2
1
1
()
1
n
i
i
SxX
n
=
=−
−
∑
.
Введем понятие центрированной и нормированной случайной
величины. Отклонение случайной величины Х от ее математического
ожидания М(Х), т.е. X
&
= Х – М(Х), называют центрированной
случайной величиной. М( X
&
) = 0, а σ
2
( X
&
) = σ
2
(Х). Нормированной
случайной величиной называют центрированную случайную
величину, выраженную в долях среднеквадратического отклонения:
Z =
() ()
()XXMX
XX
−
=
σσ
&
,
M(Z) = 0,
D(Z) = 1.
Некоторые дискретные распределения
Ниже приводятся распределения, которые чаще других
используются при расчетах надежности.
Биномиальное распределение
Имеем два возможных исхода в результате испытания:
появление интересующего нас события или его отсутствие.

30
Испытания независимы. р – вероятность появления события, р = const
от серии к серии, q – вероятность появления противоположного
события (отсутствия интересующего нас события). Предположим, что
из n исходов к – благоприятные, тогда
()
1
nk
k
pp
−
− есть вероятность
пересечения к удачных исходов и (n – k) неудачных. Число способов,
которыми можно получить k удачных исходов из n
()
!
!!
k
n
n
C
knk
=
−
,
следовательно
() ( )
1
nk
kk
nn
pk Cp p
−
=− – формула Бернулли.
М = np,
σ
2
= np(1 – p).
Пример 2.3. Электроэнергетическая система имеет 150
генераторных блоков. Вероятность отказа блока 0,06. Определить
вероятность того, что в данный момент не работают два блока
р =
22148
150
0,06 0,94 0,00424C ==
.
Распределение Пуассона (закон редких событий)
Если n велико, а р мало, прибегают к помощи асимптотической
формулы Пуассона. Допущение – np = const = a (среднее число
появлений события в различных сериях испытаний остается
неизменным). Из формулы Бернулли
( 1)( 2)...[ ( 1)]
() (1 )
!
knk
n
nn n n k
Pk p p
k
−
−
−−−
=−
,
так как pn = a , то p = a/n.
Итак, переходя к пределу,
()
12 1
() (1 1 1 ...1 1
lim lim
!
nk
k
n
nn
aka
Pk
knnnn
−
→∞ →∞
−
⎛⎞⎛⎞⎛ ⎞⎛⎞
=⋅−−−−
⎜⎟⎜⎟⎜ ⎟⎜⎟
⎝⎠⎝⎠⎝ ⎠⎝⎠
(1 ) . 1 1
lim lim
!!
k
kk
n
a
nn
aaa
an
knk
−
−
→∞ →∞
⎛⎞
=− −=⋅
⎜⎟
⎝⎠
l
,
следовательно,
