Гук Ю.Б. Теория надежности. Введение: учеб. пособие
Подождите немного. Документ загружается.


31
()
!
ka
n
a
Pk
k
−
=
l
.
Эта формула выражает закон распределения Пуассона.
Математическое ожидание и дисперсия при этом равны
параметру a (M = D = a).
Пример 2.4. Партия реле 200 шт. Вероятность что реле окажется
дефектным р = 0,01. Имея в виду, что a = 200·0,01 = 2, вероятность
того, что в партии не будет дефектных реле, составит:
0
200
2 exp( 2)
(0) 0,135
0!
P
⋅−
==
.
Вероятность того, что в партии будет одно дефектное реле:
1
200
2exp(2)
(1) 0,271
1!
P
⋅−
==
.
Некоторые непрерывные распределения
Рассматриваемые ниже распределения определяются своими
плотностями f(x) и функциями F(x).
Экспоненциальное распределение (рис. 2.7, рис. 2.8)
f(x) =
exp( ) при 0,
0 при 0,
xx
x
λ−λ ≥
⎧
⎨
<
⎩
λ – постоянная положительная величина;
F(x) =
1 exp( ) при 0,
0 при 0.
xx
x
−−λ ≥
⎧
⎨
<
⎩
Это распределение определяется одним параметром λ.
M =
1
λ
,
σ
2
=
2
1
λ
.
F(x) =
0
0
() 0 1
xx
x
x
f x dx dx dx
−
λ−λ
−∞ −∞
=⋅+λ =−
∫∫∫
ll.
Числовые характеристики показательного распределения

32
00
() ()
x
M
Xx
f
xdx x dx
∞∞
−λ
==λ
∫∫
l .
Интегрируя по частям, получим:
М(Х) =
1
λ
.
222
2
00
1
() () [ ()]
x
DX x f xdx M X x dx
∞∞
−λ
=−=λ−
∫∫
λ
l =
22 2
21 1
−=
λλλ
.
Следовательно,
D(X) =
2
1
λ
,
1
()Xσ=
λ
.
Рис. 2.7. Плотность
экспоненциального
распределения
Рис. 2.8. Функция
экспоненциального
распределения
Вероятность попадания в заданный интервал (а, b):
P(a < X < b) = F(b) – F(a) =
ax bx
−
−
−
ll,
так как
F(a) = 1 –
ax
−
l ; F(b) = 1 –
bx
−
l .
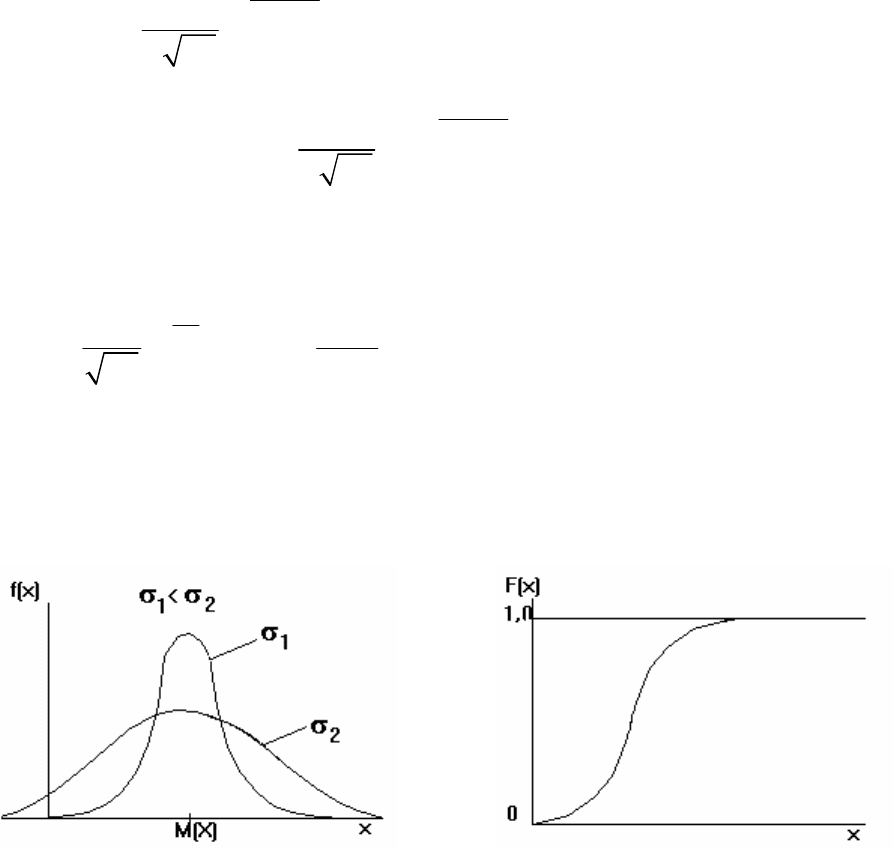
Нормальное распределение (рис. 2.9, рис. 2.10)
33
Характеризуется двумя параметрами. Оно является предельным
(к нему приближаются другие распределения). Плотность и функция
распределения вероятностей случайной величины выражаются через
математическое ожидание и дисперсию
f(x) =
2
()
2
2
1
2
xa
dx
−
−
σ
σπ
l
,
F(X) =
2
()
2
2
1
()
2
xa
x
x
f
xdx dx
−
−
σ
−∞
−
∞
=
∫
σπ
∫
l .
Среднеквадратическое отклонение нормального распределения
равно параметру σ, а математическое ожидание – а. При а = 0 и σ = 1
2
2
1
()
2
z
fz
−
=
π
l , где
x
a
z
−
=
σ
, называют нормированной плотностью.
Нормированную плотность распределения используют для расчета
теоретической кривой распределения, соответствующей данному
ряду статистики. Функция f(z) – четная, т.е. f(z) = f(–z).
Рис. 2.9. Плотность нормального
распределения
Рис. 2.10. Функция
нормального распределения

34
Функция f(z) табулирована. Функция распределения
нормированной случайной величины
F
0
(z) =
2
2
1
2
z
z
dz
−
−∞
π
∫
l .
При практических расчетах используют функцию Лапласа
Ф(z) =
2
2
0
1
2
z
z
dz
−
π
∫
l .
Значения этой функции приводятся в справочниках по
статистике. Ф(z) – нечетная функция, т.е. Ф(–z) = –Ф(z). Функции
F
0
(z) и Ф(z) связаны следующим соотношением:
F
0
(z) =
222
0
222
0
111
222
zzz
zz
dz dz dz
−−−
−
∞−∞
=+
πππ
∫∫∫
lll = 0,5 + Ф(z),
так как первое слагаемое численно равно половине площади под
кривой нормированной плотности распределения, а второе функции
Лапласа.
Вероятность попадания случайной величины в интервал (a, b)
равна разности значений функции распределения на концах этого
интервала
P(a<X<b) = F(b)–F(a) = 0,5 + Ф(z
2
) – (0,5 + Ф(z
1
)) = Ф(z
2
) – Ф(z
1
),
где
z
1
=
()
()
aMX
X
−
σ
,
z
2
=
()
()
bMX
X
−
σ
.
Функции двух случайных аргументов
Если в каждой паре возможных значений случайных величин
X
и
Y соответствует одно возможное значение случайных величин Z, то
Z называют функцией двух случайных аргументов X и Y:
35
Z = φ(X, Y)
Рассмотрим функцию
Z = X+Y.
1. Пусть
X и Y – дискретная независимая случайная величина.
Чтобы найти закон распределения функции
Z = X + Y, необходимо
найти все возможные значения
Z и их вероятности. Например:
Х = [1; 2]; p = [0,4; 0,6].
Y = [3; 4]; p = [0,2; 0,8].
Возможные значения
Z есть суммы каждого возможного
значения
Х со всеми возможными значениями Y:
Z = [1+3, 1+4, 2+3, 2+4] = [4, 5, 5, 6].
Найдем вероятности:
Z = 4 тогда, когда X = 1 и Y = 3.
Вероятности этих значений 0,4 и 0,2. Так как
X и Y независимы, то
вероятность
Z = 1 + 3 = 4 по теореме умножения p = 0,4·0,2 = 0,008.
Аналогично:
р(Z = 1 + 4 = 5) = 0,4·0,8 = 0,32;
p(Z = 2 + 3 = 5) = 0,6·0,2 = 0,12;
p(Z = 2 + 4 = 6) = 0,6·0,8 = 0,48.
Следовательно,
Z = [4; 5; 6]; p = [0,08; 0,44; 0,48].
Проверяем: 0,08 + 0,44 + 0,48 = 1.
2. Пусть
X и Y непрерывные независимые случайные величины.
Доказано: дифференциальная функция
g(z) суммы Z = X + Y может
быть найдена по равенству
g(z) =
12
() ( )
f
xf z xdx
∞
−∞
−
∫
или
g(z) =
12
()()
f
zyfydy
∞
−∞
−
∫
,
где
f
1
и f
2
– дифференциальные функции аргумента.
Если возможные значения аргументов неотрицательны, то

36
g(z) =
12
0
() ( )
z
f
xf z xdx−
∫
или
g(z) =
12
0
()()
z
f
zyfydy−
∫
.
Дифференциальную функцию суммы независимых случайных
величин называют композицией или сверткой. Закон распределения
вероятностей называется устойчивым, если композиция таких
закономерностей есть тот же закон.
3. ПОКАЗАТЕЛИ НАДЕЖНОСТИ
3.1. Невосстанавливаемые объекты
Показатель надежности – количественная характеристика
одного или нескольких свойств, составляющих надежность объекта.
Единичный показатель характеризует одно из свойств надежности, а
комплексный – несколько.
Одной из основных характеристик надежности объекта является
время его безотказной работы или наработка до отказа. Обозначим
эту случайную величину Т. Будем считать, что в момент времени t = 0
объект начинает работу, а в момент
t = T происходит отказ. Закон
распределения случайной величины
Т
F(t) = Р(T < t) = Q(t).
Функция
Q(t) есть вероятность отказа элемента до момента t.
Плотность распределения вероятности отказа
0
()
()
lim
t
Pt T t t
ft
t
∆→
<≤+∆
=
∆
=
()
()
dF t
F
t
dt
′
= ,
где
f(t) – плотность вероятности отказа для момента времени t.
Статистически
f(t) определяется как

37
00
( ) () () ( )
()
mt t mt Nt N t t
ft
Nt Nt
+∆ − − +∆
==
∆∆
)
,
где
m(t) – количество объектов, отказавших к моменту t; N
0
–
количество испытываемых объектов (исправных в начальный момент
времени
t = 0);
N(t) – количество объектов исправных в момент времени t.
Безотказная работа – противоположное событие по отношению
к событию отказа, поэтому вероятность безотказной работы в течение
времени
t:
R(t) = 1 – Q(t) = Р(T > t)
Рис. 3.1. Вероятность отказа и вероятность безотказной работы
Функцию
R(t) (рис. 3.1) называют функцией надежности [11].
Статистически она определяется как:
0
()
()
Nt
Rt
N
=
)
.
Надежность элемента
R = Р(T > t
m
),
где
t
m
– срок службы (период, в течение которого элемент
должен выполнять заданные функции). Вероятность отказа и
вероятность безотказной работы объекта в течение времени
t
р
определяется через плотность вероятности отказа.

38
Поскольку вероятность отказа элемента равна:
0
() ()
t
p
p
Qt f tdt=
∫
, то
00
()1 () () () ()
p
p
t
pp
t
R t Q t f t dt f t dt f t dt
∞∞
=− = − =
∫∫∫
, так как:
0
() 1
f
tdt
∞
=
∫
.
Рис. 3.2. Характеристики
надежности невосстанавливаемого
объекта
Рис. 3.3. К определению
средней наработки до отказа
Среднее время безотказной работы определяется как
математическое ожидание случайной величины
00
000
( ) () () () ()T MT tf tdt tRt Rtdt Rtdt
∞∞∞
∞
== =− + =
∫∫∫
.
Графически эти зависимости представлены на рис. 3.2 и 3.3.
Статистически
0
0
1
0
1
ˆ
N
i
i
Tt
N
=
=
∑
,
где
t
i
– наработка до отказа i-го объекта. При этом испытания
проводятся до тех пор, пока все объекты не откажут. В противном
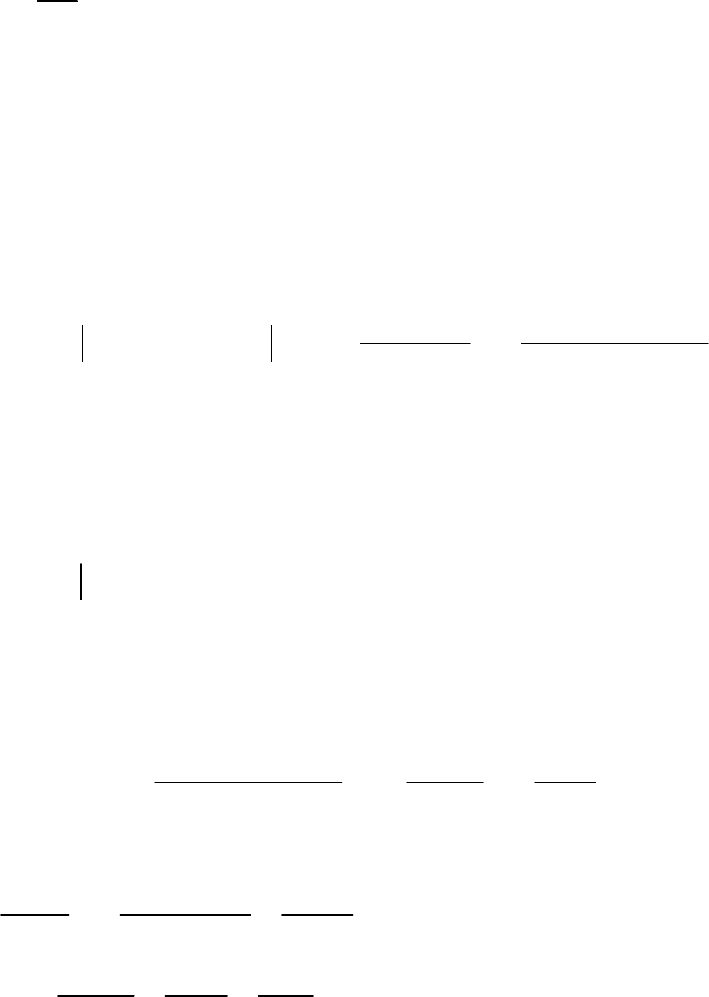
39
случае, если испытания заканчиваются только при отказе m объектов
(из-за недостатка времени), то:
00
1
0
1
()
m
i и
i
TttNm
N
=
⎡⎤
≈+−
⎢⎥
⎣⎦
∑
)
,
где
t
и
– время испытания.
В практических расчетах самой распространенной
характеристикой надежности является интенсивность отказов λ(
t).
Она определяется как плотность условной вероятности отказа в
момент
t, при условии, что до этого момента объект работал
безотказно. Условная вероятность отказа на интервале (
t, t + ∆t):
() ()()
()1()1
() ()
Rt t Rt t Rt
Qt tt Rt tt
Rt Rt
+
∆+∆−
+∆ = − +∆ = − =−
,
где
R(t + ∆t) – вероятность совместного события безотказной
работы на интервале времени (0,
t) и (t, t + ∆t);
R(t) – вероятность безотказной работы на интервале времени
(0,
t);
()Rt tt+∆
– условная вероятность безотказной работы на
интервале (
t, t + ∆t), при условии, что на интервале (0, t) наблюдалась
безотказная работа. Используя последнее уравнение, по определению
λ(
t) получим:
( ) () () ()
() lim
() () ()
t
Rt t Rt dRt R t
t
tR t dtR t R t
∆→∞
′
⎡⎤
+∆ −
λ= − =− =−
⎢⎥
∆
⎣⎦
.
Так как
() (1 ()) ()dR t d Q t dQ t
dt dt dt
−
−=− =
, то
() () ()
()
() () ()
dQ t Q t f t
t
dtRt Rt Rt
′
λ= = =
.
В случае малых интервалов ∆
t:
Q(t, t + ∆t)
≅
λ(t)∆t.
40
Величина λ(t) является локальной характеристикой надежности,
определяющей надежность объекта в каждый данный момент
времени. Иначе λ(
t) есть вероятность того, что объект, проработавший
безотказно до момента
t, откажет в последующую единицу времени
(если эта единица мала).
Из уравнения
()
()
()
Rt
t
Rt
′
λ=− определим вероятность безотказной
работы в течение времени
t:
00
1
() () ln ()
()
tt
tdt dRt Rt
Rt
λ=− =−
∫∫
,
0
()
()
t
tdt
Rt
−λ
∫
= l
.
Вероятность безотказной работы на интервале (
t
1
, t
2
) будет
2
1
()
12
(, )
t
t
tdt
Rt t
−λ
∫
= l
.
Статистически
00
0
0
0
() ( )
() () ( )
()
()
() ()
()
()
()
()
Nt Nt t
NN
Rt Rt Rt t
t
Nt
Rt tRt
t
N
mt
N
mt
Nt
tN t
t
N
+
∆
−
′
−+∆
λ=− ≅ ≅ =
∆
∆
∆
∆
==
∆
∆
)
где m(∆t) – количество отказов на интервале (t, t + ∆t);
N(t) – количество неотказавших объектов на момент t. Эта
формула справедлива при малых ∆t и больших m(∆t); λ(t) имеет
размерность обратную времени (1/час, 1/год).
