Гук Ю.Б. Теория надежности. Введение: учеб. пособие
Подождите немного. Документ загружается.


41
Опыт эксплуатации и испытаний показывает, что функция λ(t)
имеет характерный "корытообразный" вид (рис. 3.4).
У кривой можно выделить три участка. Эти участки
соответствуют следующим периодам "жизни" объекта: приработки,
нормальной работы и старения. В период нормальной работы
преобладают случайные отказы, в период старения – износовые
отказы.
Рис. 3.4. Изменение интенсивности отказов в течение эксплуатации
Для периода нормальной работы можно принять λ(t) = const, и
тогда формулы вычисления надежности:
()
t
Rt
−λ
= l ,
()
t
Rt tt
−λ∆
+∆ =l ,
() 1
t
Qt
−λ
=−l ,
()
t
ft
−λ
=λl ,
0
0
0
11
t
t
Tdt
∞
∞
−λ
−λ
==−=
λλ
∫
l
l
.
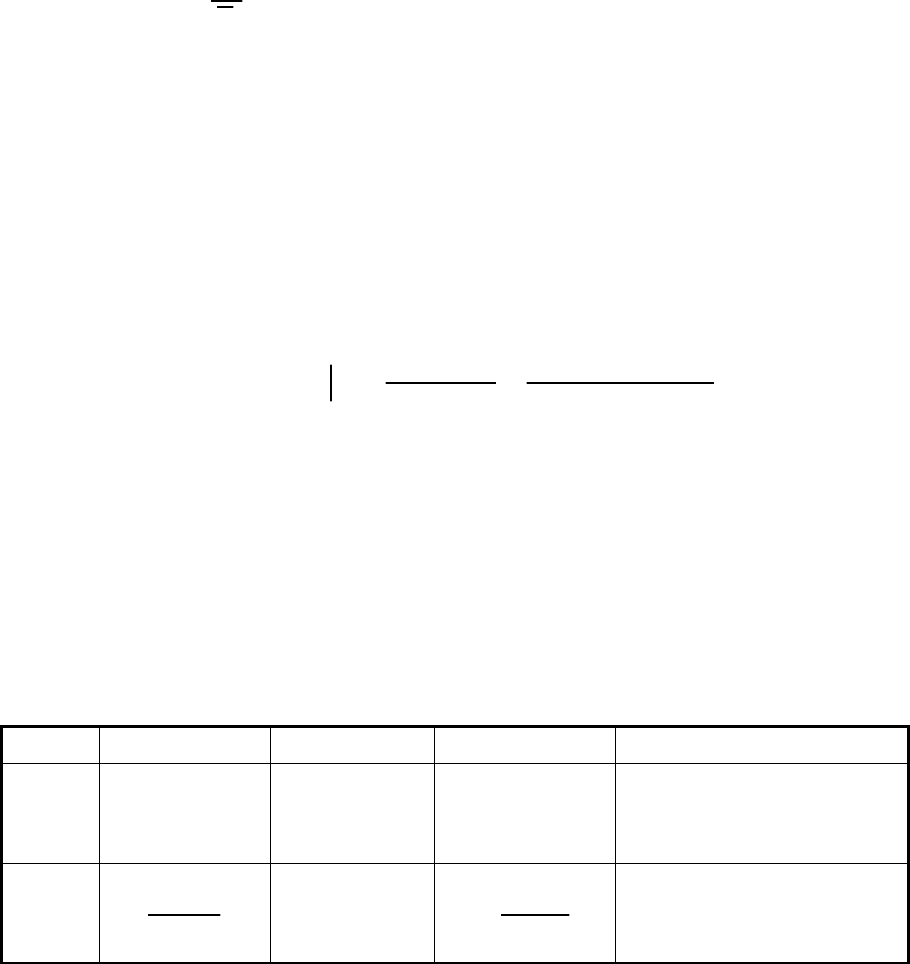
Следовательно, при экспоненциальном распределении
наработки до отказа:
( ) exp( )
()
( ) exp( )
ft t
t
Rt t
λ−λ
λ= = =λ
−λ
,
42
т. е. интенсивность отказов равна параметру λ
экспоненциального закона распределения.
В тех случаях, когда t << T
0
, можно использовать более простые
выражения:
() 1
R
tt=−λ,
0
()
t
Qt t
T
=λ = .
Экспоненциальный закон распределения наработки до отказа
используется очень широко. Почти все формулы для расчета
надежности резко упрощаются, а вероятность безотказной работы на
заданном интервале времени (t, t + ∆t) не зависит от времени
предшествующей работы t, а зависит только от продолжительности
интервала ∆t. Действительно, вероятность безотказной работы на
(t, t
+ ∆t) равна:
( ) exp( ( ))
( , ) ( ) exp( )
( ) exp( )
Rt t t t
R
tt t Rt tt t
Rt t
+
∆−λ+∆
+∆ = +∆ = = = −λ∆
−λ
.
Кроме экспоненциального закона используются и другие. Так
процесс старения хорошо описывается нормальным законом
распределения. Каждую из функций
Q(t), R(t), f(t) и λ(t) можно
выразить через любую другую. Связи между ними приведены в
табл. 3.1.
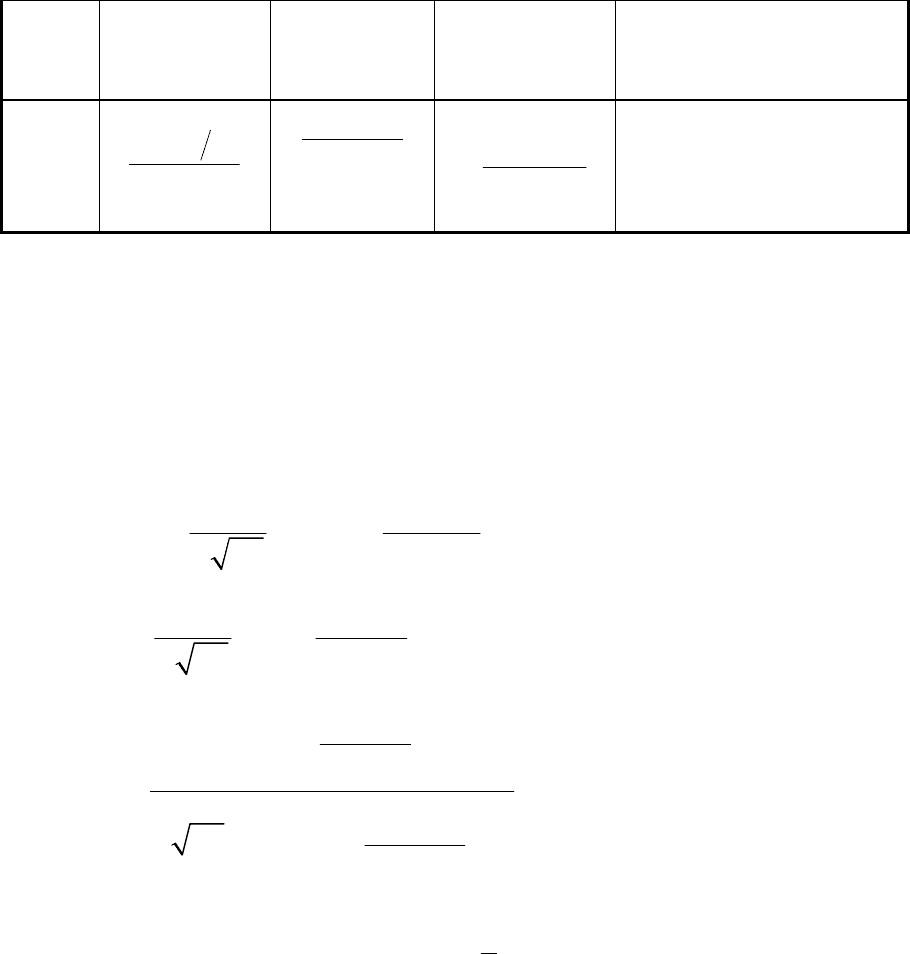
Таблица 3.1
Связь между функциями Q(t), R(t), f(t) и λ(t)
Q(t) f(t) R(t) λ(t)
Q(t) –
0
()
t
f
tdt
∫
1()
R
t
−
0
1exp ()
t
tdt
⎡⎤
−−λ
⎢⎥
⎣⎦
∫
f(t)
()dQ t
dt
–
()dR t
dt
−
0
()exp ()
t
ttdt
⎡⎤
λ−λ
⎢⎥
⎣⎦
∫
43
R(t)
1()Qt−
()
t
f
tdt
∞
∫
–
0
exp ( )
t
tdt
⎡⎤
−λ
⎢⎥
⎣⎦
∫
λ(t)
()
1()
dQ t dt
Qt−
()
()
t
f
t
f
tdt
∞
∫
ln ( )dRt
dt
−
–
Кроме экспоненциального закона в теории надежности
используются и другие. Так, для стареющих объектов применяются
нормальное распределение и распределение Вейбулла. Последнее
может также описывать и явление приработки.
Для нормального распределения
2
2
1()
() 1 exp
2
2
t
xa
Rt dx
−∞
⎡
⎤
−
=− −
⎢
⎥
σπ
σ
⎢
⎥
⎣
⎦
∫
;
2
2
1()
() exp
2
2
ta
ft
⎡⎤
−
=−
⎢⎥
σπ
σ
⎢⎥
⎣⎦
;
2
2
2
()
exp
2
()
2
()
2exp
2
t
ta
t
xa
dx
−∞
⎡⎤
−
−
⎢⎥
σ
⎣⎦
λ=
⎡⎤
−
⎢⎥
σπ− −
σ
⎢⎥
⎣⎦
∫
,
где
a – математическое ожидание; σ – среднее квадратическое
отклонение наработки до отказа;
a =
0
T .
Для распределения Вейбулла
() exp( )
k
Rt t=−α;
1
( ) exp( )
kk
f
tkt t
−
=α −α ;
1
()
k
tkt
−
λ=α ;

44
0
1/
1
1
k
Г
k
T
⎛⎞
⎜⎟
+
⎝⎠
=
α
,
где α,
k – параметры распределения Вейбулла;
Г – гамма-функция:
1
0
()
nt
Г
nt dt
∞
−−
=
∫
l ,
при целых
n
Г(n) = (n – 1)!
Если
k = 1, распределение Вейбулла совпадает с
экспоненциальным. С другими распределениями можно ознакомиться
в справочниках.
3.2. Объекты с мгновенным восстановлением
Эксплуатация восстанавливаемого объекта не прекращается при
его отказе. Объект ремонтируется или заменяется новым. Наработка
между отказами и продолжительность восстановления являются
случайными величинами. Практически время восстановления
значительно меньше, чем наработка между отказами. Поэтому имеет
смысл рассмотреть случай с мгновенным восстановлением, когда
время восстановления пренебрежимо мало по сравнению с
наработкой между отказами.
Объект
начинает работать в момент t = 0. Через случайное время
T
1
в момент t
1
наступает первый отказ. В этот же момент объект
восстанавливается и продолжает нормально функционировать. В
момент
t
2
по истечении времени Т
2
происходит второй отказ с
последующим восстановлением (рис. 3.5.) .
Последовательность отказов, происходящих в случайные
моменты времени
t
i
, называется потоком отказов. В случае
независимости наработок между отказами, имеющих одинаковые
законы распределения
F
T
(t) = P(T
k
< t), Этот процесс называют

45
процессом восстановления. Средняя наработка между отказами
(наработка на отказ) определяется как математическое ожидание:
()
0
0
() 1 ()
kT
TMT Ftdt
∞
==−
∫
.
Рис. 3.5. Поток отказов
(восстановлений) объекта с
мгновенным восстановлением
Рис. 3.6. Соотношение между
случайными моментами
времени отказов и
количествами отказов
Плотность распределения вероятностей времени до первого
отказа
f
1
(t), до второго – f
2
(t), до k-го – f
k
(t). Предположим, что первый
отказ произошел в некоторый момент времени τ (τ – случайная
величина), а второй – в момент времени
t. Тогда наработка на второй
отказ равна (
t – τ). Вероятность того, что второй отказ произойдет в
интервале (
t, t + ∆t) для каждого значения τ равна [5]
211
() ( ) ( )
f
tt f ft t∆ ≈ τ∆τ −τ∆
и для всех τ <
t
211
0
() ( ) ( )
t
f
t
ff
td=τ−ττ
∫
.
Для
k-го отказа
11
0
() ( ) ( )
t
kk
f
t
ff
td
−
=τ−ττ
∫
,
так как
f
T
(t) = f
1
(t), то все f
k
(t) выражаются через f
T
(t).
46
Поток отказов можно описать продолжительностью времени до
k-го отказа t
k
= T
1
+ T
2
+ … + T
k
или последовательностью случайных
чисел отказов
h(t), которые могут возникнуть за время t (рис. 3.6). Из
очевидного соотношения между
h(t) и t
k
следует, что
Р(t
k
< t) = P[h(t) ≥ k].
Значения
h(t) определяются из условия
() ()ht ht
ttt
<
≤
.
Закон распределения
h(t)
[]
(
)
12
() () ( ... ) ()
kk kk
F
tPhtkPttPTT TtQt=≥=<=+++<=,
где
Q
k
(t) – вероятность того, что за время t возникнет количество
отказов, большее или равное заданному числу
k. Функция Q
k
(t)
определяется как
k-кратная свертка функции Q
1
(t).
1
0
() ( ) ( )
t
kk T
Qt Q t dQ
−
=−ττ
∫
,
так как
Q
1
(t) = F
T
(t) = Q
T
(t).
Вероятность того, что за время
t произойдет ровно k отказов,
определяется следующим образом:
P[h(t) = k] =
1
() () ()
kkk
Pt Q t Q t
+
=− .
Математическое ожидание числа отказов, происшедших до
момента времени
t, называется функцией отказов (восстановлений)
или ведущей функцией
H(t) [4]:
[]
1
11
12 1
() [ ()] () () ()
() ( 1) () (),
kkk
kk
kkk
kk k
H
tMht kPt kQtQt
kQ t k Q t Q t
∞∞
+
==
∞∞ ∞
== =
== = −=
=−−=
∑∑
∑∑ ∑
иначе [4],
0
() () ( ) ( )
t
H
tQt Ht dQ=+ −ττ
∫
.
Среднее число отказов на интервале (
t
1
, t
2
) равно H(t
2
) – H(t
1
).

47
Интенсивность потока отказов в момент времени t равна
среднему числу отказов, происшедших в единицу времени, начиная с
момента
t, при условии, что эта единица времени достаточно мала,
11
()
()
() ()
k
k
kk
dP t
dH t
tftk
dt dt
∞∞
==
Λ= = =
∑∑
.
Приближенно она равна безусловной вероятности отказа за
единицу времени.
Параметр потока отказов определяется как плотность
вероятности отказа восстанавливаемого объекта – предел отношения
вероятности отказа в интервале времени
∆
t непосредственно после
момента
t к продолжительности этого интервала при его
неограниченном уменьшении
00
(, ) 1 (, )
() lim lim
tt
Qttt Rttt
t
tt
∆→ ∆→
+∆ − +∆
ω= =
∆∆
,
где R(t, t +
∆
t) – вероятность безотказной работы на интервале
времени ∆
t. Выразим ω(t) через f
k
(t). Полная вероятность отказа в
интервале (
t, t + ∆t) равна сумме вероятностей того, что в этом
интервале произойдет первый отказ, второй отказ и т. д.:
Q(t, t +∆t) =
1
()
k
k
Qt
∞
=
∑
.
Поэтому
1
() ()
k
k
tft
∞
=
ω=
∑
;
() ()
tt
p
p
t
H
td
+
=ωττ
∫
.
Ниже (рис. 3.7) приводится диаграмма параметра потока отказов
при нормальном законе распределения времени наработки между
отказами.
С увеличением k кривая f
k
(t) становится все более широкой и
пологой, так как накапливаются неопределенности значений
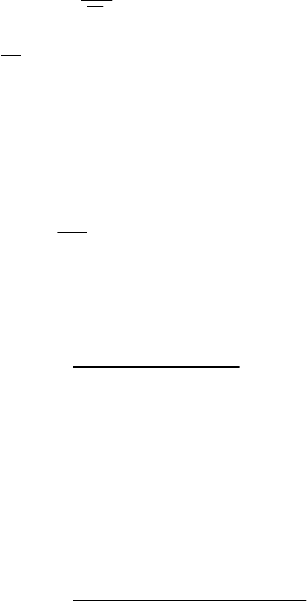
48
предыдущих наработок. В общем случае вычислить функцию ω(t)
трудно. При практических расчетах на поток восстановлений
накладывают ряд ограничений.
С течением времени процесс возникновения отказов становится
стационарным и его локальные характеристики перестают зависеть от
времени:
0
1
lim ( )
t
t
T
→∞
ω= ,
где
T
0
– наработка на отказ.
В практических расчетах часто используется средний параметр
потока отказов (частота отказов)
1
() ()
p
tt
p
p
t
td
t
+
ϖ= ωττ
∫
.
На расчетном интервале времени (t
1
, t
2
):
21
12
21
() ()
(, )
H
tHt
tt
tt
−
ω=
−
.
Статистически среднее количество отказов в единицу времени
(год) отнесенное к одному элементу определяется как:
00
21
11
12
02 1
() ()
(, )
()
NN
ii
ii
mt mt
tt
Nt t
==
−
ω=
−
∑∑
,
где m
i
(t
1
) и m
i
(t
2
) – числа отказов i-го объекта до моментов
времени t
1
и t
2
;
N
0
– число испытываемых объектов.
В случае экспоненциального закона распределения наработок на
отказ процесс отказов и восстановлений будет образовывать поток
событий, называемый пуассоновским.
Потоки отказов (событий) обладают рядом свойств.

49
1. Свойство ординарности. Вероятность совмещения двух или
более событий в один и тот же момент времени очень мала (равна
нулю),
1
0
(, )
() () lim
t
Ptt t
tt
t
∆→
+
∆
ω=λ≈
∆
,
где P
1
– вероятность одного события.
2. Свойство стационарности. Вероятность появления k событий
на любом промежутке времени зависит только от числа k и от
длительности ∆t и не зависит от начала отсчета:
ω(t) = ω = const; λ(t) = λ = const,
а если поток и ординарный, то ω = λ = const.
3. Свойство отсутствия последействия (без последействия).
Число событий для
любых неперекрывающихся интервалов времени
независимы.
Рис. 3.7. Параметр потока отказов при нормальном законе
распределения наработок между отказами
Ординарные потоки без последействия называются
пуассоновскими. Поток, обладающий свойствами стационарности,
ординарности и отсутствия последействия, считается простейшим
потоком или однородным пуассоновским.
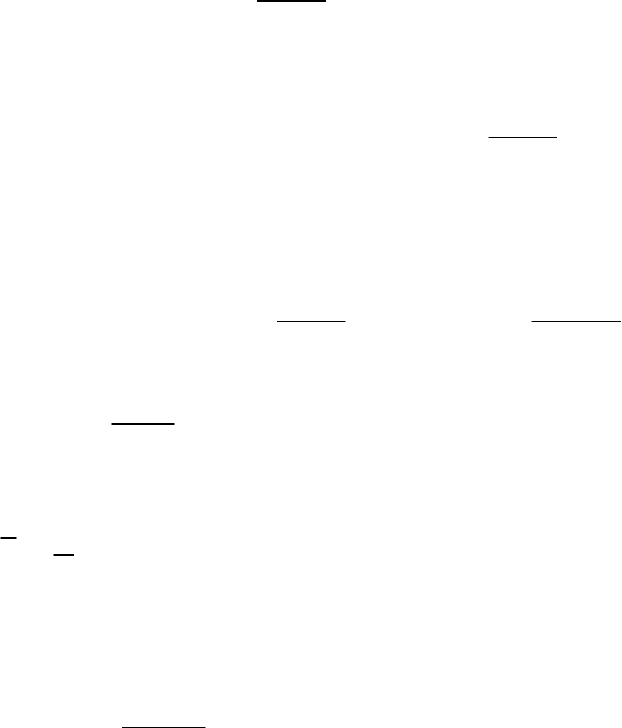
50
Для простейшего потока среднее число событий – att=ω =λ и
все выше рассмотренные показатели вычисляются по следующим
формулам:
-
[]
()
() () exp( )
!
k
k
t
Pt Pht k t
k
λ
=== −λ
(вероятность k событий за
время t);
-
[]
()
0
0
() () () 0 exp( ) exp( )
0!
t
Pt Rt Pbt t t
λ
== == −λ=−λ
(вероятность отсутствия отказов);
-
() 1 exp( )Qt t=− −λ;
-
() ()
1
00 1
() ()
!(1)!
kk
tt
k
kk k
tt
Ht kP t k t
kk
−
∞∞ ∞
−λ −λ
== =
λλ
== =λ =
−
∑∑ ∑
ll
()
0
!
i
ttt
i
t
ttt
i
∞
−λ −λ λ
=
λ
=λ =λ=λ
∑
lll
;
- Λ(
t) = λ
k
(t) = λ = const;
-
0
1
T =
λ
так как среднее число отказов за единицу времени
H(t)/t
есть обратная величина наработки на отказ и численно равна частоте
отказа;
-
1
()
(1)!
k
kt
k
t
ft
k
−
−λ
=λ
−
l
получена из
11
0
() ( ) ( )
t
kk
f
t
ff
td
−
=τ−ττ
∫
после подстановки
1
()
t
ft
−λ
=λl ;
() 2 2 2
2
000
()
ttt
tttt
ft d d d t
−λτ −λ −τ −λτ−λ +λτ −λ −λ
=λ λ τ=λ τ=λ τ=λ
∫∫∫
ll l l l
;
