Гук Ю.Б. Теория надежности. Введение: учеб. пособие

Подождите немного. Документ загружается.

111

записан код аварии k. Через косую черту записываются коды к

о.п

/ к

в.р

Для каждого из режимов j записывается код развития аварии при

отказе РЗ – к

о.с

, если код отличается от к

о.п

или к

в.р

этого же режима.

Значения τ(к

о.п

) и τ(к

о.с

) определяются экспертным путем.

Среднее аварийное снижение годовой выработки энергии

станцией (или отпуска энергии при аварии на подстанции)

рассчитывается по формуле

()

()()

(

)

(

)

()

{

}

()()()

ст о.пв.ро.по.пв.рв.ро.п

о.со.со.с

8760 /

8760 ,

WKKNKKNKKK

KKNK

λτττ

λτ

⎡

⎤

∆= ∆ +∆ − +

⎣

⎦

+∆

∑

где ∆N(к

в.р

), ∆N(к

о.п

), ∆N(к

о.с

) – аварийное снижение мощности,

определяется мощностью отключаемых при k-й аварии агрегатов за

вычетом возможного увеличения мощности оставшихся в работе, т.е.

с учетом резерва.

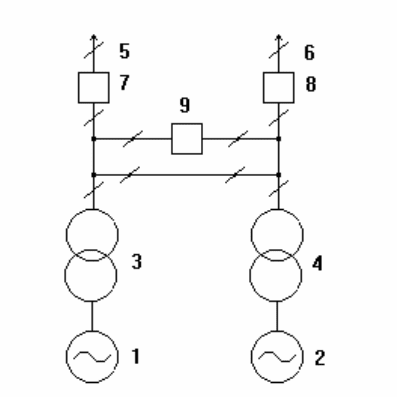
В качестве примера рассмотрим схему выдачи мощности от

гидроэлектростанции (рис. 5.9).

Рис. 5.9. Схема выдачи мощности от гидроэлектростанции

112

Исходные данные для расчета надежности схемы даны в табл.

5.2.

Таблица 5.2

Показатели надежности элементов схемы (к рис.5.9)

Элемент № λ, год

–1

τ, год q

пл

Гидрогенератор 25 МВт 1, 2 0,1 0,02 0,02

Трансформатор 110 кВ 3, 4 0,01 0,01 0,002

ВЛ 110 кВ 5, 6 1,0 0,001 0,01

В 110кВ 7 – 9 0,02 0,002 0,004

Расчетные режимы

j = 1 – ремонт блока генератора 1 и трансформатора 3;

j = 2 – ремонт блока генератора 2 и трансформатора 4;

j = 3 – ремонт высоковольтной линии ВЛ5 и выключателя В7;

j = 4 – ремонт высоковольтной линии ВЛ6 и выключателя В8;

j = 5 – ремонт выключателя В9.

Относительная длительность расчетных режимов

11133пл1

0,0221qq=λτ +λ τ + = ;

22244пл2

0,0221qq=λ τ +λ τ + = ;

34 5577пл5

0,01104qq q==λτ+λτ+ = ;

599пл9 пл9

0,00004 0,004 0,00404;

1 1 0,05928 0,94072.

=λ τ +λ τ = + =

=− =− =

∑

Расчетными авариями и их кодами являются следующие:

•

потеря одного генератора – 1Г;

•

потеря одной высоковольтной линии – 1Л;

•

потеря одного генератора и одной высоковольтной линии –

1Г1Л;

• полное погашение схемы – 2Г2Л, и так далее.

В первых двух колонках каждого режима j таблицы расчетных

связей приводятся коды кратковременных и за значком '/' –

113

длительных аварий, а в соседних колонках – коды аварий при отказе

РЗ. Если при отказе i-го элемента кратковременная и длительная

аварии одинаковы, то на месте кода кратковременной аварии ставится

прочерк, чтобы не учитывать аварию дважды.

Пользуясь табл. 5.3 расчетных связей, запишем формулы для

вычисления частот расчетных аварий:

12340

(1Г1Л)( )qλ =λ+λ+λ+λ ,

()

(

)( )

56012 7182

/1Л qqq q qλ − = λ +λ + + +λ +λ ,

780

(1Г1Л/1Л)( )qλ=λ+λ,

(2Г2Л /) qλ−=λ,

241 132

(1Г2Л/1Г)( ) ( )qqλ=λ+λ+λ+λ,

()

81 7 2

1Г2Л/1Л qqλ=λ+λ,

()()

91 2

1Г2Л/ qqλ−=λ+

133 2 44

(/1Г)( ) ( )qqλ− =λ+λ +λ +λ ,

()

(

)

2493 1394

2Г1Л/1Г qqλ=λ+λ+λ+λ+λ+λ,

683 574

(/2Г1Л)( ) ( )qqλ − = λ +λ + λ +λ ,

12345

(2Г2Л/1Г)( )qλ=λ+λ+λ+λ.

56785

(2Г2Л/1Л)( )qλ=λ+λ+λ+λ.

Среднее время восстановления нормального режима выдачи

мощности при длительных авариях рассчитываем по формулам

11 22 33 44 0

(1Г1Л/1Г)( )

(1Г1Л/1Г)

qτ = λ τ +λ τ +λ τ +λ τ

()

()()

55 66 0 1 2 771 882

/1Л

qqq q qτ− = λτ +λτ + + +λτ +λτ

λ−

77 88 0

(1Г1Л/1Л)()

(1Г1Л/1Л)

qτ= λτ+λτ

22 44 1 11 33 2

(1Г2Л/1Г)()()

(1Г2Л/1Г)

qqτ= λτ+λτ+λτ+λτ

114

()

881 77 2

1Г2Л/1Л

qqτ= λτ+λτ

()

99 1 2

1Г2Л /

qqτ−= λτ+

λ−

11 3 3 3 2 2 4 4 4

(/1Г)()( )

(/1Г)

qqτ− = λτ +λτ + λτ +λτ

λ−

()

22 44 99 3

11 3 3 9 9 4

2Г1Л/1Г

τ= λτ+λτ+λτ+

+λτ+λτ+λτ

66 88 3 55 77 4

(/2Г1Л)()()

(/2Г1Л)

qqτ− = λτ +λτ + λτ +λτ

λ−

11 22 33 44 5

(2Г2Л/1Г)( )

(2Г2Л/1Г)

qτ = λ τ +λ τ +λ τ +λ τ

55 66 77 88 5

(2Г2Л/1Л)( )

(2Г2Л/1Л)

qτ= λτ+λτ+λτ+λτ

Таблица 5.3

Таблица расчетных связей

Код аварии в режиме j

i 0 1 2 3 4 5

1Г1Л

/1Г

2Г

2Л

– –

1Г2Л/

1Г

– –/1Г

2Г1

2Г1Л/

1Г

–

2Г2Л/

1Г

–

1Г1Л

/1Г

2Г

2Л

1Г2Л

/1Г

– – –

2Г1Л/

1Г

– –/1Г

2Г1

2Г2Л/

1Г

–

1Г1Л

/1Г

2Г

2Л

– –

1Г2Л/

1Г

– –/1Г

2Г1

2Г1Л/

1Г

–

2Г2Л/

1Г

–

1Г1Л

/1Г

2Г

2Л

1Г2Л

/1Г

– – –

2Г1Л/

1Г

– –/1Г

2Г1

2Г2Л/

1Г

–

5 –/1Л

1Г

1Л

–/1Л – –/1Л

1Г

2Л

– –

–

/2Г1Л

–

2Г2Л/

1Л

–

6 –/1Л

1Г

1Л

–/1Л

1Г

2Л

–/1Л –

–

/2Г1Л

– – –

2Г2Л/

1Л

–

115

1Г1Л

/1Л

2Г

2Л

–/1Л

1Г

2Л

1Г2Л/

1Л

– – –

–

/2Г1Л

–

2Г2Л/

1Л

–

1Г1Л

/1Л

2Г

2Л

1Г2Л

/1Л

– –/1Л

1Г

2Л

–

/2Г1Л

– – –

2Г2Л/

1Л

–

2Г2Л

/–

–

1Г2Л

/–

–

1Г2Л/

–

2Г1Л/

1Г

–

2Г1Л/

1Г

– – –

При отказе срабатывания защиты поврежденного элемента

резервная защита отключает вместе с поврежденным элементом один

или несколько соседних. Условную вероятность отказа защиты Q(s/i)

оценим в 0,5% [7]. Если отказ РЗ не усугубляет тяжесть аварии, то на

месте кода данной аварии ставится пропуск, чтобы не учитывать

аварию дважды.

. 1234780

(2Г2Л) 0,005( )

qλ = λ+λ+λ+λ+λ+λ ,

.560

(1Г1Л) 0,005( )

qλ=λ+λ,

671 582

(1Г2Л) 0,005[( ) ( ) ]qqλ=λ+λ+λ+λ,

133 2 44

(2Г1Л) 0,005[( ) ( ) ]qqλ=λ+λ+λ+λ.

В рассматриваемом случае отказы РЗ увеличивают частоту

аварий не более чем на 10%.

Среднее аварийное снижение годовой выработки энергии

станцией ∆W

ст

рассчитывается по вышеприведенной формуле,

учитывая аварийное снижение мощности в каждой из аварий.

6. АНАЛИЗ НАДЕЖНОСТИ ЭЛЕКТРИЧЕСКОЙ

СЕТИ ЭНЕРГОСИСТЕМЫ

6.1. Общие положения

Электроэнергетическая система представляет собой сложную

структуру с большим количеством элементов. Точное знание

распределения потока мощности и уровней напряжения нужно при

анализе режимной надежности действующей энергосистемы в ходе

116

оперативного управления. Тогда расчеты распределения потока

осуществляются по полным уравнениям с учетом напряжений в

узлах, значений активной и реактивной мощности в ветвях сети и

условий их генерирования в узлах. Но это уже задача расчета

режимов.

Структурная и режимная надежность являются расчетными

моделями надежности системы, когда управление коммутацией сети

осуществляется в случае

отказов элементов по заданным алгоритмам

и программам. Возможные отказы системы (аварии), выявленные при

анализе расчетных моделей, являются расчетными событиями. На них

ориентирована вся структура и автоматика системы. В реальной

жизни в энергосистеме кроме расчетных аварий происходят аварии

нерасчетные, когда в ходе развития первичных отказов имеют место

отказы и неправильные действия

персонала и средств управления, а

также воздействия стихийных сил и посторонних факторов. Эти

явления относятся к области живучести энергосистем [12].

Рассмотрим структурную надежность.

Структура системы меняется как при случайных возмущениях,

так и при преднамеренных переключениях.

Представим электрическую систему эквивалентной схемой

замещения, содержащей генерирующие, нагрузочные и транзитные

узлы, а также связи между ними

. В качестве критерия (условия)

отказа системы будем считать ограничение или прекращение питания

хотя бы одного из нагрузочных узлов. Это может произойти, когда

имеющаяся генерирующая мощность в системе недостаточна для

электроснабжения всех потребителей (дефицит мощности),

перегружены линии электропередачи или прерваны связи

нагрузочного узла с системой. Поэтому кроме вычисления

показателей надежности системы

в целом необходимо определить

надежность электроснабжения отдельных нагрузочных узлов.

117

Если не рассматривать случаи нарушения устойчивости

параллельной работы генераторов системы и выхода за допустимые

пределы напряжений в узлах, относя эти случаи к задачам

обеспечения устойчивоспособности и режимной управляемости, то и

тогда определение показателей безотказности и готовности

электроэнергетической системы представляется сложной задачей.

Наличие большого числа элементов в структуре и их связность по

электрическому режиму, наличие восстановления и профилактики и

ограничений по пропускной способности элементов сети заставляет

принимать при анализе структурной надежности электрических

систем следующие упрощающие допущения [10]:

- отказы элементов системы являются независимыми

событиями;

- поток отказов событий ординарен;

- периоды безотказной работы элементов значительно больше

длительностей их восстановления;

- время безотказной работы и время

восстановления

распределены по экспоненциальному закону;

- рассматриваются только стационарные состояния элементов и

определяются их вероятности (относительные длительности).

Схема замещения электроэнергетической системы представляет

собой сложную сетевую структуру, поэтому при построении ее

модели надежности используется метод путей и сечений на основе

применения теории графов. При этом одновременно с поиском

минимальных путей и сечений

определяются (с помощью алгоритма

поиска максимального потока) и потоки активной мощности. Этот

метод не позволяет точно определить потокораспределение в сети,

так как учитывает только первый закон Кирхгофа. Однако простота

реализации метода является решающим преимуществом при сложных

схемах и большом числе расчетов, когда надо получить скорее

118

качественную, чем количественную оценку надежности

рассматриваемых вариантов схемных решений.

6.2. Элементы теории графов

Графом (Y, B) называется упорядоченная пара множеств:

конечного непустого множества Y, элементы которого y

называются

узлами графа, и множества В, элементы которого b

(i, j) называются

ветвями этого графа. Последние представляют собой пары элементов

множества Y. В дальнейшем для упрощения записи узлы и ветви

графа будем обозначать их индексами: ,iY

∈

где i = 1, 2, ... , n;

(, ) ,ij B∈ где ,.iYjY∈∈ Ветви графа бывают ориентированными и

неориентированными.

Ориентированная ветвь имеет начало и конец

(направление). В связи с этим графы могут быть ориентированными,

неориентированными и смешанными. Ветвь, соединяющая два узла,

инцидентна им и, наоборот, оба узла инцидентны этой ветви.

Два узла (, )ij Y∈ называются

смежными, если соединены

ветвью (, )ij B∈ . Две ветви смежные, если существует хотя бы один

узел, инцидентный им обеим (общий узел).

Путь (1–n) между двумя узлами y

и y

есть последовательность

ветвей, смежных одна с другой {(1,2),...,(l,i),(i,j),(j,h),...,(k,n)}, в

которой у каждой ветви (i, j) один из инцидентных ей узлов i также

инцидентен предыдущей ветви последовательности (l, i), а другой

узел j инцидентен последующей ветви (j, h). Путь, в котором

начальный узел совпадает

с конечным (1 = n), называется контуром

(замкнутым путем). Ориентация отдельных ветвей может не

совпадать с ориентацией пути в целом. Ветви, направление которых

совпадает с направлением пути, называются

прямыми ветвями, а при

несовпадении направлений пути и ветви ветвь называется

обратной.

Граф

связен, если между любыми двумя узлами его можно

проложить путь.

Несвязный граф состоит из нескольких

119

компонентов связности. Деревом называется связный граф, не

содержащий контуров. Между любыми двумя узлами дерева можно

построить (проложить) только один единственный путь.

Разрезом (сечением), отделяющим узел i от узла j, называется

множество ветвей

(, )RR , где

– дополнение R до Y и IR∈ , a jR

∈

Разрез

(, )RR минимален в том случае, если максимальный поток

насыщает все ветви разреза

(, )RR и оставляет свободными все ветви,

принадлежащие разрезу

(,)RR. Всякий разрез, отделяющий узлы i и j,

блокирует все пути, содержащие только прямые ветви, между этими

узлами.

Существует три способа описания графов: аналитический,

геометрический и матричный. Аналитический граф (Y, B) задается в

виде множества узлов

{ , ,..., ,..., }

Yyy y y

, которое имеет

мощность

Yn= , и множества ветвей (упорядоченных пар элементов

множества Y).

{( , ,...,( , ),...,( , )}

ij lm

Byy yy yy= .

Геометрический граф изображается с помощью точек и линий.

Узлы графа – точки, ветви – линии, соединяющие инцидентные им

узлы. Ориентированные ветви изображаются линиями со стрелками.

Графы могут быть заданы с помощью матриц смежности (узлы-

узлы) и матриц инциденций (узлы-ветви). Матрица смежности может

быть квадратной

[]

d= размером nn

, где n – количество узлов; d

– количество ветвей, соединяющих узлы

i и j. Возможно так же

записывать связность узлов

i и j с помощью матрицы [(),()]B

kik=

размера 2

m, где m – число ветвей; k – номер ветви, инцидентной

узлам

j и i.

Матрица инциденций [],

=µ

где

= 1, если узел i является началом ветви k;

120

= – 1, если узел i является концом ветви k;

= 0, если узел i и ветвь k неинцидентны;

имеет размер

nm×

, где n число строк, равное числу узлов, а m –

число столбцов, равное числу ветвей. Каждый столбец матрицы

содержит только два отличных от нуля элемента +1 и –1.

6.3. Потоки в сетях

Методика расчета структурной надежности

электроэнергетической системы основывается на теории потоков в

сетях [16]. Расчетная схема электрических соединений энергосистемы

представляется в виде графа (

Y, B). Узлы и ветви графа и схемы

совпадают. Добавим еще два узла: эквивалентный генератор и

эквивалентную нагрузку. На графе они будут представлены узлами

источника

и стока y

. Соединим узел эквивалентного генератора со

всеми генерирующими узлами, а все нагрузочные узлы – с узлом

эквивалентной нагрузки. Соответствующие ветви

и b

на графе

будут ориентированными, в целом же граф смешанный. Пусть

множество генерирующих узлов Г = {2, 3, ... ,

i, ... , r}, а множество

нагрузочных

J = {2, 3, ... , j, ... , s} ( , )i

Г j

∈

∈ .

Заменим неориентированные ветви двумя ветвями,

ориентированными навстречу друг другу. Таким образом, множество

узлов

Y будет включать в себя три подмножества, соответствующие

генерирующим (Г), нагрузочным (Н) и транзитным (Т) узлам, и два

эквивалентных узла 1 и

n. Множества Г и Н пересекаются. Обозначим

через

S(i, j) – поток по ветви (i, j). Каждая ветвь обладает пропускной

способностью

доп

(, )Si

. Любой установившийся поток мощности S

из узла 1 в узел

n S(1–n) должен удовлетворять следующим условиям:

(,) (, ) ,

SIi S jn S==

∑∑

где ,i

Г j

∈

∈ ;

(, ) ( ,) 0,

Si j Shi−=

∑∑

где i Т

∈

;