Гук Ю.Б. Теория надежности. Введение: учеб. пособие

Подождите немного. Документ загружается.

141

- определение компонент связности графа (проверка на деление

системы);

- расчет потокораспределения в сети в целом и в каждом

фрагменте в случае деления (определения максимального потока);

- определение разреза с минимальной пропускной

способностью, вычисление вероятности отказового состояния этого

резерва, вычисление математического ожидания дефицита мощности

(или резерва, если пропускная способность сети не ограничивает

максимальный поток нагрузки), эти же процедуры выполняются в

случае деления сети и для всех фрагментов;

- расчет показателей надежности системы и ее нагрузочных

узлов в рассматриваемом состоянии.

Поведем анализ состояний и оценку надежности для системы,

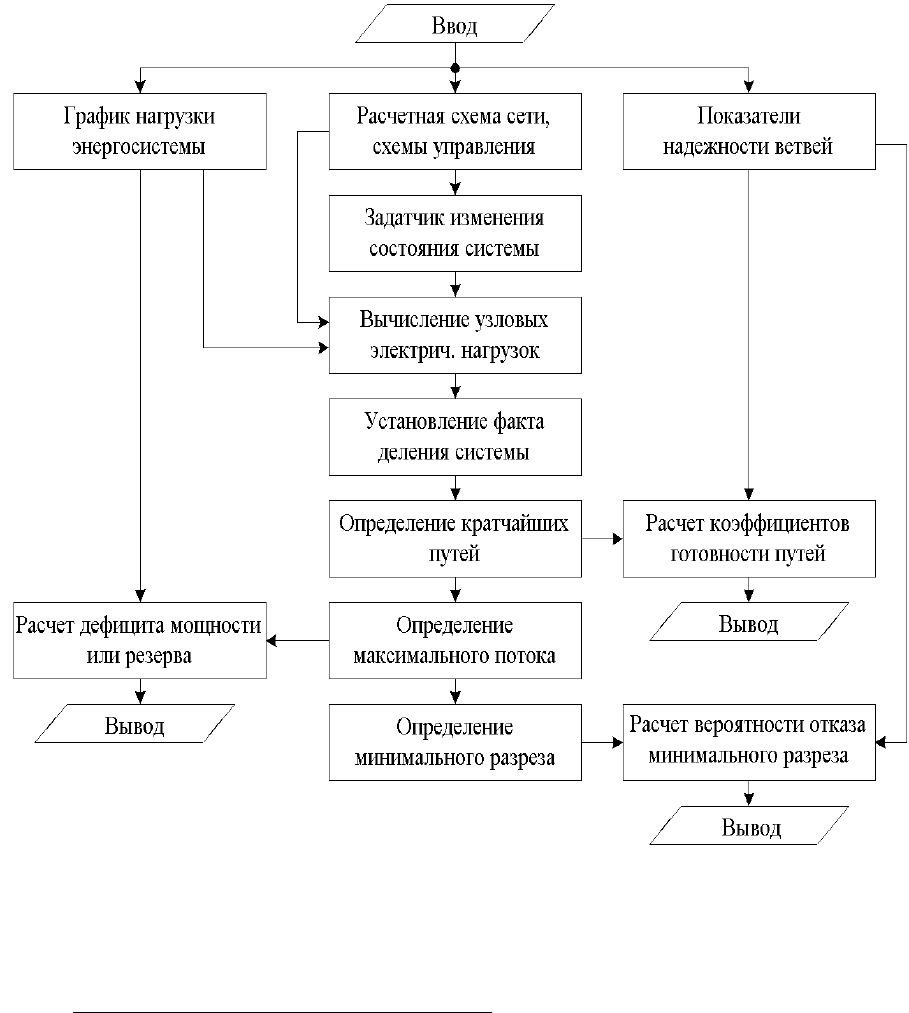
схема которой приведена на рис. 6.6, а граф – на рис. 6.7.

142

Рис. 6.9. Алгоритм исследования состояния системы

Состояние нормального режима

. Схема со всеми включенными

ветвями. Суммарные потоки в генерирующих узлах

S(г) = 800, в

нагрузочных узлах –

S(н) = 800, максимальный поток в сети из узла 1

в 7

max

(1 7) 800S −= .

Дефицит отсутствует:

деф

Минимальный разрез состоит из ветвей

С = {(2,4), (5,7), (2,6), (3,6)}.

143

Вероятность отказового состояния сети

( ) (2,4) (5,7) (2,6) (3,6)

qqcq q q q== .

Задав коэффициенты простоя ветвей пропорционально их

сопротивлениям (длинам), равными:

q(2,4) = 0,001; q(5,7) = 0,002;

q(2,6) = 0,003; q(3,6) = 0,002, получим

1, 2 10

−

=⋅

. Уровень

надежности системы в целом весьма высок, полное погашение

практически невозможно.

Коэффициент возможности для узла нагрузки 4, который

питается по одному пути

= {(1,2), (2,4)}, определяется как

произведение коэффициентов готовности ветвей

(4) (1 0,003)(1 0,001) 0,996003p =− − = .

Коэффициент готовности для узла нагрузки 5, который питается

по двум путям

{(1,2), (2,5)} и D

{(1,5)}, равен

1212

(5) (5) (5) (5) (5) 0,999976pp p pp=+− = ,

где

(5) (1,2) (2,5) (1 0,003)(1 0,002) 0,995006ppp==−−=;

(5) (1,5) 1 0,006 0,994pp==−=.

Коэффициент готовности для узла нагрузки 6:

1212

(6) (6) (6) (6) (6) 0,999934pp p pp=+− = ,

где

(6) (1,2) (2,6) (1 0,003)(1 0,003) 0,994009ppp==−−=;

(6) (1,3) (3,6) (1 0,003)(1 0,008) 0,989024ppp==−−=.

Теперь рассмотрим состояние системы в режиме аварийного

отключения ветви (2,6). Разделение системы на две части в нашем

простейшем случае констатируем без построения покрывающего

дерева. Проверим условия возникновения дефицита в обеих частях

системы.

Часть системы с узлом нагрузки 6.

Здесь (г) 150,S =

max доп

(1 6) (3, 6) 50,SS−= = (н) (6 7) 150.SS

−= Несмотря на избыток

генерирующей мощности, образуется дефицит из-за ограничений по

пропускной способности сети

деф

150 50 100.S

−= Значит, условная

144

вероятность отказа системы в этом состоянии равна 1. Вероятность

отказа системы за счет этого состояния получает составляющую,

равную коэффициенту простоя ветви (2,6), то есть 0,003.

Часть системы с узлами нагрузки 4 и 5

. Здесь S(г) = 800,

max доп доп

(1 7) (4,7) (5,7) 750SSS−= + = , S(н) = 700. Дефицита нет,

имеется резерв

рез max

(1 7) (н) 50.SS S=−−=

Коэффициенты готовности для узлов нагрузки 4 и 5 при

разделении не изменились, так как не изменилось число путей, их

питающих. Коэффициент готовности для узла 6 уменьшился, так как

теперь узел 6 получает питание по одному пути, коэффициент

готовности которого

(6) (1,3) (3,6) 0,989024.ppp

= Кроме того, в

узле 6 есть дефицит.

7. СТАТИСТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ

ЗАДАЧ НАДЕЖНОСТИ

7.1. Сбор статистической информации

Посредством сбора и обработки информации о надежности

изделий промышленности решаются следующие задачи [7, 13]:

определение причин отказов; выявление тех деталей, сборочных

единиц и комплектующих, которые ограничивают надежность

изделия; установление и корректировка нормируемых показателей

надежности; норм расхода запасных частей и системы планово-

предупредительных ремонтов; выявление условий и режимов

эксплуатации, влияющих на надежность; определение экономической

эффективности повышения надежности.

Статистические данные о надежности изделий и оборудования

можно получить либо в результате наблюдений за ними в ходе

нормальной или опытной (подконтрольной) эксплуатации, либо в

результате стендовых испытаний.

145

Наблюдения при нормальной эксплуатации – самый доступный

источник получения экспериментальных данных о надежности. Его

недостатки – запаздывание данных, ограниченные возможности

активного эксперимента, влияние субъективных факторов на объем и

содержание информации.

При опытной эксплуатации наблюдения за работоспособностью

оборудования проводятся с участием представителей служб

надежности, имеющих специальную подготовку и независимых от

воздействия местных субъективных факторов

. Однако ограничения

по времени и числу сотрудников, а также по режиму использования

оборудования не позволяют проводить широкие активные

эксперименты.

Стендовые испытания являются централизованными и

проводятся либо на заводах-изготовителях, либо в специальных

испытательных центрах отрасли. Это весьма дорогостоящий вид

испытаний, осуществляемых не в реальных, а в имитируемых

условиях, отвлекающий значительное

количество продукции от

использования по назначению и продажи. Однако стендовые

испытания дают возможность получить информацию о недостатках

конструкции, технологии и использовать эти данные для повышения

надежности изделий. Стендовые испытания позволяют проводить

активные эксперименты с выявлением слабых мест и проверкой

экстремальных воздействий, а, следовательно, ускорить получение

данных.

Вопросами сбора и обработки информации

о надежности

изделий должны заниматься головные организации отрасли и службы

надежности и качества на предприятиях-изготовителях и

предприятиях-потребителях изделий. Информация о надежности

изделий серийного производства должна собираться с начала их

эксплуатации потребителем. Для изделий, имеющих большой срок

службы и выпускаемых малыми сериями или уникальных,

146

допускается начинать сбор информации с очередного капитального

ремонта или профилактического обслуживания.

Формы документов – носителей информации о надежности

изделий должны быть общими для всех отраслей и соответствовать

действующей нормативно-технической документации. Все формы

подразделяются на первичные формы учета, формы-накопители и

формы записи результатов количественного и качественного анализа.

Например, основные первичные формы

учета: паспорт оборудования;

журнал учета наработок, повреждений и отказов изделий; журнал

технического обслуживания и ремонтов; разовые документы по

эксплуатации изделия потребителем (путевой лист, карточка на

ремонт, донесение об отказе, акт об аварии и т. д.). Все виды форм

должны предусматривать их запись и обработку на ЭВМ.

Порядок заполнения и содержание

донесения об отказе

регламентируется ГОСТ. В донесениях регистрируются отказы

изделий, связанные с опасностью для жизни людей, приводящие к

большим экономическим потерям, а также отказы образцов новой

техники и изделий мелкосерийного и единичного поизводства.

Донесения об отказе заполняется в организации, эксплуатирующей

данное изделие.

В донесении об отказе должны быть следующие данные:

наименование

, марка или тип, заводской номер, предприятие-

изготовитель, ремонтное предприятие, эксплуатирующее

предприятие, дата выпуска, даты ремонтов, дата отказа, адресные

данные отказавших узлов и деталей, наработка, внешние проявления

и характер отказа, причина отказа, условия выявления, последствия

отказа, условия эксплуатации и режимы работы, время

восстановления работоспособности, фактическая трудоемкость

восстановления, исполнители работ по восстановлению.

147

7.2. Испытание на надежность

По своему назначению испытания на надежность бывают

определительными и контрольными. С помощью определительных

испытаний выясняется фактический уровень показателей надежности

для созданного типа изделий, с помощью контрольных

устанавливается соответствие испытуемой партии изделий заданным

(нормируемым) требованиям. Контрольные испытания применяются

для входного контроля комплектующих изделий и выходного

контроля выпускаемой продукции.

По объему выборки

различают испытания с полной и неполной

(усеченной) выборкой. Испытания с полной выборкой проводятся до

отказа всех испытуемых изделий. При неполной выборке испытания

проводятся либо в течение заданного времени, либо до

возникновения определенного числа отказов, либо до достижения

заданной наработки.

При массовом производстве нет возможности для тщательной

проверки каждого изделия. При

мелкосерийном производстве такая

проверка может быть экономически нецелесообразной, особенно если

многие свойства изделия обеспечиваются при монтаже установки

после длительной транспортировки и хранения. В этом случае

проводится выборочный статистический контроль качества и

надежности, когда о генеральных (присущих всей партии изделий)

совокупностях судят на основании характеристик, определяемых по

малой выборке из партии.

Статистический

контроль качества и надежности может

производиться либо в процессе производства (так называемый

текущий предупредительный контроль), либо по окончании

производства (так называемый приемочный котроль). Приемочный

контроль может осуществляться у изготовителя (выходной контоль) и

у потребителя изделий (входной контроль). Существует три наиболее

распространенных метода приемочного контроля: метод однократной

148

выборки, метод двукратной выборки и метод последовательных

испытаний.

Метод однократной выборки рекомендуется для испытаний

опытных образцов техники, когда объем испытаний (число образцов

и продолжительность испытаний) задается заранее. При методе

однократной выборки из контролируемой партии отбирается

случайным образом определенное число изделий (выборка). По

оценкам показателей надежности или качества этой выборки

принимается решение

о том принимать ли данную партию изделий

или забраковать её, отправив на сплошной контроль или на

переделку.

Метод двукратной выборки заключается в том, что в случае

сомнения в качестве или надежности по результатам испытаний

выборки, производят вторую выборку из партии, и уже по

характеристикам обеих партий принимают решение о приемке

или

браковке.

Метод последовательных испытаний обеспечивает значительно

меньший средний объем испытаний, чем два первых метода и

поэтому применяется при испытаниях массовой серийной продукции.

На испытания ставится несколько изделий и регистрируется

суммарная наработка и число отказов. Испытания продолжаются до

того момента, когда либо число отказов превысит предельное

значение (браковка партии), либо суммарная

наработка превысит

предельное значение, а число отказов не достигнет браковочного

числа (приемка партии). При этом можно добавлять изделия для

испытания, если они затянулись.

При планировании испытаний на надежность необходимо

задать следующее:

• признаки или критерии отказа изделий;

• показатель надежности, который является определяющим для

данного изделия;

149

• условия испытаний (электрические параметры, климатические

условия, механические нагрузки, последовательность и длительность

режимов);

• способ контроля работоспособности (обычный

эксплуатационный или специальный испытательный, непрерывный

или периодический);

• способ замены отказавших изделий (отказавшие изделия не

заменяются до конца испытаний – план типа

U, заменяются

немедленно после отказа – план типа

R, восстанавливаются в ходе

испытаний – план типа

M);

• число испытуемых изделий N;

• правило окончания испытаний (по истечению заданного

времени

T, после наступления r-го отказа, по истечению суммарной

по всем объектам наработки или времени

, после отказа всех

изделий).

Для обозначения планов испытаний применяется символика с

тремя позициями: число испытуемых изделий, способ замены

отказавших и правило окончания испытаний. Например: [

NUN] –

испытания

N изделий без замены отказавших до отказа всех изделий,

[

NR(rT

)] – испытания N изделий с заменой отказавших до

достижения суммарной наработки

или r

отказов.

В ГОСТ 27.502-83 приводятся формулы для определения

минимального числа объектов наблюдения при известном законе

распределения исследуемой случайной величины (экспоненциальном,

нормальном, Вейбулла и логарифмически нормальном), при этом

задаются доверительной вероятностью

β и относительной ошибкой δ

в оценке среднего значения случайной величины.

При экспоненциальном законе распределения наработки на

отказ число объектов N должно удовлетворять выражению

150

(1 , 2 )

=+δ

χ−β

;

вср

ср

−

δ=

;

где

(1 – β; 2N) – квантиль распределения хи-квадрат при числе

степеней свободы 2

N; t

– верхняя доверительная граница; t

ср

–

среднее значение наработки на отказ.

При неизвестном виде закона распределения случайной

величины минимальное число

N для проверки требуемой вероятности

P(t

) с доверительной вероятностью β задается из условия отсутствия

отказов за время

ср

ln(1 )

ln ( )

−

Если при испытаниях

N объектов за время t

не будет отмечено

ни одного отказа, результаты испытаний считаются

удовлетворительными. Если же произойдет хотя бы один отказ, то

требуемое значение вероятности не подтверждается.

Пример 7.1. Определим объем испытаний дизель-генераторов

для аварийного источника электроснабжения. Заданная вероятность

безотказной работы

P(t

) = 0,9 в течение расчетного времени

ликвидации аварии

= 240 ч.

Приняв доверительную вероятность того, что

P(t

) ≥ 0,9, равной

0,95, получим

ln(1 0,95)

28,43.

ln 0,9

−

Это означает, что на испытания в течение 240 часов надо

поставить 30 дизель-генераторов. Если за это время не произойдет ни

одного отказа, то

P(240) ≥ 0,9. В противном случае P(240) < 0,9.

Допустим, что было 5 отказов, тогда точечная оценка вероятности

P(240) = (30 – 5)/30 = 0,833.