Гук Ю.Б. Теория надежности. Введение: учеб. пособие

Подождите немного. Документ загружается.

121

доп

(, ) (, )Si

≤ .

Пропускная способность ветвей (1, i) соответствует

располагаемым мощностям

расп

i-ыx генераторных узлов, а ветвей

(j, n) – мощностям нагрузки S

j-ыx нагрузочных узлов.:

расп

(1, ) , ;

Si S i

≤∈

(,) , .

Sjn S j H

∈

Ограничения для ветвей с реверсом перетока:

доп

(, ) (, );Si

≤

доп

(,) (,);S

i≤ (, ) ( ,) 0,Si j S ji

⋅

то есть поток допустим только в одном направлении.

Вышеприведенные условия учитывают только первый закон

Кирхгофа при расчете потокораспределения в сети. Поставим задачу

поиска максимально возможного потока от источника к стоку.

Согласно [16] максимальная величина возможного потока

max

(1 )Sn

−

равна минимальной пропускной способности разреза, отделяющего

источник от стока. Разрез с минимальной пропускной способностью

min

(, )SRR содержит ветви, которые ограничивают пропускную

способность путей (1–n). Следует отметить, что между любыми двумя

узлами графа существует некоторое множество D(i–j) путей, объем

которого определяется структурой графа.

Поток по пути D

(i–j), будем обозначать S

(i–j). Тогда

суммарный поток из узла 1 в n

(1 ) (1 ).

Sn S n

−

=−

∑

Потоки по пути

ограничиваются потоками отдельных ветвей S(i, j), составляющих

данный путь. С одной стороны, так как ветвь может входить в

несколько путей между одними и теми же узлами, то

доп

(1 ) ( ).

ik k i

SnSbµ−≤

∑

Здесь i = 1, 2, ... , m; где m – количество ветвей графа; k = 1, 2, ...

, d, где d – количество путей из узла 1 в n; µ

– элементы матрицы

инциденций ветви-пути. С другой стороны, поток по пути ограничен

122

той ветвью из всей цепочки составляющих его ветвей, поток по

которой минимален:

(1 ) min ( ).

Sn Sb

∈

−=

6.4. Поиск кратчайшего пути

Каждая ветвь графа может быть охарактеризована своим

коэффициентом, отражающим длину, стоимость, сопротивление и

другие характеристики реальной сети. Коэффициенты всех ветвей в

частном случае могут быть равны. Под кратчайшим путем будем

понимать путь с минимальным сопротивлением, считая, что каждая

ветвь графа имеет сопротивление Z(i, j). Алгоритм определения

кратчайшего пути предусматривает последовательное

отыскивание

всех путей от источника к стоку и сравнение их сопротивлений [17].

Основная идея поиска заключается в построении дерева кратчайших

путей (минимальных сопротивлений) с корнем в истоке графа с

постепенным окрашиванием узлов и ветвей до тех пор, пока не

окрасится сток. Наращивание дерева (окрашивание) производится по

результатам сравнения суммарных сопротивлений от

истоков до

рассматриваемых узлов. В процессе поиска пути узлы графа могут

быть окрашенными и неокрашенными, в свою очередь неокрашенные

узлы могут быть просмотренными, просматриваемыми и не

просмотренными.

Исходное состояние – все узлы не окрашены за исключением

источника. Просматриваем узлы, смежные источнику. Определяем

сопротивления от источника до просматриваемых узлов.

Сопротивления эти равны сопротивлениям

ветвей Z(1, i), где i –

просматриваемые узлы. Окрашиваем узел, сопротивление до которого

минимально, а ветвь, соединяющую окрашиваемый узел с истоком.

Далее просматриваются узлы i, смежные последнему

окрашенному узлу. Определяются сопротивления Z(1–i) путей от

123

источника до этих узлов. Сравниваются сопротивления путей от

источника до просматриваемых узлов и до просмотренных, но не

окрашенных на предыдущих шагах. Выбирается из них минимальное.

Окрашивается узел, сопротивление до которого минимально, а ветвь,

участвующая в формировании пути, имеет минимальное

сопротивление и т. д. Процесс прекращают, когда будет окрашен сток

или когда

будут окрашены все узлы, а сток не достигнут (отсутствие

стока).

Путь от источника к стоку по окрашенным ветвям и узлам будет

путем с минимальным сопротивлением. Этот путь единственный, так

как остальные ветви построенного дерева тупиковые.

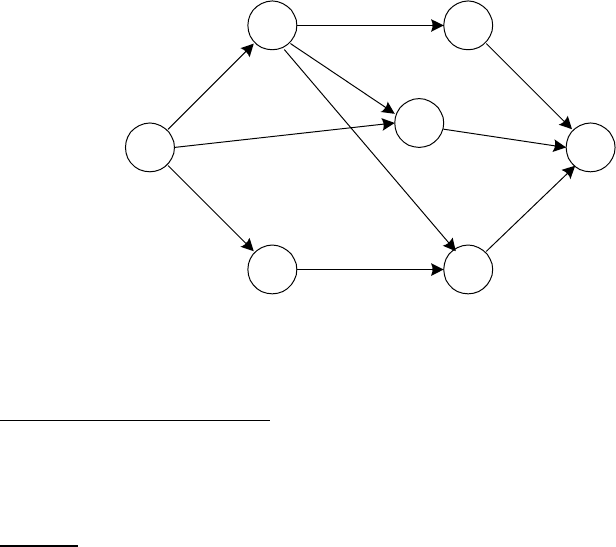
На рис. 6.1 представлен граф некоторой сети с указанными

сопротивлениями ветвей. Найдем кратчайший путь из узла 1

в узел 7.

1 7

3 6

Рис. 6.1. Граф системы с весами ветвей

Исходное состояние.

Окрашиваем узел 1 как источник и корень

дерева. Обозначим последний на данном этапе окрашенный узел

через Н.

Шаг1.

При Н = 1 просматриваем сопротивления до смежных

узлов (рис. 6.1):

Z(1, 2) = Z(1–2) = 3;

Z(1, 5) = Z(1–5) = 6;

124

Z(1, 3) = Z(1–3) = 3.

Минимальное сопротивление от источника до узлов 2 и 3.

Следовательно, узлы 2 и 3 надо окрасить вместе с ветвями (1, 2) и

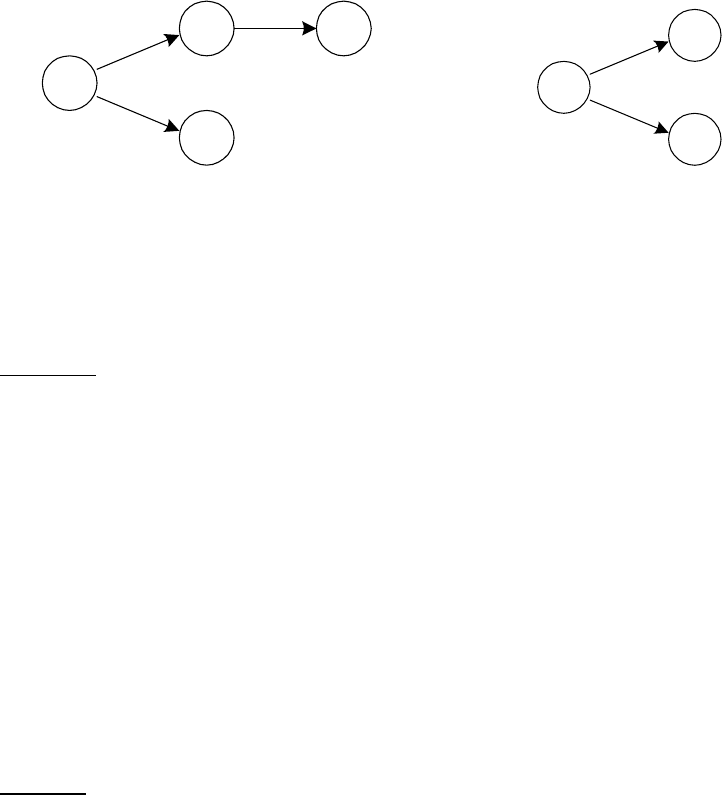
(1, 3). На рис. 6.2 показано окрашенное на первом шаге дерево.

Рис. 6.2. Шаг 1 поиска

кратчайшего пути

Рис. 6.3. Шаг 2 поиска

кратчайшего пути

Шаг 2.

Просматриваем сопротивление до узлов, смежных с

узлами Н.

При Н = 2

Z(1–4) = 4,

Z(1–5) = 5,

Z(1, 5) = 6 (просмотренное ранее на шаге 1),

Z(1–6) = 6.

При H = 3 Z(1–6) = 5. Минимальное сопротивление до узла 4,

его и окрашиваем вместе с ветвью (2, 4). Окрашенное дерево

принимает вид, показанный на рис. 6.3.

Шаг 3.

При Н = 4 Z(1–7) = 8,

При Н = 2 Z(1–6) = 6, Z(1–5) = 5.

При Н = 3 Z(1–6) = 5.

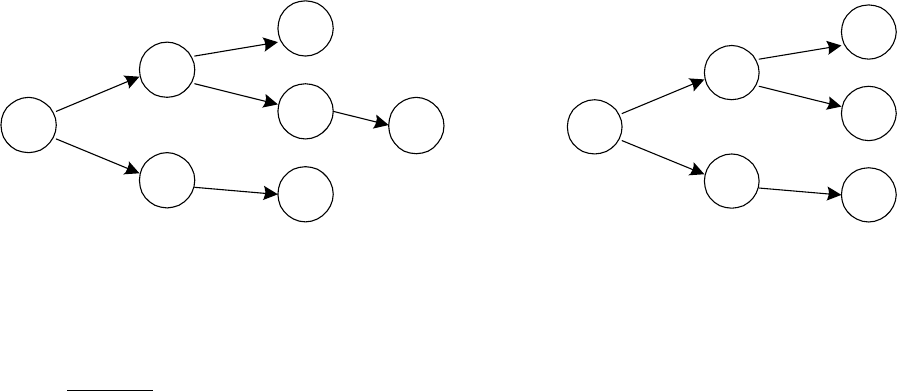
Окрашиваем узлы 5 и 6 и ветви (2, 5) и (3, 6). После этого

окрашенное дерево принимает вид, показанный на рис. 6.4.

125

Рис. 6.4. Шаг 3 поиска

кратчайшего пути

Рис. 6.5. Шаг 4 поиска

кратчайшего пути

Шаг 4.

При Н = 4 Z(1–7) = 8.

При Н = 5 Z(1–7) = 7.

При Н = 6 Z(1–7) = 9.

Окрашиваем узел 7 и ветвь (5, 7). Так как узел 7 окрашен, то

задача решена. Окрашенное дерево показано на рис. 6.5. Кратчайший

путь (1–7) = {(1, 2), (2, 5), (5, 7)}.

6.5. Поиск пути, увеличивающего поток

Все ветви графа в зависимости от текущей нагрузки и

ограничений по пропускной способности можно отнести к одной из

трех категорий; 1) ветви, по которым поток нельзя ни увеличить, ни

уменьшить; 2) ветви, поток по которым можно увеличить; 3) ветви, по

которым поток можно уменьшить. В дальнейшем будем называть

ветви нейтральными, увеличивающими и уменьшающими и

относить

к множествам В°, В

, В

−

соответственно. Множества В

и В

−

могут

быть пересекающимися (поток по ветви можно и увеличить и

уменьшить). Обозначим максимальную величину, на которую можно

увеличить и уменьшить поток по ветви через S

(i, j) и S

−

(i, j)

соответственно. Очевидно, что в любом

режиме

(i, j) = S

доп

(i, j) – S(i, j) и S

–

(i, j) = S(i, j).

126

В отсутствии потоков по ветвям (перед началом процесса

распределения потоков по ветвям) S

(i, j) = S

доп

(i, j).

Процесс определения максимального потока S(1–n) включает в

себя поиск пути, по которому можно увеличить поток

(1 )

−

(увеличивающего пути). Рассмотрим три возможных на практике

случая.

1) Если путь состоит из прямых ветвей, то увеличивающий путь

определяется из условия

(, )

(1 ) min { ( , )}

ij D

Sn Sij

∈

−= .

2) Если путь содержит только обратные ветви, то

(, )

(1 ) min { ( , )}

ij D

Sn Sij

+−

∈

−= .

3) Если путь содержит прямые и обратные ветви, то

увеличивающий путь определяется из условия

(, ) ( , )

(1 ) min min { (1, )}, min { ( , )}

ij D hd D

Sn Sj Shd

++−

∈∈

⎡⎤

−=

⎢⎥

⎣⎦

где (i, j) – прямые ветви; (h, d) – обратные ветви.

6.6. Алгоритм поиска максимального потока

Алгоритм поиска максимального потока содержит две основные

операции, которые выполняются последовательными шагами до

достижения результата.

Шаг 1. В исходном состоянии для всех ветвей принимается

значение потока S(i, j) = 0 (операция О

Шаг 2. Выполняется операция О

. Определяются возможности

увеличения и уменьшения потока по всем ветвям:

(i, j) = S

доп

(i, j) – S(i, j) и S

–

(i, j) = S(i, j)

и тем самым выявляется отношение ветвей к множествам В°,

, В

−

127

При первом обращении к операции О

все ветви относятся к

множеству В

(увеличивающих поток ветвей), и ни одна из них не

относится к множеству В

–

или В

, так как S(i, j) = 0.

Шаг 3. Выполняется операция О

. Отыскивается кратчайший

путь из источника в сток и определяется максимальное увеличение

потока по D

(1–n) найденному кратчайшему пути. При этом

используются алгоритмы, описанные в двух предыдущих разделах.

Если увеличение потока по кратчайшему пути возможно S

(1–n)

> 0, то на шаге 4 выполняется операция О

, а затем на шаге 5 –

операция О

. И до тех пор, пока удается найти увеличивающий поток,

продолжается чередование шагов с операциями О

и О

Если увеличивающий поток найти не удается, то поиск

прекращается. Ветви, упирающиеся одним концом в окрашенный

узел, а другим в неокрашенный, являются минимальным разрезом

графа. Максимальный поток вычисляется как сумма потоков по всем

ветвям минимального разреза.

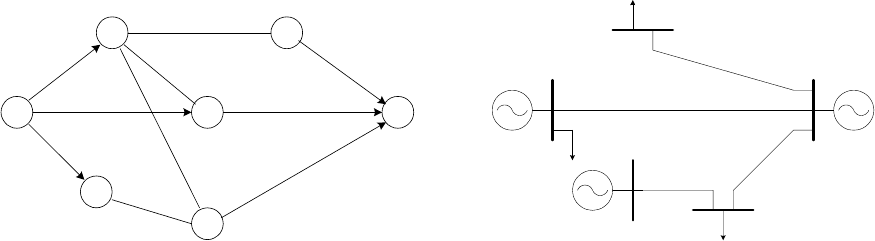
В качестве примера рассмотрим электрическую систему, схема

которой приведена на рис. 6.6. Соответствующий этой схеме граф

показан на рис. 6.7. Рядом с ветвями указаны их пропускные

способности.

5 7

550

200

300

250

100

450

100

150

250

Рис. 6.6. Пример простейшей

электрической системы

Рис. 6.7. Граф системы с

пропускными способностями

ветвей

128

Найдем максимальный поток на этом графе с помощью

алгоритмов поиска кратчайшего пути и пути, увеличивающего поток,

и указанных выше операций.

Шаг 1. Операция О

. Примем все потоки в ветвях равными

нулю: S(i, j) = 0.

Шаг 2. Операция О

. Каждая ветвь относится к множеству В

так как S(i, j) < S

доп

(i, j), а S

(i, j) = S

доп

(i, j) – S(i, j) и ни одна из

ветвей не может быть отнесена к множеству В

–

, так как S(i, j) = 0, а

–

(i, j) = S(i,

j). Следовательно, S

(i, j) = S

доп

(i, j) и S

–

(i, j) = 0.

Шаг 3. Операция О

. Найдем кратчайший путь из 1 в 7. В

предыдущем примере такой путь (1 – 7) найден: {(1,2), (2,5), (5,7)}.

Максимальное увеличение потока по этому пути составляет

min{S

(1,2), S

(2,5), S

(5,7)} = min(550, 300, 450) = 300. В данном

пути ветвь (2,5) ограничивает поток. Следовательно, S(1,2) = S(2,5) =

= S(5,7) = 300. Во всех других ветвях поток пока принимается равным

нулю.

Шаг 4. Операция О

. Корректируется состав множеств В

и В

–

- увеличивающий поток ветви (1,2):

(1,2) = S

доп

(1,2) – S(1,2) = 550 – 300 = 250;

- уменьшающий поток по ветви (1,2)

–

(1,2) = S(1,2) = 300.

Ветвь (1,2) относится к множеству В

и к В

, то есть (1,2)∈В

(1,2)∈В

–

. Аналогично для других ветвей.

(2,5) = 300 – 300 = 0, (2,5)∉B

;

–

(2,5) = 300, (2,5)∈B

–

;

(5,7) = 450 – 300 = 150, (5,7)∈

;

–

(5,7) = 300, (5,7)∈B

–

129

Увеличивающие потоки по остальным ветвям равны их

допустимым пропускным способностям, а уменьшающие потоки

равны нулю.

Шаг 5. Операция О

. Найдем кратчайший путь из 1 в 7,

учитывая, что по ветви (2,5) поток увеличить нельзя. Таким путем

является {(1,5), (5,7)}. Максимальное увеличение потока по этому

пути составляет

min{S

(1,5); S

(5,7) = min{250,150} = 150.

Теперь по ветвям графа устанавливаются следующие потоки:

S(1,5) = 150, S(5,7) = 300 + 150 = 450, S(1,2) = S(2,5) = 300,

S(1,3) = S(3,6) = S(2,6) = S(6,7) = S(4,7) = 0.

Шаг 6. Операция О

. Пересчитываются значения S

(i, j) и S

–

(i, j)

для новых значений потоков в ветвях. Корректируется состав

множеств В

и В

–

. Для ветвей с нулевыми значениями потоков имеем

S(2,5) = 300 = S

доп

(2,5); (2,5)∉B

; (2,5)∈B

–

; S

–

(2,5)=300;

S(1,2) = 300 < S

доп

(1,2); (1,2)∈B

; S

(1,2) = 250; (1,2)∈B

–

;

–

(1,2) = 300.

S(5,7) = 450 = S

доп

(5,7); (5,7)∉B

; (5,7)∈B

; S

(5,7) = 450;

S(1,5) = 150 < S

доп

(1,5); (1,5)∈B

; S

(1,5) = 100; (1,5)∈B

;

(1,5) = 150.

Шаг 7. Операция О

. Найдем кратчайший путь, увеличивающий

поток

из 1 в 7, с учетом нового потокораспределения. Таким путем

является {(1,2) (2,4), (4,7)}. Максимальное увеличение потока по

этому пути

min{S

(1,2), S

(2,4), S

(4,7)} = min{250, 200, 250} = 200.

По ветвям рассматриваемого пути устанавливаются следующие

значения потоков: S(1,2) = 300 + 200 = 500; S(2,4) = S(4,7) = 200.

Шаг 8. Операция О

. Изменения возможностей увеличения и

уменьшения потоков выглядят теперь так:

130

S(1,2) = 500 < S

доп

(1,2); (1,2)∈B

; S

(1,2)=50; (1,2)∈B

–

;

–

(1,2) = 500;

S(2,4) = 200 = S

доп

(2,4); (2,4)∉B

; (2,4)∈B

–

; S

–

(2,4) = 200;

S(4,7) = 200 < S

доп

(4,7); (4,7)∈B

; S

(4,7) = 50; (4,7)∈B

–

;

–

(4,7) = 200.

Шаг 9. Операция О

. Кратчайший путь, увеличивающий поток

на данном шаге, {(1,3),(3,6),(6,7)}. Максимальное увеличение потока

по этому пути

min{S

(1,3), S

(3,6), S

(6,7) = min{100, 50, 150} = 50.

Следовательно, S(1,3) = S(3,6) = S(6,7) = 50.

Шаг 10. Операция О

. Имеем

S(1,3) = 50 < S

доп

(1,3); (1,3)∈B

; S

(1,3) = 50; (1,3)∈B

–

;

–

(1,3) = 50.

S(3,6) = 50 = S

доп

(3,6); (3,6)∉B

; S

(3,6) = 0; (3,6)∈B

–

;

–

(3,6) = 50;

S(6,7) = 50 < S

доп

(6,7); (6,7)∈B

; S

(6,7) = 100; (6,7)∈B

–

;

–

(6,7) = 50.

Шаг 11. Операция О

. Путь, увеличивающий поток {(1,2), (2,6),

(6,7)} до максимального значения,

min{S

(1,2), S

(2,6), S

(6,7)} = min{50, 100, 100} = 50.

Шаг 12. Операция О

. По всем ветвям имеем

S(1,2) = 550 = S

доп

(1,2); (1,2)∉B

, S

(1,2) = 0, (1,2)∈B

–

(1,2) = 550;

S(2,6) = 50 < S

доп

(2,6), (2,6)∈B

, S

(2,6) = 50, (2,6)∈B

–

(6,7) = 100;

S(1,5) = 150 < S

доп

(1,5), (1,5)∈B

, S

(1,5) = 100, (1,5)∈B

–

(1,5) = 150;