Гук Ю.Б. Теория надежности. Введение: учеб. пособие

Подождите немного. Документ загружается.

131

S(1,3) = 50 < S

доп

(1,3), (1,3)∈B

, S

(1,3) = 50, (1,3)∈B

–

(1,3) = 50;

S(2,4) = 200 = S

доп

(2,4), (2,4)∉B

, S

(2,4) = 0, (2,4)∈B

–

(2,4) = 200;

S(2,5) = 300 = S

доп

(2,5), (2,5)∉B

, S

(2,5) = 0, (2,5)∈B

–

(3,6) = 50;

S(4,7) = 200 < S

доп

(4,7), (4,7)∈B

, S

(4,7) = 50, (4,7)∈B

–

(4,7) = 200;

S(5,7) = 450 = S

доп

(5,7), (5,7)∉B

, S

(5,7) = 0, (5,7)∈B

–

(5,7) = 450.

Шаг 13. Операция О

. Увеличить поток можно только по пути

{(1,5), (5,2), (2,6), (6,7)}, причем для ветви (5,2) используется

возможность уменьшения потока по ветви (2,5). Максимальное

увеличение потока по этому пути:

min{S

(1,5), S

–

(2,5), S

(2,6), S

(6,7)} =

= min{100, 300, 50, 50} = 50.

По ветвям рассматриваемого пути устанавливаются следующие

потоки S(1,5) = 200; S(2,5) = 300 – 50 = 250; S(2,6) = 150. Уменьшение

потока по ветви (2,5) приводит к уменьшению потока по пути {1,2),

(2,5), (5,7)} с 300 до

250. В итоге, к настоящему шагу потоки

распределяются следующим образом:

по пути {(1,2), (2,4), (4,7)} S = 200;

по пути {(1,2), (2,5), (5,7)} S = 250;

по пути {(1,2), (2,6), (6,7)} S = 100;

по пути {(1,5), (5,7)} S = 200;

по пути {(1,3), (3,6), (6,7)} S = 50.

Шаг 14. Операция О

. По всем ветвям имеем

132

S(1,2) = 550 = S

доп

(1,2), (1,2)∉B

, S

(1,2) = 0, (1,2)∈B

–

(1,2) = 550;

S(1,5) = 200 < S

доп

(1,5), (1,5)∈B

, S

(1,5) = 50, (1,5)∈B

–

(1,5) = 200;

S(1,3) = 50 < S

доп

(1,3), (1,3)∈B

, S

(1,3) = 50, (1,3)∈B

–

(1,3) = 50;

S(2,4) = 200 = S

доп

(2,4), (2,4)∉B

, S

(2,4) = 0, (2,4)∈B

–

(2,4) = 250;

S(2,6) = 100 = S

доп

(2,6), (2,6)∉B

, S

(2,6) = 0, (2,6)∈B

–

(2,6) = 100;

S(3,6) = 50 = S

доп

(3,6), (3,6)∉

, S

(3,6) = 0, (3,6)∈B

–

(3,6) = 50;

S(4,7) = 200 < S

доп

(4,7), (4,7)∈B

, S

(4,7) = 50, (4,7)∈B

–

(4,7) = 200;

S(5,7) = 450 = S

доп

(5,7), (5,7)∉B

, S

(5,7) = 0, (5,7)∈B

–

(5,7) = 450;

S(6,7) = 150 = S

доп

(6,7), (6,7)∉B

, S

(6,7) = 0, (6,7)∈B

–

(6,7) = 150.

Шаг 15. Операция О

. заканчивается неудачей, так как найти

путь, увеличивающий поток из 1 в 7, при сложившемся

распределении не удается. В процессе выполнения шага 15 в

исходном графе оказались окрашенными узлы 1, 2, 3 и 5. Узел 7 не

окрашивается. Поиск максимального потока прекращается.

Максимальная величина потока определяется как сумма найденных

потоков по ветвям, связанным со стоком,

S(4,7) + S(5,7) + S(6,7) = 800.

133

Используем последний шаг для нахождения максимального

разреза. Отнесем все окрашенные узлы к множеству R, а все

неокрашенные – к

R . Тогда ветви, соединяющие узлы из множества R

R , будут входить в минимальный разрез. В нашем случае

R = {1,2,3,5},

= {4,6,7}.

Ветви, начальные узлы которых окрашены, а конечные не

окрашены, составляют разрез {(2,4), (5,7), (2,6), (3,6)}, называемый

минимальным. Пропускная способность этого разреза равна

доп

(2,4) + S

доп

(5,7) + S

доп

(2,6) + S

доп

(3,6) =

= 200 + 450 + 100 + 50 = 800.

Это значение совпадает с найденным раннее максимальным

потоком из 1 в 7. Из этого следует, что данная сеть не ограничивает

поток из источника в сток.

6.7. Вычисление показателей надежности электрической

системы

Вероятность отказа системы может быть определена по

формуле полной вероятности (теореме гипотез), если в качестве

вероятностей гипотез принять относительные длительности

состояний, различающиеся схемой сети, уровнем генерации и

уровнем потребления мощности, а в качестве условных вероятностей

отказа системы – относительные длительности дефицита мощности в

системе в целом, в каком-либо из ее фрагментов

или в каком-либо

узле. Возникновение дефицита мощности будем считать аварией, вид

аварии в зависимости от места возникновения и величины дефицита

(считая полное погашение узла 100%-ным дефицитом) обозначим

индексом k. Каждому состоянию системы, в котором может

возникнуть авария любого вида, присвоим индекс l. Выражение для

вероятности аварии k-го вида

q(k) можно записать как

() ( )

()

qk pqkl

∑

134

где p

– относительная длительность состояния l;

q(k|l) – условная вероятность нахождения в аварийном режиме

k-го вида в состоянии l;

– множество состояний системы;

N(E

) – количество элементов множества E

В общем случае, если каждый элемент системы может

находиться в двух состояниях (работы или восстановления), то

N(E

) ≥ 2

, где n – число элементов системы. Если элементы кроме

указанных двух состояний могут быть еще и в состоянии резерва или

профилактического обслуживания, то число возможных состояний

системы становится практически необозримым.

Чтобы ограничить число рассматриваемых состояний, не

учитывают маловероятные состояния. Так, при использовании метода

минимальных сечений для расчета надежности узлов нагрузки в [10]

предлагается учитывать только одно- или двухэлементные сечения.

Отдельные состояния, однако, могут быть описаны достаточно

строго как в отношении схемы сети, так и по режиму генерирования,

передачи и потребления мощности. Поэтому анализ надежности

электрической системы в конкретном состоянии (режиме)

представляет собой вполне четкую задачу.

Отказ системы в состоянии l определяется располагаемой

генерирующей

мощностью, пропускной способностью сети и

графиком нагрузки. Примем такую модель нагрузки, при которой все

нагрузки в узлах изменяются пропорционально суммарному графику

нагрузки системы (нагрузки коррелированы). Для каждого состояния

системы существует предельный максимальный поток

(

)

доп max

SS n=−,

определяемый пропускной способностью сети и располагаемой

генерирующей мощностью. Если нагрузка потребителей системы

135

потр

, заданная суточным графиком, превышает

доп

, то система

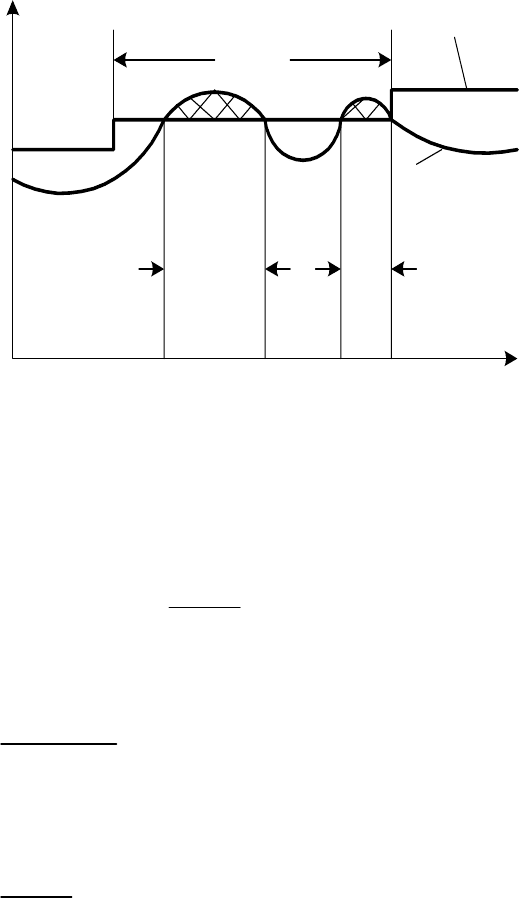
отказывает. На рис. 6.8 показано изменение

доп

потр

во времени.

доп

потр

Рис. 6.8. График предельного потока мощности и потребления

системы

Условная вероятность отказа системы в состоянии l определится

статистически как

()

qkl

∑

;

частота отказов

()

tdi

λ=

−

∑

;

интенсивность восстановления

()

µ=

∑

Вычислить вероятность отказа системы (

k-й аварии) в каком-

либо состоянии аналитически можно с помощью рассмотренных

выше сетевых моделей.

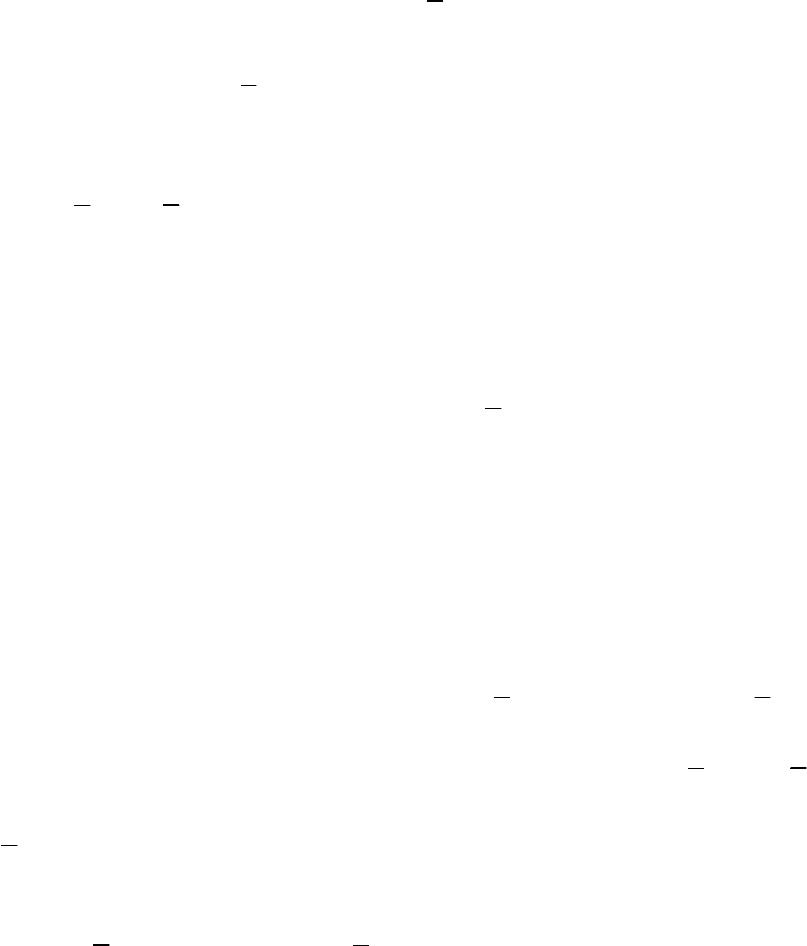
136

Обозначим через D работоспособное состояние системы. Самой

тяжелой аварией является полное прекращение электроснабжения

всех потребителей системы –

D , которая наступает тогда, когда

отказывают все элементы какого-либо из минимальных сечений

системы (событие

). Тогда, учитывая возможные сочетания отказов

всех

m минимальных сечений системы,

В этом случае необходимо на графе сети определить все

минимальные сечения, отделяющие источник от стока. Максимальная

величина потока из источника в сток равна пропускной способности

минимального разреза графа

(, )CRR, который содержит ветви,

ограничивающие пропускную способность путей. Вероятность

отказового состояния системы из-за отказа минимального разреза

является вероятностью полного прекращения электроснабжения

()

(

)

qqC qij==

∏

где

(i, j) – вероятность отказового состояния r-й ветви,

входящей в минимальный разрез

(, )CRR, rC

∈

, iR

∈

R∈ .

Для аварии с прекращением питания

k-го узла

kjk

, где

,jk

все минимальные сечения, отделяющие источники питания от k-

ого узла. Обесточивание узла из-за отказа минимального разреза

()

kkk

CRR k-ого узла

(, )

krk

Dij

. Здесь

(, )

– ветви

минимального разреза

k-ого узла. Вероятность такой аварии

(

)

()

(

)

krk

qk qC q ij==

∏

137

где

(

)

qij – вероятность отказового состояния r-й ветви,

входящей в минимальный разрез

(

)

kkk

CRR,

∈

iR∈ ,

R∈ .

Другой способ вычисления вероятностей аварий системы

заключается в определении коэффициентов готовностей путей.

Обозначим коэффициент готовности пути

D через

(

)

Kp= , тогда

() ( )

Dpij=

∏

где

(

)

ij – коэффициент готовности s-й ветви, входящей в

путь

Вероятность безотказной работы всех путей, составляющих

максимальный поток для системы в целом, определить точно

затруднительно ввиду большого количества путей. Однако, в случае

рассмотрения надежности электроснабжения отдельного узла

нагрузки число путей

i, по которым распределен поток мощности,

невелико и

,kik

DD=

. Определив коэффициент готовности каждого

пути, можно вычислить коэффициент готовности для системы

электроснабжения узла по известным формулам теории вероятностей:

в случае одного пути:

() ( )

kpD= ;

в случае двух путей

() ( ) ( )

(

)

(

)

1212

kpD pD pDpD=+− ;

в случае трех путей

()

1231223

13 123

() () () ()( ) ( )()

()() ()()().

pk pD p D pD pD pD pD pD

pD pD pD pD pD

=+ +− − −

−+

Вероятность аварий определится как

() 1 ()qk pk

−

В каждом состоянии системы, как в аварийном, так и в

послеаварийном режиме, надежность может характеризоваться

возникновением дефицита мощности и недоотпуска электроэнергии

138

за время существования этого состояния. Дефицит мощности

возникает в системе, если

()

max

(1 )SH S n>− или () (г)SH S> ,

где

S(H) – суммарный поток нагрузочных узлов;

max

(1 )Sn− –

максимальный поток сети, определяемый ее пропускной

способностью;

S(г) – поток генерирующих узлов. Дефицит мощности

в каждый

t-й час графика нагрузки в l-м состоянии системы

деф

() (г)

lt lt

SSHS=−

, или

деф

max

() (1 ).

lt l

SSHS n

−−

Недоотпуск электроэнергии за расчетное время существования

состояния определится суммированием дефицитов мощности за

соответствующие часы

деф

WS∆=

∑

;

суммируя недоотпуск энергии по всем состояниям года работы

системы, можно получить среднегодовой недоотпуск энергии

WW∆=∆

∑

Если суммарная мощность нагрузочных узлов меньше

max

(1 )

Sn−

, можно говорить о запасе (избыточности) l-го состояния

системы

рез

max

(1 ) ( )

SS nSH=−−

6.8. Алгоритм анализа состояний системы

Одним из актуальных вопросов структурного анализа

электроэнергетических систем является исследование множества

возможных состояний. Любое возмущение, будь то внешнее или

внутреннее, вызывает в энергосистеме ответную реакцию – действия

устройств управления, в качестве которых выступают различные

устройства автоматики и релейной защиты.

139

При срабатывании таких устройств может происходить

отключение (включение) одновременно одного или нескольких

элементов системы. Например, от действия устройств резервирования

отказавшего выключателя (УРОВ) может отключиться несколько

линий, отходящих от узла. Включения и отключения элементов могут

осуществляться и по команде диспетчера, особенно в условиях

ликвидации аварии.

Изменение структуры системы вследствие действия средств

управления

порождает множество состояний. При этом может

происходить деление системы на несколько частей. В этом случае

необходимо анализировать каждую выделившуюся часть на

сбалансированность генерации и потребления.

Факт деления или целостности системы в каком-либо состоянии

устанавливается с помощью алгоритма построения покрывающего

дерева [17]. Этот алгоритм используется для проверки связности

графа и определения

его компонентов. Основная идея алгоритма

заключается в просмотре всех ветвей на предмет включения их в

дерево, покрывающее весь граф. Ветвь включается в покрывающее

дерево, если она не образует контур с ветвями, уже включенными в

покрывающее дерево.

Рассмотрим один из возможных видов этого алгоритма. Каждая

ветвь просматривается только по одному разу. При

этом практически

одновременно формируется несколько разрозненных фрагментов

покрывающего дерева, которые постепенно соединяются между

собой.

Шаг 1

. Узлы, инцидентные первой просматриваемой ветви,

относят к некоторому множеству узлов покрывающего дерева, к

первому фрагменту. Ветвь окрашивается.

Шаг 2.

Анализируется последующая ветвь. При этом возможны

ситуации следующих типов:

140

1) оба конца ветви принадлежат одному и тому же фрагменту,

то есть ветвь образует контур;

2) один конец ветви принадлежит одному из сформированных

ранее фрагментов, а другой не принадлежит ни одному из них. Этот

узел также включается в состав фрагмента, к которому относился

первый конец (узел) ветви, а сама ветвь окрашивается;

концы (узлы) ветви инцидентны различным фрагментам; оба

эти фрагмента объединяются в один, а ветвь окрашивается;

4) ни один из концов ветви не принадлежит ни к одному из

ранее сформированных фрагментов, формируется новый фрагмент,

ветвь окрашивается.

Шаг 2 повторяется многократно. Контроль завершения

процедуры осуществляется на шаге 3.

Шаг 3

. Возможны две ситуации после выполнения очередного

шага:

1) все узлы графа вошли в один фрагмент; тогда окрашенные

ветви образуют покрывающее дерево;

2) все узлы графа вошли в сформированные несколько

фрагментов; система разделилась на независимые части.

Если при разделении системы ее части оказались не

сбалансированными по мощности источников и потребителей и в

них

образовался дефицит, то такое состояние системы является

аварийным.

Алгоритм исследования состояний системы представлен на

рис. 6.9 и включает в себя следующие операции:

- ввод расчетной схемы, схемы управления, графика нагрузки,

показателей надежности ветвей;

- формирование возмущающих воздействий;

- формирование схемы сети после реакции на возмущающее

воздействие, отвечающей очередному рассматриваемому состоянию;

- расчет узловых

нагрузок по пропорциональной модели;