Гук Ю.Б. Теория надежности. Введение: учеб. пособие

Подождите немного. Документ загружается.

151

Из-за случайности выборки возможны ошибки при оценке всей

партии по выборочным характеристикам. Различаются ошибки

первого и второго рода. Ошибка первого рода заключается в том, что

испытуемая годная партия изделий по результатам выборки

оценивается как негодная. Вероятность браковки годной продукции

называют риском поставщика. Ошибка второго рода заключается в

том, что испытуемая негодная партия оценивается по результатам

выборки как годная. Вероятность пропуска бракованной партии

называют риском потребителя.

Для уверенного различения годной и негодной продукции

устанавливаются три категории: хорошая подукция, допустимая

продукция и брак. Например, если средняя наработка по результатам

испытаний выборки

ср

≥ T

, то продукция хорошая. Если t

ср

< T

, то

продукция бракуется. Установленные границы:

– приемочное

число,

– браковочное число и заданные значения рисков α и β

определяют объем испытаний.

В случае однократной выборки ГОСТ 27.410-87 регламентирует

следующие значения

α = β = 0,1; 0,2; 0,3 и отношения T

= D = 1,5;

2,0; 3,0; 5,0. В зависимости от этих величин регламентируются:

предельная сумма учитываемых наработок (в относительных

единицах

= T

) и предельное число отказов r

(табл. 7.1). Если до

достижения предельной суммарной учитываемой наработки не

наступит предельного числа отказов, партия принимается. Если

предельное число отказов наступит до достижения предельной

суммарной учитываемой наработки, то партия бракуется. Предельная

суммарная учитываемая наработка приближенно оценивается по

числу изделий в выборке

N и времени испытаний t

= Nt

). Число

изделий в выборке при отсутствии восстановления при испытаниях

. При условии восстановления в ходе испытаний число изделий

(мест на стенде) может быть и меньше предельного числа отказов.

152

Пример 7.2. Вернемся к результатам примера 7.1. Число отказов

5, число изделий 30. Пусть отказавшие изделия дали следующие

величины наработок до отказа: 120, 150, 180, 210, 240 ч. Тогда

суммарная учтенная наработка составляет

T = 240·(30 – 5) + 120 + 150 + 180 + 210 + 240) = 6900 ч.

Если принять

= 1000, а T

= 500 часов, то D = 2. Значению

D = 2 отвечают вторая, шестая и девятые строки табл. 7.1 (значения α

β = 0,1; 0,2; 0,3 соответственно).

При

α = β = 0,1 Т

= 9,4748; r

= 14; T

= 9474,8 > 6900 и,

следовательно, испытания надо продолжить. Поскольку пока

получено 5 отказов, весьма вероятно, что за оставшиеся 9475 – 6900 =

= 2575 часов число отказов не достигнет 14 и партия может быть

принята.

При

α = β = 0,2 Т

= 3,9311; r

=6; T

= 3931,1 < 6900 и,

следовательно, испытания надо было остановить раньше, не

дожидаясь второго отказа, когда суммарная учтенная наработка стала

равной

T = 150·29 +120 = 4470. Не сложно подсчитать, что после

первого отказа надо было еще продолжать испытания в течение

(4470 – 3931)/29 = 18,4 часов и принять партию.

При

α = β = 0,3 Т

= 1,8543; r

= 3; T

= 1854,3 < 6900 и,

следовательно, партию надо было принять, не дожидаясь первого

отказа после испытаний в течение 1854,3/30 = 61,8 ч.

Вероятность безотказной работы в течение 240 часов при

средней наработке, гарантированной на 90% (

α = β = 0,1), равной

1000 ч, получим как exp(– 240/1000) = 0,7866, что гораздо меньше,

чем заявленная в примере 7.1 величина 0,9. Если принять

= 5000 ч,

то вероятность безотказной работы в течение 240 часов станет равной

exp(– 240/5000) = 0,9531. Но условия испытаний при этом изменятся и

установить их объем можно предоставить читателю для закрепления

знаний этого раздела.

153

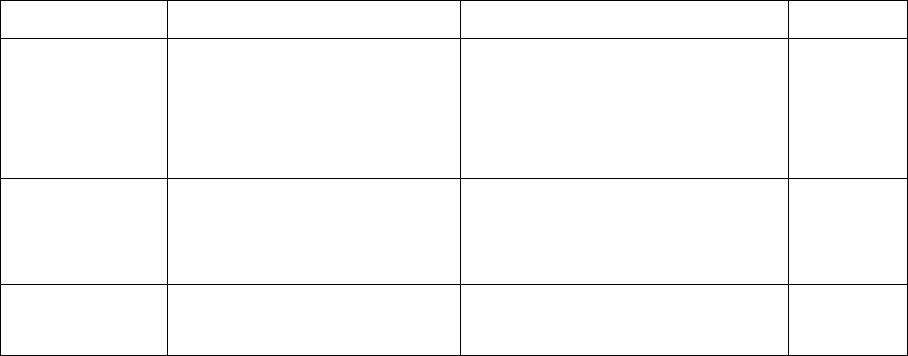
Таблица 7.1

Регламент принятия решения

α = β T

= D T

= T

0,1

1,5

2,0

3,0

5,0

32,1676

9,4748

3,1163

1,0784

0,2

1,5

2,0

3,0

14,3277

3,9311

1,4705

0,3

1,5

2,0

5,4089

1,8543

7.3. Проверка статистических гипотез

Возможности статистического анализа и оценки надежности

определяются объемом наблюдений: числом объектов, временем

наблюдений и количеством регистрируемых событий. Чем больше

объем наблюдений, тем точнее количественные оценки и тем более

сложный качественный анализ может быть выполнен на базе этих

наблюдений. Поэтому существует необходимость объединения

статистических данных, собранных в различных энергосистемах, на

различных установках

. В связи с этим возникает задача проверки

гипотезы об однородности статистического материала объединяемых

наблюдений.

Получив положительный ответ относительно однородности и

объединив массивы данных, можно построить представительные

гистограммы, отражающие эмпирический закон распределения

вероятностей наблюдаемой случайной величины (например,

наработки на отказ). По виду полученной гистограммы может быть

выдвинута гипотеза о законе распределения.

Проверка этой гипотезы,

в случае положительного ответа, дает основание для применения

154

принятого закона при оценках показателей надежности. В случае

отрицательного ответа следует отказаться от использования данного

закона и тем самым избежать систематической ошибки в оценках.

Можно попытаться проверить гипотезу другого закона. В случае

отрицательного результата и в этом случае следует признать, что

закон распределения не известен и использовать соответствующие

методы оценки.

Пусть

помимо выборки x

, x

, ... , x

имеются также взаимно

независимые случайные величины

, x'

, ... , x'

, распределенные

одинаково и непрерывно, но принадлежащие другой выборке.

Объединим и эти совокупности, расположив в порядке возрастания

значений:

, x"

, ... , x"

n+m

Обозначим символом

(x) функцию эмпирического

распределения, соответствующего выборке

, x'

, ... , x'

, и F

(x) –

функцию, соответствующую выборке

, x

, ... , x

. Основная или

нулевая гипотеза

, подлежащая проверке, заключается в

предположении, что обе выборки извлечены из одной и той же

совокупности, а значения функций распределения величин

x и x'

одинаковы. Методы проверки нулевой гипотезы без оценки вида

распределения показателя однородности называются

непараметрическими. Существуют несколько критериев

однородности [13] и соответствующие программы для ЭВМ,

позволяющие принимать или отвергать гипотезу

с заданным

уровнем значимости (доверия).

Самая простая проверка однородности может быть

осуществлена с помощью оценки случайной величины разности

частот событий в объединяемых группах наблюдений

D = w

– w

и ее

дисперсии

() (1 )

Dw w

⎛⎞

σ=− +

⎜⎟

⎝⎠

155

где w

– частота событий в группе 1, w

= m

; w

– частота

событий в группе 2,

= m

; w – средняя частота событий,

;

– суммарная наработка в группе 1; S

– суммарная наработка в

группе 2;

– число событий в группе 1; m

– число событий в группе

Случайная величина

D распределена приблизительно нормально

(чем больше сумма

+ m

, тем ближе к нормальному

распределению), то есть

() 0,5Ф

()

⎛⎞

⎜⎟

⎝⎠

где Ф

– функция Лапласа, значения которой приводятся в

справочниках. Используя эту формулу, можно оценить вероятность

случайного получения значения разности, равного или большего, чем

наблюдаемое при объединении групп 1 и 2,

q = 1 – F(D). Если

величина

q оказывается слишком мала, то это означает, что

полученное значение разности не случайно, и группы не относятся к

одной генеральной совокупности, то есть статистический материал

двух групп не однороден.

Пример 7.3. Объединим две группы наблюдений за дизель-

генераторами с числами отказов 2 и 1 и наработками 45 и 15 лет

(единиц

× лет). Получим среднюю частоту отказов 0,05 и оценку q =

36,6%. На основании этой оценки можно заключить, что объединение

допустимо.

Результаты проверки однородности статистических данных

семи крупных энергосистем показали, что объединение статистики

повреждений линий, трансформаторов и генераторов вполне

обосновано и, следовательно, использование показателей надежности

электрооборудования, полученных на основе объединения данных

156

всех энергосистем страны [7], в расчетах надежности не должно

вызывать сомнений.

Проверка гипотезы о законе распределения случайной величины

производится с помощью критериев согласия. Гипотеза выдвигается

на основании теоретических предположений или моделей и

проверяется путем сравнения теоретической функции распределения

F(t) c эмпирическим распределением, представленным гистограммой

G(t) накопленных частостей для упорядоченного ряда результатов

наблюдений случайной величины:

, t

, ... , t

. На рис. 7.1 показаны

функции

F(t) и G(t) построенные по данным наблюдений,

приведенным в примере 7.4.

Количественная оценка согласия опытного и теоретического

распределения осуществляется с помощью критериев

А. Н. Колмогорова, хи-квадрат и омега-квадрат (ГОСТ 11006-74).

Число наблюдений случайной величины для проверки согласия

распределений должно быть больше 100 при использовании первых

двух критериев и более 50 при использовании последнего.

Рис. 7.1. Теоретическая и эмпирическая функции распределения

(к примеру 7.4)

Погрешность измерения случайной величины не должна

превышать 10% предполагаемого среднеквадратического отклонения.

Последовательность применения критериев: сначала проверка

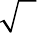
157

осуществляется по критерию Колмогорова. Если гипотеза в

результате проверки отвергается, то дальнейшей проверки не

требуется. Если проверка по критерию Колмогорова не отвергает

гипотезу, то требуется проверка по одному из двух критериев. При

большом числе наблюдений – по критерию хи-квадрат, при малом

числе наблюдений – по критерию омега-квадрат. Для всех критериев

существуют

вычислительные программы, входящие в программное

обеспечение для статистических исследований.

В работе [7] приводятся результаты проверки гипотезы о

пуассоновском характере распределения числа отказов элементов

электроустановок и экспоненциальном характере распределения

наработок на отказ. Проверка выявила явную нестационарность

потока повреждений линий электропередач и сборных шин и

экспоненциальный характер распределения наработок на отказ

электрических машин

и коммутационной аппаратуры.

Остановимся на простейшем критерии согласия – критерии

Колмогорова, который использует для характеристики расхождения

функций максимум разности значений

G(t) и F(t) для n значений

аргумента, зарегистрированных при испытаниях или эксплуатации

= max ⎢G(t) – F(t)⎥.

Колмогоров доказал, что случайная величина

y = D

n имеет

функцию распределения

K(y) = 1 – p(y) (табл. 7.2). Получив в

результате сравнения функций

G(t) и F(t) в n точках значение D

вычислив

y, можно по таблице оценить вероятность p(y) случайного

получения подобного значения

y. Если p(y) > 0,3 ... 0,4, то считают,

что опытная и теоретическая функция хорошо согласуются между

собой, если

p(y) < 0,05...0,10, это означает, что наблюдаемое

отклонение не случайно, то есть теоретическая функция плохо

согласуется с опытными данными.

Критерий согласия Колмогорова предполагает, что вид

распределения известен из каких-либо предпосылок теоретического

158

характера. В случае определения параметров теоретической функции

по данным выборки он дает завышенную оценку согласия.

Пример 7.4. Воспользуемся результатами испытаний из примера

2. Имеется пять значений наработок до отказа

: 120, 150, 180, 210,

240 ч и 25 учтенных наработок по 240 ч. Тогда суммарная учтенная

наработка составляет

T = 240·(30 – 5) + 120 + 150 + 180 + 210 + 240 = 6900 ч.

Средняя наработка на отказ равна

ср

= 6900/5 = 1380 ч. Значения

эмпирической функции распределения вычислим для пяти

зарегистрированных наработок на отказ. Для этих же наработок

вычислим значения теоретической функции распределения, приняв в

качестве гипотезы экспоненциальный закон,

F(t) = 1 – exp(–t/t

ср

), и

абсолютные значения разности теоретической и эмпирической

функций:

G(120) = 1/30 = 0,033;

F(120) = 1 – exp(–120/1380) = 0,083;

D = 0,050;

G(150) = 2/30 = 0,067;

F(150) = 1 – exp(–150/1380) = 0,103;

D = 0,036;

G(180) = 3/30 = 0,100;

F(180) = 1 – exp(–180/1380) = 0,122;

D = 0,022;

G(210) = 4/30 = 0,134;

F(210) = 1 – exp(–210/1380) = 0,141;

D = 0,007;

G(240) = 5/30 = 0,167;

F(240) = 1 – exp(–240/1380) = 0,160;

D = 0,007.

Максимальное значение

= 0,05, при n = 5

y = 0,05 0, 05 = 0,1118.

159

Значение p(y) = 1, следовательно, гипотеза экспоненциального

закона не отвергается. По крайней мере, она подходит для наработок

до 240 часов.

Таблица 7.2

Значения функций р(y)

y p(y) y p(y) y p(y)

0,3 1,0 0,9 0,398 1,5 0,022

0,4 0,997 1,0 0,270 1,6 0,012

0,5 0,964 1,1 0,178 1,7 0,006

0,6 0,864 1,2 0,112 1,8 0,003

0,7 0,711 1,3 0,068 1,9 0,002

0,8 0,544 1,4 0,040 2,0 0,001

Проверка гипотезы о характере распределения

F(x) случайной

величины

X по критерию Пирсона

. На основании каких-либо

теоретических предположений выдвигается гипотеза о законе

распределения

. За меру расхождения статистического и

теоретического законов распределения случайной величины

принимается величина

()

mnp

−

χ=

∑

где

l - число интервалов, на которые разбиты все наблюдения

(значения)

Х;

n – объем выборки;

– количество наблюдений в i-ом интервале;

– вероятность попадания случайной величины X в i-ый

интервал, вычисленная для теоретического закона распределения.

Теоретическое количество значений

X в i-ом интервале – np

Значение

, вычисленное по опытным данным, сравнивается с

160

табличным значением критической точки распределения

(,)

кр kα

χ .

Здесь α – принятый уровень значимости (вероятность допустить

ошибку первого рода) и

k – число степеней свободы, равное

k = l – r – 1,

где

r – количество параметров закона распределения (при

нормальном законе

r = 2, при экспоненциальном r = 1).

Если

(,)

кр kα

χ , то гипотезу отвергают. В противном случае

нет оснований отвергать принятую гипотезу. Рассмотрим алгоритм

проверки

нормального распределения:

• выборку наблюдений объемом n > 50 разбить на несколько (l)

равных интервалов, так чтобы в каждый из интервалов попало не

менее 5 – 8 значений;

• зафиксировать границы каждого интервала (

– левую,

,пр i

– правую);

• определить количество наблюдений

)

, попавших в каждый

интервал;

• вычислить статистическую вероятность попадания в каждый

из интервалов случайной величины

X по формуле

)

;

• вычислить серединные значения наблюдений для каждого

интервала по формуле

i пр i

= ;

• определить математическое ожидание всей выборки

()

Xxp

∑

)

;

• определить дисперсию

() ( )[ ()]DX M X M X=− , где

()

Xxp

∑

)

;