Григорьева А.А., Тащиян Г.О., Григорьева А.П. Автоматизированный мониторинг конкурентоспособности инновационной машиностроительной продукции

Подождите немного. Документ загружается.

средством нечеткого множества, характеризующих его свойств. В [247,

248, 250, 253] рассматриваются косвенные методы для одного эксперта.

В работе Скала Г.Дж. предлагается параметрическое задание идеально-

го и произвольных объектов, на основе которого вводится мера сходст-

ва между объектом и идеалом. В работах Саати Т.Л. используется под-

ход для описания сложных иерархических свойств. Там же и в [246] для

получения значений функции принадлежности решается задача на по-

иск наибольшего собственного значения матрицы попарных сравнений,

в труде Спрингарна Дж.А. используется метод наибольших квадратов,

в [17] осуществляется поиск наиболее близкого по порядку к оценкам

эксперта числового набора в факторном (параметрическом) пространст-

ве минимальной размерности. В [19, 104] производятся прямые методы

для группы экспертов. В [104, 150] степень принадлежности трактуется

как вероятность.

В [93] предлагается метод построения функции принадлежности,

в определенном смысле согласованной с нечетким групповым предпоч-

тением и заданной в интервальной шкале.

В работах Шера А.П. анализируется возможность построения кос-

венных методов для группы экспертов и обсуждается процедура, позво-

ляющая сводить исходную «размытую» функцию, полученную усред-

нением экспертных оценок, к характеристической функции неразмыто-

го, четкого множества. В [2, 5, 87, 229] предлагаются методы построе-

ния терм-множеств лингвистических переменных. В [5, 229] системати-

зированы правила выбора терм-множеств, приведен способ построения

частотных оценок на основании психологического эксперимента и де-

лается попытка построения методики предварительной обработки экс-

периментальной таблицы для выравнивания статистических данных. В

работах Заде предлагается параметрическое определение функций при-

надлежности термов в зависимости от расстояния до эталонов. В боль-

шинстве перечисленных работ функции принадлежности элементов

терм-множеств строятся одновременно на основе так называемого от-

ношения моделирования, получаемого в виде таблицы, строки и табли-

цы которой соответствуют термам и элементам базового множества.

Но основной трудностью, мешающей интенсивному применению

данных методов при решении практических задач, является то, что

функция принадлежности должна быть задана вне самой теории и, сле-

довательно, ее адекватность не может быть проверена непосредственно

средствами теории. В каждом в настоящее время известном методе по-

строения функции принадлежности формулируются свои требования и

обоснования к выбору именно такого построения. Наиболее прост и в то

же время эффективен в применении метод нахождения функции при-

надлежности исходя из попарных сравнений рассматриваемых элемен-

тов, предложенный Т. Л. Саати [233]. При формировании оценок по-

парных сравнений, обычно, эксперта просят отразить ощущения или

опыт следующим образом: а) установить какой из двух предлагаемых

элементов, по его мнению, более важен; б) оценить восприятие интен-

сивности различия в виде ранга важности по определенной ранговой

шкале.

3.5. Модель определения конкурентоспособности наукоемкой про-

дукции на основе метода попарных сравнений

Специфика данной модели позволяет ее использовать на началь-

ных стадиях жизненного цикла изделий (синтез идеи, НИР, ОКР) [47,

71, 74, 75, 128].

Сравнение альтернатив можно производить по отдельным крите-

риям, в качестве которых могут выступать технические характеристики,

по показателю «значимость технического решения» или в целом по про-

дукции. Рассмотрим, как действует наша модель на примере оценки

стреловых самоходных кранов.

Для оценки конкурентоспособности семи видов стреловых само-

ходных кранов используется лингвистическая переменная β-

»конкурентоспособность» c множеством базовых значений

Т={«низкая», «средняя», «высокая»}; базовое множество X= {К

, К

,К

..., К

} , где К

- модель крана. Исследуются отечественные краны, вы-

пускаемые ОАО «Юргинский машиностроительный завод» (ЮМЗ) и их

зарубежные аналоги:

- Grove-RT-5000 (США); К

- KATO-KP-250 (Япония); К

- Locomo-

MS-313-N (Финляндия); К

- Bendini-DELTA16 (Италия); К

- КС-4372Б

(ЮМЗ); К

- КС -4372В (ЮМЗ); К

- КС-4361А (ЮМЗ). Терм «низкая»

характеризуется нечеткой переменной 〈низкая, Х,

〉. Требуется по-

строить функцию принадлежности

нечеткого множества

, описы-

вающего терм «низкая».

Функция принадлежности

определяется по матрице попарных

сравнений М=||m

||, элементы которой m

представляют собой некото-

рые оценки интенсивности принадлежности элементов x

∈

X нечеткому

множеству

по сравнению с элементами х

∈

X. Если предположить,

что значения функции принадлежности

известны для всех элементов

∈

Х, например,

(х )= r

∈

I = { 1, 2, , п}), то попарные сравнения

можно представить матрицей отношений М, где m

= r

. Если отно-

шения точны, то получается соотношение M

⋅

r = n

⋅

r, r = (r

, r

, ...,r

где п - собственное значение матрицы М, по которому можно восстано-

вить вектор r с учетом условия:

∑

В общем случае эмпирический вектор r = (r

, r

, ..., r

) должен

удовлетворять задаче на поиск собственного значения M

⋅

r =

max

, где

max

- наибольшее собственное значение, и задача сводится к поиску

вектора r, который удовлетворяет уравнению M

⋅

max

⋅

r. Так как из-

вестно, что это уравнение имеет единственное решение, то значения ко-

ординат собственного вектора, соответствующего максимальному соб-

ственному значению, деленные на их сумму, будут искомыми степеня-

ми принадлежности.

Для получения матрицы попарных сравнений производится опрос

эксперта относительно того, насколько, по его мнению, величина

(х

)

превышает величину

), т.е. насколько элемент x

, более значим для

понятия, описываемого нечетким множеством

, чем элемент x

Поня-

тия, которыми оперирует эксперт и интерпретация этих понятий значе-

ниями m

приведены в табл.3.1.

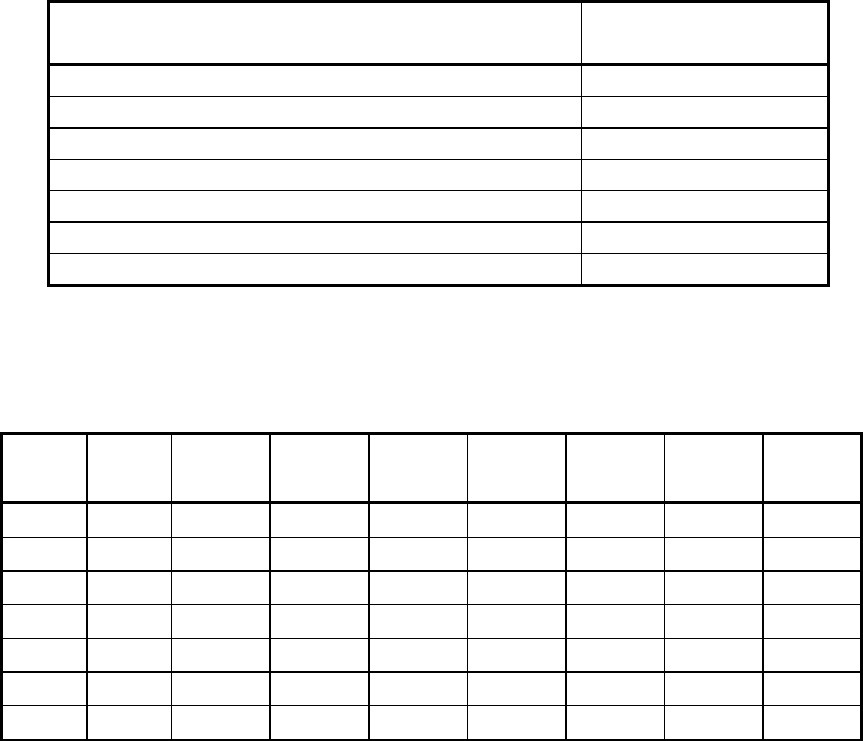
Таблица 3.1

Интерпретация значений m

Смысл m

µ(x

) примерно равна µ(x

)

µ(x

) немного больше µ(x

)

µ(x

) больше µ(x

)

µ(x

) заметно больше µ(x

)

µ(x

) намного больше µ(x

)

Значения, промежуточные по степени между перечисленными

2, 4, 6, 8

Как следует из таблицы, для улучшения согласованности оценок

предполагается, что m

⋅

, откуда m

=1 для диагональных эле-

ментов и т

=1/m

для элементов, симметричных относительно главной

диагонали. Предположим, что экспертный опрос проведен безупречно и

матрица парных сравнений построена абсолютно точно. Тогда матрица

М имеет следующий вид:

. . . r

M = r

. . .r

……………………….

. . . r

В этом случае для определения j-го элемента вектора r (j∈I) мож-

но воспользоваться следующей процедурой. Вычислим сумму элемен-

тов i-го столбца матрицы М. Получим, что эта сумма равна некоторо-

му числу k

,, т.е.

km =

∑

Из построения матрицы получаем, что:

∑∑

jji

rrrm

/1/

Таким образом: r

=1/k

. Продолжая процедуру по всем столбцам

матрицы М, можно построить искомый вектор r.

Для облегчения работы экспертов и получения более точных оце-

нок можно применить многокритериальный подход и оценивать краны

не в целом, а покритериально с помощью показателя «значимость тех-

нического решения».

Краны были оценены следующим образом:

Таблица 3.2

Модель крана

тр

Grove RT-5000 (США) 226,8

КАТО-КР- 250 (Япония) 286,2

Locomo- MS-313N (Финляндия) 84,03

Bendini -DELTA 16 (Италия) 156,9

КС- 4372Б (ЮМЗ) 25,13

КС- 4372В (ЮМЗ) 26,35

КС- 4361А (ЮМЗ) 24,5

На основе этих оценок полученная матрица попарных сравнений

приведена в табл.3.3.

Таблица 3.3

тр

24,5 25,13 26,35 84,03 156,9 226,8 286,2

∑m

24,5 1 1/2 1/3 1/6 1/7 1/8 1/9 2,37

25,13

2 1 1/2 1/3 1/6 1/7 1/8 4,27

26,35

3 2 1 1/2 1/3 1/6 1/7 7,14

84,03

6 3 2 1 1/2 1/3 1/6 13,0

156,9

7 6 3 2 1 1/2 1/3 19,8

226,8

8 7 6 3 2 1 1/2 27,5

286,2

9 8 7 6 3 2 1 36,0

Вычислим значения векторов r

по формуле: 1

∑

=1/2,37=0,43; r

=1/4,27=0,23; r

=1/7,14=0,14; r

=1/13=0,08;

=1/19,83=0,05; r

=1/27,5=0,04; r

=1/36=0,03, т.е.

=(0,43; 0,23; 0,14; 0,08; 0,05; 0,04; 0,03).

Оценим точность экспертного опроса. Для этого последовательно

умножаем вектор r

на каждый столбец матрицы парных сравнений М,

получим вектор r

= M⋅r

= (2,73; 1,79; 1,17; 0,70; 0,41; 0,26; 0,16).

Разделим вектор r

на вектор r

поэлементно, получим вектор:

max

=(6,35; 7,78; 8,36; 8,75; 8,2; 6,5; 5,33),

в котором i – ый элемент (i

∈

I) есть значение ν

max,

соответствующее

элементу r

вектора r. Усредненное значение ν

max

из 7 полученных зна-

чений равно 7, 32. При этом отклонение ν

max

от n может оцениваться

как точность оценивания [115]. Таким образом, отклонение или расчет-

ная точность оценивания составляет:

= (7,32-7)⋅100/7 = 4,6 %

и является удовлетворительной [128].

Нормализуем вектор r

. Нормализация производится вычислением

отношений между степенями принадлежности элементов x

∈

X и вели-

чиной sup

(х). Для этого разделим его каждое значение на 0,43. Иско-

мые степени принадлежности для 7 кранов составят:

= (1; 0,53; 0,33; 0,19; 0,12; 0,1; 0,07).

Аналогично находим функции принадлежности термов «высокая

конкурентоспособность», «средняя конкурентоспособность».

В итоге имеем нечеткое множество

«низкая конкурентоспособ-

ность»:

={(1/24,5), (0,53/25,125), (0,33/26,35), (0,19/84,025), (0,12/156,9),

(0,1/226,8), (0,07/286,2)}. В более наглядной форме это представимо

следующим образом:

={(1/КС-4361А (ЮМЗ)), (0,53/КС-4372В (ЮМЗ)), (0,33/КС- 4372Б

(ЮМЗ)), (0,19/Locomo-MS-313N (Финляндия)), (0,12/Bendini-DELTA16

(Италия)), (0,1/Grove RT-5000 (США)), (0,07/КАТО-КР- 250 (Япония)},

т.е. 1 соответствует крану с наименьшей конкурентоспособностью. На-

хождение функции принадлежности - это первый этап по созданию ма-

тематических моделей на основе теории нечетких множеств.

На основе данного метода был разработан программный комплекс

«Универсал», одной из подпрограмм которого, является «Определение

функции принадлежности». В данный программный продукт входит

усовершенствованная программа «Пороги».

3.6. Описание программы “Универсал”

Основой программы являются математические методы: метод по-

рогов несравнимости и метод попарных сравнений. Причем, данные ме-

тоды можно использовать совместно по каждой из задач. Комплекс пре-

доставляет возможность работы с экспертами в локальной и глобальной

(Internet) сетях. Использование программы “Универсал” многократно

упрощает процесс управления и принятия решений, делая его более эф-

фективным [57].

Требования к компьютеру и программному обеспечению

-тип ЭВМ - IBM PC AT Pentium 150;

-язык - Visual FoxPro 5.0;

-OC - Windows 95;

-объем программы - 300 Кбайт

Функциональное назначение программы «Универсал»

Программа состоит из трех подпрограмм:

- подпрограмма «Связь с экспертами»;

- подпрограмма «Пороги»;

- подпрограмма «Определение функции принадлежности».

Подпрограмма «Связь с экспертами» выполняет следующие

функции:

a) Работа с проектом:

-создание, удаление проектов;

-выбор экспертов для работы с каждым из проектов;

-выбор методов расчета.

b) Работа с экспертами:

-ведение картотеки экспертов;

-ведение рейтинга экспертов;

-указание адреса эксперта в локальной сети или в сети Internet .

Картотека позволяет оценить насколько каждый из экспертов

подходит для решения определенных задач, а также позволяет про-

грамме найти эксперта в сети для передачи ему данных по проекту и

получения от него оценок.

Подпрограмма «Определение функции принадлежности» выпол-

няет следующие функции:

- ввод альтернатив;

- ввод экспертных оценок критериев или альтернатив;

- расчет функции принадлежности;

- создание нечеткого множества.

Область применения программы «Универсал»

Программа «Универсал» является составной частью программно-

го обеспечения системы поддержки принятия решения о конкуренто-

способности наукоемкой продукции и предназначена для сравнения

альтернатив при многокритериальном подходе и в условиях неполноты

и неточности информации.

3.7. Разработка интегральной модели определения

конкурентоспособности продукции

При построении интегральной модели в основе расчета конкурен-

тоспособности продукции используются оценки 4-х групповых показа-

телей или критериев конкурентоспособности: «значимость техническо-

го решения» (Зтр), финансовый приоритет продукции (ФП), эффектив-

ность производства (ЭП) и сбыта продукции (ЭС). Непосредственное

сопоставление показателя качества продукта и показателя его цены по-

зволяет получить весьма ограниченное представление о преимуществах

и недостатках в работе предприятия в области производства и реализа-

ции продукции. Не учитываются факторы, формирующие экономиче-

ские условия производства и сбыта продукции, игнорируется эффектив-

ное управление финансами при решении вопросов о рациональном ин-

вестировании финансовых ресурсов в продукцию. Данная модель уст-

раняет перечисленные недостатки. Применение модели оправдано на

более поздних сроках жизненного цикла изделий (изготовление, реали-

зация, эксплуатация), когда имеется бухгалтерская и статистическая от-

четность [58, 68, 74, 75].

3.7.1. Характеристика групповых показателей оценки конкуренто-

способности продукции

Обзор показателей оценки конкурентоспособности продукции

приведен в табл.3.4. [46]. Имеются широкие возможности для совер-

шенствования данной методики в сторону увеличения количества таб-

лиц для оценки новых характеристик технических решений, расшире-

ния понятий и численных значений в таблицах.

Для обеспечения репрезентативности критерии имеют коэффици-

енты весомости (ранг). Определение ранга критериев является для экс-

перта далеко не простой задача, т.к. при назначении весов он должен

принять во внимание, например, среднестатистические балльные оцен-

ки критериев, диапазон шкалы критерия и т.д.

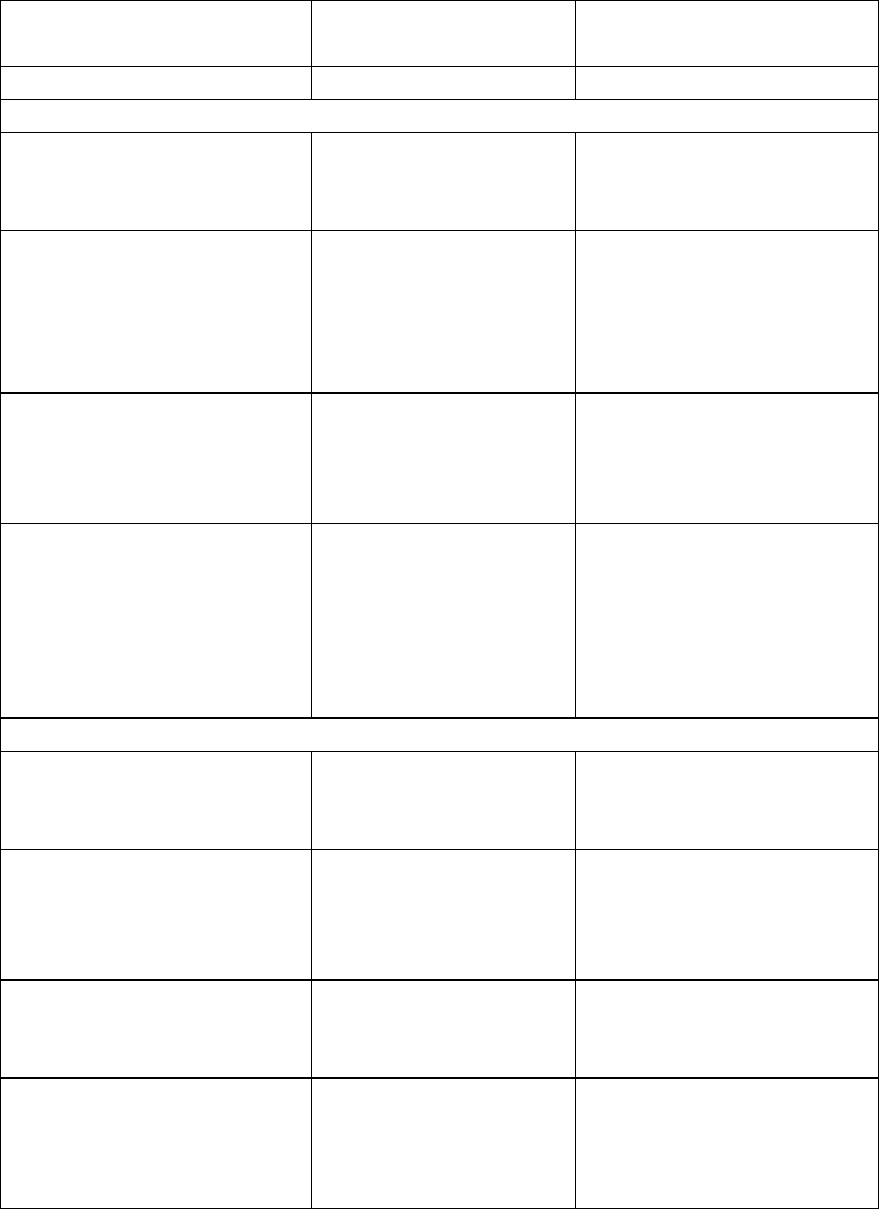
Таблица 3.4

Классификация критериев оценки конкурентоспособности продукции

Критерии и показатели

конкурентоспособности

Роль показателя в

оценке

Правило расчета пока-

зателя

1 2 3

1. Эффективность производства продукции

1.1. Издержки произ-

водства на единицу

продукции

Эффективность за-

трат при выпуске

Валовые издержки /

объем выпуска

1.2.Фондоотдача Эффективность ис-

пользования основ-

ных производст-

венных фондов

(ОПФ)

Объем выпуска

/среднегодовая стои-

мость ОПФ

1.3.

Рентабельность

товара

Степень прибыль-

ности производства

товара

Прибыль от

еалиизации / полная

себестоимость продук-

ции

1.4. Производитель-

ность труда

Эффективность ор-

ганизации произ-

водства и исполь-

зования рабочей

силы

Объем выпуска про-

дукции /ССЧ работни-

ков

2. Критерий финансового приоритета

2.1. Коэффициент авто-

номии

Независимость

предприятия от за-

емных источников

Собственные средства

/ общая сумма источ-

ников финансирования

2.2. Коэффициент пла-

тежеспособности

Способность пред-

приятия выполнять

свои финансовые

обязательства

Собственный капитал /

общие обязательства

2.3. Коэффициент лик-

видности

Способность по-

крывать текущие

обязательства

Денежные средства /

краткосрочные обяза-

тельства

2.4. Коэффициент обо-

рачиваемости

Эффективность ис-

пользования обо-

ротных средств

Выручка от реализа-

ции / среднегодовой

остаток оборотных

средств

продолжение таблицы 3.4

1 2 3

3. Критерий эффективности сбыта

3.1. Рентабельность про-

даж

Степень прибыль-

ности работы на

рынке

Прибыль от реализа-

ции товара / объем

продаж

3.2. Коэффициент зато-

варенности готовой

продукцией

Степень затоварен-

ности

Объем нереализо-

ванной продукции /

объем производства

3.3. Коэффициент за-

грузки производствен-

ной мощности

Деловая активность

предприятия

Объем выпуска /

производственные

мощности

3.4. Коэффициент эф-

фективности рекламы

Эффективность

рекламы

Затраты на рекламу и

стимулирование

сбыта / прирост при-

были от реализации

4. Интегральный пока-

затель «значимость тех-

нического решения»

(Зтр)

Качество продукта,

его технический

уровень

Методические указа-

ния по расчету пока-

зателя Зтр

Результаты исследований показывают существенные различия

между теми весами критериев, которые назначает сам человек, и теми,

которые можно выявить на основе его действий. Обычно завышается

весомость незначительных критериев и недооцениваются наиболее су-

щественные, причем, эти отклонения мало зависят от квалификации

субъекта и характерны как для предпринимателей и экспертов, так и для

менеджеров. Для сглаживания субъективизма при назначении весов был

использован метод попарных сравнений.

Расчет критериев и коэффициента конкурентоспособности прово-

дится по формуле:

=а

⋅

+а

⋅

+а

⋅

+а

⋅

Зт, (3.1)

где К

– коэффициент конкурентоспособности продукции;

– значение критерия эффективности производства продукции;

– значение критерия финансового приоритета от выпуска продук-

ции;

– значение критерия эффективности сбыта продукции;

Зтр– значение интегрального показателя «значимость технического

решения»;

, a

– коэффициенты весомости (степени принадлежности);

= a

⋅

И+а

⋅

Ф+а

⋅

+а

⋅

П , (3.2)

где И– показатель издержек производства на единицу продукции;

Ф– относительный показатель фондоотдачи;

– относительный показатель рентабельности товара;

П– относительный показатель производительности;

,а

– коэффициенты весомости (степени принадлежности);

= а

⋅

лт

⋅

, (3.3)

где k

– коэффициент автономии;

– коэффициент платежеспособности;

лт

– коэффициент текущей ликвидности;

– коэффициент оборачиваемости оборотных средств;

–коэффициенты весомости (степени принадлежности);

⋅

, (3.4)

где P

– относительный показатель рентабельности продаж;

–относительный показатель загрузки производственной мощности;

–относительный показатель эффективности рекламы и стимулирова-

ния сбыта;

– коэффициент затоваренности готовой продукции;

– коэффициенты весомости (степени принадлежности).

Алгоритм включает 3 этапа:

1. Расчет единичных показателей конкурентоспособности

(табл.3.4) и перевод показателей в баллы. Для этого производится их

сравнение с базовыми показателями. В качестве базовых показателей

могут выступать: среднеотраслевые показатели, показатели аналога-

конкурента, показатели за прошлый отрезок времени, показатели лиде-

ра-конкурента на рынке. Главным принципом сравнения является прин-

цип обеспечения сопоставимости результатов на основе принятой шка-

лы экспертных оценок. В целях перевода показателей в относительные

величины (баллы) используется десятичная шкала от 0 до 1. С ее помо-

щью оцениваются параметры продукции с точки зрения их оптимально-

сти для потребителя. Каждому экспертному значению показателя кон-

курентоспособности соответствует конкретная вербальная интерпрета-