Григорьева А.А., Тащиян Г.О., Григорьева А.П. Автоматизированный мониторинг конкурентоспособности инновационной машиностроительной продукции

Подождите немного. Документ загружается.

: «Если он вдобавок к вышеописанным требованиям обладает

интуицией, то он — более чем, удовлетворяющий»;

: «Если он вдобавок к условиям d

имеет способность найти за-

казчика НМП, то он — безупречный»;

: «Если он имеет все, оговоренное в d

, кроме способности обла-

дания интуицией, то он — очень удовлетворяющий»;

. «Если кандидат — очень опытный исследователь, имеет спо-

собность найти заказчика и хороший эксперт, но не имеет произ-

водственного стажа, он все же будет удовлетворяющим»;

: «Если он не имеет квалификации исследователя или не имеет

проверенной способности к экспертизе, он — неудовлетворяющий».

Анализ шести информационных фрагментов дает пять критериев,

используемых в принятии решения: X

— исследовательские способ-

ности; Х

— производственный стаж; X

— опыт работы экспертом; Х

.—

обладание интуицией; Х

— способность найти заказчика.

Будем измерять эти переменные на базовом множестве U кандида-

тов. Обращаясь к шести фрагментам, получаем:

: «Если X

=ОБРАЗОВАННЫЙ и X

=НЕКОТОРЫЙ ОПЫТ и

Хз= =ХОРОШИЙ, то Y =УДОВЛЕТВОРЯЮЩИЙ»;

: «Если X

=ОБРАЗОВАННЫЙ и Х

=НЕКОТОРЫЙ ОПЫТ и

=ХОРОШИЙ и X

=ОБЛАДАЮЩИЙ ИНТУИЦИЕЙ, то Y=БОЛЕЕ,

ЧЕМ УДОВЛЕТВОРЯЮЩИЙ»;

: «Если X

=ОБРАЗОВАННЫЙ и Х

=НЕКОТОРЫЙ ОПЫТ и

=ХОРОШИЙ и X

=ОБЛАДАЮЩИЙ ИНТУИЦИЕЙ и X

СПОСОБ-

НЫЙ, то Y = БЕЗУПРЕЧНЫЙ»;

: «Если X

=ОБРАЗОВАННЫЙ и Х

=НЕКОТОРЫЙ ОПЫТ и Х

=ХОРОШИЙ и X

=ОБЛАДАЮЩИЙ ИНТУИЦИЕЙ, то Y=ОЧЕНЬ

УДОВЛЕТВОРЯЮЩИЙ»;

: «Если X

=ОЧЕНЬ ОБРАЗОВАННЫЙ и X

=НЕ ИМЕЕТ ОПЫ-

ТА и Х

=ХОРОШИЙ и Х

=СПОСОБНЫЙ, то Y = УДОВЛЕТВО-

РЯЮЩИЙ»;

: «Если X

=HEОБРАЗОВАННЫЙ или Х

=НЕ СПОСОБНЫЙ К

ЭКСПЕРТИЗЕ, то Y =НЕУДОВЛЕТВОРЯЮЩИЙ».

Переменная Y задана на множестве J = {0; 0,1; 0,2;...; 1}.

УДОВЛЕТВОРЯЮЩИЙ определено как µ

(x)=x, x∈J,

БОЛЕЕ, ЧЕМ УДОВЛЕТВОРЯЮЩИЙ – как µ

(х)=

, х∈J;

БЕЗУПРЕЧНЫЙ – как µ

(x)=

1 1

0 1

, ;

, ,

если x

≠







ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ – как µ

(x)=x

, х∈J;

НЕУДОВЛЕТВОРЯЮЩИЙ – как µ

(x)=1–x, x∈J.

Выбор производится из пяти кандидатов U={u

, и

, u

Имеются следующие оценки каждого кандидата (см. табл. 2.1):

Таблица 2.1

Исходные данные для выбора кандидата в эксперты

Оценки критериев Аль-

тер-

нати-

вы

Образо-

ванный

исследова-

тель

Произ-

водствен-

ный стаж

Способ-

ность к экс-

пертизе

Интуиция

Способ-

ность

найти за-

казчика

Кан-

дидат

№1

0,8 Образов. 0,5 Средний 0,6 Средняя 1,0 Высокая 0,

Отсуств.

Кан-

дидат

№2

0,6 Вполне 1,0 Большой 0,9 Оч. высок. 0,3 Низкая 0,

Средняя

Кан-

дидат

№3

0,5 Средний 0,0 Отсутств. 1,0 Отличная 1,0 Высокая 1,

Оч.высок.

Кан-

дидат

№4

0,1 Плохой 0,5 Средний 0,7 Высокая 0,0 Отсутсв. 0,

Высокая

Кан-

дидат

№5

0,3 Ниже

среднего

1,0 Большой 1,0 Отличная 0,0 Отсутсв. 0,

Низкая

После этого фрагменты знаний принимают вид

: Если Х=А, и B, и С, то Y=S;

: Если X=A, и B, и С, и D, то Y=MS;

dз: Если X=A, и В, и С, и D, и Е, то Y=Р;

: Если Х=А, и В, и С, и E, то Y= VS;

: Если X= очень A, и не В, и С, и E, то Y=S;

: Если Х=не А или не С, то Y=US.

Используя правило (4.14) для перевода этих операции, получаем

для d

: µ

(u)= min (µ

(u),µ

(u)); M

={0,5/u

; 0,6/u

; 0/u

; 0,1/u

;

0,3/u

};

для d

: µ

(u)= min (µ

(u),µ

(u)); M

={0,5/u

; 0,3/u

;

0/u

; 0/u

};

для d

: µ

(u)= min (µ

(u),µ

(u)); M

={0/u

;

0,3/u

; 0/u

};

для d

: µ

(u)= min (µ

(u),µ

(u)); M

={0/u

; 0,5/u

; 0/u

;

0,1/u

; 0,1/u

};

для d

: µ

(u)= min (µ

(u),1–µ

(u),µ

(u)); M

={0/u

; 0/u

;

0/u

; 0,1/u

; 0/u

};

для d

: µ

(u)= max (1–µ

(u),1–µ

(u)); M

={0,4/u

; 0,4/u

; 0,5/u

;

0,9/u

; 0,7/u

};

Таким образом,

: Если Х=М

, то Y=S;

: Если X=M

, то Y=MS;

: Если X=Mз, то Y=P;

: Если X=M

, то Y=VS;

: Если X=M

, то Y=S;

: Если X=М

, то Y=US.

Используя правило преобразования импликации «Если Х=М, то

Y=Q « в выражении µ

(u, i)= min (1,1–µ

(u)+µ

(u)),для каждой пары

(u,i)∈U

J получаем следующие нечеткие подмножества из U

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

0 5 0 6 0 7 0 8 0 9 1 1 1 1 1 1

0 4 0 5 0 6 0 7 0 8 0 9 1 1 1 1 1

1 1 1 1 1 1 1 1 1 1 1

0 9 1 1 1 1 1 1 1 1 1 1

0 7 0 8 0 9 1 1 1 1 1 1 1 1

, , , , ,

, , , , , ,

, , ,

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

0 5 0 53 0 59 0 66 0 75 0 85 0 96 1 1 1 1

0 7 0 73 0 79 0 86 0 95 1 1 1 1 1 1

1 1 1 1 1 1 1 1 1 1 1

, , , , , , ,

, , , , ,

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

1 1 1 1 1 1 1 1 1 1 1

0 7 0 7 0 7 0 7 0 7 0 7 0 7 0 7 0 7 0 7 1

1 1 1 1 1 1 1 1 1 1 1

, , , , , , , , , ,

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

1 1 1 1 1 1 1 1 1 1 1

0 5 0 51 0 54 0 59 0 66 0 75 0 86 0 99 1 1 1

1 1 1 1 1 1 1 1 1 1 1

0 9 0 91 0 94 0 99 1 1 1 1 1 1 1

, , , , , , , ,

, , , ,

0 0,1 0,2 0,30,40,50,60,70,80,9 1

1 1 1 1 1 1 1 1 1 1 1

0 99 1 1 1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1 1 1 1

0 0,1 0,2 0,3 0,4 0,5 0,6 ,7 0,8 0,9 1

1 1 1 1 1 1 1 0 9 0 8 0 7 0 6

1 1 1 1 1 1 0 9 0 8 0 7 0 6 0 5

1 1 0 9 0 8 0 7 0 6 0 5 0 4 0 3 0 2 0 1

1 1 1 1 0 9 0 8 0 7 0 6 0 5 0 4 0 3

, , , ,

, , , , ,

, , , , , , , , ,

, , , , , , ,

В результате получаем общее функциональное решение:

D=D

∩D

, т.е. µ

(и,i) = min (µ

D j

(u ,i)) ; j=1,...,6

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1

0 5 0 53 0 59 0 66 0 75 0 85 0 96 0 9 0 8 0 7 0 6

0 4 0 5 0 54 0 59 0 66 0 7 0 7 0 7 0 7 0 7 0 6

1 1 1 1 1 1 0 9 0 8 0 7 0 6 0 5

0 9 0 91 0 9 0 8 0 7 0 6 0 5 0 4 0 3 0 2 0 1

0 7 0 8 0 9 0 99 0 9 0 8 0 7 0 6 0 5 0 4 0 3

, , , , , , , , , , ,

, , , , ,

, , , , , , , , , , ,

Для вычисления удовлетворительности каждой из альтернатив

применим правило композиционного вывода в нечеткой среде:

°D , где E

— степень удовлетворения альтернативы k; G

—

изображение альтернативы k в виде нечеткого подмножества U; D —

функциональное решение. Тогда µ

E k

(

)

max min( ( ), ( , ))

u U

Gk Dk

u u i

∈

µ µ

. Кро-

ме того, в этом случае µ

G k

(u)=0, и

≠

; µ

G k

(u)=1, u=u

. Отсюда µ

(i)=µ

, i). Другими словами, E

есть k-я строка в матрице D.

Теперь применим процедуру для сравнения нечетких подмно-

жеств E

, Е

, E

в единичном интервале для получения наилуч-

шего решения.

Для первой альтернативы

= {0,5/0; 0,53/0,1; 0,59/0,2; 0,66/0,3; 0,75/0,4; 0,85/0,5; 0,96/0,6;

0,9/0,7; 0,8/0,8; 0,7/0,9; 0,6/1}.

Вычисляем уровневые множества E

jα .

Их мощность М(Е

jα

) нахо-

дится по формуле

M(E

jα

∑

≤

0,5; d

=0,5;

= {0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; M(E

)=0,5;

0,5<α

≤

0,53; d

=0,03;

= {0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; M(E

)=0,55;

0,53<α

≤

0,59; d

=0,06;

={0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; M(E

) =0,6;

0,59<α

≤

0,6; d

=0,01;

={0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; М(Е

) =0,65;

0,6<α

≤

0,66; d

=0,06;

={0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9}; М(Е

)=0,6;

0,66<α

≤

0,7; d

=0,04;

={0,4; 0,5; 0,6; 0,7; 0,8; 0,9}; М(Е

)=0,65;

0,7<α

≤

0,75; d

=0,05;

={0,4; .0,5; 0,6; 0,7; 0,8}; М(Е

)=0,6;

0,75<α

≤

0,8; d

=0,05;

={0,5; 0,6; 0,7; 0,8}; М(Е

)=0,65;

0,8<α

≤

0,85; d

=0,05;

={0,5; 0,6; 0,7}; М(Е

1α

)=0,6;

0,85<α

≤

0,9; d

=0,05;

={0,6; 0,7}; M(E

1α

)=0,65;

0,9<α

≤

0,96; d

=0,06.

Найдем точечную оценку E

F(E

1 1

0 96

1 1

0 96

α α

max

( )

max

⋅ = ⋅

∫∫

M E d M E d

= 1/0,96×

×(0,5⋅0,5+0,55⋅0,03+0,6⋅0,06+0,65⋅0,01+0,6⋅0,06+ 0,65⋅0,04 + 0,6⋅0,05 +

0,6× ×0,05+ 0,65⋅0,05 + 0,65⋅0,05 + 0,6⋅0,06) = 0,554.

Для второй альтернативы

= {0,4/0; 0,5/0,1; 0,54/0,2; 0,59/0,3; 0,66/0,4; 0,7/0,5;

0,7/0,6; 0,7/0,7; 0,7/0,8; 0,7/0,9; 0,6/1}.

Уровневые множества:

0< α ≤ 0,4; d

=0,4;

= {0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; М(Е

2α

)=0,5;

0,4< α ≤ 0,5; d

=0,1;

={0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; М(Е

2α

)=0,55;

0,5< α ≤ 0,54; d

=0,04;

={0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; М(Е

2α

)=0,6;

0,54< α ≤ 0,59; d

=0,05;

= {0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; М(Е

2α

)=0,65;

0,59< α ≤ 0,6; d

=0,01;

= {0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; М(Е

2α

)=0,7;

0,6< α ≤ 0,66; d

=0,06;

={0,4; 0,5; 0,7; 0,8; 0,9}; М(Е

2α

)=0,65;

0,66< α ≤ 0,7; d

=0,04;

={0,5; 0,6; 0,7; 0,8; 0,9; 1}; М(Е

2α

)=0,75.

Точечная оценка:

F(E

)=1/0,7⋅(0,5⋅0,4+0,55⋅0,1+0,6⋅0,04+0,65⋅0,05+0,7⋅0,01+0,65⋅0,06+0,75⋅

⋅0,04) = 0,554.

Для третьей альтернативы

={1/0; 1/0,1; 1/0,2; 1/0,3; 1/0,4; 1/0,5; 0,9/0,6; 0,8/0,7; 0,7/0,8; 0,6/0,9;

0,5/1};

F(E

)= 1/1⋅ (0,5⋅0,5+0,45⋅0,1 +0,4⋅0,1+0,35⋅0,1+0,3⋅0,1+0,25⋅0,1)=0,425.

Для четвертой альтернативы

={0,9/0; 0,91:/0,1; 0,9/0,2; 0,8/0,3; 0,7/0,4; 0,6/0,5; 0,5/0,6; 0,4/0,7;

0,3/0,8; 0,2/0,9; 0,1/1};

F(E

) = 1/0,91⋅ (0,5+0,45+0,4+0,35+0,3+0,25+0,2+0,15+0,1)⋅0,1+0,1⋅0,01=

= 0,298.

Для пятой альтернативы

= {0,7/0; 0,8/0,1; 0,9/0,2; 0,99/0,3; 0,9/0,4; 0,8/0,5; 0,7/0,6; 0,6/0,7;

0,5/0,8; 0,4/0,9; 0,3/1};

F (E

)= 1/0,99⋅ (0,5⋅0,3+(0,45+0,4+0,35+0,3⋅3)⋅0,1 + 0,3⋅0,09)=0,391.

Таким образом, точечная оценка удовлетворительности для аль-

тернативы u

равна 0,553, и

– 0,554, u

– 0,425, u

– 0,298, u

– 0,391. В

качестве наилучшей выбираем альтернативу u

Т.е. ЛПР наибольшее

предпочтение отдали кандидату с высоким опытом производственного

стажа (степень предпочтения 1) и хорошей способностью к экспертизе

(степень предпочтения 0,9); при этом исследовательские способности и

обладание интуицией как критерии получили меньшие степени пред-

почтения (0,6 и 0,3 соответственно). Это можно объяснить тем, что ис-

следовательские способности приобретаются при проведении теорети-

ческой работы, а уровень интуиции можно получить по мере роста про-

изводственного стажа. Рассмотренный метод принятия решений с ис-

пользованием правил нечеткого вывода является адаптацией нечеткой

логики к процессам принятия решений с исходными данными в виде

точечных оценок.

2.4. Описание программы «Эксперт-Менеджер»

Данная программа создана на основе метода многокритериально-

го выбора альтернатив с учетом разработанных продукционных правил

по выбору экспертов в экспертную группу.

Программа представляет собой 32-разрядное приложение (таким

образом, программа не будет работать на компьютерах с процессором,

класс которого ниже Pentium) для операционной системы Windows 95 и

выше. В процессе работы программа создает файлы баз данных с рас-

ширением DBF, идентичные по формату структуры файлам DBASE IV,

что позволяет использовать базу данных программы к другим приложе-

ниям ввиду распространенности данного формата базы данных (напри-

мер, с программами графического отображения данных, при построении

диаграмм, гистограмм или программ-экспортеров данных). Это увели-

чивает возможности интеграции программы с другими программными

комплексами и решениями.

Также в программе предусмотрен разделенный доступ к базе дан-

ных, что позволяет работать с программой и базой данных одновремен-

но нескольким пользователям. Так, например, база данных может быть

расположена на сервере сети, а на пользователи могут работать со своих

терминалов. Данный способ работы позволяет обеспечивать более бы-

стрый ввод альтернатив, а также возможность каждой альтернативы

экспертом по критериям, являющимися его областью. Однако, проведе-

ние расчета возможно только в, так называемом, «монопольном режи-

ме», когда с базой данных работает только один пользователь.

Программа позволяет сохранять введенные данные, открывать их

в последующем, изменять и удалять, в случае надобности, а так же про-

изводить повторный расчет. Если в прошлом сеансе работы программы

был произведен расчет, то при открытии проекта в следующий раз пе-

рерасчет не требуется, а данные расчета будут открыты вместе с дан-

ными самого проекта.

Программа «Эксперт-Менеджер» использует стандартные диало-

говые средства операционной системы, поэтому если пользователь уме-

ет работать с приложениями операционной системы, то дополнительное

обучение работе с программой ему не требуется, что увеличивает дос-

тупность программного продукта широкому кругу пользователей.

Программа позволяет производить оценку альтернатив по 30 про-

извольным критериям. Каждый критерий может иметь до 11 возможных

значений (как показывает практика, это количество является оптималь-

ным, а в большинстве случаев и избыточным). Допускается произволь-

ное количество продукционных правил оценки альтернатив, с указани-

ем для каждого правила его весомости при расчете общего функцио-

нального решения. В каждом правиле допускается использовать до 5

критериев оценки, по 2 значения на каждый критерий разделенных ло-

гическим оператором «ИЛИ», с возможным вариативным разделением

критериев оператором «И» или «ИЛИ». Во избежание ввода некоррект-

ных значений, в необходимых местах предусмотрен выбор значений из

списка вместо ручного ввода с клавиатуры, что увеличивает надежность

работы программы.

2.4.1 Функциональное назначение программы

Программа «Эксперт-Менеджер» выполняет следующие функции:

ввод альтернатив; ввод критериев; ввод возможных значений критериев;

ввод продукционных правил оценки альтернатив; ввод весов продукци-

онных правил; ввод возможных результатов оценки альтернатив; расчет

степеней соответствия альтернатив каждому продукционному правилу;

построение общего функционального решения; расчет точечных оценок

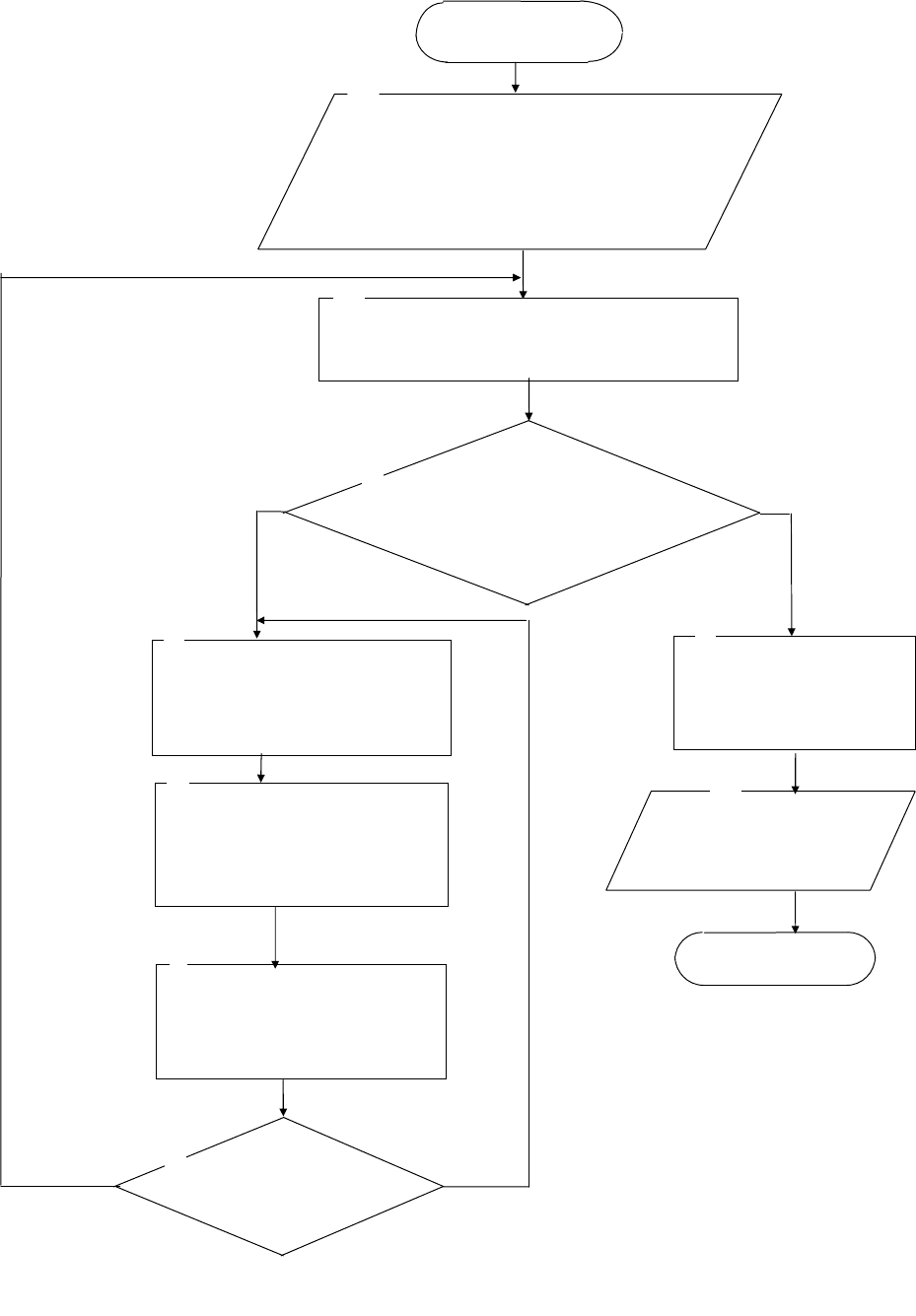
каждой альтернативы. Блок схема алгоритма построения общего функ-

ционального решения и вычисления точечных оценок альтернатив про-

граммы «Эксперт-Менеджер» представлена на рис. 2.1.

2.4.2. Технические требования программы

Минимальные требования к аппаратному обеспечению - IBM PC

AT Pentium 100 (возможны аппаратные решения на базе процессоров не

ниже AMD K6 133). Объем ОЗУ не ниже 16 Мбайт. Операционная сис-

тема - Windows 95 и выше. Объем программы вместе с файлами про-

граммных библиотек - 10,5 Мбайт. Объем необходимого свободного

дискового пространства – не менее 20 Мбайт (при больших проектах

может потребоваться дополнительное дисковое пространство). Видео-

адаптер SVGA. Видеорежим 800х600, манипулятор «мышь».

2.5. Метод Дельфы

Рассмотрим работу группы экспертов в определении конкуренто-

способности продукции методом Дельфы.

В целом, значительные усилия, затраченные при комплектовании

группы, полностью оправданы за счет оптимизации степени точности и

достоверности результатов при минимизации затрат времени и средств.

Начало

Ввод критериев, альтернатив,

результатов и продукционных

правил

Построение об-

щего функци-

онального решения

Вывод точечных

оценок

Сканирование списка

продукционных правил

Построение матрицы

правила

Сканирование

списка альтернатив

Конец списка

правил

да

нет

Расчет оценок соот-

ветствия альтерна-

тивы правилу

Конец списка

альтернатив

да

нет

Рис. 2.1. Блок схема алгоритма расчета точечных оценок

Конец

Разработка эффективного регламента диалога об альтернативах по

выбранным критериям и показателям должна основываться на оценке

влияния на точность результатов содержания информации, которой об-

мениваются эксперты. Можно выделить регламенты с личными контак-

тами между субъектами [85, 151] и многотуровые регламенты без лич-

ных контактов с контролируемой обратной связью.

Каждый из регламентов может быть реализован в АМК НП, одна-

ко, предпочтение по ряду объективных причин отдается второму виду,

наиболее известным из которых является метод Дельфи [125]. Данный

метод имеет множество модификаций, обусловленных конкретной об-

ластью его приложения или связанных с основами организации работы

коллектива экспертов. Можно отметить следующие модификации мето-

да Дельфи: методика итических проблем Policy Delphi, прогнозирование

производства стали, «упрощенный Дельфи», метод Форда, процедура

анализа текстов, процедура с «качественной обратной связью», проце-

дура с «индивидуальной обратной связью» и другие модификации.

Анализ способов организации обратной связи, видов передавае-

мой по ней информации, правил остановки процедур, учет достоинств и

недостатков модификаций метода Дельфи позволил разработать регла-

мент диалога, удовлетворяющий задачам АМК НП. Каждый тур опроса

в соответствии с разработанным регламентом предполагает выполнение

субъектами определенных операций. Однако еще до первого тура опро-

са проводится комплекс подготовительных мероприятий: отбор экспер-

тов и ознакомление их с методикой исследования, разработка форм

электронных таблиц для полного множества критериев и альтернатив,

тестирование готовности технических средств и программного обеспе-

чения АМК НП.

Первый тур опроса предполагает заполнение экспертами таблиц с

неограниченным количеством строк и столбцов. Это позволяет расши-

рить первоначально заданный перечень критериев и оцениваемых объ-

ектов. Таким образом, таблица первого тура не ограничивает экспертов

в масштабе исследования проблемы, и значительно снижает вероят-

ность того, что не будут учтены важные факторы, которые отсутствова-

ли в базовом варианте таблицы. После того как все эксперты предложи-

ли свои варианты таблиц, руководитель исследования принимает реше-

ние об окончательном варианте, который будет использоваться на сле-

дующих этапах. При этом руководитель ориентируется на указанные в

инструкции АМК НП ограничения. Основной принцип – включение в

итоговую таблицу данных, указанных большинством экспертов и ис-

ключение редких второстепенных элементов. Структура таблиц в этом

случае остается прежней, но ограниченной по вертикали и горизонтали.