Грицюк С.Н., Мирзоева Е.В., Лысенко В.В. Математические методы и модели в экономике

Подождите немного. Документ загружается.

20

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Имеем:

Новый критический путь:

На третьем этапе рассматриваем на последнем пути

наличие резерва времени у работы а

. Свободный

резерв времени у работы а

равен:

Снимаем средства х

и записываем условие допус-

тимости . Переносим резервы х

�

некритической

работы а

�

на работы а

, а

�

, а

остальных критических

путей в размерах соответственно и состав-

ляем систему уравнений

Решая эту систему при числовых данных: с

= 0,2;

= 0,9; с

= 1,1; с

= 0,7; t

�

= 6;

; Т

= 37,

получим:

Ограничение выполнено.

(6.40)

21

Математические методы и модели в экономике

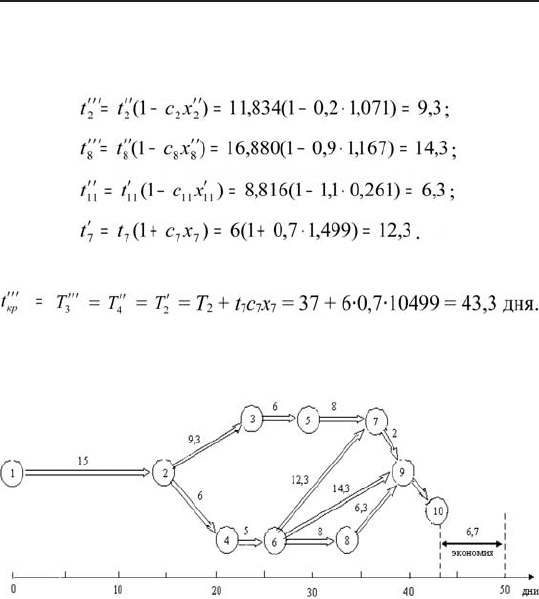
Новое время выполнения работ а

, а

вычис-

ляется по формулам:

Новый критический путь:

Экономия 50 – 43,3 = 6,7 дня.

Построим оптимальный план работ (рис. 6.12).

Рис.6.12. Оптимальный календарный план

Вопросы по теме

Что называется сетевым графиком проекта?

Каковы основные элементы сетевого графика?

Каковы порядок и правила построения сетевых

графиков?

Какой путь в сетевом графике называется крити-

ческим и почему?

Какие бывают и как определяются резервы време-

ни событий и работ в сетевом графике?

Что определяет коэффициент напряженности ра-

боты?

22

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

ГЛАВА 7

МАТЕМАТИЧЕСКИЕ МЕТОДЫ

ПРИНяТИя хОзяйСТВЕННЫх

РЕшЕНИй В УСЛОВИях

НЕОПРЕДЕЛЕННОСТИ

7.1. Виды неопределенности

В предшествующих разделах рассматривались де-

терминированные экономико-математические моде-

ли, то есть модели, в которых не учитывалось влия-

ние неопределенных факторов. Вместе с тем имеется

большое количество экономических задач, в которых

невозможно однозначно определить основные пара-

метры и переменные модели изучаемого процесса или

явления. В этом случае говорят, что принятие хозяйс-

твенных решений осуществляется в условиях неопре-

деленности.

Различают два вида неопределенности. Первый —

это стохастическая неопределенность, или неоп-

ределенность первого порядка, то есть ситуация,

в которой предполагается, что для неопределенных

параметров может быть установлено вероятностное

распределение. В этом случае часто прибегают к изу-

чению функции плотности вероятностей, определяют

среднее значение случайной величины, ее дисперсию

и т. п., что в конечном счете позволяет сделать вы-

вод о допустимом варианте хозяйственного решения

по некоторому заранее определенному, как правило,

пороговому критерию. Применение вероятностных

методов моделирования экономических процессов

оправдывает себя только в тех случаях, когда есть

возможность накопить и обработать большое коли-

чество статистической информации, обеспечивающей

репрезентативность анализируемых выборок.

2

Математические методы и модели в экономике

Второй вид неопределенности — это неопределен-

ность, при которой неизвестно вероятностное рас-

пределение интересующей величины, но определена

область ее изменения. Неопределенность такого вида

называют неопределенностью второго порядка.

Возникает неопределенность второго порядка по двум

причинам: в связи с действием людей, преследующих

иные цели в некоторой экономической ситуации, или

в связи с поведением некоторых непредсказуемых

природных факторов.

Для принятия подобных решений предлагаются не-

которые логические критерии принятия хозяйствен-

ных решений.

Одним из таких подходов является принцип га-

рантированного результата. Его смысл состоит

в том, что выбирается такой х-параметр (план или

управление), определяемый нами, при котором не-

который интересующий нас показатель W(x,у) до-

стигает наилучшего (наибольшего) значения при

условии, что у, неопределенный параметр, прини-

мает наихудшее значение. Математически принцип

гарантированного результата определяется по сле-

дующему алгоритму.

1. Для каждого управления х находится наихудшее

значение показателя W(x,y):

2. После этого выбирается такое управление х  X,

при котором достигается наибольшее значение Wm (х):

Величина W* — это такое значение показателя

W(x, у), которое мы можем гарантировать при на-

ихудшем для нас поведении (значении) неопределен-

ного параметра y. Этот критерий выбора называется

критерием Вальда.

(7.1)

(7.2)

2

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Противоположный принципу гарантированного ре-

зультата подход основан на оптимистическом пред-

положении, что неизвестный параметр у будет при-

нимать наилучшие для нас значения. В этом случае

выбор управляющего решения основывается на опре-

делении W* по формуле

Однако этот критерий слишком оптимистичен, по-

этому чаще применяется критерий Гурвица, состоя-

щий в выборе такого управления х, при котором до-

стигается

где α принимает значение от 0 до 1. При α = 1 по-

лучается пессимистический подход к принятию реше-

ния на основе принципа гарантированного результата,

при α = 0 — оптимистический подход. Объективных

основ для выбора коэффициента а не существует.

Интересен подход, предложенный Л. Сэвиджем.

Он состоит в следующем. Для каждого значения у  Y

находится функция:

которая показывает, какое наилучшее значение по-

казателя W(x,y) можно получить при каждом значе-

нии у  Y.

Это значение показателя можно было бы получить,

если бы было известно значение параметра у заранее.

Строится новый показатель:

Показатель называется функцией риска (функцией

потерь или функцией сожалений). Он показывает по-

(7.3)

(7.4)

(7.5)

(7.6)

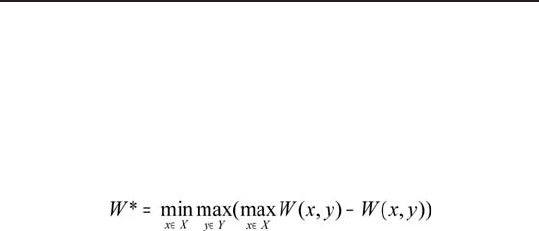
2

Математические методы и модели в экономике

тери (отклонения от наилучшего значения В(у)) для

каждого управления х  X при всех значениях пара-

метра у  Y. Критерий Сэвиджа состоит в выборе реше-

ния на основе функции риска V(x, у) с использованием

принципа гарантированного результата, то есть ищется

такое решение, при котором достигается:

Использование этого подхода позволяет уменьшить

риск при принятии решения.

Тем не менее необходимо помнить, что все приве-

денные критерии имеют высокую степень произволь-

ности.

7.2. Модели систем массового

обслуживания

Характерным примером стохастических задач яв-

ляются модели систем массового обслуживания.

Системы массового обслуживания имеют повсемес-

тное распространение. Это телефонные сети, желез-

нодорожные и авиационные кассы, автозаправочные

станции и т. п. Основным признаком систем массо-

вого обслуживания является наличие некоторой об-

служивающей системы, которая предназначена для

осуществления действий согласно требованиям посту-

пающих в систему заявок . Заявки поступают в сис-

тему случайным образом. Поскольку обслуживающая

система, как правило, имеет ограниченную пропус-

кную способность, а заявки поступают нерегулярно,

то периодически создается очередь заявок в ожида-

нии обслуживания, а иногда обслуживающая систе-

ма простаивает в ожидании заявок. И то, и другое

в экономических системах влечет непроизводитель-

ные издержки (потери), поэтому при проектирова-

нии систем массового обслуживания возникает задача

(7.7)

2

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

нахождения рациональной пропускной способности

системы, при которой достигается приемлемый ком-

промисс между издержками от простоя в очередях в

ожидании выполнения заявки и простоя системы от

недогрузки. Впервые задачи такого типа были реше-

ны в работах А. К. Эрланга в начале прошлого века

и легли в основу «Теории массового обслуживания»,

которая успешно развивается в настоящее время.

Таким образом, система массового обслуживания

состоит из блока обслуживания, потока заявок и

очереди в ожидании обслуживания.

Блоки обслуживания в различных системах разли-

чаются между собой по многим показателям. Во-пер-

вых, блок обслуживания может состоять из одного или

нескольких «приборов». Под прибором понимается ус-

тройство или человек, обслуживающий заявки. Напри-

мер, в магазине может быть одна или несколько касс.

В первом случае система называется одноканальной,

во втором — многоканальной. Во-вторых, системы

массового обслуживания могут быть однофазными и

многофазными. В первом случае заявка обслужива-

ется только одним прибором, во втором — последова-

тельностью приборов. Например, касса в магазине —

однофазная система, сберкасса — двухфазная, пос-

кольку сначала клиент обслуживается контролером, а

только затем получает деньги у кассира.

Вторая составляющая систем массового обслужива-

ния — входной поток заявок. Обычно предполагают,

что входной поток подчиняется некоторому вероят-

ностному закону для длительности интервалов между

двумя последовательно поступающими заявками, при-

чем закон распределения считается не изменяющимся

в течение некоторого достаточно продолжительного

времени. Источник заявок неограничен.

Третья составляющая — дисциплина очереди. Эта

характеристика описывает порядок обслуживания за-

явок, поступающих на вход системы. Чаще всего при-

меняется дисциплина: «первым пришел — первым

2

Математические методы и модели в экономике

обслужен». Но возможны и другие порядки обслужи-

вания: «первым пришел — последним обслужен»,

случайный порядок обслуживания, обслуживание с

приоритетами.

В качестве примера применения системы массового

обслуживания рассмотрим задачу проектирования ав-

тозаправочной станции (АЗС).

Пусть необходимо выбрать один из нескольких ва-

риантов строительства АЗС. Автомобили прибывают

на станцию случайным образом и, если не могут быть

обслужены сразу, становятся в очередь. Дисциплина

очереди — «первым пришел — первым обслужен».

Предположим для простоты, что во всех вариантах

рассматривается только одна бензоколонка, а вариант

от варианта отличается лишь ее мощностью.

Предположим, статистические наблюдения позво-

лили получить величину среднего количества клиен-

тов µ, обслуживаемых в единицу времени. Обратная

величина 1/µ определяет среднее время обслуживания

одного клиента.

Далее допускается стандартное предположение,

что вероятность того, что обслуживание одного кли-

ента, находящегося в процессе обслуживания в мо-

мент t , будет завершено в малом промежутке вре-

мени [t, t + τ], приблизительно равна µτ, где µ > 0.

Вероятность того, что обслуживание не закончится,

считается приблизительно равной 1-µτ , а вероят-

ность того, что будет закончено обслуживание двух

или более клиентов, — пренебрежимо малой величи-

ной. Тогда плотность распределения времени обслу-

живания имеет экспоненциальное распределение:

Далее, исходя из того, что клиенты прибывают на

АЗС случайно, предполагается, что вероятность при-

бытия одного клиента за любой малый промежуток

времени [t, t + τ], начинающийся в произвольный

(7.8)

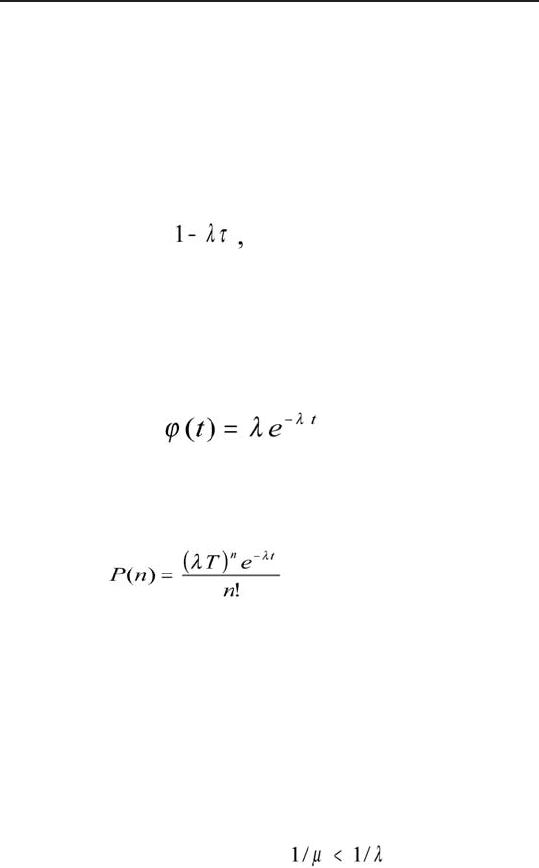
2

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

момент времени t и имеющий длину τ, с точностью до

пренебрежимо малых величин пропорциональна τ с не-

которым коэффициентом пропорциональности λ > 0. Ве-

личина λ интерпретируется как среднее число клиентов,

появляющихся в АЗС за единицу времени, а обратная

ей величина 1/λ — как среднее время появления одного

клиента. Вероятность того, что за этот промежуток вре-

мени не прибудет ни одного клиента, считается прибли-

зительно равной а вероятность прибытия двух

или более клиентов — пренебрежимо малой величиной

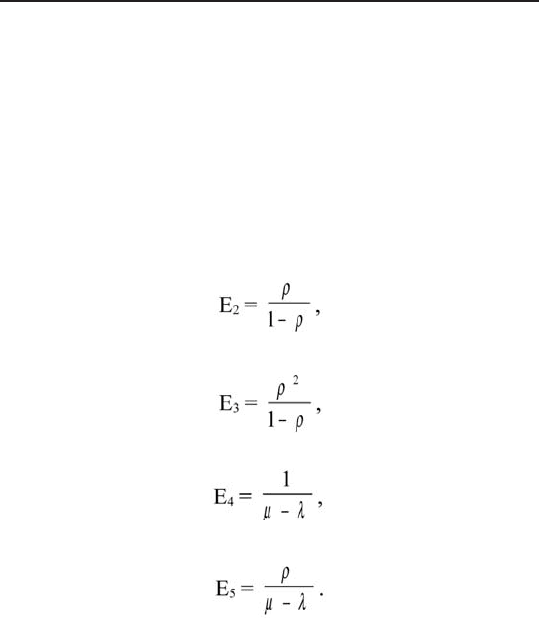
по сравнению со значением λτ. Из выдвинутых пред-

положений в теории вероятностей делаются следующие

выводы. Во-первых, промежутки времени τ между двумя

последовательными появлениями клиентов удовлетво-

ряют экспоненциальному распределению:

, t ≥ 0.

Во-вторых, вероятность того, что за любой уже не

малый период времени � прибудет п клиентов, под-

считывается по формуле

, n = 0, 1, 2, ...

то есть входной поток заявок является пуассонов-

ским.

Отметим, что, в отличие от среднего количества ав-

томобилей, прибывающих в единицу времени на АЗС,

то есть величины λ, величина µ зависит от выбранно-

го нами варианта строительства АЗС. Поэтому имеет

смысл рассматривать те проекты АЗС, для которых

среднее время обслуживания 1/µ меньше среднего

промежутка времени 1/λ между прибытием клиентов,

ибо в противном случае очередь будет постоянно рас-

ти. В том же случае, когда , через некото-

рое время после начала работы система перейдет в

стационарный режим, то есть ее показатели не будут

зависеть от времени.

(7.9)

(7.10)

2

Математические методы и модели в экономике

Обозначив отношение λ/µ через ρ, можно показать,

что стационарный режим устанавливается при ρ < 1.

Величину ρ называют нагрузкой системы. Тогда ос-

новные характеристики системы массового обслужи-

вания определяются по формулам:

•

коэффициент простоя системы

= 1 – ρ,

•

среднее число клиентов в системе

•

средняя длина очереди

•

среднее время пребывания клиента в системе

•

время пребывания клиента в очереди

На основе анализа значений приведенной системы

показателей, характеризующих систему массового об-

служивания, делается вывод о целесообразности вы-

бора варианта строительства АЗС.

Пример

Пусть для общих условий постановки задачи по

проектированию АЗС известны следующие данные:

средний интервал между прибытиями автомобилей

составляет 4 минуты. Варианты строительства АЗС

имеют следующие средние времена обслуживания ав-

томобилей: 5 мин, 3,5 мин, 2 мин, 1 мин, 0,5 мин.

Результаты расчетов по исследованию различных ва-

риантов строительства АЗС сведены в табл. 7.1.

(7.11)

(7.12)

(7.13)

(7.14)

(7.15)