Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


490 7. Nonperturbative QCD
7.2 QCD Sum Rules
In this section we discuss the techniques of QCD sum rules, which allow an
approximate phenomenological treatment of nonperturbative effects in QCD. It
turns out that this method is extremely useful in calculating the lowest-mass
hadronic bound states or determining effective coupling constants. In addition,
QCD sum rules offer some surprising insights into the internal wave functions
of nucleons and pions.
The basic ideas of QCD sum rules are met frequently in QCD. As the full
QCD interaction is strongly nonperturbative and can be solved exactly only in
special cases (e.g., using lattice gauge theories; see Sect. 7.1), one attempts to
separate perturbative and nonperturbative contributions, describing the latter by
a set of phenomenologically effective Feyman rules.
The starting point for QCD sum rules, first formulated by M.A. Shifmann,
A.I. Vainshtein, and V.I. Zakharow in 1979,
16
is the operator product expansion
we met in Sect. 5.4. The OPE gives a general form for the quantities of interest,
and QCD sum rules are a phenomenological procedure for evaluating the ma-
trix elements of the operators that occur. This is a general procedure with many
applications. We shall introduce it by discussing a specific application: the deter-
mination of hadron masses. For this purpose the operator to be expanded is the
general time-ordered product of two currents:
i
dx e
iq·x
T [j
Γ
(x) j
Γ
(0)]=C
Γ
i
+
n
C
Γ
n
(q)O
n
. (7.201)
The operators O
n
can be ordered by their naive dimension (dim[q]=3/2,
dim[G
µν
]=2, dim[m]=1). As we shall be interested only in vacuum expec-
tation values, we can restrict ourselves to spin-0 operators, which are
, d = 0 ,
O
m
=m
¯
qq , d = 4 ,
O
G
= G
a
µν
G
aµν
, d = 4 ,
O
Γ
=
¯
qΓq
¯
qΓq , d = 6 ,
O
σ
=m
¯
qσ
µν
λ
a
2
qG
a
µν
, d = 6 ,
O
f
= f
abc
G
a
µν
G
b
νγ
G
c
γµ
, d = 6 , etc. (7.202)
To evaluate (7.149) one must know the vacuum expectation values of all op-
erators and the corresponding Wilson coefficients, which can be calculated
perturbatively and will be discussed in detail below. But first we shall present
the general technique of QCD sum rules.
QCD sum rules start from the fact that the vacuum polarization tensor can
be described at the hadronic level, i.e., in terms of hadrons and hadronic reso-
nances. The optical theorem states that the total cross section of a certain reaction
16
See M.A. Shifmann, A.I. Vainshtein, and V.I. Zakharow: Nucl. Phys. B 147, 385 and
448 (1979).

7.2 QCD Sum Rules 491
equals the imaginary part of its forward-scattering amplitude. This can be un-
derstood from the fact that the cross section is proportional to the square of
some amplitude, graphically depicted by doubling the corresponding graph (see
Fig. 7.14).
The forward-scattering amplitude corresponds to the vacuum polarization
tensor. Hence for vector coupling we can write
ImΠ
V
s = q
2
=
9
64π
2
α
2
sσ
e
+
+e
−
→γ
∗
→hadrons
. (7.203)
Fig. 7.14. A graphical dem-
onstration of the optical the-
orem
The cross section of virtual photons decaying into hadrons has been exten-
sively studied in electron positron annihilation, e.g., at DESY in Hamburg and
at SLAC in Stanford. For low virtuality of the photon there is a contribution only
when q
2
is just the mass squared of a hadronic resonance with photon quan-
tum numbers, i.e., a 1
−−
resonance. (Here 1 is the spin, the first “−”represents
the internal parity, and the second “−” C parity. Only neutral particles have a C
parity.) Therefore the vacuum polarization tensor can be thought of as a sum of
δ functions of the type δ(q
2
−m
2
R
). In reality the hadronic states are rather broad
(see Fig. 7.15), but here they can be approximated by delta functions. Bear in
mind that, in principle, we can imagine inserting a Breit–Wigner form instead;
however, the precision achieved is such that it does not really make a difference.
As Π
V
is dimensionless, this must be multiplied by the only dimensional quan-
tity s = m
2
R
. All other constants appearing here are absorbed in a parameter g
R
,
and we have
Im
Π
V
(s = q
2
)
=
q
π
e
2
q
R
m
2
R
g
2
qR
δ
s −m
2
R
. (7.204)
Here the sum over resonances has been split into sums of resonances that require
the creation of a q
¯
qpairofflavorq.Forq = c these are, e.g., J/ψ, ψ
,ψ
, ···.
For sufficiently high virtualities of the photon, more than one particle can be
created, and discrete resonances are replaced by continua of states. For virtual-
ities just above the continuum threshold, the cross section cannot be expressed
in a general simple form. Above the continuum threshold this is possible, since
just the elementary e
+
+e
−
→q +
¯
q cross section can be inserted.
σ(e
+
+e
−
→hadrons) =
4πα
2
3s
q
e
2
q
. (7.205)
The ratio of the cross sections for multipion production and (7.153) are plotted
in Fig. 7.15.
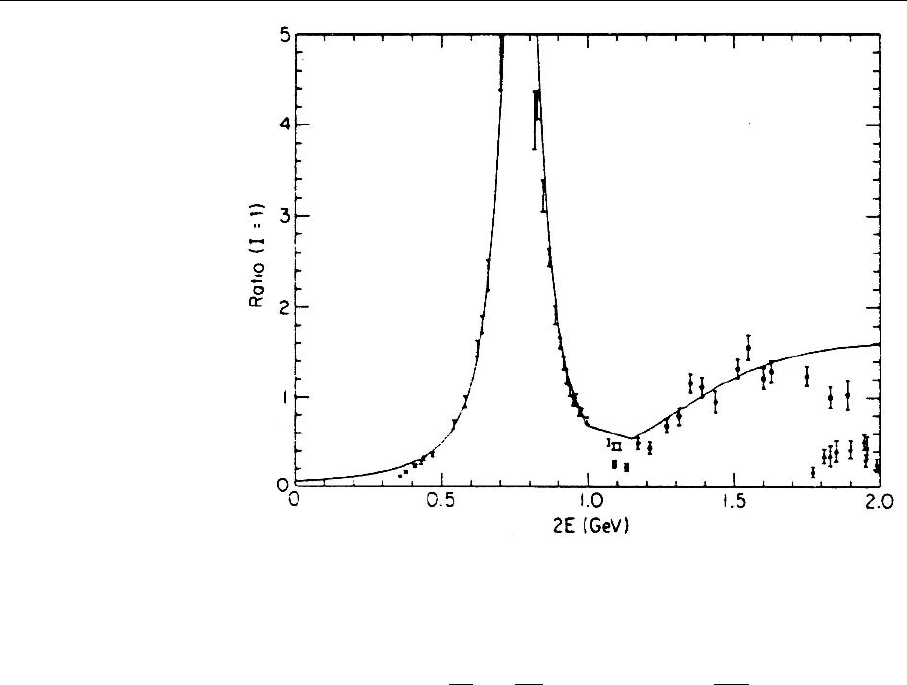
492 7. Nonperturbative QCD
Fig. 7.15. The ratio σ(e
+
e
−
→nπ) / σ(e
+
e
−
→µ
+
µ
−
)
The rho resonance at 770 MeV is very prominent, while the higher resonances
merge with the continuum. The continuum threshold s
0
is at about 1.3GeV.
Im
Π
V
(s = q
2
)
=
3π
e
2
f
R
m
2
R
g
2
R
δ
s −m
2
R
+
f
9
16π
e
2
f
Θ
s −s
0 f
.
(7.206)
Here we have counted each flavor f three times, since there are three colors.
The continuum thresholds s
0f
for the different flavors f can be taken to be free-
fitting parameters. In our case we take only up and down quarks into account
and choose s
0
=s
0u
= s
0d
≈ 1.3 GeV and neglect all except the resonance in
the first term on the right-hand side of (7.154). As we have already mentioned,
its approximation by the free-quark cross section is poor near the continuum
threshold, and one attempts to minimize the errors resulting from this by suitably
adjusting s
0 f
. In the following, we shall expand the correlator in (7.149) in the
framework of OPE and in this way obtain a representation of Π
V
as a function
of expectation values of certain operators. On the other hand, the imaginary
part of Π
V
can, as discussed above, be parametrized by discrete resonances
and a continuum contribution. This will enable us to express the mass of the
lightest resonance in terms of the expectation values mentioned above. This ap-
proach can be repeated for each J
PC
channel so that many masses (and coupling
constants) are fitted essentially by three expectation values. Our trust in this pro-
cedure is based primarily on its success. QCD sum rules consistently describe
7.2 QCD Sum Rules 493
a plethora of hadronic data, all of them with a typical accuracy of about 20%.
On the other hand, the fitted expectation values
-
0
α
s
π
G
a
µν
G
aµν
0
.
=(360 ±20 MeV)
4
,
,
0
¯
uu
0
=
-
0
¯
dd
0
.
=−(225 ±25 MeV)
3
,
,
0
m
s
¯
ss
0
=−(210 ±5MeV)
4
,
,
0
m
¯
qq
0
=−(100 MeV)
4
, m =
1
2
(m
u
+m
d
),
,
0
¯
qgσ
µν
G
aµν
q
0
=0.436 GeV
5
(7.207)
have far-reaching physical implications. They describe physical properties of the
nonperturbative QCD ground state and give, for example, the vacuum energy
density. To illustrate this, let us discuss the trace of the energy momentum tensor
of QCD,
Θ
µ
µ
=
β(g)
2g
G
a
µν
G
aµν
+
m
¯
qq , (7.208)
with the QCD beta function
β(g) =−
g
3
(4π)
2
11 −
2
3
N
f
+... . (7.209)
This gives, on inserting (7.209),
Θ
µ
µ
=−
1
8
11 −
2
3
N
f
α
s
π
G
a
µν
G
aµν
+
q
m
q
¯
qq , (7.210)
,
Θ
µ
µ
≈−(370 MeV)
4
. (7.211)
In the bag model Θ
µ
µ
is simply ( is the energy density, p is the pressure)
Θ
µ
µ
bag
= −3p =−4B , (7.212)
which suggests that the bag constant is (N
F
=3)
B =
9
32
-
α
s
π
G
a
µν
G
aµν
.
≈(260 MeV)
4
, (7.213)
which is substantially larger than the value fitted in the simple bag model (see
(3.151)) B = (146 MeV)
4
. There do exist a number of modified bag models with
a smaller bag radius and correspondingly larger B values. Some of them use B
as large as (250 MeV)
4
and their authors claim that the sum-rule value (7.213)
would support their model. Such claims are, however, not very sensible. Ad-
ditional interactions are introduced in each of these models. The energy and
pressure associated with these additional interactions and that due to the QCD
vacuum state are interwoven, such that is not so clear which quantity should

494 7. Nonperturbative QCD
be compared to (7.211). Most probably B should be regarded only as an effec-
tive parameter and the bag model as a simple model with limited connections to
QCD.
On the other hand, (7.211) is a clear statement of the fact that the vac-
uum of particle physics is far from being a simple empty state, but is instead
a complicated structure with a definite energy. To illustrate this fact let us
calculate the total energy content of a cubic meter of QCD vacuum:
1m
3
×(260 MeV)
4
=MeV ×260 ×
10
15
3
260 MeV fm
197 MeV fm
3
=6.0 ×10
47
MeV = 10
18
kg = 10
15
t . (7.214)
This corresponds to a mass energy of a million billions tonnes of matter. These
numbers become much more exotic if one studies astronomical distances.
Chiral symmetry, i.e. SU(2), plays an important and still not fully understood
role in full QCD. The normal isospin symmetry transformation is
ψ(x) →exp
−
i
2
α
a
(x)τ
a
ψ(x). (7.215)
In the absence of quark mass terms a second symmetry follows from this, namely
ψ(x) →exp
−
i
2
α
a
(x)τ
a
γ
5
ψ(x). (7.216)
The reason that
¯
ψ(x)γ
µ
ψ(x) is invariant is that γ
5
anticommutes with every
γ matrix, and thus any bilinear form with an even number of γ matrices between
ψ
†
(x) and ψ(x) is chirally symmetric, and all bilinear forms with an odd number
are not:
ψ
†
(x)γ
0
γ
µ
ψ(x) → ψ
†
(x) exp
i
2
α
a
(x)τ
a
γ
5
γ
0
γ
µ
exp
−
i
2
α
a
τ
a
γ
5
ψ(x)
=ψ
†
(x)γ
0
exp
−
i
2
α
a
(x)τ
a
γ
5
γ
µ
exp
−
i
2
α
a
τ
a
γ
5
ψ(x)
=ψ
†
(x)γ
0
γ
µ
exp
i
2
α
a
(x)τ
a
γ
5
exp
−
i
2
α
a
τ
a
γ
5
ψ(x)
=ψ
†
(x)γ
0
γ
µ
ψ(x). (7.217)
Consequently the quark-mass term m
q
¯
ψψ violates the symmetry (7.216), but
since the QCD up and down quark masses are small, their symmetry-breaking
effects should be weak, such that a symmetric theory should give a good descrip-
tion. Surprisingly this is not the case. While the up and down quark masses are
only about m
u
=5.6 ±1.1MeVandm
d
≈ 9.9 ±1.1 MeV, the chiral partners
and a
1
have vastly different masses
m
a
1
−m
=1260 MeV −770 MeV = 490 MeV , (7.218)
which implies that in addition to the small explicit breaking of chiral sym-
metry there must also be a spontaneous symmetry violation. “Spontaneous

7.2 QCD Sum Rules 495
symmetry breaking” (SSB) designates all cases in which a symmetry present
in the Lagrangian is not present in the actual physical ground state. Let us add
that has the J
PC
quantum numbers 1
−−
, while a
1
has 1
++
.Botharethe
lightest mesons with these quantum numbers. As (7.216) mixes vector states
with axial-vector states, and a
1
would have the same mass if (7.216) were
a symmetry operation. Similarily ω(m
ω
= 782 MeV, J
PC
=1
−−
) and f
1
(m
f
1
=
1282 MeV, J
PC
=1
++
) should be degenerate, etc. The pion, however, should
play a special role; see below. Let us also note that in lattice calculations (see
Sect. 7.1) the restoration of chiral symmetry at the phase transition manifests
itself by m
and m
a
1
converging to the same value. If (7.216) is a symmetry
operation, it follows that
Q
a
5
=
d
3
x
¯
ψ(x)γ
0
γ
5
1
2
τ
a
ψ(x) (7.219)
is an additional conserved quantity, similar to the total isospin
Q
a
=
d
3
x
¯
ψ(x)γ
0
1
2
τ
a
ψ(x). (7.220)
As (7.216) is a symmetry of the Lagrangian (neglecting quark masses for the
time being), |0,
ˆ
Q
5
|0,
ˆ
Q
2
5
|0, ... all have the same energy. On the other hand,
we have just argued that this symmetry is spontaneously broken for the ground
state; thus
ˆ
Q
5
|0=|v
1
=|0 ,
ˆ
Q
2
5
|0=|v
2
=|0 . (7.221)
Owing to all the other symmetries of the theory, |0, |v
1
, |v
2
,... can differ
only by the presence of
¯
qq pairs. To lowest order
G
0
¯
ψγ
µ
γ
5
τ
a
2
ψ
v
1
H
= 0 . (7.222)
We substitute φ
a
µ
(x) =
¯
ψ(x)γ
µ
γ
5
τ
a
2
ψ(x).Asφ
a
µ
(x) transforms as an isospin
vector we find that
φ
a
µ
(x) → φ
a
µ
(x) −iδα
A
(x)(T
A
)
ab
φ
b
µ
(x),
φ
a
µ
(x) → exp
iδα
b
(x)Q
b
5
φ
a
µ
(x) exp
−iδα
c
(x)Q
c
5
⇒φ
a
µ
(x) +iδ
A
α
(x)
Q
A
5
,φ
a
µ
(x)
⇒
T
A
ab
φ
b
µ
(x) =−
Q
A
5
,φ
a
µ
. (7.223)
Taking the vacuum expectation value of (7.223) yields
-
0
T
A
ab
φ
b
µ
(x)
0
.
=−
-
0|Q
A
5
φ
a
µ
|0
7
89:
=0
.
+
-
0|φ
a
µ
Q
A
5
|0
.
=
,
0
φ
a
µ
v
1
= 0 . (7.224)

496 7. Nonperturbative QCD
Obviously there must be at least one linear combination of the φ
b
(x) with
a nonvanishing vacuum expectation value. For SU(2) the number of generators
is three, just like the number of vector components. In fact the pions are a regular
representation of the SU(2). Therefore we shall not distinguish bestween A and
a indices. Let us define
δ
ab
σ = i
Q
a
5
,φ
b
. (7.225)
Equation (7.224) then implies that
i
-
0
Q
a
5
,φ
b
0
.
=0|σ|0 = 0 . (7.226)
To describe SSB, one usually introduces an effective field σ with a potential that
is minimal for a finite value σ . Here we have shown that even without specifying
an explicit model one must always have an effective σ term. Next we introduce
the pion in our scheme. Fourier transforming φ
a
µ
(x),weget
G
0
¯
ψ(p
)γ
µ
γ
5
τ
a
2
ψ( p)
v
1
H
= 0 . (7.227)
We assume that
¯
ψ,ψ are incoming or outgoing on-shell particles (either quarks
or nucleons). We then multiply this expression by q
µ
= p
µ
− p
µ
. On the other
hand, we know that |v
1
should be identified with some field. In principle
Q
5
|0=|v
1
could be related to any pseudoscalar, but for
[
H
0
, Q
5
]
=0 it follows that
H
0
|v
1
=+Q
5
H
0
|0=0 , (7.228)
such that in the absence of chiral symmetry breaking the particle must be
massless (it is the corresponding, so-called Goldstone boson). The pion, with
its extremely small mass (compared with other hadrons), is the only natural
candidate. Equation (7.227) thus implies that
G
0
¯
ψ(p
)( p/
− p/)γ
5
τ
a
2
ψ( p)
π
b
H
=
G
0
¯
ψ(p
)(mγ
5
+γ
5
p/)
τ
a
2
ψ( p)
π
b
H
=−im
-
0
¯
ψiγ
5
τ
a
ψ
π
b
.
∼δ
ab
= 0 . (7.229)
Transforming this back into coordinate space yields
G
0
∂
µ
¯
ψ(x)γ
µ
γ
5
τ
a
2
ψ
π
b
H
=
-
0
∂
µ
A
a
µ
π
b
.
= δ
ab
·const. = δ
ab
f
π
m
2
π
, (7.230)

7.2 QCD Sum Rules 497
with the usual definition of the pion decay constant f
π
. This relationship is pos-
tulated to hold at the operator level to give what is called a PCAC (partially
conserved axial vector current)
∂
µ
A
aµ
= f
π
m
2
π
π
a
. (7.231)
This equation implies that the violation of axial-vector current conservation can
be described as being due to the coupling to pions. Many interesting relations can
be deduced from this starting point. We are especially interested in the following:
I =
d
4
x e
−ik·x
-
0
T
∂
µ
A
a
µ
(0)∂
ν
A
b
ν
(x)
0
.
= f
2
π
m
4
π
d
4
x e
−ik·x
-
0
T
π
a
(0)π
b
(x)
0
.
= f
2
π
m
4
π
δ
ab
·iD
π
(k). (7.232)
We look at this in the limit k → 0
D
π
(k) = 1/
k
2
−m
2
π
→−1/m
2
π
and
obtain
I =−i f
2
π
m
2
π
δ
ab
. (7.233)
On the other hand, by partial integration we have
I(k → 0) =
d
4
x
−∂
ν
e
−ik·x
-
0
T
∂
µ
A
a
µ
(0)A
b
ν
(x)
0
.
−
d
4
x e
−ik·x
-
0
∂
ν
Θ(x
0
)A
b
ν
(x)∂
µ
A
a
µ
(0)
+∂
ν
Θ(−x
0
)∂
µ
A
a
µ
(0)A
b
ν
(x)
0
.
, (7.234)
I(k → 0) = 0−
d
4
x δ(x
0
)
-
0
A
b
0
(x), ∂
µ
A
a
µ
(0)
0
.
=−
d
4
x δ(x
0
)
-
0
A
b
0
(0), ∂
µ
A
b
µ
(−x)
0
.
=
d
3
x
-
0
A
b
0
(0, x), ∂
0
A
a
0
(0, 0)
0
.
, (7.235)
because only terms even in x contribute. As A
b
0
is not explicitly time dependent,
this becomes
I(k → 0) = i
d
3
x
-
0
A
b
0
(0, x),
A
a
0
(0, 0), H(0)
0
.
. (7.236)
This we shall evaluate for
H = H
0
+H
int
= H
0
+
d
3
y
m
u
¯
u(0, y)u(0, y) +m
d
¯
d(0, y)d(0, y)
(7.237)
with
q
+
α
(x, t), q
β
( y, t)
=δ
αβ
δ
3
(x −y). (7.238)

498 7. Nonperturbative QCD
By straightforward calculation (see Exercise 7.3) we get
-
0
A
b
0
(0, x),
A
b
0
(0, 0), H
int
(0)
0
.
=
G
0
m
u
+m
d
2
(
¯
uu +
¯
dd )
0
H
(7.239)
and thus
(m
u
+m
d
)0|
¯
uu +
¯
dd|0=−f
2
π
m
2
π
≈−2 ×(100 MeV)
4
. (7.240)
We have seen how the nonperturbative effects leading to the breaking of chi-
ral symmetry and thus to hadronic mass correction lead to the introduction of
a quark condensate (7.240). QCD sum rules invoke similar condensates to de-
scribe the nonperturbative effects of QCD. In general, here one has to allow for
the appearance of all possible condensates, of all the operators O
n
appearing in
(7.201). Let us now return to this equation.
EXERCISE
7.3 PCAC and the Quark Condensate
Problem. Calculate
-
0
A
b
0
(0, x),
A
a
0
(0, 0), m
u
¯
u( y)u( y) +m
d
¯
d( y)d( y)
0
.
d
3
x d
3
y
(1)
with
A
b
0
(x) =
¯
q(x)γ
0
γ
5
τ
b
2
q(x), q(x) =
u(x)
d(x)
. (2)
Solution. First we write
m
u
¯
u( y)u( y) +m
d
¯
d( y)d( y) =
m
u
+m
d
2
¯
q( y)q( y) +
m
u
−m
d
2
¯
q( y)τ
3
q( y)
(3)
and then we write, with simultaneous Lorentz and isospin indices α, β, γ, δ,
¯
q(0)
τ
a
2
γ
0
γ
5
q(0),
¯
q( y)q( y)
=
q
+
α
(0)q
β
(0), q
+
γ
( y)q
δ
( y)
τ
a
2
γ
5
αβ
(
γ
0
)
γδ
=
−q
+
α
q
+
γ
$
q
β
, q
δ
%
+q
+
α
q
β
q
+
γ
q
δ
−q
+
γ
$
q
+
α
, q
δ
%
q
β
+
q
+
α
, q
+
γ
q
δ
q
β
τ
a
2
γ
5
αβ
(
γ
0
)
γδ
(4)
7.2 QCD Sum Rules 499
as
(...)=−q
+
α
q
+
γ
q
β
q
δ
−q
+
α
q
+
γ
q
δ
q
β
+q
+
α
q
β
q
+
γ
q
δ
+q
+
α
q
+
γ
q
β
q
δ
−q
+
γ
q
+
α
q
δ
q
β
−q
+
γ
q
δ
q
+
α
q
β
+q
+
α
q
+
γ
q
δ
q
β
+q
+
γ
q
+
α
q
δ
q
β
=q
+
α
q
+
γ
q
δ
q
β
(+1−1 −1 +1 +1 −1) +
q
+
α
q
β
, q
+
γ
q
δ
. (5)
Now we use
$
q
β
(0, 0), q
δ
(0, y)
%
=0 =
q
+
α
(0, 0), q
+
γ
(0, y)
,
q
β
(0, 0), q
+
γ
(0, y)
=δ
βγ
δ
3
(y),
$
q
+
α
(0, 0), q
δ
(0, y)
%
=δ
αδ
δ
3
(y) (6)
to get
[... ,...]=δ
3
(y)
q
+
α
(0)q
δ
(0)
τ
a
2
γ
5
γ
0
αδ
−q
+
γ
(0)q
β
(0)
γ
0
τ
a
2
γ
5
γβ
=δ
3
(y)q
+
α
(0)q
δ
(0)
τ
a
γ
5
γ
0
αδ
. (7)
Similarly we obtain
¯
q(0)
τ
a
2
γ
0
γ
5
q(0),
¯
q(0, y)τ
3
q(0, y)
=δ
3
(y)
q
+
α
(0)q
δ
(0)
τ
a
2
γ
5
γ
0
τ
3
αδ
−q
+
γ
(0)q
β
(0)
γ
0
τ
3
τ
a
2
γ
5
γβ
=δ
3
(y)q
+
α
(0)q
δ
(0)
γ
5
γ
0
1
2
τ
a
,τ
3
7
89 :
δ
a3
αδ
(8)
and thus
d
3
y
A
a
0
(0, 0),
m
u
+m
d
2
¯
q(0, y)
11 q(0, y) +
m
u
−m
d
2
¯
q(0, y)τ
3
q(0, y)
=
m
u
+m
d
2
q
+
α
(0)q
δ
(0)
γ
5
γ
0
τ
a
αδ
+
m
u
−m
d
2
q
+
α
(0)q
δ
(0)
(
γ
5
γ
0
)
αδ
δ
a3
= J(0). (9)
The next step just repeats the preceding one:
d
3
x
A
b
0
(0, x), J(0)
=
d
3
r δ
3
(x)
m
u
+m
d
2
q
†
α
(0)q
δ
(0)
τ
b
2
γ
5
γ
5
γ
0
τ
a
−γ
5
γ
0
τ
a
τ
b
2
γ
5
αδ
+
m
u
−m
d
2
q
†
α
(0)q
δ
(0)
τ
b
2
γ
5
γ
5
γ
0
δ
a3
−γ
5
γ
0
δ
a3
τ
b
2
γ
5
αδ
Exercise 7.3
