Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


Contents
1. The Introduction of Quarks .............................. 1
1.1 TheHadronSpectrum ............................. 1
2. Review of Relativistic Field Theory ........................ 17
2.1 Spinor Quantum Electrodynamics ..................... 17
2.1.1 TheFreeDiracEquationandItsSolution ......... 17
2.1.2 DensityandCurrentDensity .................. 20
2.1.3 CovariantNotation ......................... 21
2.1.4 NormalizationofDiracSpinors ................ 22
2.1.5 Interaction with a Four-Potential A
µ
............. 24
2.1.6 Transition Amplitudes ....................... 25
2.1.7 DiscreteSymmetries ........................ 25
2.2 Scalar Quantum Electrodynamics ..................... 26
2.2.1 The Free Klein–Gordon Equation and its Solutions . . 26
2.2.2 Interaction of a π
+
with a Potential A
µ
.......... 29
2.2.3 π
+
K
+
Scattering ........................... 32
2.2.4 TheCrossSection .......................... 35
2.2.5 Spin-1ParticlesandTheirPolarization ........... 47
2.2.6 ThePropagatorforVirtualPhotons .............. 53
2.3 Fermion–Boson and Fermion–Fermion Scattering ......... 58
2.3.1 Traces and Spin Summations .................. 60
2.3.2 The Structure of the Form Factors
fromInvarianceConsiderations ................ 70
3. Scattering Reactions and the Internal Structure of Baryons ..... 77
3.1 SimpleQuarkModelsCompared ..................... 77
3.2 TheDescriptionofScatteringReactions ................ 80
3.3 TheMITBagModel ..............................125
4. Gauge Theories and Quantum-Chromodynamics .............155
4.1 TheStandardModel:ATypicalGaugeTheory ...........155
4.2 TheGaugeTheoryofQuark–QuarkInteractions ..........165
4.3 DimensionalRegularization .........................184
4.4 TheRenormalizedCouplingConstantofQCD ...........203
4.5 ExtendedExample:AnomaliesinGaugeTheories.........220
4.5.1 TheSchwingerModelontheCircle .............220
4.5.2 DiracSea ................................222

XII Contents
4.5.3 UltravioletRegularization ....................225
4.5.4 StandardDerivation .........................228
4.5.5 AnomaliesinQCD .........................231
4.5.6 TheAxialandScaleAnomalies ................232
4.5.7 Multiloop Corrections .......................238
5. Perturbative QCD I: Deep Inelastic Scattering ...............239
5.1 The Gribov–Lipatov–Altarelli–Parisi Equations ...........239
5.2 AnAlternativeApproachtotheGLAPEquations .........265
5.3 Common Parametrizations of the Distribution Functions
andAnomalousDimensions .........................281
5.4 RenormalizationandtheExpansionIntoLocalOperators....292
5.5 CalculationoftheWilsonCoefficients .................328
5.6 TheSpin-DependentStructureFunctions ...............356
6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics 387
6.1 TheDrell–YanProcess .............................387
6.2 Small-x Physics ..................................430
7. Nonperturbative QCD ..................................441
7.1 Lattice QCD Calculations . . . ........................442
7.1.1 ThePathIntegralMethod .....................442
7.1.2 ExpectationValues .........................447
7.1.3 QCD on the Lattice . ........................449
7.1.4 Gluons on the Lattice ........................451
7.1.5 IntegrationinSU(2) .........................454
7.1.6 Discretization:ScalarandFermionicFields .......456
7.1.7 FermionicPathIntegral ......................461
7.1.8 MonteCarloMethods .......................463
7.1.9 MetropolisAlgorithm .......................465
7.1.10 LangevinAlgorithms ........................466
7.1.11 The Microcanonical Algorithm ................468
7.1.12 StrongandWeakCouplingExpansions ...........474
7.1.13 Weak-CouplingApproximation ................476
7.1.14 Larger Loops in the Limit
ofWeakandStrongCoupling .................477
7.1.15 TheStringTension .........................479
7.1.16 The Lattice at Finite Temperature ...............482
7.1.17 The Quark Condensate .......................485
7.1.18 ThePolyakovLoop .........................487
7.1.19 TheCenterSymmetry .......................488
7.2 QCDSumRules .................................490
8. Phenomenological Models for Nonperturbative QCD Problems . . 515
8.1 The Ground State of QCD . . ........................515
8.2 TheQuark–GluonPlasma ..........................530

Contents XIII
Appendix ...............................................541
A The Group SU(N) ................................541
B Dirac Algebra in Dimension d .......................543
C SomeUsefulIntegrals .............................546
Subject Index ............................................549

Contents of Examples and Exercises
1.1 The Fundamental Representation of a Lie Algebra ............ 11
1.2 Casimir Operators of SU(3) ............................ 15
2.1 TheMatrixElementforaPionScatteredbyaPotential ........ 31
2.2 TheFluxFactor ..................................... 37
2.3 The Mandelstam Variable s ............................ 38
2.4 TheLorentz-InvariantPhase-SpaceFactor.................. 39
2.5 π
+
π
+
and π
+
π
−
Scattering............................ 41
2.6 The Cross Section for Pion–Kaon Scattering ................ 43
2.7 PolarizationStatesofaMassiveSpin-1Particle.............. 49
2.8 ComptonScatteringbyPions ........................... 54
2.9 Elastic e
−
π
+
Scattering(I)............................. 58
2.10 FeaturesofDiracMatrices ............................. 63
2.11 Electron–PionScattering(II) ........................... 66
2.12 Positron–Pion Scattering .............................. 69
2.13 Electron–MuonScattering ............................. 73
3.1 NormalizationandPhaseSpaceFactors ................... 87
3.2 Representation of W
µν
by Electromagnetic Current Operators . . . 88
3.3 TheNucleonicScatteringTensorwithWeakInteraction........ 91
3.4 The Inclusive Weak Lepton–Nucleon Scattering ............. 94
3.5 The Cross Section as a Function of x and y ................. 99
3.6 TheBreitSystem ....................................112
3.7 TheScatteringTensorforScalarParticles ..................113
3.8 Photon–Nucleon Scattering Cross Sections
forScalarandTransversePhotonPolarization ...............115
3.9 A Simple Model Calculation
for the Structure Functions of Electron–Nucleon Scattering .....118
3.10 AntiquarkSolutionsinaBag ...........................127
3.11 TheBagWaveFunctionforMassiveQuarks ................135
3.12 Gluonic Corrections to the MIT Bag Model .................143
3.13 TheMeanChargeRadiusoftheProton ....................146
3.14 TheMagneticMomentoftheProton......................149
4.1 TheGeometricFormulationofGaugeSymmetries............158
4.2 TheFeynmanRulesforQCD ...........................172
4.3 Fadeev–PopovGhostFields ............................178
4.4 The Running Coupling Constant .........................180
4.5 The d-DimensionalGaussianIntegral .....................189

XVI Contents of Examples and Exercises
4.6 The d-DimensionalFourierTransform ....................198
4.7 FeynmanParametrization ..............................201
5.1 PhotonandGluonPolarizationVectors ....................244
5.2 More about the Derivation of QCD Corrections
to Electron–Nucleon Scattering . ........................245
5.3 TheBremsstrahlungPartoftheGLAPEquation .............260
5.4 TheMaximumTransverseMomentum ....................267
5.5 Derivation of the Splitting Function P
Gq
...................269
5.6 Derivation of the Splitting Function P
qq
...................276
5.7 Derivation of the Splitting Function P
qG
...................277
5.8 Calculation of Moments of Splitting Functions
(AnomalousDimensions)..............................288
5.9 Decomposition Into Vector and Axial Vector Couplings ........296
5.10 The Proof of (5.148) .................................300
5.11 The Lowest-Order Terms of the β Function .................308
5.12 TheMomentsoftheStructureFunctions ...................315
5.13 Calculation of the Gluonic Contribution to F
L
(x, Q
2
) .........338
5.14 Calculation of Perturbative Corrections to Structure Functions
withtheCross-SectionMethod..........................346
5.15 Calculation of the Gluonic Contribution to F
L
withtheCross-SectionMethod..........................354
5.16 HigherTwistinDeepInelasticScattering ..................366
5.17 PerturbationTheoryinHigherOrdersandRenormalons .......370
6.1 TheDrell–YanCrossSection ...........................409
6.2 TheOne-GluonContributiontotheDrell–YanCrossSection ....410
6.3 The Drell–Yan Process as Decay of a Heavy Photon ..........411
6.4 Heavy Photon Decay Into Quark, Antiquark, and Gluon ........413
6.5 FactorizationinDrell–Yan .............................419
6.6 Collinear Expansion and Structure Functions
inDeepInelasticLepton–NucleonScattering ...............427
7.1 Derivation of the Transition Amplitude (7.5) ................445
7.2 TheAverageLinkValue ...............................470
7.3 PCAC and the Quark Condensate ........................498
7.4 Calculation of QCD Sum-Rule Graphs with
DimensionalRegularization ............................504
8.1 TheQCDVacuumEnergyDensity .......................521
8.2 TheQCDGroundStateandtheRenormalizationGroup .......527
8.3 TheQGPasaFreeGas ...............................529

1. The Introduction of Quarks
About 70 years ago, only a small number of “elementary particles”,
1
thought
to be the basic building blocks of matter, were known: the proton, the electron,
and the photon as the quantum of radiation. All these particles are stable (the
neutron is stable only in nuclear matter, the free neutron decays by beta decay:
n → p +e
−
+
¯
ν). Owing to the availability of large accelerators, this picture of
a few elementary particles has profoundly changed: today, the standard reference
Review of Particle Properties
2
lists more than 100 particles. The number is still
growing as the energies and luminosities of accelerators are increased.
1.1 The Hadron Spectrum
The symmetries known from classical and quantum mechanics can be utilized
to classify the “elementary-particle zoo”. The simplest baryons are p and n; the
simplest leptons e
−
and µ
−
. Obviously there are many other particles that must
be classified as baryons or leptons.
The symmetries are linked to conserved quantum numbers such as the
baryon number B, isospin T with z component T
3
, strangeness S, hypercharge
Y = B +S,chargeQ = T
3
+Y/2, spin I with z component I
z
, parity π,and
charge conjugation parity π
c
. Conservation laws for such quantum numbers
manifest themselves by the absence of certain processes. For example, the hy-
drogen atom does not decay into two photons: e
−
+p →γ +γ, although this
process is not forbidden either by energy–momentum conservation or by charge
conservation. Since our world is built mainly out of hydrogen, we know from
our existence that there must be at least one other conservation law that is as
fundamental as charge conservation. The nonexistence of the decays n →p +e
−
and n → γ +γ also indicates the presence of a new quantum number. The proton
and neutron are given a baryonic charge B = 1, the electron B = 0. Similarly the
electron is assigned leptonic charge L =1, the nucleons L = 0. From the prin-
ciple of simplicity it appears very unsatisfactory to regard all observed particles
1
For a detailed discussion of the content of this chapter see W. Greiner and B. Müller:
Symmetries (Springer, Berlin, Heidelberg 1994).
2
See the Review of Particle Physics by W.-M. Yao et al., Journal of Physics G 33
(2006) 1, and information available online at http://pdg.lbl.gov/
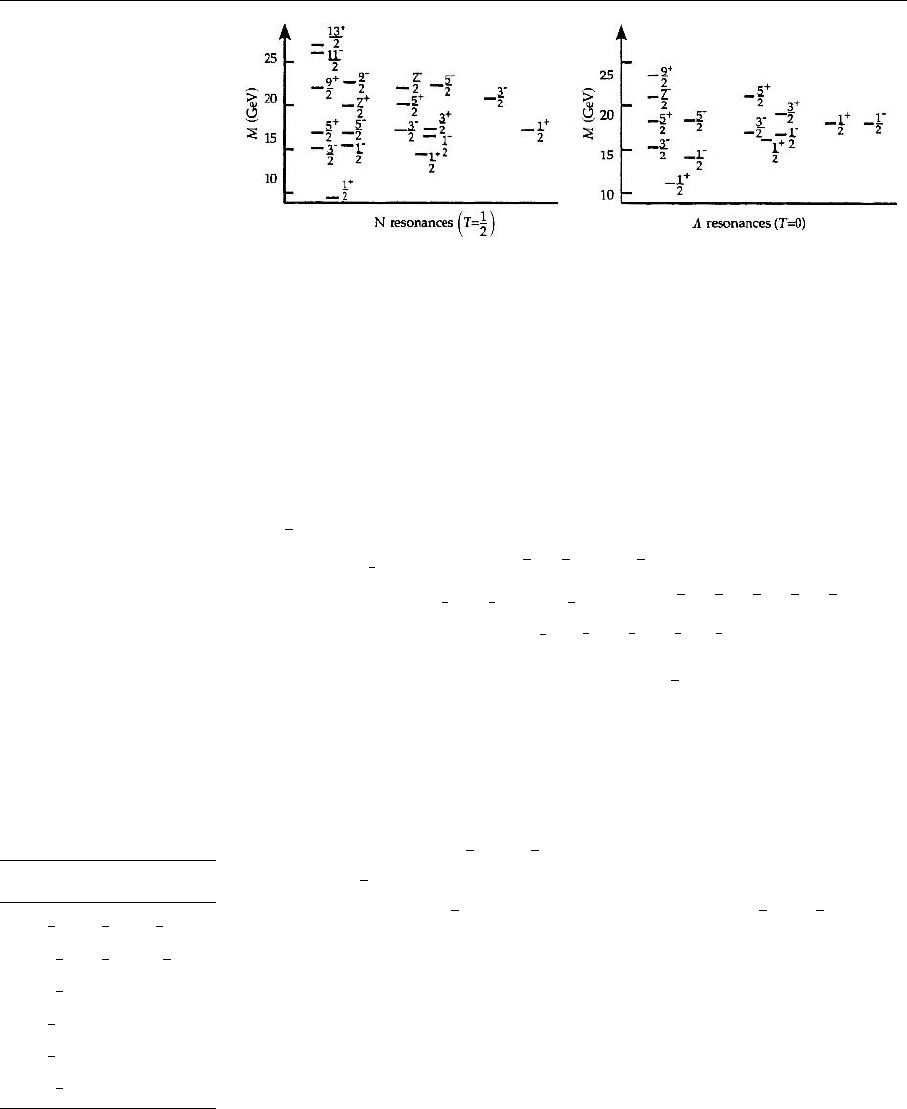
2 1. The Introduction of Quarks
Fig. 1.1. The mass spectra
of baryons. Plotted are the
average masses of the multi-
plets. For example, the state
N
5/2
+
at 1.68 MeV stands
for two particles, one pro-
tonlike and one neutronlike,
both with spin 5/2 and pos-
itive internal parity. The
figure contains 140 particle
states in total
Table 1.1. Quark charge (Q),
isospin (T, T
3
), and strange-
ness (S)
QTT
3
S
u
2
3
1
2
1
2
0
d −
1
3
1
2
−
1
2
0
s −
1
3
00−1
c
2
3
000
t
2
3
000
b −
1
3
000
as elementary. To give an impression of the huge number of hadrons known to-
day, we have collected together the baryon resonances in Fig. 1.1. The data are
taken from the “Review of Particle Properties”. Particles for which there is only
weak evidence or for which the spin I and internal parity P have not been de-
termined have been left out. Note that each state represents a full multiplet. The
number of members in a multiplet is N = 2T +1 with isospin T . Thus the 13 ∆
resonances shown correspond to a total of 52 different baryons.
When looking at these particle spectra, one immediately recognizes the sim-
ilarity to atomic or nuclear spectra. One would like, for example, to classify the
nucleon resonances (N resonances) in analogy to the levels of a hydrogen atom.
The
1
2
+
ground state (i.e., the ordinary proton and neutron) would then corres-
pond to the 1s
1
2
state, the states
3
2
−
,
1
2
−
,and
1
2
+
at approximately 1.5GeV to
the hydrogen levels 2p
3
2
,2p
1
2
,and2s
1
2
, the states
5
2
+
,
3
2
+
,
3
2
−
,
1
2
−
,
1
2
+
to the
sublevels of the third main shell 3d
5
2
,3d
3
2
,3p
3
2
,3p
1
2
,3s
1
2
, and so on.
Although one should not take this analogy too seriously, it clearly shows that
a model in which the baryons are built from spin-
1
2
particles almost automati-
cally leads to the states depicted in Fig. 1.1. The quality of any such model is
measured by its ability to predict the correct energies. We shall discuss specific
models in Sect. 3.1.
We therefore interpret the particle spectra in Fig. 1.1 as strong evidence that
the baryons are composed of several more fundamental particles and that most
of the observable baryon resonances are excitations of a few ground states. In
this way the excited states
3
2
−
and
1
2
−
are reached from the nucleon ground state
N(938 MeV)
1
2
+
by increasing the angular momentum of one postulated com-
ponent particle by one:
1
2
+
can be coupled with 1
−
to give
1
2
−
or
3
2
−
.Asthe
energy of the baryon resonances increases with higher spin (i.e., total angular
momentum of all component particles), one can deduce that all relative orbital
angular momenta vanish in the ground states.
To investigate this idea further, one must solve a purely combinatorial prob-
lem: How many component particles (called quarks in the following) are needed,
and what properties are required for them to correctly describe the ground states
of the hadron spectrum? It turns out that the existence of several quarks must be
postulated. The quantum numbers given in Table 1.1 must be given to them.

1.1 The Hadron Spectrum 3
The three light quarks u, d, s can be identified with the three states in the fun-
damental representation of SU(3). This is initially a purely formal act. It gains
importance only as one shows that the branching ratios of particle reactions and
the mass differences between stable baryons show – at least approximately – the
same symmetries. This means that the so-called flavor SU(3) can be interpreted
as the symmetry group of a more fundamental interaction.
Hadrons are therefore constructed as flavor SU(3) states. As the spin of
the quarks must also be taken into account, the total symmetry group becomes
SU(3) ×SU(2). As an example we give the decomposition of the neutron into
quark states
3
:
|
n↑
=
1
√
18
2
|
d↑
|
d↑
|
u↓
−
|
d↑
|
d↓
|
u↑
−
|
d↓
|
d↑
|
u↑
−
|
d↑
|
u↑
|
d↓
+2
|
d↑
|
u↓
|
d↑
−
|
d↓
|
u↑
|
d↑
−
|
u↑
|
d↑
|
d↓
−
|
u↑
|
d↓
|
d↑
+2
|
u↓
|
d↑
|
d
↑
. (1.1)
Particularly interesting for the topic of this volume are the corresponding
decompositions of the states Ω
−
, ∆
++
,and∆
−
(see
3
):
Ω
−
=
|
s↑
|
s↑
|
s↑
,
∆
++
=
|
u↑
|
u↑
|
u↑
,
∆
−
=
|
d↑
|
d↑
|
d↑
. (1.2)
To obtain the spin quantum numbers of hadrons, one must assume that the quarks
have spin
1
2
. This poses a problem: spin-
1
2
particles should obey Fermi statis-
tics, i.e., no two quarks can occupy the same state. So the three quarks in Ω
−
,
∆
++
,and∆
−
must differ in at least one quantum number, as we shall discuss
in Chapt. 4. Before proceeding to the composition of baryons from quarks, we
shall first repeat the most important properties of the symmetry groups SU(2)
and SU(3).
SU(2) and SU(3) are special cases of the group SU(N) the special uni-
tary group in N dimensions. Any unitary square matrix
ˆ
U with N rows and
N columns can be written as (for more details see
3
)
ˆ
U =e
i
ˆ
H
, (1.3)
where
ˆ
H is a Hermitian matrix. The matrices
ˆ
U form the group SU(N) of unitary
matrices in N dimensions.
ˆ
H is Hermitian, i.e.,
ˆ
H
∗
ij
=
ˆ
H
ji
. (1.4)
Of the N
2
complex parameters (elements of the matrices), N
2
real parameters
for
ˆ
H and hence for
ˆ
U remain, owing to the auxiliary conditions (1.4). Since
ˆ
U
3
W. Greiner and B. Müller: Quantum Mechanics: Symmetries (Springer, Berlin, Heidel-
berg, 1994).

4 1. The Introduction of Quarks
is unitary, i.e.
ˆ
U
†
ˆ
U = 1, det
ˆ
U
†
det
ˆ
U =(det
ˆ
U)
∗
det
ˆ
U =1 and thus
det
ˆ
U
= 1 . (1.5)
Owing to (1.4), tr
ˆ
H
=α (α real) and
det
ˆ
U =det
e
i
ˆ
H
= e
itr
ˆ
H
= e
iα
. (1.6)
If we additionally demand the condition
det
ˆ
U =+1 , (1.7)
i.e., α = 0mod2π, only N
2
−1 parameters remain. This group is called the
special unitary group in N dimensions (SU(N)).
Let us now consider a group element
ˆ
U of U(N) as a function of N
2
parameters φ
µ
(µ = 1,... ,n). To this end, we write (1.3) as
ˆ
U(φ
1
,... ,φ
n
) = exp
−i
µ
φ
µ
ˆ
L
µ
, (1.8)
where
ˆ
L
µ
are for the time being unknown operators:
−i
ˆ
L
µ
=
∂
ˆ
U(φ)
∂φ
µ
φ=0
(1.9)
(φ = (φ
1
,... ,φ
n
)). For small φ
µ
(δφ
µ
) we can expand
ˆ
U in a series (11isthe
N × N unit matrix):
ˆ
U(φ) ≈
11 −i
n
µ=1
δφ
µ
ˆ
L
µ
−
1
2
µ,ν
δφ
µ
δφ
ν
ˆ
L
µ
ˆ
L
µ
+... . (1.10)
Boundary conditions (1.4) and (1.5) imply after some calculation that the
operators
ˆ
L
i
must satisfy the commutation relations
ˆ
L
i
,
ˆ
L
j
= c
ijk
ˆ
L
k
. (1.11)
Equation (1.11) defines an algebra, the Lie algebra of the group U(N).
The operators
ˆ
L
i
generate the group by means of (1.10) and are thus called
generators. Obviously there are as many generators as the group has parameters,
i.e., the group U(N) has N
2
generators and the group SU(N) has N
2
−1. The
quantities c
ijk
are called structure constants of the group. They contain all the
information about the group. In the Lie algebra of the group (i.e., the
ˆ
L
k
), there
is a maximal number R of commutating elements
ˆ
L
i
(i = 1,... ,R)
ˆ
L
i
,
ˆ
L
j
= 0 (i =1,... ,R). (1.12)
R is called the rank of the group. The eigenvalues of the
ˆ
L
i
are, as we shall see,
used to classify elementary-particle spectra. We shall now discuss the concepts

1.1 The Hadron Spectrum 5
introduced here using the actual examples of the spin and isospin group SU(2)
and the group SU(3).
SU(2).U(2) is the group of lineary independent Hermitian 2 ×2 matrices.
A well-known representation of it is given by the Pauli matrices and the unit
matrix
ˆ
σ
1
=
01
10
,
ˆ
σ
2
=
0 −i
i0
,
ˆ
σ
3
=
10
0 −1
, 11 =
10
01
. (1.13)
These span the space of Hermitian 2 ×2 matrices, i.e., they are linearly indepen-
dent. SU(2) has only three generators; the unit matrix is not used. From (1.3) we
can write a general group element of the group SU(2) as
ˆ
U(φ) = exp
−i
3
i=1
φ
i
ˆ
σ
i
(1.14)
(or, using the summation convention, exp(−iφ
i
ˆ
σ
i
)). Here φ = (φ
1
,φ
2
,φ
3
) is
a shorthand for the parameter of the transformation. The Pauli matrices satisfy
the commutation relations
ˆ
σ
i
,
ˆ
σ
j
=2iε
ijk
ˆ
σ
k
, (1.15)
with
ε
ijk
=
⎧
⎪
⎨
⎪
⎩
0 for two equal indices,
1 for even permutations of the indices,
−1 for odd permutations of the indices.
Usually, instead of
ˆ
σ
i
,the
ˆ
S
i
=
1
2
ˆ
σ
i
are used as generators, i.e.
ˆ
S
i
,
ˆ
S
j
= iε
ijk
ˆ
S
k
.
According to (1.11), iε
ijk
are the structure constants of SU(2). Equation (1.15)
shows that no generator commutes with any other, i.e., the rank of SU(2) is 1.
According to the Racah theorem, the rank of a group is equal to the number of
Casimir operators (i.e., those operators are polynomials in the generators and
commute with all generators). Thus there is one Casimir operator for SU(2),
namely the square of the well-known angular momentum (spin) operator:
ˆ
C
SU(2)
=
3
i=1
ˆ
S
2
i
. (1.16)
The representation of SU(2) given in (1.13) (and generally of SU(N))by
2 ×2 matrices (generally N ×N matrices) is called the fundamental represen-
tation of SU(2) (SU(N)). It is the smallest nontrivial representation of SU(2)
(SU(N)). It is a 2 ×2 representation for SU(2),a3×3 representation for SU(3),
