Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

26 2. Review of Relativistic Field Theory

Table 2.1. The behavior of the currents (2.53) under the transformations

T ,and

O =

S(x) V

(x) T

µν

(x) P(x) A

(x)

PS(

x) V

(

x) T

µν

(

x) −P(

x) −A

(

CS(x) −V

(x) −T

µν

(x) P(x) A

(x)

TS(−

x) V

(−

x) −T

µν

(−

x) −P(−

x) A

(−

OS(−x) −V

(−x) T

µν

(−x) P(−x) −A

(−x)

We also give the corresponding transformations for the electromagnetic four-

potential A

(x)

= A

(x),

(x)

=−A

(x),

(x)

= A

(−x),

(x)

=−A

(−x). (2.62)

2.2 Scalar Quantum Electrodynamics

2.2.1 The Free Klein–Gordon Equation and its Solutions

It is known that pions as spin-0 particles satisfy the Klein–Gordon equation. Here

we compile the main results of pion quantum electrodynamics. Starting from the

four-momentum vector and relativistic energy conservation

= (E, p), (2.63)

= E

− p

= m

(2.64)

and the correspondence between momentum and momentum operator

→

=i∂

, (2.65)

the free Klein–Gordon equation follows:



−m



φ(x, t) = 0 , (2.66a)

which can be written as



 +m



φ(x, t) = 0 (2.66b)

using the d’Alembertian operator (quabla operator), which is deﬁned by

 ≡ ∂

∂

∂t

−∇

. (2.67)

2.2 Scalar Quantum Electrodynamics 27

Plane waves of the form

φ(x, t) = Ne

−i p·x

= Ne

−i(Et−p·x)

(2.68)

are solutions of (2.66) if condition (2.64) is satisﬁed. Therefore we also have

solutions of positive and negative energy:

E =±



. (2.69)

The question of their interpretation is thus raised. To answer it, we shall derive

expressions for the probability density  and the probability current density j

by multiplying (2.66) by φ

∗

and its complex conjugate-equation by φ and

subtracting each from the other. This leads to the continuity equation (∂

≡

∂

∂t

)

∂

 +∇ · j = 0 , (2.70)

where

 = i



∗

(∂

φ) −(∂

∗

)φ



(2.71a)

and

j =−i



∗

(∇φ) −(∇φ

∗

)φ



. (2.71b)

In four-dimensional notation, this is concisely written as

∂

= 0 , (2.72)

with the four-current density

= (, j) = i



∗



∂



−



∂

∗





. (2.73)

The three-current density j in (2.71b) is formally identical with that known

from the Schrödinger equation. However, the probability density  contains, in

contrast to the Schrödinger density, additional time derivatives. This has the con-

sequence that  is not positive deﬁnite, which can be immediately checked using

plane waves (2.68), taking into account (2.69). In this way it follows for (2.71a)

that

 = 2

E . (2.74)

The probability current density (2.71b) is obtained as

j = 2

p . (2.75)

Since E can be positive or negative owing to (2.69), the above statement about 

is obvious. To interpret  nonetheless as a probability, one must make use of the

particle–antiparticle interpretation. By the Feynman–Stückelberg prescription, it

holds that:

A solution of negative energy for a particle pr opagating backward in time

corresponds to a solution of positive energy for an antiparticle pr opagating

forward in time.

The Klein–Gordon equation describes both neutral and charged mesons. In

the case of charged scalar particles we not only have to analyze their spatial

28 2. Review of Relativistic Field Theory

Fig. 2.1. Double scattering

of a particle (π

) off a po-

tential

Fig. 2.2. Scattering back-

ward in time: The par-

ticle here has, according to

Stückelberg and Feynman,

negative energy

Fig. 2.3. Feynman’s reinter-

pretation of the scattering

process shown in Fig. 2.2

Fig. 2.4. Emission of a π

−

with (E > 0, p) by the sys-

tem S

propagation but also the assignment of charges as discussed next for the charged

pions π

and π

−

. To this end we consider the scattering of a particle (e.g., a π

)

off a potential in second-order perturbation theory. The space–time diagram of

such a process is shown in Fig. 2.1. An incoming π

scatters off the potential

at position x

and time t

and propagates to position x

, where it scatters again

at a later time t

 t

and then moves on freely. According to Stückelberg and

Feynman there must be the possibility that particles are scattered backward in

time (Fig. 2.2). Thus one must allow in relativistic quantum ﬁeld theory for the

processes shown in the these ﬁgures.

We interpret this second process according to Feynman in such a way that

particle solutions of positive energy propagate exclusively forward and particle

solutions of negative energy exclusively backward in time. The π

moving back-

ward in time between t

and t

must have negative energy. It is equivalent to

a π

−

(antiparticle) moving forward in time. This is obviously implied by charge

conservation: only particle–antiparticle pairs can be created or annihilated. Fig-

ure 2.3 illustrates this reinterpretation of Fig. 2.2. At t

,aπ

−

pair is created

whose π

−

– which is identical to the originally incoming π

– is annihilated at

and whose π

propagates on.

There is also another way to demonstrate the concept of a charged Klein–

Gordon ﬁeld. The charged currents for π

and π

−

at positive energy are obtained

by multiplying the charge density (2.74), calculated for waves by positive energy,

by the positive and negative unit charge (e > 0), respectively, that is

(π

) = (±e) ×probability current density

for a π

at positive energy. (2.76)

Inserting the plane wave (2.68) into (2.71), we have

(π

) = (+e)2





, p



(2.77)

and

(π

−

) = (−e)2





, p



. (2.78)

Comparing (2.78) with (2.77), we see that it is obvious that (2.78) can also be

written as

(π

−

) = (+e)2



−



, −p



, (2.79)

which equals the current density of a π

with negative energy and nega-

tive momentum. In other words, a π

−

thus corresponds to a π

with inverse

four-momentum.

This correspondence can be expressed more precisely: if a system S emits a

−

of positive energy E > 0 and momentum p (see Fig. 2.4), the energy of S

is reduced by E, its momentum by p, and its charge by (−e). But all this is

2.2 Scalar Quantum Electrodynamics 29

equivalent to the absorption of a π

with negative four-momentum (−E, −p),

as demonstrated in Fig. 2.5. We summarize this with the following statement:

The emission (absorption) of an antiparticle with four-momentum p

is phys-

ically equivalent to the absorption (emission) of a particle with four-momentum

−p

2.2.2 Interaction of a π

with a Potential A

Just as in the case of the Dirac equation, the electromagnetic potential A

coupled in by the minimal-coupling prescription (π

has the charge +e)

∂

→∂

+ieA

(2.80)

to preserve gauge invariance. If this is inserted into (2.66b), one obtains the

Klein–Gordon equation with electromagnetic interaction

(

 +m

)φ =−ie(∂

+ A

∂

)φ +e

φ ≡−

V φ. (2.81)

In contrast to the Dirac theory, a coupling term quadratic in A

appears. How-

ever, we shall neglect it whenever scattering processes are considered in lowest

order. In this approximation the coupling potential reduces to

V (x) = ie(∂

(x) + A

(x)∂

). (2.82)

To calculate scattering processes, we also need the scattering amplitude. This is

for scattering in ﬁrst order of a potential

V , as before, given by

(1)

=−i

x φ

∗

V φ

. (2.83)

It is displayed by the graph in Fig. 2.6.

We shall now calculate the transition amplitude (2.83). Incoming and outgo-

ing π

states are described by plane waves

−i p

·x

, (2.84a)

−i p

·x

. (2.84b)

Together with (2.82), (2.83) becomes

(1)

=−iN

x e

i p

·x

(ie)(∂

+ A

∂

−i p

·x

=−ieN

( p

+ p

)

x e

−iq·x

(x)

=−ieN

( p

+ p

)

(q), (2.85)

Fig. 2.5. Reinterpretation

of the emission process in

Fig. 2.4 as an absorption

process

Fig. 2.6. π

scattering off a

potential V to lowest order.

The potential is denoted by

the vertex x

30 2. Review of Relativistic Field Theory

where the four-momentum transfer

q = p

− p

(2.86)

has been introduced. Also, in calculating (2.85), a partial integration of the type

+∞

−∞

= fg



∞

−∞

−

∞

−∞

d f

g (2.87)

has been performed twice. Here the assumption has been made that contributions

of the form gf vanish at inﬁnity, i.e.,



∞

−∞

= 0 . (2.88)

This requires that either the potentials A

or the wave amplitudes decay fast

enough at inﬁnity. Exact plane waves do not have this property. But, strictly

speaking, any particle is always represented by a wave packet. Even if it can be,

for large distances from the scattering center and for large times before or after

the scattering, arbitrarily delocalized; it will, however, decay asymptotically.

Taking into account that we use plane waves (2.84) just to simplify calculations,

the surface contributions can be neglected and the S-matrix element (2.83) can

be written in a more convenient form:

(1)

x φ

∗

(∂

+ A

∂

)φ



−(∂

∗

)φ

+φ

∗

(∂

)



=−i

(π

. (2.89)

Here

(π

) = ie



∗



∂



−



∂

∗





(2.90)

is the transition current density for the π

meson. For plane waves (2.84) this is

particularly simple:

(π

) = eN

( p

+ p

)

i( p

−p

)·x

, (2.91)

which also appears in (2.85). In the following problem (2.1), the steps discussed

here are illustrated once more.

2.2 Scalar Quantum Electrodynamics 31

EXERCISE

2.1 The Matrix Element for a Pion Scattered by a Potential

Problem. Consider the matrix element

dt e

i p

·x



∂

(x) + A

(x)∂



−i p

·x

. (1)

Assume that the four-potential fulﬁlls the conditions

(x, t) → 0fort →±∞, (2a)

A(x, t)

→0for

→∞, (2b)

and show that

(a)

dt e

i p

·x

∂



−i p

·x





−i(p

)



dt e

i p

·x

−i p

·x

, (3)

(b)

x e

i p

·x

∇ ·



−i p

·x



= i p

x e

i p

·x

−i p

·x

, (4)

and therefore also

(c)

x e

i p

·x



∂

+ A

∂



−i p

·x

=−i( p

+ p

)

x e

i p

·x

−i p

·x

(5)

hold.

Solution. (a) A partial integration of the time integral yields

∞

−∞

dt e

i p

·x

∂

−i p

·x



i( p

−p

)·x



t=+∞

t=−∞

−

+∞

−∞

dtA

−i p

·x

∂

i p

·x

=−i( p

)

+∞

−∞

dt e

i p

·x

−i p

·x

. (6)

The surface term vanishes because of the boundary condition (2a).

(b) Analogously, a partial integration over the spacial coordinates leads to

(Gauss’s theorem)

x e

i p

·x

∇ ·



−i p

·x



surface, |x|→∞

dF · A e

i( p

−p

)·x

−

x e

−i p

·x

A·∇ e

i p

·x

= i p

x e

i p

·x

A e

−i p

·x

. (7)

32 2. Review of Relativistic Field Theory

Exercise 2.1

Owing to boundary condition (2b), the surface integral again vanishes.

x e

i p

·x

∂



−i p

·x



=−i( p

)

x e

i p

·x

−i p

·x

. (8)

On the other hand we have

∂

−i p

·x

=−i( p

)

−i p

·x

, (9)

i.e.,

x e

i p

·x



∂

+ A

∂



−i p

·x

=−i( p

+ p

)

x e

i p

·x

−i p

·x

. (10)

2.2.3 π

Scattering

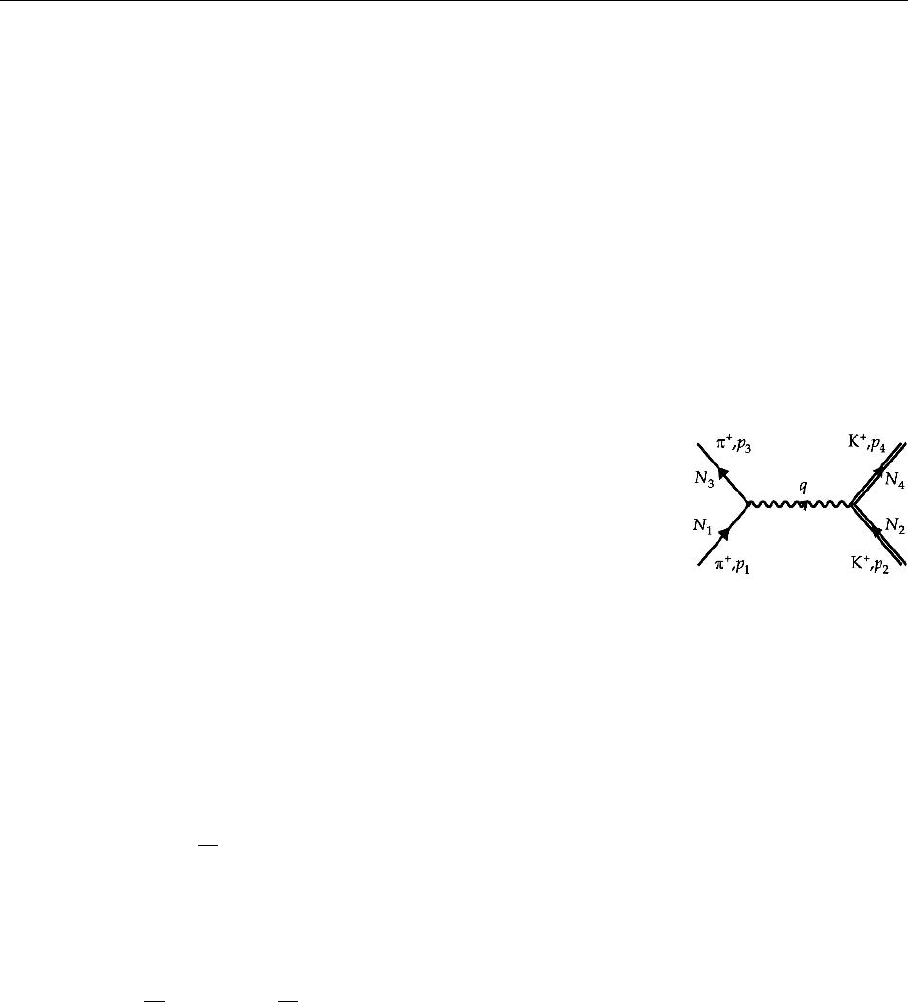
As a further example we now consider π

scattering and again evaluate the

transition matrix element S

(1)

. Being a spin-0 particle, the K

meson obeys

the same wave equation as the pion. Since π

and K

are distinguishable parti-

cles, they need not be symmetrized and exchange amplitudes do not have to be

taken into accout. The scattering reaction can be described in the following man-

ner. The electric charge of the K

creates a vector potential by which the π

scattered. First we have to determine this vector potential, because it enters the

scattering amplitude (2.83).

obeys Maxwell’s equations

A

−∂

(∂

) = j

. (2.92)

Here j

denotes an electromagnetic current density, which will be further

speciﬁed later. It is well known that (2.92) can be simpliﬁed by choosing

a speciﬁc gauge. One should remember that (2.92) remains invariant under gauge

transformations of the form

= A



−∂

Λ, (2.93)

with an arbitrary scalar function Λ(x), i.e., A



obeys the same equations (2.92)

as A

. One can therefore always choose the gauge Λ(x) in such a way that

∂

= 0 (2.94)

We use here the Heaviside-Lorentz units of electrodynamics, in contrast to Gauß units,

which are used in W. Greiner and J. Reinhardt: Quantum Electrodynamics,3rded.

(Springer, Berlin, Heidelberg, 2003). See in particular Section 4.2 and Exercise 4.2 of

this volume, where various gauges and unit systems are discussed.

2.2 Scalar Quantum Electrodynamics 33

holds. Equation (2.94) is referred to as the Lorentz condition. By requiring con-

dition (2.94) we have ﬁxed a certain gauge and are now able to determine A

.In

this Lorentz gauge the Maxwell equations reduce to

A

= j

. (2.95)

In order to derive the vector potential A

of K

mesons, the K

transition

current has to be speciﬁed and inserted into the right-hand side of (2.95). As

already mentioned the K

is a Klein–Gordon particle just like the π

and we

can therefore construct j

) in complete analogy to the pion current (2.90)

or (2.91):

) = ie



∗

(∂

) −(∂

∗

)ϕ



=eN

( p

+ p

)

i( p

−p

)·x

. (2.96)

The notation is explained in Fig. 2.7, which represents π

scattering to low-

est order. The formal solutions of (2.95) corresponding to the K

transition

current (2.96) are

=

−1

), (2.97)

where the inverse quabla operator is deﬁned by



−1

 = 11 . (2.98a)



−1

can be identiﬁed by its action on a plane wave:



−1



e

−iq·x





−1



−q

−iq·x



−iq·x

, (2.98b)



−1

−iq·x

=−

−iq·x

. (2.98c)

Now the four-potential (2.97), which is created by the transition current (2.96),

is readily obtained:

) =−

( p

+ p

)

iq·x

. (2.99)

Here the transferred four-momentum is

=( p

− p

)

=( p

− p

)

. (2.100)

Fig. 2.7. A Feynman dia-

gram for π

scattering

to lowest order (one-photon

exchange). The normaliza-

tion factors are also shown

34 2. Review of Relativistic Field Theory

Inserting this result into the scattering amplitude of (2.89) leads to

(1)

(π

) =−i

(π

)

= i

(π

)

= ie

( p

+ p

)

( p

+ p

)

x e

i( p

−p

)·x

i( p

−p

)·x

=−iN

(2π)

( p

+ p

− p

)

×e( p

+ p

)



−

µν



e(p

+ p

)

=−iN

(2π)

( p

+ p

− p

. (2.101)

The last step includes the deﬁnition of the reduced scattering amplitude F

which is mainly given by the current–current coupling connected with the photon

propagator. Now we can interpret the factors occurring in this result (2.101):

1. Every external line in a Feynman graph yields a normalization factor N

2. The mesons interact via exchange of a virtual photon, which is represented

in the graph by a wavy line. This line corresponds to the photon propagator

µν

(q) = g

µν

D(q

) =−

µν

(2.102)

in (2.101). The last step of (2.102) shows how the photon propagator is repre-

sented in graphs (diagrams). The square of the momentum transfer q

is often

referred to as the squared mass of the virtual photon. This is completely analo-

gous to q

, which holds for every four-momentum of a particle with rest

mass m

. A free photon obeys the homogeneous Maxwell equations

A

= 0 . (2.103)

This equation is only solved by a plane wave of the form exp(−iqx) if

=0 (2.104)

holds. But this condition shows that real photons are massless (m

=0). Virtual

photons, however, which are exchanged by electromagnetically interacting par-

ticles, are characterized by q

= 0 and referred to as off mass shell. We should

emphasize that the form (2.102) of the photon propagator is only valid within the

Lorentz gauge. It is deﬁned by

D

µν

(x −x



) =−g

µν

(x −x



) (2.105)

the form of the photon propagator in different gauges. One remark is already here

appropriate: The factor i in front of the ﬁnal expression for the matrix element

2.2 Scalar Quantum Electrodynamics 35

in equation (2.101) will from now on be attached to the photon propagator,

i. e., wherever D

µν

occurs, it will be replaced by iD

µν

. This is in accordance

with the general Feynman rules, which are discussed in great detail in Quantum

Electrodynamics.

3. There are two vertices in the graph for π

scattering. Since the virtual

photon propagator D

µν

is a tensor with respect to Lorentz indices, there must be

four-vectors on the left- and the right-hand sides, in order to produce a scalar.

In the case of spinless mesons, however, there is only one characterizing four-

vector, which is the four-momentum. This fact and the symmetry of the initial

and ﬁnal lines at the vertex explain the factors e(p

+ p

) and e(p

+ p

) in

(2.101). The tensor character of the photon propagator is due to the photon being

a spin-1 particle.

4. The transition currents in momentum space (vertices) as well as the photon

propagator have been deﬁned with factors ±i in a way that yields the correct sign

also at higher orders. The main advantage of this convention is that scattering

amplitudes for arbitrary graphs can immediately be constructed.

5. The four-momenta of the incoming and outgoing particles (the external lines

in the graph) are subject to four-momentum conservation, which is taken into

account by the factor (2π)

( p

+ p

− p

2.2.4 The Cross Section

We have already mentioned that plane waves (2.68) with probability density

(2.71a) are not normalized as usual to one particle per volume V but rather to

particles per volume V , i.e.,



, (2.106)

where we have made use of (2.74) once again. This makes sense because both

 and E are the zero components of four-vectors. We have already become ac-

quainted with the covariant normalization of Dirac spinors and its advantages in

describing meson–meson scattering processes. Of course, one has to choose ﬂux

and phase-space factors correspondingly, since the cross section must not depend

on the normalization scheme. Here we employ the normalization

x 

= 2E

, (2.107)

which leads to N

= 1/

√

V . The transition probability per unit volume and unit

time is given by

/VT . (2.108)

see W. Greiner and J. Reinhardt: Quantum Electrodynamics, 3rd ed. (Springer, Berlin,

Heidelberg, 2003).