Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

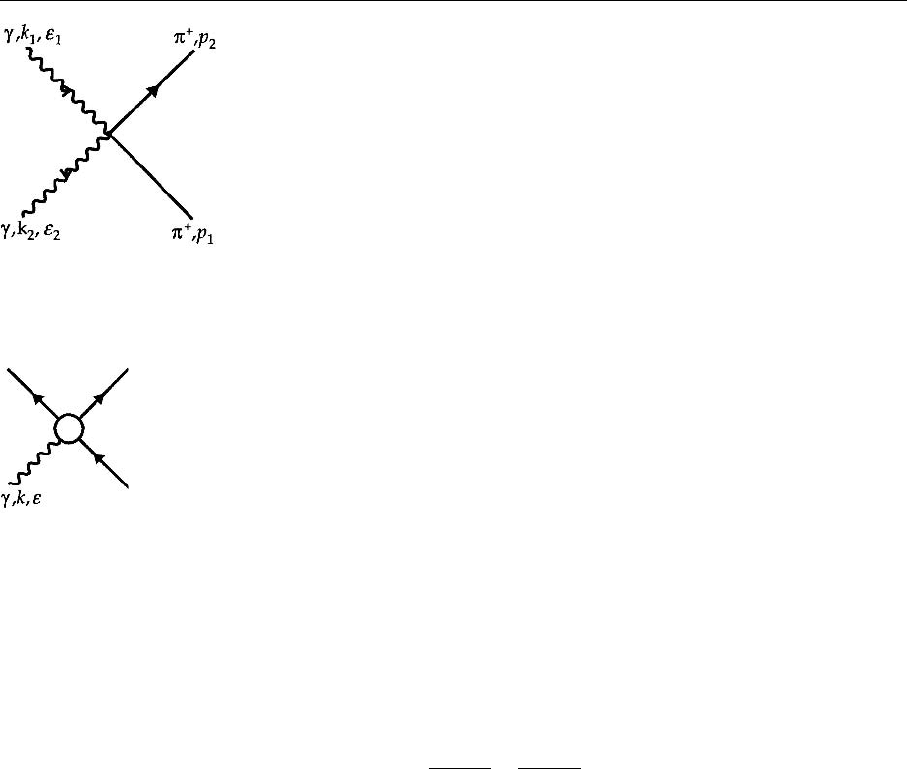
56 2. Review of Relativistic Field Theory
Fig. 2.17. The four-point
contact graph for γ π
+
→
γ π
+
Fig. 2.18. The graph of a
general one-photon process
This interaction will directly lead to graphs of the form shown in Fig. 2.17, i.e.,
to vertices with two photon lines. Such contributions are called contact terms.
They can be interpreted using gauge invariance arguments. To this end we first
consider the process shown in Fig. 2.18, where the initial state consists of one
photon and one particle and the final state of two particles. One photon is ab-
sorbed and two particles are emitted in the final channel. Of course, one of the
outgoing particles can again be a photon, i.e., the Compton scattering treated
above is included in such a process. The corresponding amplitude (see Fig. 2.18)
must be linear in the polarization ε
µ
and can therefore be factorized into
A = ε
µ
T
µ
, (18)
where T
µ
contains all the details of the process. In the Lorentz gauge, the
condition
ε ·k = 0
must hold. As we have already discussed in Sect. 2.2.5 an additional gauge
transformation
ε
µ
= ε
µ
+βk
µ
may be performed without changing any physical results. This transformation
corresponds to an additional gauge transformation within the Lorentz gauge.
Since the amplitude (18) must be gauge invariant, we are lead to the condition
k
µ
T
µ
=0 . (19)
The total scattering amplitude for γπ
+
Compton scattering derived above can be
written as
F
γπ
= F
(d)
γπ
+F
(e)
γπ
= 4e
2
ε
µ
1
ε
ν∗
2
p
1µ
p
2ν
s −m
2
0
+
p
2µ
p
1ν
u −m
2
0
≡ ε
µ
1
ε
ν∗
2
T
µν
. (20)
According to the transition from (18) to (19) we have to replace ε
1
by k
1
and
evaluate
k
µ
1
ε
ν∗
2
T
µν
.
The scalar products that occur,
2p
1
·k
1
= s −m
2
0
, 2p
2
·k
1
=−(u −m
2
0
), (21)
then give
k
µ
1
ε
ν∗
2
T
µν
= 2e
2
ε
ν∗
2
( p
2
− p
1
)
ν
= 2e
2
ε
∗
2
·k
1
= 0 . (22)

2.2 Scalar Quantum Electrodynamics 57
This result is surprising, because the total scattering amplitude (20) derived so far
explicitly violates condition (19). If we also replace ε
2
by k
2
in (22), we obtain
k
µ
1
k
ν
2
T
µν
= 2e
2
k
1
·k
2
= 0 . (23)
Again this result is not equal to zero. The only possible explanation for this ob-
servation is that the amplitude (20) is not gauge invariant. But where did we make
a mistake? We wanted to evaluate a process of second order in e,butsofarwe
have not taken into account the contact graphs according to the interaction (17),
which are of the same order. In order to restore gauge invariance and fulfill condi-
tions (19), T
µ
(or T
µν
in (20)) must contain all the interactions of a given order.
If the coupling constant e is interpreted as a variable quantity (which then as-
sumes some fixed value), gauge invariance must separately be fulfilled in every
order in e. We therefore expect an additional term F
(c)
γπ
for the complete Compton
scattering amplitude, i.e.,
F
γπ
= F
(d)
γπ
+F
(e)
γπ
+F
(c)
γπ
, (24)
where the superscripts (d), (e) and (c) denote the direct, exchange and contact
term, respectively. Also F
(c)
γπ
must be linear in ε
1
and ε
∗
2
and by means of the
replacements
ε
1
→k
1
,ε
∗
2
→k
2
(25)
it must yield (22) or (23) with the opposite sign. Only in this way can the gauge
invariance of the scattering amplitude (24) be ensured. Apparently,
F
(c)
γπ
=−2e
2
ε
1
·ε
∗
2
(26)
must hold. This scattering amplitude is caused by the quadratic interaction. One
must understand that if we had in general ignored the interaction −e
2
A
2
, gauge
invariance in second order would have demanded its existence. This is a first ex-
ample of the power of gauge symmetry. A further comment on equation (26) is
appropriate: this term is the only one that is linear in ε
1
and ε
∗
2
anduptoasign
equal to (22) and (23). There are no other terms fulfilling these equations! The
expression (26) for the so-called seagull graph has been explicitly derived in
chapter 8 of reference
4
— see equations (8.31) ff.
Taking into account (20), (24), and (26), we get for the total invariant
scattering amplitude for Compton scattering by a pion
F
γπ
=e
2
ε
µ
1
ε
ν∗
2
4p
1µ
p
2ν
s −m
2
0
+
4p
2µ
p
1ν
u −m
2
0
−2g
µν
. (27)
The factor 2 in front of the g
µν
term is plausible, because each factor A
µ
in A
2
of equation (17) can represent one absorption and one emission process. Mul-
tiplying (27) by the four-momentum conservation (2π)
4
δ
4
( p
2
+k
2
− p
1
−k
1
)
and normalization factors then yields the complete Compton S-matrix element.
Example 2.8
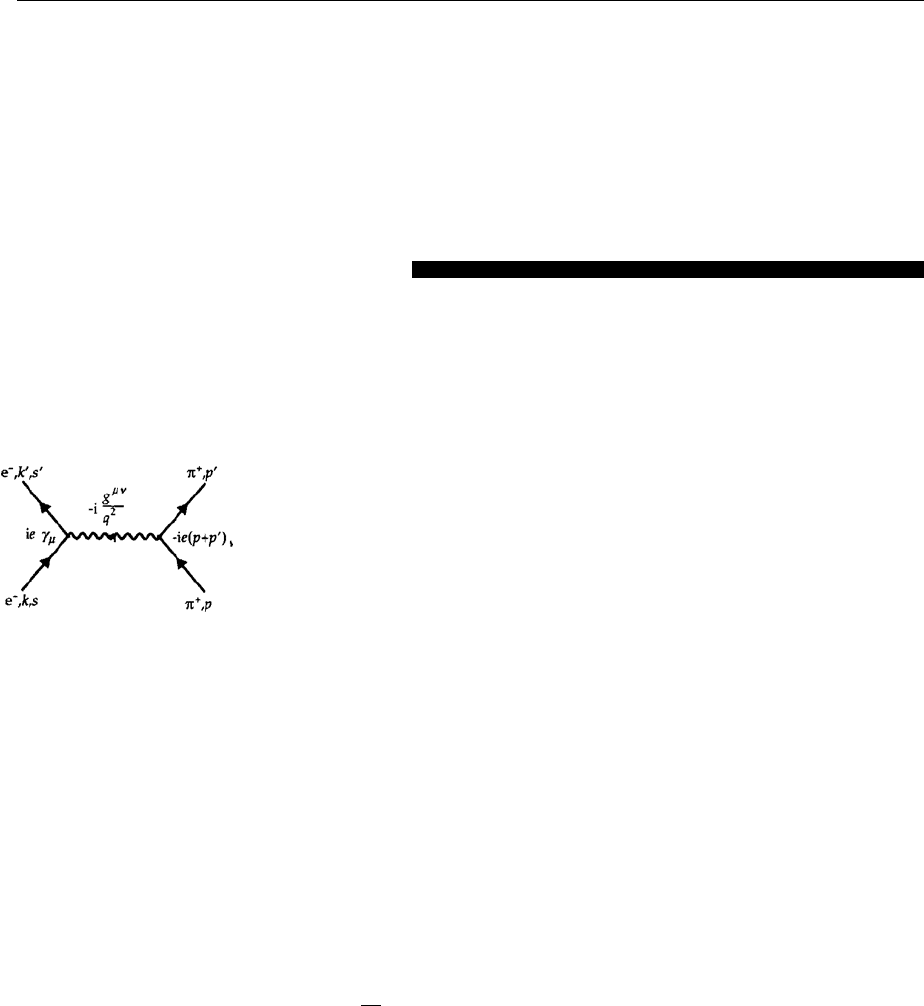
58 2. Review of Relativistic Field Theory
Fig. 2.19. The Feynman dia-
gram for e
−
π
+
scattering in
the one-photon exchange ap-
proximation
2.3 Fermion–Boson and Fermion–Fermion Scattering
In this section we discuss a number of problems and examples to review and
deepen our knowledge of QED. We shall encounter well-known subjects in new
forms and also gain new insights. Our notation will get closer to that employed
in high-energy physics.
EXERCISE
2.9 Elastic e
−
π
+
Scattering (I)
Problem. Determine the scattering amplitude and explain the formal steps
necessary to evaluate the cross section.
Solution. The graph for e
−
π
+
scattering is of the following form (see Fig. 2.19).
Most of the above notation is readily understood. Only the factor +iinthetran-
sition current at the electron vertex, which has been denoted by (ieγ
µ
), needs
additional explanation. Reviewing our knowledge of QED, we start with the
scattering amplitude (2.58), i.e., with
S
(1)
fi
=−i
d
4
xj
µ
(e
−
)A
µ
, (1)
where according to (2.60)
j
µ
(e
−
) = (−e)NN
¯
u(k
, s
)γ
µ
u(k, s) e
i(k
−k)·x
(2)
denotes the electron transition current density. The electromagnetic four-
potential A
µ
in (1) is created by the pion (π
+
) transition current density
j
µ
(π
+
) = (+e)
¯
N
¯
N
( p + p
)
µ
e
i( p
−p)·x
. (3)
According to (2.99) we have
A
µ
=−
1
q
2
j
µ
(π
+
), (4)
with the four-momentum transfer
q = p
− p = k −k
. (5)

2.3 Fermion–Boson and Fermion–Fermion Scattering 59
The scattering amplitude (1) in detail is then
S
(1)
fi
=−i
d
4
xj
µ
(e
−
)
−
1
q
2
j
µ
(π
+
)
=iNN
¯
N
¯
N
d
4
x
¯
u(k
, s
)γ
µ
u(k, s) e
i(k
−k)·x
×
−
e
2
q
2
( p + p
)
µ
e
i( p
−p)·x
=−iNN
¯
N
¯
N
(2π)
4
δ
4
(k
+ p
−k − p)(−e)
¯
u(k
, s
)γ
µ
u(k, s)
×
−
g
µν
q
2
(+e)(p + p
)
ν
=−iNN
¯
N
¯
N
(2π)
4
δ
4
( p
+k
− p −k)F
ss
(kp;k
p
). (6)
Inthelaststepwehaveintroducedtheinvariant scattering amplitude
F
ss
(kp;k
p
) = (−e)
¯
u(k
, s
)γ
µ
u(k, s)
−
g
µν
q
2
(+e)
( p + p
)
ν
. (7)
Only the spin variables occur in addition. Now we see from (6) that the above
Feynman rules yield the correct total sign for the scattering amplitude if a factor
+i is assigned to the vertex of the leptonic transition current. Figure 2.19 already
contains this factor. Note that the spinor combinations (
uγ
µ
u) are the compo-
nents of a four-vector. Contracting this vector with (p + p
)
ν
yields a Lorentz
scalar and therefore a Lorentz-invariant scattering amplitude. The derivation of
the cross section consists in the same steps, which have been discussed in detail
for π
+
K
+
scattering. Employing the four-vectors
k
µ
= (ω, k), k
µ
=(ω
, k
),
p
µ
= (E, p), p
µ
= (E
, p
), (8)
we find the differential cross section to be (see equation (2.116))
dσ
ss
= (2π)
4
δ(k
+ p
−k − p)
|F
ss
|
2
2E2ω|v|
1
(2π)
3
d
3
k
2ω
1
(2π)
3
d
3
p
2E
. (9)
The scattering amplitude F
ss
can be easily evaluated if we insert the spinors (see
(2.41))
u(k, s) =
√
w +m
0
φ
s
ˆ
σ·k
ω+m
0
φ
s
(10)
into (7). This procedure is quite tedious and, more importantly, does not yield the
quantity observed in most of the actual experiments. The interesting quantity is
the so-called nonpolarized cross section, which is obtained from (9) by averaging
over the initial spins and summing over the final spins, i.e.,
d
¯
σ =
1
2
(dσ
↑↑
+dσ
↑↓
+dσ
↑↓
+dσ
↓↓
)
=
1
2
ss
dσ
ss
. (11)
Exercise 2.9

60 2. Review of Relativistic Field Theory
Exercise 2.9
These lengthy summations need not be performed explicitly. Instead, employ-
ing Feynman’s trace techniques enables us to drastically simplify the spin
summations (11).
2.3.1 Traces and Spin Summations
Let us briefly review the basic facts about trace techniques. The trace of a matrix
is the sum of its diagonal elements, i.e.,
tr{A}=
i
A
ii
. (2.154)
Cyclic permutability holds under the trace
tr{AB}=tr{BA} ,
tr{ABC}=tr{CAB}=tr{BC A} . (2.155)
The most important relations for traces over products of γ matrices and Feynman
“daggers” needed in this context are as follows. By using the anticommutation
relation
{γ
µ
,γ
ν
}=2g
µν
11
the following traces can be easily evaluated:
tr{
11}=4 ,
tr{γ
µ
γ
ν
}=4 g
µν
,
tr{a/b/}=4 a ·b ,
tr{a/b/c/d/}=4
(a ·b)(c ·d) +(a ·d)(b ·c) −(a ·c)(b ·d)
, (2.156)
where use has been made of the fact that
a/b/ =−b/a/ +2 a ·b (2.157)
holds (see Exercise 2.10). An expression for the scattering cross section in
lepton–pion scattering was derived in the Exercise 2.9. There the square of the
scattering amplitude F
ss
appears in the cross section:
|F
ss
|
2
=
e
2
q
2
2
¯
u(k
, s
)γ
µ
u(k, s)
[p + p
]
µ
×
¯
u(k
, s
)γ
ν
u(k, s)
[p + p
]
ν
∗
. (2.158)
2.3 Fermion–Boson and Fermion–Fermion Scattering 61
Since F
ss
is a complex number (all matrix indices are summed over), we can
replace the conjugate term {...}
∗
by the Hermitian conjugate; we find that
¯
u(k
, s
)γ
ν
u(k, s)
[p + p
]
ν
†
=
u
†
(k, s)γ
†
ν
γ
0
u(k
, s
)
[p + p
]
ν
=
¯
u(k, s)γ
ν
u(k
, s
)
[p + p
]
ν
, (2.159)
since
γ
0
γ
†
ν
γ
0
=γ
ν
,γ
†
0
=γ
0
(2.160)
holds. The four-vector ( p + p
)
ν
has real components and is therefore not
changed by the operations (...)
∗
and (...)
†
. In performing the spin summation
according to (11) in Exercise 2.9 we must calculate the following expression:
1
2
s,s
|F
ss
|
2
=
1
2
e
2
q
2
2
s,s
¯
u(k
, s
)γ
µ
u(k, s)
×
¯
u(k, s)γ
ν
u(k
, s
)
( p + p
)
µ
( p + p
)
ν
≡
e
2
q
2
2
L
µν
T
µν
, (2.161)
wherewehaveintroducedtheso-calledlepton tensor
L
µν
=
1
2
s,s
¯
u(k
, s
)γ
µ
u(k, s)
¯
u(k, s)γ
ν
u(k
, s
) (2.162)
and the so-called hadron tensor
T
µν
= ( p + p
)
µ
( p + p
)
ν
. (2.163)
The factorization of the scattering cross section into a leptonic and a hadronic
part stems from the one-photon approximation. To higher order, the situation is
more complicated. The middle term (the direct product of two spinors)
s
u(k, s) ⊗
¯
u(k, s)
βγ
=
s
u
β
(k, s)
¯
u
γ
(k, s), (2.164)
which no longer depends on s (s is summed over), is a 4×4 matrix. Making use
of the explicit form u(k, s) of the spinor and the fact that for two-component
spinors φ
s
s
φ
s
φ
s†
= φ
1
φ
1†
+φ
2
φ
2†
=
1
0
(1, 0) +
0
1
(0, 1)
=
10
00
+
00
01
=
11 (2.165)

62 2. Review of Relativistic Field Theory
holds, we can deduce that
s
u(k, s)
¯
u(k, s) =u(k, ↑)
¯
u(k, ↑) +u(k, ↓)
¯
u(k, ↓)
=(ω +m
0
)
11 −
ˆ
σ·k
ω+m
0
ˆ
σ·k
ω+m
0
−
ω−m
0
ω+m
0
11
=(k/ +m
0
). (2.166)
In Exercise 2.10, we shall perform this calculation in detail. Using this result,
(2.164) can be expressed by (2.166) and inserted into (2.162), which leads to
L
µν
=
1
2
s
α,β,γ,δ
¯
u
α
(k
, s
)(γ
µ
)
αβ
(k/ +m
0
)
βγ
(γ
ν
)
γδ
u
δ
(k
, s
), (2.167)
written in expanded matrix notation. Each single factor in this term represents
a c-number, and the factors can therefore be reordered arbitrarily. In particular,
the sum
s
u
δ
(k
, s
)
¯
u
α
(k
, s
) = (k/
+m
0
)
δα
(2.168)
can be performed using (2.166), and the lepton tensor is thus reduced to the form
L
µν
=
1
2
α,β,γ,δ
(k/
+m
0
)
δα
(γ
µ
)
αβ
(k/ +m
0
)
βγ
(γ
ν
)
γδ
=
1
2
tr{(k/
+m
0
)γ
µ
(k/ +m
0
)γ
ν
} . (2.169)
Using the trace formulas from (2.156) we obtain
tr{(k/
+m
0
)γ
µ
(k/ +m
0
)γ
ν
}=tr{k/
γ
µ
k/γ
ν
}+m
2
0
tr{γ
µ
γ
ν
}
=4(k
µ
k
ν
+k
ν
k
µ
−k ·k
g
µν
) +4m
2
0
g
µν
. (2.170)
If we take into account that the mass squared is
q
2
=(k −k
)
2
= k
2
+k
2
−2k ·k
= 2(m
2
0
−k ·k
), (2.171)
this can be inserted into (2.170), and the lepton tensor can finally be written as
L
µν
= 2
k
µ
k
ν
+k
ν
k
µ
+
1
2
q
2
g
µν
. (2.172)
This tensor not only is important for elastic scattering, but also plays a major role
in most quark–parton calculations. We shall perform the contraction of L
µν
with
the hadron tensor T
µν
in the pion rest system ( p
µ
= (M
,
0)) according to (2.161)
in Exercise 2.11 to calculate the cross section. Neglecting the electron mass (the

2.3 Fermion–Boson and Fermion–Fermion Scattering 63
ultrarelativistic limit), the result is
d
¯
σ
dΩ
=
α
2
4k
2
sin
4
(θ/2)
k
k
cos
2
θ
2
=
α
2
4ω
2
sin
4
(θ/2)
ω
ω
cos
2
θ
2
, (2.173)
where
k =|k|=ω,
k
=|k
|=ω
, (2.174)
and
q
2
=−4 kk
sin
2
θ
2
. (2.175)
θ is the scattering angle of the electron (see Fig. 2.20).
The preceding considerations that culminate in the scattering cross section
(2.173) are based on treating pions and electrons as pointlike. We thus label the
cross section “n.s.” (meaning “no structure”):
d
¯
σ
dΩ
n.s.
(2.176)
Today it is accepted that pions have an internal structure, being composed of
quarks, antiquarks, and gluons. Leptons, on the other hand, are still considered to
be elementary, i.e., without internal structure. This conclusion is drawn mainly
from lepton–lepton scattering.
EXERCISE
2.10 Features of Dirac Matrices
Problem. Start with the anticommutator
$
γ
µ
,γ
ν
%
=2g
µν
11(1)
and show that the following relations hold:
(a) a/b/ =−b/a/ +2a ·b . (2)
(b) (k/ −m
0
)(k/ +m
0
) = (k/ +m
0
)(k/ −m
0
)
= 0 , for k
2
=m
2
0
. (3)
Fig. 2.20. The definition of
the e
−
scattering angle in
e
−
π
+
scattering
64 2. Review of Relativistic Field Theory
Exercise 2.10
(c)
ˆ
Λ
+
(k) = (k/ +m
0
), (4)
which eliminates the negative energy parts of an arbitrary spinor, and
ˆ
Λ
−
(k) = (k/ −m
0
), (5)
which eliminates the positive energy parts of an arbitrary spinor.
(d) Employ the explicit forms
u(k, s) =
√
ω +m
0
φ
s
ˆ
σ·k
ω+m
0
φ
s
,
φ
1
=
1
0
,φ
2
=
0
1
, (6)
v(k, s) =
√
ω +m
0
ˆ
σ·k
ω+m
0
χ
s
χ
s
,
χ
1
=
0
1
,χ
2
=
1
0
(7)
and show how the 4×4 matrices
s
u(k, s)u(k, s) and
s
v(k, s)v(k, s) depend
on
ˆ
Λ
+
(k) and
ˆ
Λ
−
(k), respectively.
Solution.
(a) a/b/ +b/a/ = a
µ
γ
µ
b
ν
γ
ν
+b
ν
γ
ν
a
µ
γ
µ
=a
µ
b
ν
$
γ
µ
,γ
ν
%
= 2a
µ
b
ν
g
µν
11 =2a ·b11 ; (8)
from this equation follows in particular that a/
2
=a
2
11.
(b)
(
k/ −m
0
11
)(
k/ +m
0
11
)
=
k/
2
−m
2
0
11
=
k
2
−m
2
0
11 =0 . (9)
(c) The wave function of a particle with positive energy and four-momentum k
µ
can be written as
Ψ
(+)
(x) =
s
b
s
u(k, s) e
−ik·x
. (10)
Correspondingly a solution with negative energy and four-momentum k
−µ
is
Ψ
(−)
(x) =
s
d
s
v(k, s) e
ik·x
. (11)
Both wave functions must obey the Dirac equation, i.e.,
(
i∇/ −m
0
)
Ψ
(+)
(x) =
(
k/ −m
0
)
Ψ
(+)
(x)
=
ˆ
Λ
−(k)
Ψ
(+)
(x) = 0 (12)
2.3 Fermion–Boson and Fermion–Fermion Scattering 65
and
(
i∇/ −m
0
)
Ψ
(−)
(x) =−
(
k/ +m
0
)
Ψ
(−)
(x)
=−
ˆ
Λ
+(k)
Ψ
(−)
(x) = 0 . (13)
Equations (12) and (13) can also be put into the form
k/Ψ
(+)
(x) = m
0
Ψ
(+)
(x),
k/Ψ
(−)
(x) =−m
0
Ψ
(−)
(x). (14)
From (14) we immediately obtain
ˆ
Λ
+
Ψ =2m
0
Ψ
(+)
,
ˆ
Λ
−
Ψ =−2m
0
Ψ
(−)
. (15)
(d)
s
u(k, s)
¯
u(k, s) =
s
u(k, s)u
†
(k, s)γ
0
=(ω +m
0
)
s
φ
s
ˆ
σ·k
ω+m
0
φ
s
φ
s†
,φ
s†
ˆ
σ
†
·k
ω +m
0
110
0 −11
=(ω +m
0
)
s
φ
s
φ
s†
−φ
s
φ
s†
ˆ
σ
†
·k
ω+m
0
ˆ
σ·k
ω+m
0
φ
s
φ
s†
−
ˆ
σ·k
ω+m
0
φ
s
φ
s†
ˆ
σ
†
·k
ω+m
0
. (16)
Now we employ the Hermiticity of the Pauli matrices,
ˆ
σ
†
=
ˆ
σ,andmakeuseof
the identity
s
φ
s
φ
s†
=11 (cf. (2.165)). Equation (16) then assumes the form
(
ω +m
0
)
⎛
⎝
11 −
ˆ
σ·k
ω+m
0
ˆ
σ·k
ω+m
0
−
(
ˆ
σ·k)
2
(ω+m
0
)
2
⎞
⎠
. (17)
But since we have
ˆ
σ ·k
2
=
1
2
k
i
k
j
ˆ
σ
i
ˆ
σ
j
+
ˆ
σ
j
ˆ
σ
i
= k
i
k
j
δ
ij
= k
2
=ω
2
−m
2
0
,
the result becomes
(ω +m
0
)11 −
ˆ
σ ·k
ˆ
σ ·k (−ω +m
0
)11
. (18)
Employing the γ -matrix representation
γ
0
=
110
0 −11
, γ =
0 σ
−σ 0
, (19)
Exercise 2.10
