Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

66 2. Review of Relativistic Field Theory
Exercise 2.10
we obtain the result
s
u(k, s)
¯
u(k, s) =ωγ
0
−k ·γ +m
0
=
(
k/ +m
0
)
=
ˆ
Λ
+
(k).
An analogous calculation for negative solutions yields
s
v(k, s)
¯
v(k, s)
= (ω +m
0
)
s
ˆ
σ·k
ω+m
0
χ
s
χ
s
χ
s†
ˆ
σ ·k
ω +m
0
, −χ
s
= (ω +m
0
)
ω
2
−m
2
0
(ω+m
0
)
2
−
ˆ
σ·k
ω+m
0
ˆ
σ·k
ω+m
0
−11
=
(ω −m
0
)11 −
ˆ
σ ·k
ˆ
σ ·k (−ω −m
0
)11
= ωγ
0
−k ·γ −m
0
= (k/ −m
0
) =−
ˆ
Λ
−
(k). (20)
EXERCISE
2.11 Electron–Pion Scattering (II)
Problem. Evaluate in detail the nonpolarized π
+
e
−
cross section. Start with the
expressions given in (2.116) and (2.120) and use
d
¯
σ =
1
4Eω|v|
1
2
s,s
|F
ss
|
2
dLips(s;k
p
).
Determine d
σ/dΩ in the rest system of the pion ( p
µ
=(M, 0)).
Solution. We denote the four-momenta of the pion before and after the collision
by p
µ
=(M, 0) and p
µ
=(E
, p
), respectively. k
µ
= (ω, k) and k
µ
= (ω
, k
)
are the corresponding four-momenta of the incoming and outgoing electrons.
The scattering angle θ is the angle between the directions k and k
and q = k
−k
denotes the momentum transfer. In the following we only consider high elec-
tron energies, i.e., since ω, ω
m, the electron rest mass can be neglected.
Therefore we have ω =|k| and ω
=|k
| and the invariant flux factor is simply
4
(k · p)
2
−m
2
M
2
4Mω. (1)
2.3 Fermion–Boson and Fermion–Fermion Scattering 67
According to the Feynman rules the spin average of the squared scattering ampli-
tude describing the exchange of one photon is given by the contraction of lepton
and hadron tensor:
1
2
s,s
|F
ss
|
2
=
4πα
q
2
2
L
µν
T
µν
. (2)
Employing (2.163) and (2.172) we obtain
L
µν
T
µν
= 8
2(k · p)(k
· p) +
q
2
2M
2
. (3)
In the ultrarelativistic limit, q
2
becomes
q
2
= (k −k
)
2
= (ω −ω
)
2
−(k −k
)
2
≈−2ωω
(1 −cos θ) =−4ωω
sin
2
θ
2
.
Hence
4πα
q
2
2
=
πα
ωω
2
1
sin
4
θ
2
(4)
and
L
µν
T
µν
= 16M
2
ωω
cos
2
θ
2
. (5)
Now we have to evaluate the invariant phase-space factor:
dLips(s;k
p
) = (2π)
4
δ
4
(k
+ p
−k − p)
1
(2π)
3
d
3
p
2E
1
(2π)
3
d
3
k
2ω
=
1
(4π)
2
δ
3
(k
+ p
−k)δ(E
−M +ω
−ω)
d
3
p
E
d
3
k
ω
. (6)
In order to evaluate the cross section for the electron to be scattered into a given
final state, we have to integrate over all final states of the pion. This is readily
achieved by means of the δ
3
function in (6) (owing to momentum conservation
only one final pion state is possible for a given final state of the electron). In the
remaining integrand p
must then be replaced by k −k
=−q. Because of the
identity
E
=
M
2
+ p
2
=
M
2
+q
2
=
"
M
2
+ω
2
+ω
2
−2ωω
cos θ (7)
E
is not an independent quantity either. Except for this factor there are no further
dependences of the integrand on p
, including the scattering amplitude and flux
factor. Finally ω
=|k
| leads to
d
3
k
ω
= ω
dω
dΩ, (8)
Exercise 2.11
68 2. Review of Relativistic Field Theory
Exercise 2.11
where dΩ denotes the spherical angle into which the electron is scattered. The
ω
integration is performed by using the remaining energy δ function, i.e., for
a given scattering angle the absolute value of the electron momentum is fixed by
kinematic arguments. Note that in the argument of the δ function E
depends on
ω
as well (cf. (7)). Therefore we have to employ the relation
δ
(
f(x)
)
=
i
δ(x −x
i
)
f
(x)|
x=x
i
, (9)
where the x
i
denote the zeros of the function f(x).Accordingto(7)wehave
d(E
−M +ω
−ω)
dω
=
ω
−ω cos θ +E
E
. (10)
Inserting now (7) into the identity E
= M +ω −ω
, which has been derived by
integrating over the δ function, we obtain
M(ω −ω
) = ωω
(1 −cos θ) , (11)
and inserting E
= M +ω −ω
into the right-hand side of (10) yields
d
dω
(E
−M +ω
−ω) =
ω(1 −cos θ) +M
E
, (12)
Combining equations (11) and (12), we obtain
d
dω
(E
+ω
) =
Mω
E
ω
. (13)
The (partially integrated) Lorentz-invariant phase-space factor now assumes the
form
dLips =
1
(4π)
2
ω
2
Mω
dΩ, (14)
where ω
is fixed by (11). Summarizing equations (1), (4), (5), and (14) finally
yields the nonpolarized cross section
d
¯
σ
dΩ
n.s.
=
α
2
4ω
2
sin
4
θ
2
ω
ω
cos
2
θ
2
. (15)
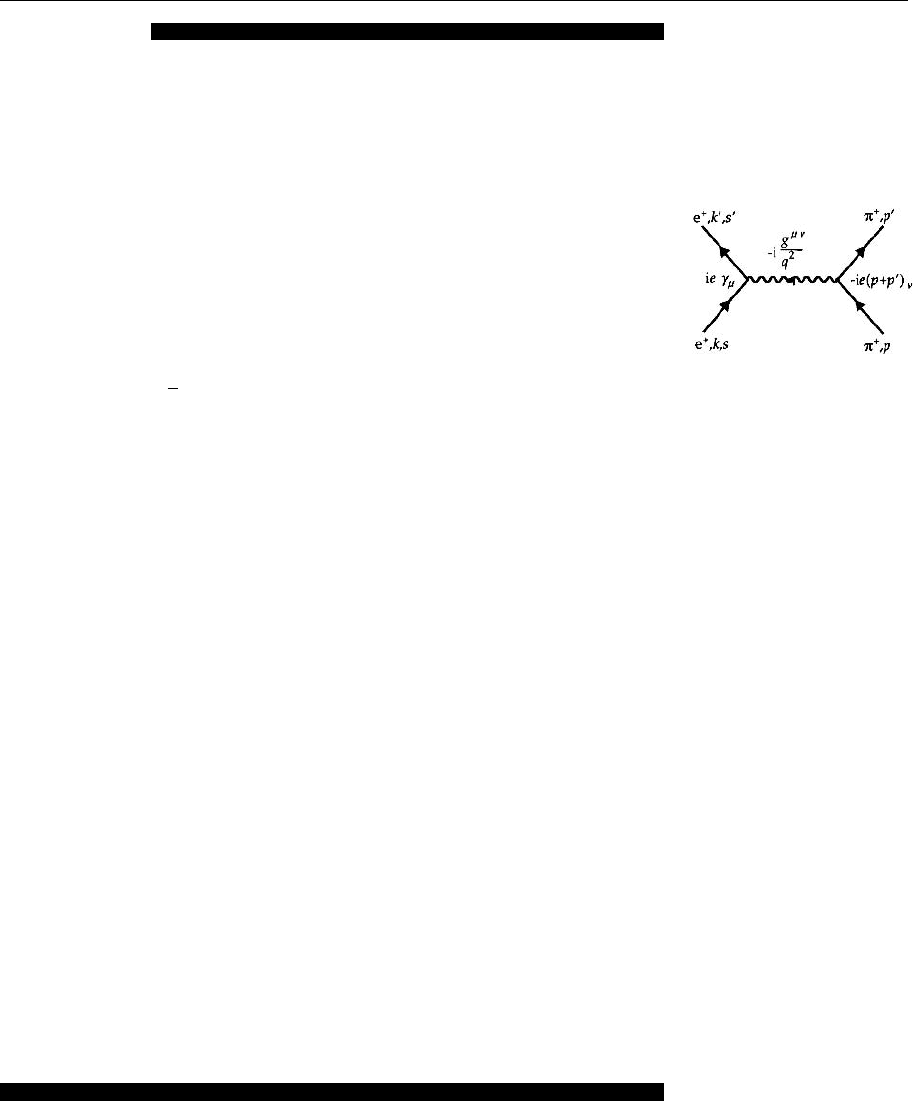
2.3 Fermion–Boson and Fermion–Fermion Scattering 69
EXERCISE
2.12 Positron–Pion Scattering
Problem. Show that the cross section for e
+
π
+
scattering is, in the one-photon-
exchange approximation, equal to that for e
−
π
+
scattering.
Solution. The graph for e
+
π
+
scattering is of the following form: The incoming
positron with four-momentum k and spin s is described as an outgoing electron
with four-momentum −k and spin −s. Correspondingly the outgoing positron
with k
, s
can be interpreted as an incoming electron with −k
, −s
. Therefore
we have for the positron transition current
j
µ
(e
+
) = (−e)NN
¯
v(k, s)γ
µ
v(k
, s
)e
−i(−k
+k)·x
, (1)
where v
k
, s
and
v
k
, s
represent an incoming electron wave −k
, −s
and
an outgoing electron wave −k, −s, respectively. If we construct the scattering
matrix element with j
µ
(e
+
), an additional minus sign is inserted according to
the previously introduced rules. Everything else remains the same as in the e
−
π
+
scattering discussed in Exercises 2.9 and 2.11. The evaluation of the cross sec-
tion, too, is analogous to that of e
−
π
+
scattering except for the spin average,
where the sum
s
u(k, s)
¯
u(k, s) = (k/ +m
0
) (2)
in the lepton tensor must be replaced by (see equations (2.164) and (20) of
Exercise 2.10)
s
v(k, s)
¯
v(k, s) =(k/ −m
0
). (3)
This calculation was made in Exercise 2.10 and leads to the trace
tr
$
(k/
−m
0
)γ
µ
(k/ −m
0
)γ
ν
%
(4)
instead of
tr
$
(k/
+m
0
)γ
µ
(k/ +m
0
)γ
ν
%
. (5)
Because of rules (2.156) we immediately recognize that these two traces are
equal. Therefore the e
+
π
+
cross section is to lowest order exactly equal to the
e
−
π
+
cross section. This result does not surprise us at all, since only the lep-
ton charge changed its sign and the lowest-order cross section contains only the
square of this charge.
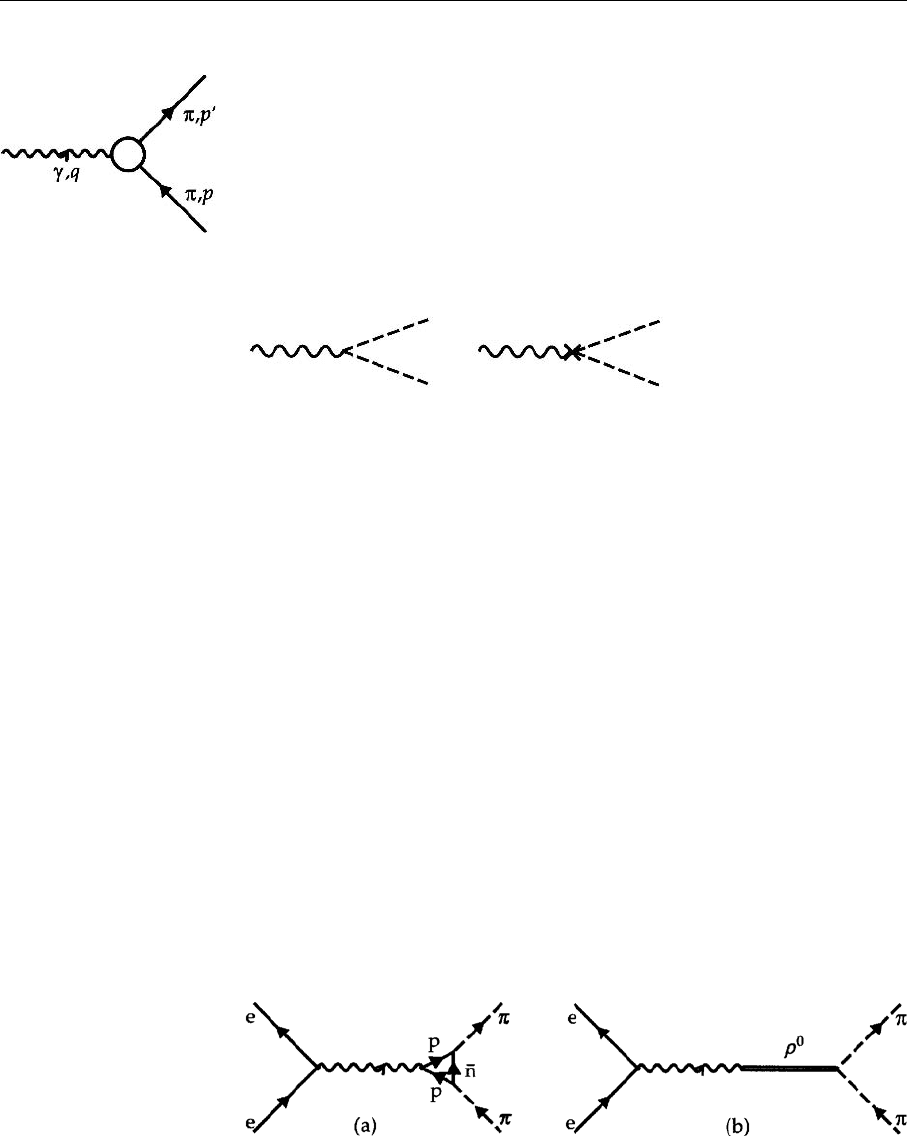
Fig. 2.21. e
+
π
+
scattering
in the one-photon- exchange
approximation
70 2. Review of Relativistic Field Theory
Fig. 2.22. The general pho-
ton–pion vertex. The circle
indicates the internal struc-
ture of the pion
Fig. 2.23a,b. Complex vir-
tual processes founded on
strong interactions and con-
tributing to the structure of
the γπ
+
vertex: (a) a virtual
nucleon loop; (b) a virtual
0
meson
2.3.2 The Structure of the F o rm Factors from Invariance Considerations
We now assume that the pion has an internal structure that we do not know
exactly but that can be parametrized in some rather general way, as we shall
demonstrate shortly. The photon–pion vertex with an internal pion structure is
drawn in Fig. 2.22. In place of some simple vertex, a circle is drawn, symboliz-
ing the internal strcuture of the pion, while a simple junction indicates the vertex
of a pointlike pion (without internal structure).
To exemplify which kind of processes can be contained in the circle, we men-
tion the two following graphs, drawn in the conventional framework without
imagining a quark structure of the pion.
Owing to the strong interaction (large coupling constant) such virtual pro-
cesses can contribute considerably to the total scattering amplitude. As we shall
see, even without detailed knowledge of the internal structure of the pion, gen-
eral statements about the form of the required modifications of the vertex can be
obtained from the Lorentz and gauge invariance of the theory. These two general
requirements fix the form of the scattering amplitude for any internal structure
imaginable.
For a pointlike pion, the transition amplitude is
j
µ
(π
+
) = eNN
( p + p
)
µ
e
i( p
−p)·x
. (2.177)
We now consider the current (2.177) as a matrix element of an electromagnetic
current operator (Heisenberg operator)
ˆ
j
µ
em
(x) (2.178)
and write
j
µ
(π
+
) =π
+
p
|
ˆ
j
µ
em
(x)|π
+
p . (2.179)
If (2.179) describes the special transition current of pointlike pions, we identify
π
+
p
|
ˆ
j
µ
em
(0)|π
+
p=eNN
( p + p
)
µ
. (2.180)

2.3 Fermion–Boson and Fermion–Fermion Scattering 71
Since the matrix element (2.179) is taken with plane pion waves, its x de-
pendence is given by the exponential factor in (2.177). This will also hold
unmodified for pions with internal structure, but we expect that the strong
interaction modifies the right-hand side of (2.180), i.e., the four-momentum
dependence:
π
+
p
|
ˆ
j
µ
em
(0)|π
+
p≡NN
Γ
µ
( p, p
, q), (2.181)
where the momentum transfer or four-momentum of the virtual photon q can also
enter.
Taking a rather pragmatic point of view, we simply try to parametrize the
four-current or Γ
µ
.AsΓ
µ
must remain a four-vector, we shall first discuss
which general four-vector Γ
µ
can be constructed from the available four-vectors
p, p
,andq. Owing to four-momentum conservation at the vertex
p
= p +q , (2.182)
only two independent four-vectors are available, which can be chosen to be
( p
+ p)
µ
and (p
− p)
µ
=q
µ
. (2.183)
Both can be utilized in the construction of Γ
µ
. Additionally, both four-vectors
(2.183) can be multiplied with an unknown scalar function. From the relations
p
2
= p
2
= M
2
,
p
2
= p
2
+2 p ·q +q
2
⇔ 2 p ·q =−q
2
, (2.184)
and
q
2
= 2M
2
−2 p · p
(2.185)
it can be seen that only one nontrivial scalar can be composed of the four-vectors
(2.183), namely p · p
or, equivalently, q
2
, the square of the momentum transfer
at the vertex. Using this, we can write the vertex function most generally using
Lorentz invariance as
Γ
µ
( p, p
, q) = e
F(q
2
)( p + p
)
µ
+G(q
2
)q
µ
. (2.186)
The scalar functions F(q
2
) and G(q
2
) are called form factors.
To discover what statements can be made about the form factors from gauge
invariance, we remember that the Maxwell equations are left invariant by the
gauge transformation A
µ
→ A
µ
= A
µ
−∂
µ
Λ. The Maxwell equations in the
Lorentz gauge are
A
µ
=A
µ
= j
µ
em
,∂
µ
A
µ
=0 . (2.187)
Since the current is not affected by the gauge transformation, only those Λ
satisfying
Λ = 0 can be considered. This gauge condition implies current
conservation:
∂
µ
j
µ
em
= 0 . (2.188)

72 2. Review of Relativistic Field Theory
Charge conservation must obviously hold both for the transition current (2.177)
of a pointlike pion,
−i∂
µ
j
µ
(π
+
) = q
µ
j
µ
(π
+
) = 0 , q ·( p + p
) = 0 , (2.189)
and for the current
q
µ
π
+
p
|
ˆ
j
µ
(0)|π
+
p=0 . (2.190)
Both conditions thus demand in general that
q
µ
Γ
µ
=q
µ
e
F(q
2
)( p + p
)
µ
+G(q
2
)q
µ
= 0 . (2.191)
The first term always vanishes since q ·( p + p
) = 0 owing to (2.183). Only the
second term will not always vanish, if q
2
= 0, so that (2.191) can only be satisfied
if
G(q
2
) = 0 . (2.192)
In other words, gauge invariance of the theory leads automatically to the state-
ment that all structural effects of the pion (mainly caused by the strong interac-
tion) can be described by a form factor as a function of the photon mass q
2
.We
thus find that
(Γ
µ
)
n.s.
=e( p
+ p)
µ
,(Γ
µ
)
w.s.
= eF(q
2
)( p
+ p)
µ
, (2.193)
where the subscript “w.s.” indicates “with structure”. Since the charge e appears
as a prefactor, (2.193) also contains the definition of charge in the sense that the
form factor at vanishing four-momentum transfer (q
2
=0) must be unity:
F(0) = 1 . (2.194)
The form factor is measured in scattering processes for all values of q
2
, both
for q
2
≤0 (timelike four-momenta measured in e
−
π
+
scattering) and q
2
≥4M
2
(timelike four-momenta in the “crossing reaction” e
+
e
−
→π
+
π
−
). Naturally
these measurements ask new questions of the theory in order to explain the form
factor F(q
2
). For physical reasons, we are led to expect that F(q
2
) diminishes
when |q
2
| is increased, since it becomes increasingly difficult to transfer mo-
mentum to the various constituents of the pion in order that it stays intact (elastic
scattering as opposed to inelastic scattering).
2.3 Fermion–Boson and Fermion–Fermion Scattering 73
EXAMPLE
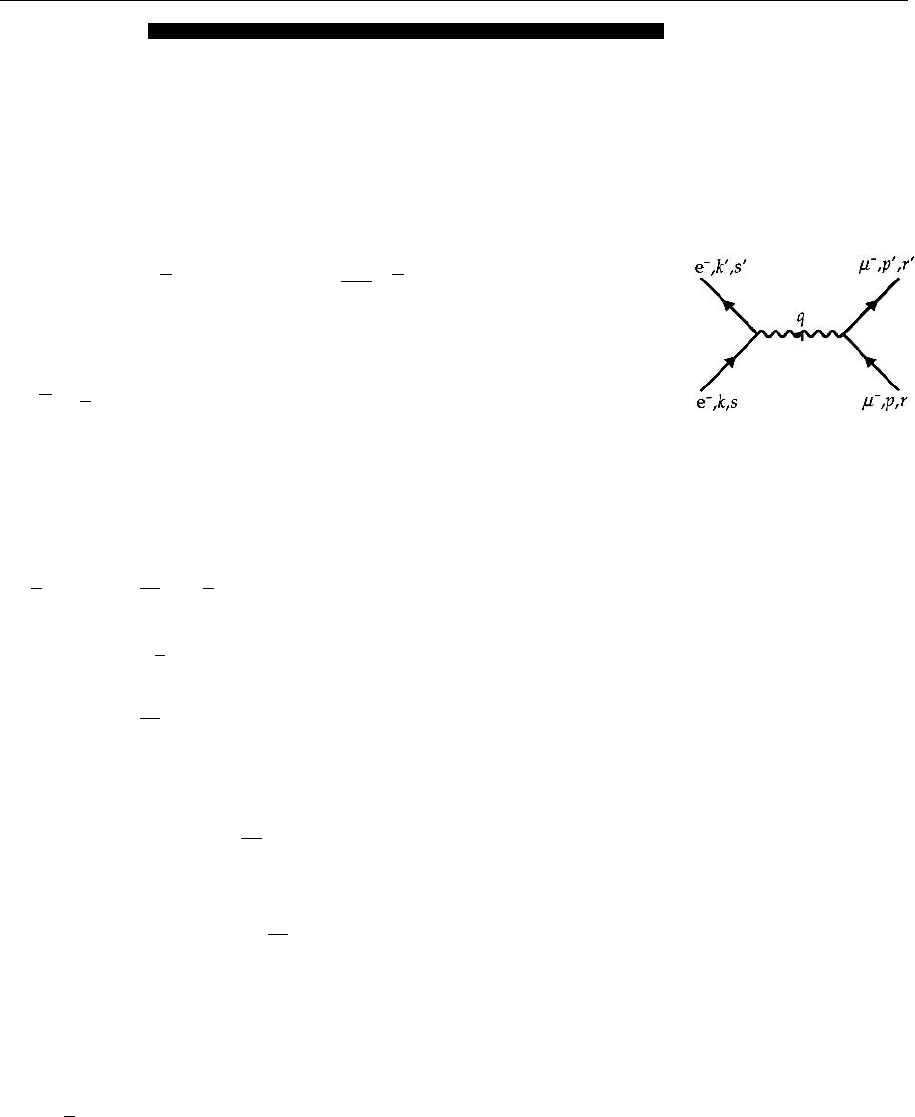
2.13 Electron–Muon Scattering
As an example of lepton–lepton scattering we briefly discuss e
−
µ
−
scattering,
which is represented in the one-photon-exchange approximation by the follow-
ing graph. Using the experiences of previous problems we can immediately
write down the invariant scattering amplitude, which now depends on four spin
indices:
F
sr;s
r
= (−e)
2
u(k
, s
)γ
µ
u(k, s)
−
g
µν
q
2
u(p
, r
)γ
µ
u(p, r). (1)
Again the nonpolarized cross section is proportional to the square of this
amplitude averaged over initial spins and summed over final spins, i.e.,
d
σ =
1
4
r,s,r
,s
F
sr;s
r
2
. (2)
We can perform the same steps as for e
−
π
+
scattering (cf. (2.161)–(2.172))
for each transition current separately. This simplification is caused by the
factorization of the currents in the one-photon-exchange approximation. We
obtain
1
4
r,s,r
,s
=
e
2
q
2
2
1
2
tr
$
(k/
+m
0
)γ
µ
(k/ +m
0
)γ
ν
%
×
1
2
tr
$
( p/
+M
0
)γ
µ
( p/ +M
0
)γ
ν
%
≡
e
2
q
2
2
L
µν
M
µν
. (3)
Employing our previous results (2.172) we can immediately write down the
electron tensor
L
µν
=2
k
µ
k
ν
+k
ν
k
µ
+
q
2
2
g
µν
(4)
and the muon tensor
M
µν
= 2
p
µ
p
ν
+ p
ν
p
µ
+
q
2
2
g
µν
. (5)
In order to obtain the cross section we have to evaluate the contraction of
these two tensors L
µν
M
µν
. The direct evaluation is straightforward but quite
lengthy. We prefer to employ the following trick, which follows from the current
conservation. Because q
µ
=k
µ
−k
µ
, the electron current conservation
∂
µ
j
µ
(e
−
) = 0 ,
q
µ
u(k
, s
)γ
µ
u(k, s)
=0(6)
Fig. 2.24. The one-photon-
exchange amplitude for
e
−
µ
−
scattering

74 2. Review of Relativistic Field Theory
Example 2.13
can be written as
u(k
, s
)
k/
−k/
u(k, s) = 0 . (7)
Equation (7) can be explicitly obtained from the corresponding Dirac equations
for
u
k
, s
and u
(
k, s
)
, respectively, and is valid for all possible spin projec-
tions. But since L
µν
is a product of two transition currents, we immediately
get
q
µ
L
µν
=q
ν
L
µν
=0 . (8)
This result is very useful because in evaluating the contraction L
µν
M
µν
we can
omit all terms proportional to q. Therefore we are able to simplify the quantities
p
= p +q and to consider the so-called effective muon tensor
M
µν
eff
=2
2p
µ
p
ν
+
q
2
2
g
µν
, (9)
which yields the same result for the contraction to be calculated, i.e.,
L
µν
M
µν
= L
µν
M
µν
eff
. (10)
A straightforward but cumbersome calculation yields the following result for the
nonpolarized cross section in the rest frame of the muon ( p
µ
= (M, 0, 0, 0)):
d
σ
dΩ
=
d
σ
dΩ
n.s.
1 −
q
2
tan
2
θ
2
2M
2
, (11)
where θ denotes the angle between k and k
. The following remarks should be
noted:
1.
(
d
σ/dΩ
)
n.s.
is the no-structure cross section known from e
−
π
+
scattering
(cf. (2.173) and (2.176)). It is modified by an additional term proportional to
tan
2
(θ/2). This effect is caused by the spin-
1
2
nature of the muon. The muon has
not only a charge but also a magnetic moment. The latter is automatically taken
into account by the Dirac equation. In other words, compared with e
−
π
+
scat-
tering, we observe an additional scattering by the normal magnetic moment in
the case of e
−
µ
−
scattering.
2. The electron rest mass was neglected in the kinematics of (11), i.e., we
considered only the ultrarelativistic limit.
3. We wrote down the e
−
π
+
as well as the e
−
µ
−
cross sections in the rest sys-
tem of the π
+
and µ
−
, respectively, which can hardly be realized in experimental
setups. Later this kind of cross section for structureless particles will be useful
in the discussion of the quark–parton model. One has to understand these cross
sections in order to acknowledge the physical content of parton dynamics.
4. The crossed reaction e
+
e
−
→µ
+
µ
−
is frequently investigated in electron–
positron collisions in the context of so-called colliding-beam experiments.Itis
also important for testing the quark–parton model if compared with the reaction
e
+
e
−
→hadrons .

2.3 Fermion–Boson and Fermion–Fermion Scattering 75
An analogous calculation leads to the cross section
d
σ
dΩ
=
α
2
4q
2
1 +cos
2
θ
, (12)
where all variables are defined in the center-of-mass system of the e
+
e
−
pair and
all masses are neglected (ultrarelativistic limit). θ denotes the angle between the
axis of the incoming and the axis of the outgoing particles.
Example 2.13
