Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

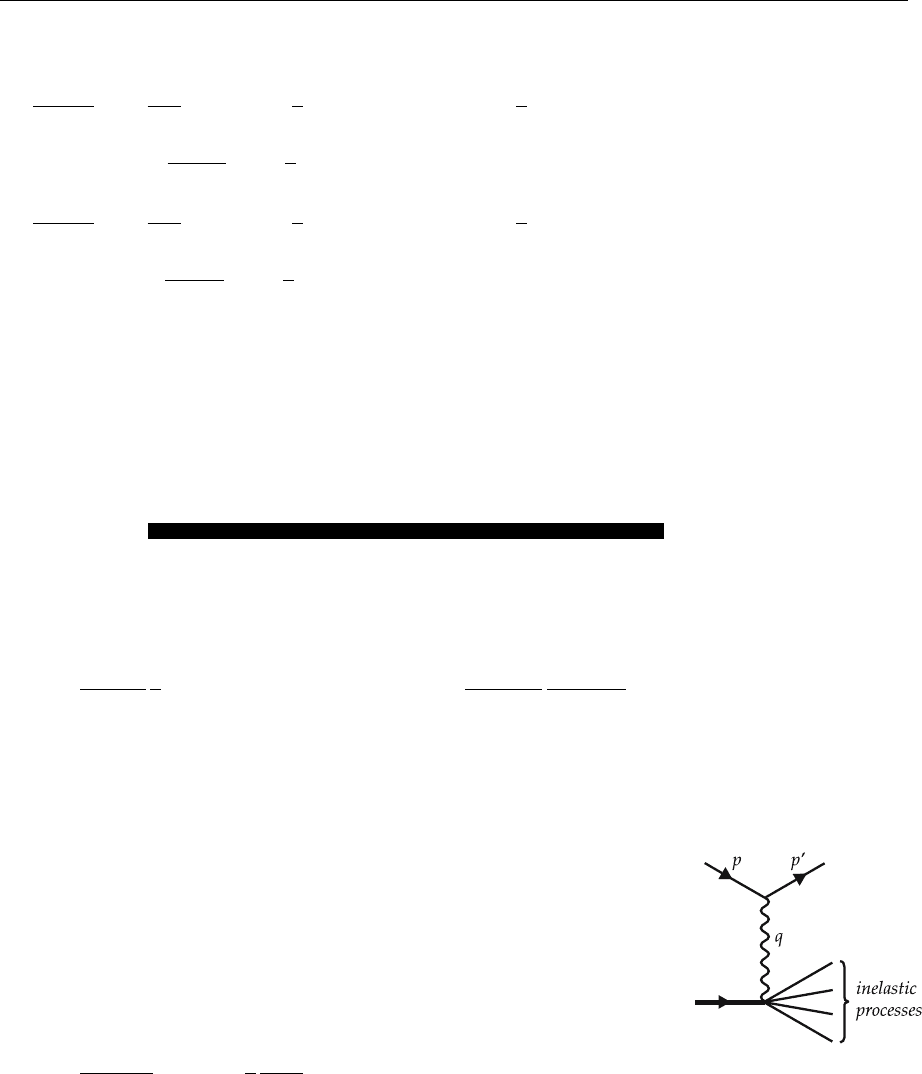
3.2 The Description of Scattering Reactions 87
and antineutrino–nucleon scattering. These formulas again hold in the rest
system of the nucleon, i.e., in the laboratory system:
d
2
σ
dE
dΩ
νN
=
G
2
F
2π
2
E
2
2sin
2
θ
2
W
νN
1
Q
2
,ν
+cos
2
θ
2
W
νN
2
Q
2
,ν
−
E +E
M
N
sin
2
θ
2
W
νN
3
Q
2
,ν
, (3.37)
d
2
σ
dE
dΩ
¯
νN
=
G
2
F
2π
2
E
2
2sin
2
θ
2
W
¯
νN
1
Q
2
,ν
+cos
2
θ
2
W
¯
νN
2
Q
2
,ν
+
E +E
M
N
sin
2
θ
2
W
¯
νN
3
Q
2
,ν
. (3.38)
Here G
F
is the Fermi coupling constant of weak interactions. The derivation of
these relations is to be found in Exercises 3.3 and 3.4.
An important assumption we have made tacitly up to now is that single-
photon and single-W exchange dominate the cross section. This assumption is
safe because of the smallness of the coupling constants. For strongly interact-
ing particles the situation becomes more complicated. Such reactions will be
analyzed in detail in Chap 6.
EXAMPLE
3.1 Normalization and Phase Space Factors
We start with the relation (see (2.116))
dσ =
1
4Eω|v |
1
2
s,s
|
F
ss
|
2
(2π)
4
δ
4
(k
+ p
−k − p)
d
3
k
(2π)
3
2ω
d
3
p
(2π)
3
2E
,
(1)
where (E, p ), (E
, p
), (ω, k) and (ω
, k
) denote the four-momenta of the
incoming electron, the outgoing electron, the incoming nucleon, and the out-
going multihadron state, respectively. Now we have to integrate this expression
over k
and, in contrast to elastic electron–pion scattering (see Exercise 2.9), also
over ω
,sinceω
is no longer fixed by k
. In elastic e–N scattering k
2
=m
2
N
.In
inelastic e–N scattering, however,
k
2
=(k +( p − p
))
2
=(k +q)
2
≥ m
2
N
,
i.e., the outgoing nucleon is no longer on the mass shell. Therefore, the energy ω
of the outgoing nucleon becomes an independent variable. Inelasticity opens, so
to speak, a new degree of freedom (see Figure 3.3a). Hence (1) becomes
dσ =
d
3
p
4EE
|
v
|
d
4
k
⎛
⎝
1
2
1
4ωω
s,s
|
F
ss
|
2
⎞
⎠
(2π)
−2
δ
4
(k
+ p
−k − p).
(2)
Fig. 3.3a. Inelastic scatter-
ing process. The nucleon
fragments into a baryon and
a number of pions.

88 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.1
Obviously, the dimension of the integrals has changed by one, implying that the
structure function has got an additional dimension of 1/energy. This is why we
shall later on define the dimensionless structure function F
1
as F
1
= W
1
M
N
.The
integral on the right-hand side is equal to e
4
L
µν
W
µν
/Q
4
. Note that the nucleon
normalization factors 2ω and 2ω
are included in W
µν
(see (3.11)) and that L
µν
contains the factor 1/2, which is due to spin averaging (see (3.20)). Thus (2) can
be written as
dσ =
d
3
p
4EE
|
v
|
e
4
(2π)
2
Q
4
L
µν
W
µν
. (3)
For our case (a massless electron incident on a resting nucleon)
|v|≈c = 1 . (4)
Furthermore we employ
d
3
p
= ( p
)
2
d
p
dΩ
≈ E
2
dE
dΩ (5)
and in this way obtain (3.22):
d
2
σ
dE
dΩ
=
E
E
e
4
(4π)
2
Q
4
L
µν
W
µν
=
E
E
α
2
Q
4
L
µν
W
µν
. (6)
Comparing with (2) we find
L
µν
W
µν
=
d
4
k
(2ω
)(2π)
3
1
4ω
s,s
˜
F
s,s
2
(2π)
3
δ
4
(k
+ p
−k − p),
(7)
where we factored out the photon propagator and the elementary charges
F
s,s
2
=
e
4
Q
4
˜
F
s,s
2
. The integral
+
d
4
k/(2ω
)(2π)
3
corresponds to a complete
sum
X,P
X
over the outgoing multihadron state, and the delta function will be
absorbed in the definition of the hadronic tensor (see (4) of Example 3.2).
EXAMPLE
3.2 Representation of W
µν
by Electromagnetic Current Operators
The coupling of the exchanged photon to the nucleon can be written in a general
way as
ˆ
J
µ
(x)A
µ
(x), (1)
where for the moment no assumption about the structure of
ˆ
J
µ
(x) has been made.
Now we consider the corresponding current matrix element between the initial

3.2 The Description of Scattering Reactions 89
nucleon state with momentum P
µ
and an arbitrary hadronic final state X with
four-momentum P
X,µ
:
,
X(P
X
)
ˆ
J
µ
(x)
N(P)
=
-
X(P
X
)
ˆ
J
µ
(0)
N(P)
.
e
−i(P−P
X
)·x
. (2)
In order to evaluate the inclusive cross section, (2) is squared and summed over
all X states:
X,P
X
-
N(P)
ˆ
J
µ
(0)
X(P
X
)
.-
X(P
X
)
ˆ
J
ν
(0)
N(P)
.
. (3)
In addition we have to average the spin of the incoming nucleon, since this
quantity is not observed. Finally energy-momentum conservation is ensured by
a δ function, which is due to the integration over x:
W
µν
=
1
2
pol.
X,P
X
-
N(P)
ˆ
J
µ
(0)
X(P
X
)
.-
X(P
X
)
ˆ
J
ν
(0)
N(P)
.
×(2π)
3
δ
4
(P
X
− P −q). (4)
q denotes the momentum of the virtual photon (see Fig. 3.3a). The δ func-
tion arises from the transition amplitude for the scattering process, which is
proportional to
d
4
yd
4
x
ˆ
J
µ
e
(y)
e
−iq·(x−y)
q
2
ˆ
J
µ
N
(x),
where
ˆ
J
µ
e
(y) and
ˆ
J
µ
N
(x) represent the electron and nucleon transition currents,
respectively. The latter one, which is in fact explicitly given by (2), also reveals
its x dependence. The x integration then yields
d
4
xe
−iq·x
e
−i( P−P
X
)·x
= (2π)
4
δ
4
(P
X
− P −q).
Squaring the amplitude implies also a squaring of the δ function, which yields
in the well-known way
(2π)
4
δ
4
(P
X
− P −q)
2
=(2π)
4
δ
4
(P
X
− P −q)VT ,
where VT is the space–time normalization volume which drops out when the
transition rate and cross section are finally calculated. At the end of Example 3.1
above we indicated that the factor (2π)
3
occurs instead of the usual factor (2π)
4
in the definition of the structure function. The summation of the projection op-
erator |X(P
X
)X(P
X
)| in (4) has the form of a complete projection operator.
But the completeness relation cannot be employed yet, since the argument of the
δ function depends on P
X
.
Using the integral representation
δ
4
(P
X
− P −q) =
d
4
y
(2π)
4
e
−i(P
X
−P−q)·y
, (5)
Example 3.2

90 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.2
we can write (4) in the form
W
µν
=
1
2
pol.
X,P
X
1
2π
d
4
y
-
N(P)
ˆ
J
µ
(0)
X(P
X
)
.
×
-
X(P
X
)
ˆ
J
ν
(0)
N(P)
.
e
−i(P
X
−P)·y
e
iq·y
=
1
4π
pol.
X,P
X
d
4
y
-
N(P)
ˆ
J
µ
(y)
X(P
X
)
.-
X(P
X
)
ˆ
J
ν
(0)
N(P)
.
e
iq·y
,
(6)
where
ˆ
J
µ
(y) has been obtained by means of (2). Now we are able to employ the
completeness relation
X,P
X
|X(P
X
)X(P
X
)|=1 , (7)
which yields the expression for W
µν
(P, q) given in (3.33):
W
µν
(P, q) =
1
4π
pol.
d
4
y e
iq·y
-
N(P)
ˆ
J
µ
(y)
ˆ
J
ν
(0)
N(P)
.
. (8)
Now it is interesting to note that instead of the operator product
ˆ
J
µ
(y)
ˆ
J
ν
(0) also
the expectation value of the commutator of the current operators could be used
in (8), i.e.,
W
µν
=
1
4π
pol.
d
4
y e
iq·y
-
N(P)
ˆ
J
µ
(y)
ˆ
J
ν
(0)
N(P)
.
. (9)
In order to show the equivalence of (8) and (9) one has to prove that the following
expression vanishes:
d
4
y e
iq·y
-
N(P)
ˆ
J
ν
(0)
ˆ
J
µ
(y)
N(P)
.
=
X,P
X
d
4
y e
iq·y
-
N(P)
ˆ
J
ν
(0)
X(P
X
)
.-
X(P
X
)
ˆ
J
µ
(y)
N(P)
.
=
X,P
X
d
4
y e
i(q+P
X
−P)·y
-
N(P)
ˆ
J
ν
(0)
X(P
X
)
.-
X(P
X
)
ˆ
J
µ
(0)
N(P)
.
= (2π)
4
X,P
X
δ
4
(P
X
− P +q)
-
N(P)
ˆ
J
ν
(0)
X(P
X
)
.-
X(P
X
)
ˆ
J
µ
(0)
N(P)
.
.
(10)
The energy δ function requires that E
X
= P
0
−q
0
= M
N
−(E −E
)<M
N
holds in the lab system. However, such a state X does not exist, since the nucleon
is the state of lowest energy with baryon number 1. Therefore (10) vanishes and
(9) is proved.

3.2 The Description of Scattering Reactions 91
EXERCISE
3.3 The Nucleonic Scattering Tensor with Weak Interaction
Problem. Repeat the discussion leading from (3.6) to (3.18) assuming that par-
ity is not conserved, i.e., that Γ
µ
consists of Lorentz vectors and Lorentz axial
vectors. Take into account that time-reversal invariance still holds.
Solution. Have a look at Fig. 3.2. We are again discussing the elastic process de-
scribed by that figure, but allow for non-parity-conserving currents. In this case
the transition current is of the general form
¯
u(P
)Γ
µ
u(P) = B(P
µ
+ P
µ
)S +iC(P
µ
− P
µ
)S + AV
µ
+D(P
ν
+ P
ν
)T
µν
+iE(P
ν
− P
ν
)T
µν
+B
(P
µ
+ P
µ
)P +iC
(P
µ
− P
µ
)P + A
A
µ
+D
(P
ν
+ P
ν
)ε
µναβ
T
αβ
+iE
(P
ν
− P
ν
)ε
µναβ
T
αβ
(1)
with real functions A, B, C, ... and with
S =
¯
u(P
) u(P) scalar ,
P =
¯
u(P
) i γ
5
u(P) pseudoscalar ,
V
µ
=
¯
u(P
)γ
µ
u(P) vector ,
A
µ
=
¯
u(P
)γ
µ
γ
5
u(P) pseudovector ,
T
µν
=
¯
u(P
)σ
µν
u(P) tensor . (2)
In (1) we have assumed that the transition current is real, i.e.
¯
u(P
)Γ
µ
u(P)
†
=
¯
u(P
)Γ
µ
u(P)
and therefore
u
†
(P)γ
0
γ
0
Γ
†
µ
γ
0
u(P
) =
¯
u(P)Γ
µ
u(P
).
Here the relation γ
0
Γ
†
µ
γ
0
=Γ
µ
was used, which can easily be verified in the
standard representation of the γ
µ
and σ
µν
=
i
2
γ
µ
,γ
ν
. Obviously, the exchange
P ↔ P
should have the same effect as complex conjugation. In other words, the
right-hand side must therefore be invariant under the transformation
(···)
∗
P
µ
↔P
µ
. (3)
Time inversion yields (see Table 2.1)
S → S , P →−P , V
µ
→ V
µ
, A
µ
→ A
µ
, T
µν
→−T
µν
, (4)
and
P ↔−P
, P
0
↔ P
0
, i.e. P
µ
↔ P
µ
. (5)

92 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.3
The transition P ↔−P
, P
0
↔ P
0
is due to the complex conjugation of
¯
u(P
)Γ
µ
u(P), which replaces the momentum P
µ
by the negative value of P
µ
and vice versa, i.e., P
µ
↔−P
µ
. Because t →−t there is an additional change in
the sign of the zero component. This is easily understood, because under time re-
versal the direction of motion changes and initial and final states are exchanged.
The energies, however, remain positive.
Under combined transformations (4) and (5), (1) assumes the form
¯
u(P
)Γ
µ
u(P)→B(P
µ
+ P
µ
)S −iC(P
µ
−P
µ
)S + AV
µ
−D(P
ν
+ P
ν
)T
µν
+iE(P
ν
− P
ν
)T
µν
−B
(P
µ
+ P
µ
)P +iC
(P
µ
− P
µ
)P + A
A
µ
−D
(P
ν
+ P
ν
)ε
µναβ
T
αβ
+iE
(P
ν
− P
ν
)ε
µναβ
T
αβ
. (6)
Only the spatial components of the current vector should change sign under
time reversal. In order to conserve T invariance (6) must therefore be equal
to
¯
u(P
)Γ
µ
u(P).Fortheε tensor the relation ε
µναβ
=−ε
µναβ
holds. This
can be verified from the definition −4iε
µναβ
=tr
γ
5
γ
µ
γ
ν
γ
α
γ
β
. The indices
µ, ν, α, β have to be 0, 1, 2, 3, and different from each other. Now −4iε
0,1,2,3
=
tr
γ
5
γ
0
γ
1
γ
2
γ
3
=−tr
[
γ
5
γ
0
γ
1
γ
2
γ
3
]
=+4iε
0,1,2,3
. For different permutations
of 0, 1, 2, 3 the analogous relation holds. Employing now ε
µναβ
=−ε
µναβ
we
have
C = D = B
= E
= 0 . (7)
Because of the Gordon decomposition (see earlier text and (3.10)), E can again
be replaced by A and B. In an analogous way D
can also be eliminated using A
and C
. In order to derive this identity we consider the expression
¯
u(P
)
−2M
N
a/γ
5
+
#
P/
− P/
2
, a/
&
+
γ
5
+
P/
+ P/
2
, a/
−
γ
5
u(P)
=
¯
u(P
)
−2M
N
a/γ
5
+ P/
a/γ
5
−a/P/γ
5
u(P)
=
¯
u(P
)
(
−2M
N
a/γ
5
+M
N
a/γ
5
+a/γ
5
M
N
)
u(P)
= 0 . (8)
Differentiating this relation with respect to a
µ
yields
∂
∂a
µ
a
α
γ
α
= δ
α
µ
γ
α
= γ
µ
and we obtain
¯
u(P
)
−2M
N
γ
µ
γ
5
+(P
− P)
λ
1
2
$
γ
λ
,γ
µ
%
γ
5
+ (P
+ P)
λ
1
2
γ
λ
,γ
µ
γ
5
u(P). (9)

3.2 The Description of Scattering Reactions 93
With (1/2)
$
γ
λ
,γ
µ
%
= g
λ,µ
and (1/2)
γ
λ
,γ
µ
=−iσ
λ,µ
and with (8) we there-
fore conclude that
0 =−2M
N
A
µ
+
¯
u(P
)
(P
µ
− P
µ
)γ
5
−i(P
ν
+ P
ν
)σ
νµ
γ
5
u(P)
=−2M
N
A
µ
−i(P
µ
− P
µ
)P −
1
2
ε
µναβ
T
αβ
(P
ν
+ P
ν
), (9b)
which represents the desired result. Consequently we have reduced (1) to
¯
u(P
)Γ
µ
u(P) = B(P
µ
+ P
µ
)S + AV
µ
+iC
(P
µ
− P
µ
)P + A
A
µ
. (10)
Here the letters B, A, C
,andA
denote constants while S, V
µ
, P,andA
µ
stand
for the various currents denoted in (2). Similarly, as in (3.11), W
µν
then becomes
W
µν
= tr
#
Aγ
µ
+B(P
µ
+ P
µ
)
+ A
γ
µ
γ
5
+C
(P
µ
− P
µ
)γ
5
)
(P/
+M
N
)
Aγ
ν
+B(P
ν
+ P
ν
)
+ A
γ
ν
γ
5
−C
(P
ν
− P
ν
)γ
5
(P/ +M
N
)
&
= tr
Aγ
µ
+B(P
µ
+ P
µ
)
(P/
+M
N
)
Aγ
ν
+B(P
ν
+ P
ν
)
(P/ +M
N
)
+tr
A
γ
µ
+C
(P
µ
+ P
µ
)
(−P/
+M
N
)
−A
γ
ν
−C
(P
ν
− P
ν
)
(P/ +M
N
)
+tr
$
A
γ
µ
γ
5
P/
Aγ
ν
P/ + Aγ
µ
P/
A
γ
ν
γ
5
P/
%
.
(11)
Note again that we have used the normalization for the u and v spinors expressed
in (2.50). The first two traces do not have to be evaluated explicitly. It is sufficient
to know that because P
µ
=q
µ
+ P
µ
their contribution can only be of the form
g
µν
V
1
+ P
µ
P
ν
V
2
+(P
µ
q
ν
+ P
ν
q
µ
)V
3
+q
µ
q
ν
V
4
. (12)
In the case of the last trace the identity
tr
$
γ
5
a/b/c/d/
%
= 4iε
µναβ
a
µ
b
ν
c
α
d
β
holds. Therefore the hadronic tensor is of the form
W
µν
= g
µν
V
1
+ P
µ
P
ν
V
2
+(P
µ
q
ν
+ P
ν
q
µ
)V
3
+q
µ
q
ν
V
4
+iε
µναβ
P
α
q
β
V
5
.
(13)
We have derived (13) for elastic lepton–nucleon scattering. In the case of inelas-
tic processes, including particle creation, q
µ
= P
µ
− P
µ
is no longer valid. q · P
,
q
2
and q · P are then independent quantities. However, the results again are quite
simple if one sums over all possible final states, i.e., over the final states of the
reactions
ν
e
( p) +N(P) → e
−
( p −q) +X ,
¯
ν
e
( p) +N(P) → e
+
( p −q) +X . (14)
Exercise 3.3
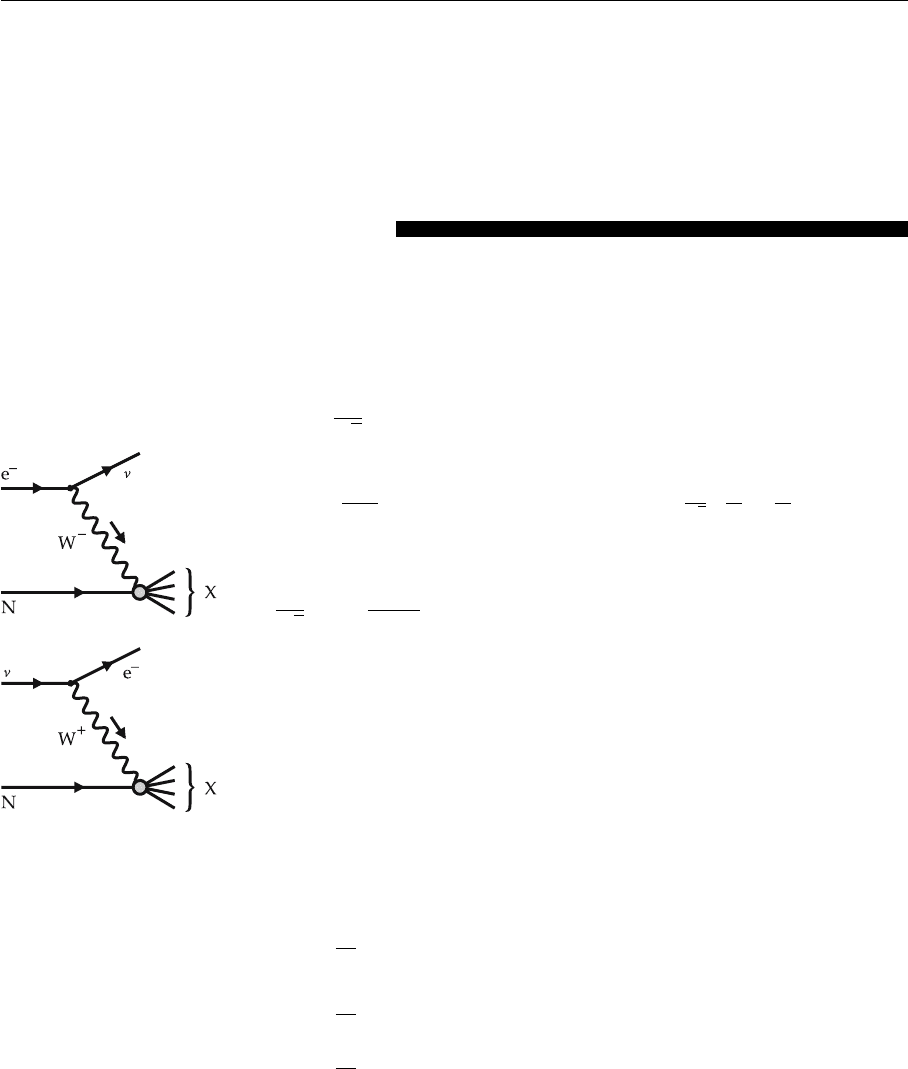
94 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.3
Fig. 3.3b. Deep inelastic
scattering with charged vec-
tor bosons.
Therefore the inclusive inelastic scattering tensor for parity-violating lepton–
nucleon scattering is
W
µν
=g
µν
V
1
(Q
2
,ν)+ P
µ
P
ν
V
2
(Q
2
,ν)+(P
µ
q
ν
+ P
ν
q
µ
)V
3
(Q
2
,ν)
+q
µ
q
ν
V
4
(Q
2
,ν)+iε
µναβ
P
α
q
β
V
5
(Q
2
,ν) . (15)
EXERCISE
3.4 The Inclusive Weak Lepton–Nucleon Scattering
Problem. The coupling of the charged vector bosons W
±
µ
of the weak interac-
tion to leptons is described by the interaction Lagrangean (4.23),
L
int
=
+g
√
2
¯
Ψ
f
(
ˆ
T
−
W
+
µ
+
ˆ
T
+
W
−
µ
)γ
µ
Ψ
f
, (1)
where Ψ
f
=
ν
e
e
L
denotes the doublet of the left-handed electron–neutrino
field: e
L
=
1−γ
5
2
e
L
. Writing (1) we have used
ˆ
T
±
=
1
√
2
λ
1
2
±i
λ
2
2
. With
ˆ
T
−
=
00
10
and
ˆ
T
+
=
01
00
we get for the fundamental (e,
¯
ν) interaction
+g
√
2
¯
ν(x)γ
µ
1 −γ
5
2
e(x)W
µ
(x) +h.c.. (1a)
The corresponding processes are depicted in the figure. Derive from this equation
the leptonic scattering tensor L
µν
. Employ the result of Exercise 3.3 to evaluate
the differential cross section for the inclusive weak lepton–nucleon scattering.
Solution. Since the neutrino is massless and the electron mass can be neglected,
it is helpful to choose the following spinor normalization.
u
†
α
( p)u
β
( p) = 2Eδ
αβ
,
spin
u(p)
¯
u(p) = p/ +m = p/. (2)
The leptonic scattering tensor is then
L
µν
=
g
2
8
s
tr
¯
ν(p)γ
µ
(1 −γ
5
)e(p
, s)
¯
e(p
, s)γ
ν
(1 −γ
5
)ν( p)
=
g
2
8
tr
p/γ
µ
(1 −γ
5
) p/
γ
ν
(1 −γ
5
)
(utilizing (2)))
=
g
2
4
tr
p/γ
µ
p/
γ
ν
−tr
γ
5
p/
γ
ν
p/γ
µ
= g
2
p
µ
p
ν
+ p
µ
p
ν
− p
· pg
µν
−iε
µναβ
p
α
p
β
. (3)

3.2 The Description of Scattering Reactions 95
Since the neutrino is always left-handed, there is no averaging of the initial
spin. Nevertheless, in order to obtain the trace in the second line of (3) we have
summed over all neutrino spins and made use of (2). This procedure is correct,
because the operator (1 −γ
5
) cancels the contribution of the nonphysical right-
handed neutrino state. In analogy to (3.22) the differential cross section then
becomes
d
2
σ
dE
dΩ
=
E
(4π)
2
E
1
q
2
−M
2
W
2
L
µν
g
√
2
2
W
µν
. (4)
The differences can be explained as follows.
(1) The propagator for massive W bosons differs from that for massless photons.
For |q
2
|M
2
W
we can use
1
q
2
−M
2
W
2
≈
1
M
4
W
. (5)
This yields Fermi’s theory of weak interaction.
(2) The coupling constant of the W bosons to the nucleon is effectively chosen
to be G
F
/
√
2whereG
F
= g
2
/(4
√
2M
2
W
) is the Fermi constant of weak interac-
tion. Since we have already absorbed a factor of g
2
/8 (see (3)) in the definition of
the leptonic tensor we are left with a factor of g
2
/(4 ·2) in front of the hadronic
tensor W
µν
, which according to (3.11) does not contain any coupling constant.
(3) The factor 1/(4π)
2
arises by replacing α
2
=e
4
/(4π)
2
→ g
4
/(4π)
2
.One
factor g
2
is contained in L
µν
, the other one appears explicitly in (4).
In order to evaluate (4) we first show that q
µ
L
µν
and q
ν
L
µν
vanish:
q
µ
L
µν
= g
2
q · p
p
ν
+q · pp
ν
− p
· pq
ν
−iε
µναβ
q
µ
p
α
p
β
= g
2
−
q
2
2
p
ν
+
q
2
2
p
ν
+
q
2
2
( p
ν
− p
ν
)
=0 . (6)
Here we have employed
q
µ
= p
µ
− p
µ
⇒ p · p
=−
q
2
2
,
p ·q =
q
2
2
and p
·q =−
q
2
2
, (7)
which all hold in the high-energy limit m
2
q
2
. With help of 15 from Exer-
cise 3.3 it therefore follows that
L
µν
W
µν
= L
µν
g
µν
V
1
+ P
µ
P
ν
V
2
+iε
µναβ
P
α
q
β
V
5
= g
2
(2 p
· p −4 p
· p)V
1
+
2 p
· Pp·P −M
2
N
p · p
V
2
+ε
µν
αβ
ε
µνδγ
p
δ
q
γ
P
α
q
β
V
5
. (8)
Exercise 3.4
96 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.4
With
p = (E, p ), p
= (E
, p
), P = (M, 0 ), (9)
and
8
ε
µν
αβ
ε
µνδγ
=−2
g
αδ
g
βγ
−g
αγ
g
βδ
, (10)
and, also, utilizing relations (7) this assumes the form
L
µν
W
µν
= g
2
q
2
V
1
+M
2
N
2EE
+
1
2
q
2
V
2
−2
p · Pq
2
− P ·qp·q
V
5
= g
2
#
q
2
V
1
+2M
2
N
EE
+
1
4
q
2
V
2
−2M
N
Eq
2
−(E −E
)
q
2
2
V
5
&
.
(11)
Again, using (3.30), we find that
q
2
=−Q
2
=−4EE
sin
2
ϑ
2
(12)
leads to
L
µν
W
µν
= g
2
2EE
−2sin
2
ϑ
2
V
1
+M
2
N
cos
2
ϑ
2
V
2
+2M
N
sin
2
ϑ
2
(E +E
)V
5
. (13)
In order to provide all structure functions with the same dimension we define
W
1
=−V
1
, W
2
= V
2
M
2
N
, W
3
=−2V
5
M
2
N
(14)
and obtain
d
2
σ
dE
dΩ
=
E
2
g
4
4M
4
W
(4π)
2
2sin
2
ϑ
2
W
1
(Q
2
,ν)+cos
2
ϑ
2
W
2
(Q
2
,ν)
−
E +E
M
N
sin
2
ϑ
2
W
3
(Q
2
,ν)
. (15)
Finally we substitute the so-called Fermi constant of weak interaction:
G
F
=
g
2
4
√
2M
2
W
; (16)
8
The proof of this relation can be found in Exercise 2.4 of W. Greiner and B. Müller:
Gauge Theory of Weak Interactions, 3rd ed. (Springer, Berlin, Heidelberg 2000).
