Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


3.2 The Description of Scattering Reactions 107
the so-called Bjorken scaling, which we now do understand within the parton
model. Equation (3.74) then becomes
2
xy
2
F
eN
1
(x) +(1 −y)F
eN
2
(x)
=
y
2
+2(1 −y)
i
f
i
(x)q
2
i
x . (3.81)
By comparing powers of y,wefindthat
F
eN
1
(x) =
1
2
i
f
i
(x)q
2
i
, F
eN
2
(x) =
i
f
i
(x)q
2
i
x , (3.82)
and
F
eN
2
(x) = 2xF
eN
1
(x). (3.83)
This is the Callan–Gross relation . Moreover, the nucleon form factors are now
– within the parton model – simply related to the parton distribution functions
f
i
(x), describing the distribution of the fraction of the total nucleon momentum
shared by the ith parton.
We have thus seen that deep inelastic scattering processes can be explained
by the basic assumptions of the parton model: the hadron is built of pointlike
constituents whose energy of interaction with each other and whose mass is small
compared to
"
Q
2
> 1GeV.
The physical foundations of (3.81) and (3.82) can also be illustrated from
a different point of view: we can assume that partons are massless. There are
no dimensional quantities in electron–parton scattering except for the momenta.
Hence, the only Lorentz-invariant quantities are q
2
, P
2
,andP ·q.Now,P
2
=
M
2
=0, because of the vanishing parton masses. From Q
2
=−q
2
and P ·q one
can only have Q
2
and the dimensionless x = Q
2
/2P ·q.SinceF
eN
1
(Q
2
, x) is
dimensionless, it can only depend on x alone, i.e. F
eN
1
(Q
2
, x) = F
eN
1
(x).
We have already seen that three structure functions are present in a parity-
violating interaction (see (3.37) and (3.38)). On the other hand, we obtain only
one structure function for scalar particles, i.e., F
1
=0 (see Exercise 3.7). In add-
ition to deep inelastic electron–nucleon scattering, photon–nucleon scattering
also yields information about structure functions. In fact, in Exercise 3.8, we
shall show that the relationship between the cross sections for transverse and
for scalar photons, in particular, is of interest, since it tests the Callan–Gross re-
lation (3.82). As can be seen from Fig. 3.6, it holds very well experimentally.
Therefore it suffices to investigate scattering reactions as a function of F
2
(x).For
this reason, Fig. 3.5 shows only F
2
(x) =
1
2
(F
ep
2
+F
en
2
).InExercise3.9weshall
finally compute the structure functions following from a simple constituent-
quark model. Independent of the special assumption of each model, all such
computations yield the following results.
(1) If one assumes that the nucleon is composed of three quarks, the one-
particle distributions f(x) are typically maximal at x = 1/3 and, accordingly, the
structure function F
2
(x) at somewhat higher values of x.
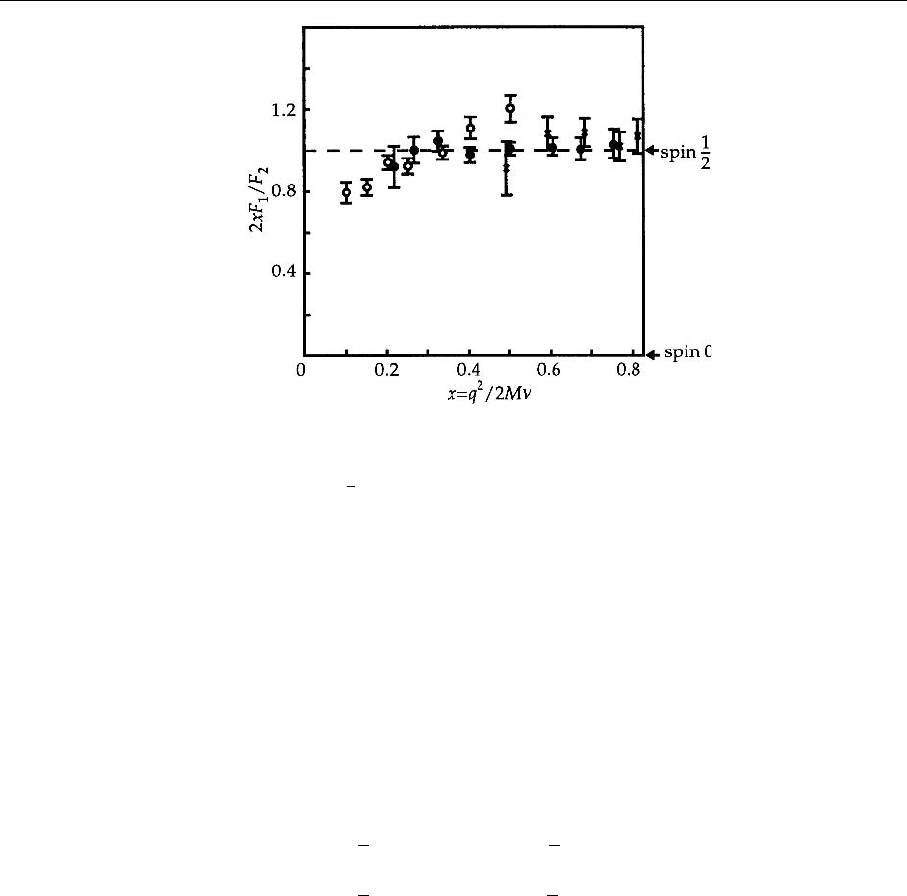
108 3. Scattering Reactions and the Internal Structure of Baryons
Fig. 3.6. The ratio of the
structure functions F
1
and F
2
within the scaling region
provides a test of the so-
called Callan–Gross rela-
tions (see (3.82))
(2) The structure functions averaged over protons and neutrons are designated
by F
2
(x) =
1
2
[F
ep
2
(x) +F
en
2
(x)],where
F
eN
2
(x) =
i
f
i
(x)q
2
i
x
= f (x) ·x
i
q
2
i
(3.84)
is the structure function for the nucleon (N =p, n). Here it is assumed that all
three quarks in the nucleon have, owing to their negligible masses, the same wave
function.
We proceed now somewhat differently then before and introduce momentum
distribution functions for quark flavors. Let us call the momentum distribution
function for an u quark u(x), the one for a d quark d(x), and those for the
corresponding antiquarks
¯
u(x),
¯
d(x),etc.Then
F
ep
2
(x) =
4
9
u
p
(x) +
¯
u
p
(x)
x +
1
9
d
p
(x) +
¯
d
p
(x)
x ,
F
en
2
(x) =
4
9
u
n
(x) +
¯
u
n
(x)
x +
1
9
d
n
(x) +
¯
d
n
(x)
x . (3.85)
Note that u(x) contains now all u quarks in the nucleon. The same is true for
¯
u(x),
d(x),
¯
d(x), etc. This is different from the f
i
(x) introduced in e.g. (3.81). There
each individual quark is counted separately with its own distribution function
f
i
(x). Here, only the distributions of the flavors are considered.
Assuming isospin symmetry, one concludes that the u
n
(x) distribution is the
same as the d
p
(x) distribution, and similarly u
p
(x) = d
n
(x). Therefore we set
u
p
(x) = d
n
(x) ≡ u(x),
d
p
(x) = u
n
(x) ≡ d(x).

3.2 The Description of Scattering Reactions 109
and similarly for the antiquarks. Hence (3.85) becomes
F
ep
2
(x) =
4
9
u(x) +
¯
u(x)
x +
1
9
d(x) +
¯
d(x)
x ,
F
en
2
(x) =
1
9
u(x) +
¯
u(x)
x +
4
9
d(x) +
¯
d(x)
x , (3.86)
and it follows that
F
2
(x) =
1
2
F
ep
2
(x) +F
en
2
(x)
=
1
2
5
9
u(x) +
¯
u(x)
+
5
9
d(x) +
¯
d(x)
x
=
5
18
u(x) +
¯
u(x)
+
d(x) +
¯
d(x)
x . (3.87)
If we sum over the momenta of all possible partons in a nucleus, the total
momentum P of the nucleon should be obtained, i.e.
1
0
dx
xP
µ
u(x) +
¯
u(x) +d(x) +
¯
d(x) +s(x) +
¯
s(x) +...
= P
µ
−
P
µ
g
. (3.88)
Here
P
µ
g
stands for the momentum carried by partons not taken into account
in the sum of the left-hand side. The index g in
P
µ
g
shall indicate that this miss-
ing momentum is possibly due to gluons. Neglecting gluons, one deduces from
(3.88) that
1
0
dxx
(u(x) +
¯
u(x) +d(x) +
¯
d(x) +s(x) +
¯
s(x) +...
= 1 , (3.89)
and it follows from (3.87) that
18
5
1
0
dxF
2
(x) = 1 . (3.90)
This relation can be tested with experiments (see Fig. 3.12 below). One finds:
(1) F
2
(x) is maximal for small x, i.e., there must be charged partons carrying
only a small momentum fraction. It is natural to identify them with quark–
antiquark pairs, which are – due to the interaction between the quarks (gluon
exchange) – also created out of the vacuum (ground state). One might better
call them vacuum ground-state correlation. A careful analysis of electromag-
netic and electroweak structure functions indeed justifies this assumption, as we
shall see below.
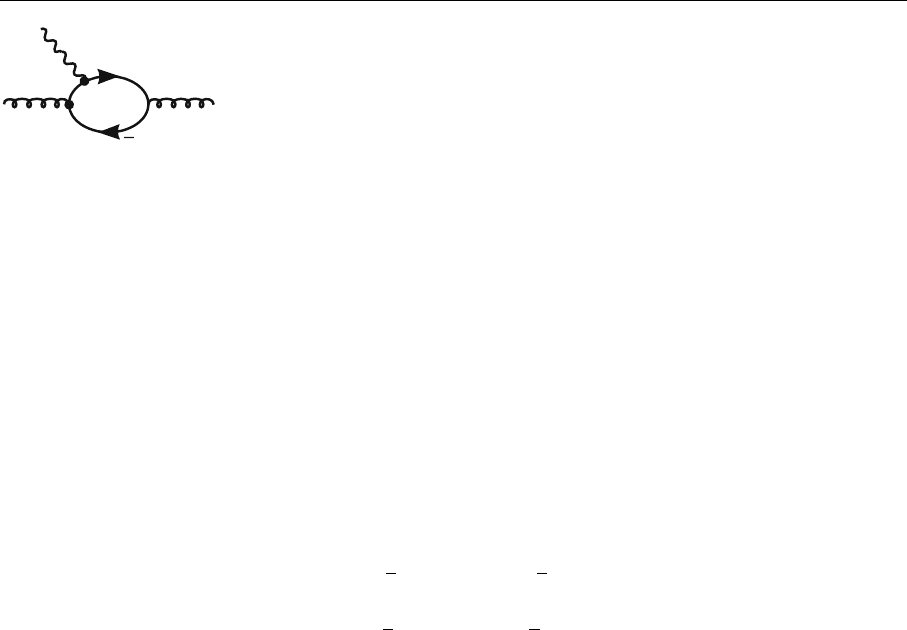
110 3. Scattering Reactions and the Internal Structure of Baryons
g*
q
q
gg
Fig. 3.7. The quark–anti-
quark pairs act effectively as
electrically neutral objects,
as do the gluons, of course.
However, there is an im-
portant difference between
quark–antiquark pairs and
gluons, namely that elec-
trons with sufficiently high
momentum transfer can al-
ways scatter from the for-
mer, but never from gluons
(2) The integral
+
dxF
2
(x) is experimentally much smaller than unity, namely
approximately 0.45. Half of the nucleon momentum is thus carried by elec-
trically neutral particles. This is an important point since, according to our
consideration above, it is the most direct evidence for the existence of gluons.
The valence quarks interact with other quark–antiquark pairs via gluons, which
leads to vacuum ground-state correlations. They can be graphically depicted as
in Fig. 3.7. We shall return to this point in Sect. 4.2.
It may be added that more-refined models are also not able to give a satisfying
description of the experimental data in Fig. 3.12 starting from the quark–quark
interaction without ad hoc assumptions. It is possible, however, to describe
the relationship between two structure functions. One can, for example, calcu-
late quite well the relative change in F
2
for different values of Q
2
.Weshall
discuss this in Chap. 5. The reason for this only partial success is that the cal-
culation of structure functions itself is a completely nonperturbative problem
and thus very difficult, while the Q
2
dependence is calculable by summing
a few classes of graphs, i.e., in perturbation theory. As mentioned above, one
introduces distribution functions for the various quarks and antiquarks:
u(x),
¯
u(x), etc.
Then (3.86) can be generalized as
F
ep
2
(x) = x
#
4
9
u(x) +
¯
u(x)
+
1
9
d(x) +
¯
d(x)
+
4
9
c(x) +
¯
c(x)
+
1
9
s(x) +
¯
s(x)
&
. (3.86a)
The crucial point is now that the structure functions for the reactions
ν
e
+n →e
−
+p, ν
e
+n →ν
e
+n, etc. involve different combinations of u(x),
¯
u(x),d(x),and
¯
d(x). (The weak charges of the quarks are not proportional to
their electric charges.) Therefore quark distributions can be deduced from the
different structure functions.
We will examplify this idea by considering the neutrino–nucleon structure
functions that are measured in the reactions
νp→e
−
X, ¯νp → e
+
X ,
νn→e
−
X, ¯νn → e
+
X. (3.91)
Due to charge conservation in these reactions the following parton distribution
functions are measured:
F
νp
2
(x) = 2x
d(x) +
¯
u(x)
,
F
¯
νp
2
(x) = 2x
u(x) +
¯
d(x)
,
F
νn
2
(x) = 2x
u(x) +
¯
du(x)
,
F
¯
νn
2
(x) = 2x
d(x) +
¯
u(x)
. (3.92)
3.2 The Description of Scattering Reactions 111
The factor of 2 reflects the presence of both vector and axial vector parts in the
weak currents. From that we get for the combination νp → e
−
Xandνn → e
−
X
F
νp
2
(x) +F
¯
ν p
2
(x) = 2x(u +
¯
u +d +
¯
d).
Combining this with (3.87) gives
F
ep
2
(x) +F
en
2
= x
5
9
(u +
¯
u +d +
¯
d) +x
2
9
(s +
¯
s)
we can extract the strange quarks content of the nucleon
F
ep
2
(x) +F
en
2
−
5
18
F
νp
2
(x) +F
¯
νp
2
(x)
=
2
9
x(s +
¯
s). (3.93)
The experimental data indicate a nonvanishing right-hand side only for the small
x ≤ 0.2region.
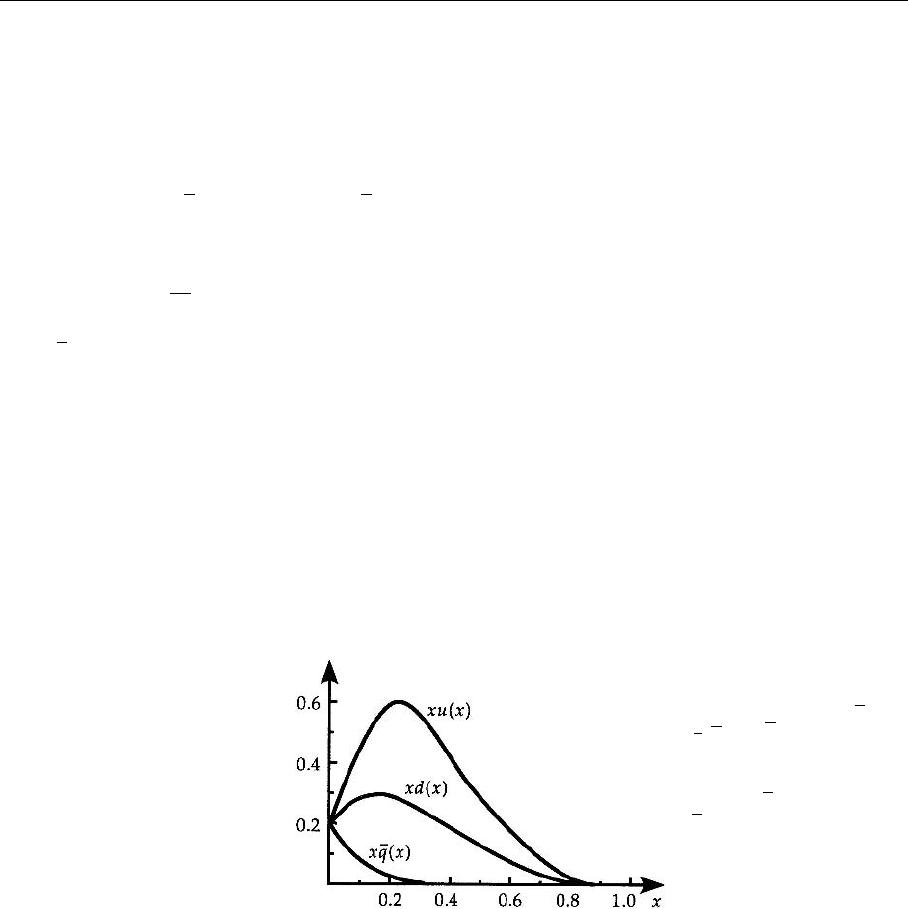
In Fig. 3.8 we have sketched approximately what the parton distributions
look like in a proton. Most interesting is the fact that quark and antiquark
distributions coincide for x → 0. This can be understood if both are vacuum
excitations (so-called sea quarks but one should better call them vacuum cor-
relations (ground-state correlations) of quark–antiquark pairs), generated by the
quark–quark interaction. The obvious divergence of the functions u(x), d(x),and
¯
q(x) for x → 0 thus indicates that the interaction is large for small momentum
transfers.
Fig. 3.8. Asketchofthe
quark distribution functions
for protons with
q(x) =
1
2
(u(x) +d(x)). It can be
recognized that the contribu-
tions of the valence quarks
x (u(x) −
q(x)) and x(d(x) −
q(x)) vanish for x → 0.
Hence vacuum excitations
in form of quark–antiquark
pairs dominate for small
values of x
112 3. Scattering Reactions and the Internal Structure of Baryons
EXERCISE
3.6 The Breit System
Problem. Prove the existence of a Lorentz reference frame where (3.61) holds.
Solution. We start with the laboratory system. Here
q
µ
=(q
0
, q), q
0
> 0 ,
P
µ
=(M, 0). (1)
First we perform a rotation in such a way that q is parallel to the z direction.
q
µ
=(q
0
, 0, 0, q
3
), q
0
, q
3
> 0
P
µ
=(M
N
, 0, 0, 0). (2)
Now we boost the system in the z direction, i.e., we transform to a reference
frame moving with the velocity
v
z
=
q
0
q
3
c = βc . (3)
This is possible, because the momentum transfer q
µ
is spacelike, i.e.,
Q
2
=q
2
3
−q
2
0
> 0 →q
3
> q
0
. (4)
This follows easily from (3.50a), according to which, Q
2
= 4EE
sin
2
θ/2 > 0.
Then in the new reference frame
q
µ
= γ(q
0
−βq
3
, 0, 0, q
3
−βq
0
)
= γ
0, 0, 0, q
3
−β
2
q
3
,β=
q
0
q
3
=
⎛
⎝
0, 0, 0, q
3
/
0
0
1
1 −
q
2
0
q
2
3
⎞
⎠
=
0, 0, 0,
"
Q
2
, (5)
with
β =
v
z
c
=
q
0
q
3
and γ =
1 −β
2
−1/2
. (6)
Under this transformation the nucleon momentum becomes
P
µ
=γ(M
N
, 0, 0, −βM
N
). (7)
Since we consider reactions where Q
2
and
ν = q
· P
=q
0
=q
· P
(8)
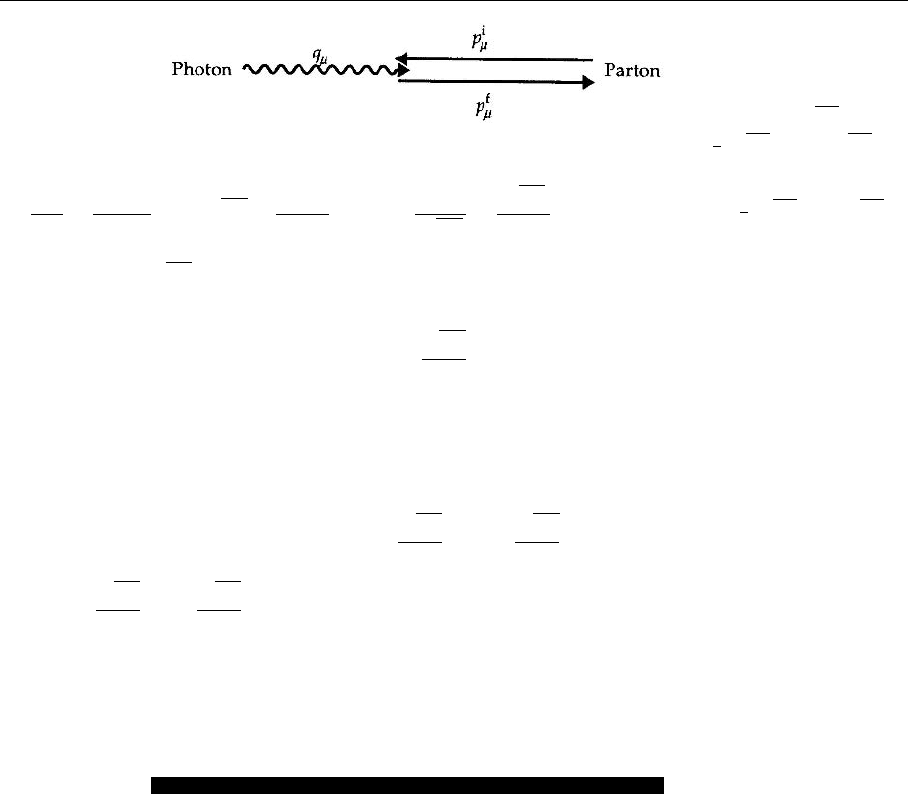
3.2 The Description of Scattering Reactions 113
Fig. 3.9. Photon–parton in-
teraction in the Breit system.
The initial photon and par-
ton carry the four-momenta
q
µ
= (0, 0, 0,
"
Q
2
) and P
f
µ
=
1
2
(
"
Q
2
, 0, 0, −
"
Q
2
),re-
spectively. The final par-
ton then has the momentum
P
f
µ
=
1
2
(
"
Q
2
, 0, 0,
"
Q
2
)
get very large, but their ratio x = Q
2
/2ν remains constant,
ν
M
N
=
q
· P
M
N
= βγ
"
Q
2
=
Q
2
2M
N
x
⇒βγ =
ν/M
N
"
Q
2
=
"
Q
2
2M
N
x
(9)
must hold. Since
"
Q
2
M
N
and x ≤ 1, equation (9) can be fulfilled only for
β ≈ 1, γ 1. Hence (7) becomes
P
µ
≈ (
˜
P, 0, 0, −
˜
P), where
˜
P = βγM
N
=
"
Q
2
2x
. (10)
This is (3.62). In the Breit system the nucleon (and with it all partons) and the
photon move in the z direction towards each other. In the final state the scattered
parton carries the momentum (x denotes the initial momentum fraction of the
parton, i.e., P
i
µ
= xP
µ
)
P
f
µ
= xP
µ
+q
µ
= x(
˜
P, 0, 0, −
˜
P) +q
µ
=
"
Q
2
2
, 0, 0, −
"
Q
2
2
+q
µ
=
"
Q
2
2
, 0, 0,
"
Q
2
2
. (11)
Obviously the spatial momentum of the parton is flipped to its opposite direction
by the reaction (see Fig. 3.9). In the Breit system the parton is simply reflected.
We shall come back to this in Example 3.8.
EXERCISE
3.7 The Scattering Tensor for Scalar Particles
Problem. Repeat the steps leading to (3.18) for scalar particles.
Solution. We start with (3.6). In the case of scalar particles all terms containing
γ matrices vanish:
Γ
µ
= BP
µ
+CP
µ
. (1)
The requirement of gauge invariance, (3.8), then yields
q
µ
Γ
µ
=(P
µ
− P
µ
)Γ
µ
= B(P
µ
− P
µ
)P
µ
+C(P
µ
− P
µ
)P
µ
= BP
µ
P
µ
−CP
µ
P
µ
=(B −C)M
2
N
= 0 ⇒ C = B , (2)

114 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.7
Γ
µ
= B(P
µ
+ P
µ
). (3)
This is rewritten by replacing P
µ
by P
µ
and q
µ
:
Γ
µ
= B(P
µ
+q
µ
+ P
µ
)
=2B
P
µ
+
1
2
q
µ
=2B
P
µ
−q
µ
−q
2
/2
q
2
=2
P
µ
−q
µ
P ·q
q
2
B(Q
2
), (4)
where relation (3.7) has been employed in the last step. For a free scalar field one
simply has
u
∗
(P)u(P) = const . (5)
Therefore W
µν
follows directly from Γ
µ
as
W
µν
=const ×Γ
µ
Γ
ν
=const ×
P
µ
−q
µ
P ·q
q
2
P
ν
−q
ν
P ·q
q
2
B
2
(Q
2
). (6)
Up to now we have considered the elastic process. To obtain the equation equiva-
lent to (6) for the inclusive inelastic case, we again have to replace B
2
(Q
2
) by
B
2
(Q
2
,ν)=: W
2
(Q
2
,ν).
W
µν
=const ×
P
µ
−q
µ
P ·q
q
2
P
ν
−q
ν
P ·q
q
2
W
2
(Q
2
,ν) . (7)
Comparing this result with (3.18) shows that there is only a W
2
function and no
W
1
function for scalar particles. Consequently (3.66) then becomes
d
2
σ
dxdy
=
4πsα
2
Q
4
(1 − y)F
2
(Q
2
, x), (8)
with a corresponding structure function F
2
(Q
2
, x). Here, in the last step, the
term xyM
2
N
/s has been neglected for large s.

3.2 The Description of Scattering Reactions 115
EXAMPLE
3.8 Photon–Nucleon Scattering Cross Sections
for Scalar and Transverse Photon Polarization
Electron–nucleon scattering can be viewed as the scattering of high-energy trans-
verse and longitudinal photons off the nucleon. These photons are created in the
scattering process of the electron. Note that these are virtual photons, i.e. they are
not on the mass shell. These photons have the effective mass q
2
=q
µ
q
µ
=−Q
2
and carry the energy ν = M
N
(E
−E). Thus their energy is exactly given by the
inelasticity ν known from (3.19) and (3.28). For scalar as well as for transverse
polarized photons the spin 4-vector is perpendicular to the photon momentum.
With
q
µ
=(ν/M
N
, 0, 0, q
3
), Q
2
=−q
µ
q
µ
=q
3
−
ν
2
M
2
N
(1)
the spin unit vectors can, in the laboratory system, be chosen as follows. For the
transverse case
ε
1,µ
= (0, 1, 0, 0), ε
2,µ
= (0, 0, 1, 0). (2)
Scalar polarization is defined by
ε
0,µ
= (q
3
, 0, 0,ν/M
N
)
1
"
Q
2
. (3)
Clearly
ε
λ,µ
q
µ
= 0(4)
and
ε
0,µ
ε
µ
0
= 1 ,
ε
1,µ
ε
µ
1
=−1 ,
ε
2,µ
ε
µ
2
=−1 ,
or simply
ε
λ,µ
ε
λ,µ
= 1forλ = 0, 1, 2 . (5)
In the case of photon–nucleon scattering we get
σ(γ N →X) = const ×ε
λ,µ
ε
λ,ν
W
µν
(6)
for the inclusive cross section, where ε
λ,µ
denotes the polarization vector of the
incoming photon. By means of (3.18) and
P
µ
= (M
N
, 0, 0, 0), (7)
Fig. 3.10. Photon-nucleon
vertex

116 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.8
it follows from the general structure (6) and from (2) that the cross section for
transverse photons is proportional to W
11
, W
22
, W
12
,andW
21
. By inspection
of (3.18) it is clear that only W
11
and W
22
contribute and both are proportional
to W
1
Q
2
,ν
. Therefore
σ
T
(γ N →X) = const ×W
1
Q
2
,ν
(8)
can be derived in the laboratory system for transversely polarized photons. For
scalar photons one has
ε
0
· P = q
3
M
N
1
"
Q
2
,
ε
0
·q =
ν
M
N
q
3
−q
3
ν
M
N
=0 ,
ε
0
·ε
0
=
q
2
3
−
ν
2
M
2
N
1
Q
2
=
−Q
2
Q
2
=−1 .
Therefore
σ
S
(γ N →X)
= const ×
⎡
⎣
−q
2
3
+ν
2
/M
2
N
Q
2
+0
W
1
Q
2
,ν
+
M
N
q
3
"
Q
2
2
W
2
Q
2
,ν
M
2
N
⎤
⎦
= const ×
'
−W
1
Q
2
,ν
+
q
2
3
Q
2
W
2
Q
2
,ν
(
. (9)
Inserting (3.43) now yields
σ
T
(γ N →X) = const ×
1
M
N
F
eN
1
Q
2
, x
,
σ
S
(γ N →X) = const ×
1
M
N
'
−F
eN
1
Q
2
,ν
+
q
2
3
M
2
N
Q
2
ν
F
eN
2
Q
2
,ν
(
.
(10)
Because
Q
2
=q
2
3
−q
2
0
=q
2
3
−ν
2
/M
2
N
, (11)
the factor in front of F
eN
2
Q
2
,ν
can be simplified to
q
2
3
M
2
N
Q
2
ν
=
Q
2
+ν
2
M
2
N
Q
2
ν
=
M
2
N
ν
+
1
2x
, (12)
with x = Q
2
/2ν, as usual. In the scaling region ν M
2
N
we therefore obtain
σ
T
(γ N →X)|
ν
2
,Q
2
(1GeV)
2
=const ×
1
M
N
F
eN
1
(x), (13)
σ
S
(γ N →X)|
ν
2
,Q
2
(1GeV)
2
=const ×
1
M
N
1
2x
F
eN
2
(x) −F
eN
1
(x)
. (14)
