Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

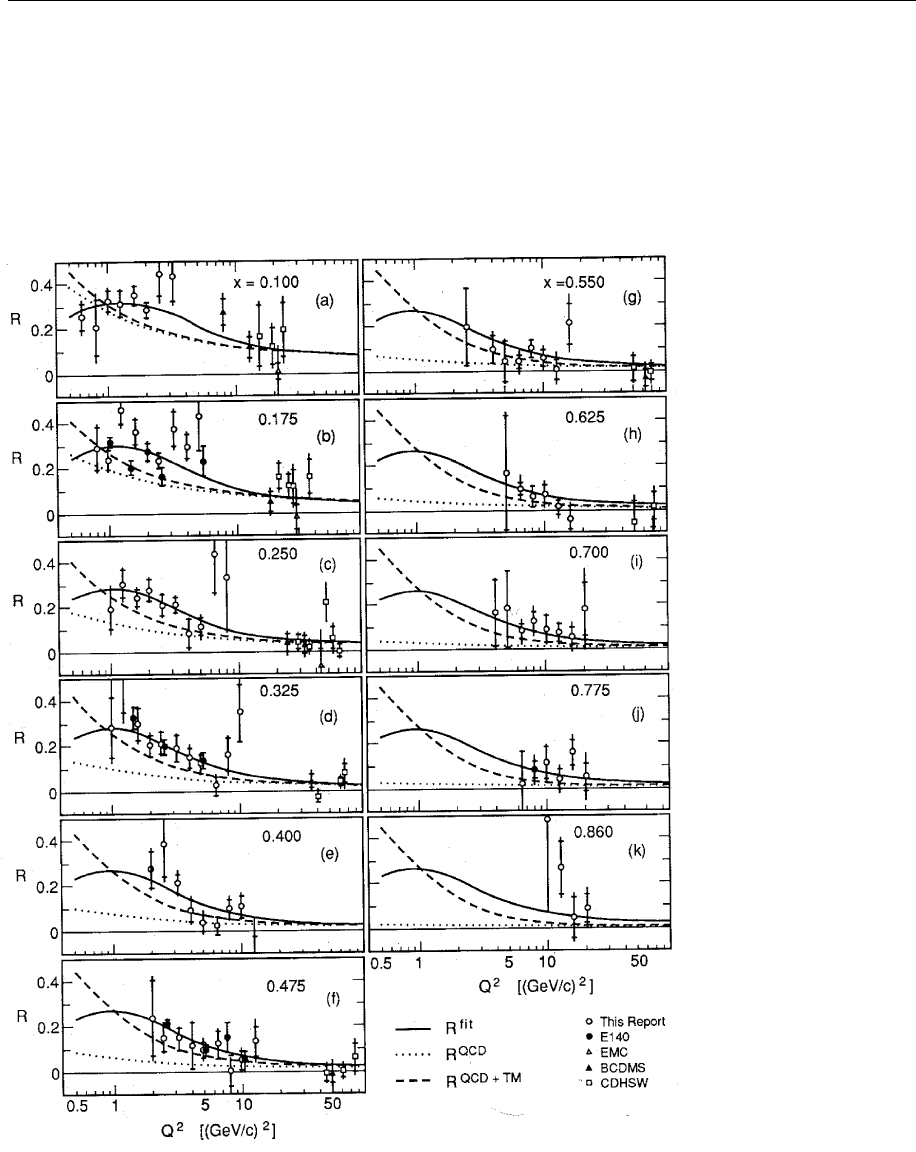
3.2 The Description of Scattering Reactions 117
Because of the Callan–Gross relation (3.83), σ
S
should therefore vanish. See
Fig. 3.11.
In fact, Fig. 3.6 was obtained by analyzing photon–nucleon scattering.
It should be noted that on the other hand F
1
(x) = 0 holds for scalar particles (see
Exercise 3.7). We would therefore expect σ
T
/σ
S
→0 for scalar partons. But this
contradicts experimental observations, i.e., all models that represent the charged
constituents of the nucleon by scalar particles are nonphysical. These results can
easily be understood within the Breit system. To that end one only has to re-
Fig. 3.11a–k. Measured
values of R(x, Q
2
) =σ
s
/σ
T
as analyzed by Whitlow
et al. (Phys. Lett. B 250,
193 (1990)). The dotted and
dashed curves represent per-
turbative QCD predictions
with and without target mass
corrections. The solid line
represents a best-fit model to
all available data
Example 3.8
118 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.8
member that for transverse photon polarization the spin is either parallel to the
direction of motion or opposite to it (right or left circular polarization). More
precisely, this means that
ε
+
µ
=−(ε
1,µ
+iε
2,µ
)
1
√
2
, S·q =+|q| , (15)
and
ε
−
µ
=(ε
1,µ
−iε
2,µ
)
1
√
2
, S·q =−|q| . (16)
Here S denotes the photon spin. According to Fig. 3.11 the partons do not carry
angular momentum and spin and consequently the photon can only be absorbed
by the parton if the spin component in the z direction of the latter particle is
changed by 1. But this is impossible for scalar particles and leads to σ
T
=0.
Massless spin-
1
2
particles, however, encounter a completely different situation.
For these particles the spin component parallel to the direction of motion can
only assume the values +1/2and−1/2. The corresponding spin states are
known as positive and negative helicity or as right-handed and left-handed par-
ticles. Helicity states are defined by the projection operator
(
1 ±γ
5
)
/2 applied
to the wave function (spinor), left-handed and right-handed states by the projec-
tion of the spin onto the momentum axis. For ultrarelativistic particles, positive
helicity corresponds to right-handed particles, that is the spin points in the di-
rection of motion, and negative helicity corresponds to the spin pointing in the
opposite direction. The vector γ
µ
conserves the helicity, i.e., left-handed parti-
cles, for example, couple only to other left-handed particles (see Sect. 4.1). Since
the direction of motion of a parton is changed into its opposite in the Breit sys-
tem, the spin must consequently be flipped at the same time (for sufficiently fast
partons, i.e., for sufficiently large Q
2
). Therefore spin-
1
2
partons are only able to
absorb a photon if S
z
is equal to ±1, i.e., if the photon is transverse. In this case
σ
T
is nonzero (see Fig. 3.11).
Scalar photons (the Coulomb-field, for example, consists of such photons)
have zero spin projection, i.e., here σ
S
=0forspin-
1
2
partons and σ
S
= 0for
spin-0 partons, which is the opposite of the situation encountered by their
transverse counterparts.
EXAMPLE
3.9 A Simple Model Calculation for the Structure Functions
of Electron–Nucleon Scattering
As already stated, the structure functions W
1
Q
2
,ν
and W
2
Q
2
,ν
of (3.36)
can be derived from any microscopic model. This procedure, however, is quite
cumbersome, but it allows predictions for values of Q
2
and ν
2
smaller than
(1GeV)
2
, i.e., for values beyond the scaling region. If we are interested only in
3.2 The Description of Scattering Reactions 119
the restricted information provided by F
2
(x), then there is an easier way. In this
case we can start directly from (3.81):
F
eN
2
(x) =
i
f
i
(x)q
2
i
x . (1)
The only input needed is the functions f
i
(x), i.e., the probabilities that the parton
with index i carries a fraction x of the total momentum. We are going to evelu-
ate these probabilities in an extremely simple model by making the following
assumptions:
(1) The nucleon consists of quarks.
(2) The wave functions of up and down quarks are identical, which yields
F
eN
2
(x) =
i
q
2
i
f(x)x . (2)
Averaging the structure function over the proton and neutron gives
F
eN
2
(x) =
1
2
F
ep
2
(x) +F
en
2
(x)
=
3
2
'
2
3
2
+
1
3
2
(
f(x)x
=
5
6
f(x)x . (3)
(3) We employ Gaussian distributions for the internal wave functions in position
space, i.e., we set
Ψ
P
(r, s) =
α
2
3π
2
exp
)
α
2
'
1
2
r
2
−2
P ·r
M
2
+
2
3
s
2
−2
P ·s
M
2
(*
(4)
with four-dimensional (i.e. space–time) Jacobi coordinates
r
µ
=(z
2
−z
3
)
µ
,
s
µ
=
z
1
−
1
2
(z
2
−z
3
)
µ
,
=
1
2
(2z
1
−z
2
−z
3
)
µ
. (5)
Here Ψ
P
(r, s) is the three-quark wave function, while the quark positions and
the proton momentum are denoted by the four-vectors z
1
, z
2
, z
3
,andP
µ
,
respectively.
Example 3.9

120 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.9
Statements 1 and 2 are quite clear but the wave function (4) needs further
explanation. First one has to take into account that the center-of-mass motion
separates, i.e., the center-of-mass coordinate Z
µ
=
1
3
(z
1
+z
2
+z
3
)
µ
must not
occur in (4). Then the differences between the quark coordinates are assumed
to be Gaussian distributed. This can be archieved by employing Gaussian distri-
butions for r and s. The structure of (4) can be better understood by writing a part
of the exponent in its explicit form:
r
2
2
+
2s
2
3
=
1
6
3z
2
2
−6z
2
z
3
+3z
2
3
+4z
2
1
+z
2
2
+z
2
3
−4z
1
z
2
−4z
1
z
3
+2z
2
z
3
=
2
3
z
2
1
+z
2
2
+z
2
3
−z
1
z
2
−z
2
z
3
−z
3
z
2
=
1
3
(z
1
−z
2
)
2
+(z
1
−z
3
)
2
+(z
2
−z
3
)
2
. (6)
We could think of employing spatial Gaussians only and plane waves with re-
spect to the time coordinate. This represents the completely noninteracting case
and ensures energy conservation at any time t. Consequently each quark carries
exactly one third of the total energy. In an interacting theory the energy of every
parton is a function of time and varies in general around a mean value. One can
simulate this effect by using another Gaussian like
exp
−
α
4
r
2
0
+r
2
, (7)
which is clearly a useful assumption. Note the bold letter r in the exponen-
tial, which indicates the three-vector r. Expression (7) ensures that the three
quarks populate neighboring positions at neighboring times and therefore de-
scribe a bound state. Unfortunately a function that is localized in space and time
is not Lorentz invariant. A Lorentz-invariant wave function would be of the form
exp(αr
2
/4) = exp(α(r
2
0
−
r
2
)/4). In order to restore Lorentz invariance in (7) we
now use the fact that the proton momentum in the rest system is simply
P
µ
=(M, 0, 0, 0). (8)
We therefore obtain in the rest system
exp
−
α
4
r
2
0
+r
2
= exp
α
4
r
2
−
2
M
2
(P ·r)
2
. (9)
The same holds for the s-dependent part of the wave function (4). The total wave
function has been normalized in such a way that
d
4
r d
4
s Ψ
2
P
(r, s) = 1 (10)
holds. Starting with (4) we now determine the mean square charge radius of the
proton, which is given by (P
µ
= (M, 0, 0, 0)):
r
2
c
=
d
4
r d
4
s
i
q
i
(z
i
−Z)
2
Ψ
2
P
(r, s). (11)
3.2 The Description of Scattering Reactions 121
With the help of the center-of-mass coordinate Z =
1
3
(z
1
+z
2
+z
3
) we get
i
q
i
(z
i
−Z)
2
=−
1
3
(z
1
−Z)
2
+
2
3
(z
2
−Z)
2
+
2
3
(z
3
−Z)
2
=−
1
27
(2z
1
−z
2
−z
3
)
2
+
2
27
(2z
2
−z
1
−z
3
)
2
+
2
27
(2z
3
−z
1
−z
2
)
2
=
1
27
−4z
2
1
−z
2
2
−z
2
3
+4z
1
·z
2
+4z
1
·z
3
−2z
2
·z
3
+2z
2
1
+8z
2
2
+2z
2
3
−8z
2
·z
1
−8z
2
·z
3
+4z
1
·z
3
+2z
2
1
+2z
2
2
+8z
2
3
−8z
3
·z
1
−8z
3
·z
2
+4z
1
·z
2
=
1
27
9z
2
2
+9z
2
3
−18z
2
·z
3
=
1
3
r
2
. (12)
In the center-of-mass system this yields
r
2
c
=
1
3
α
2
3π
2
2
d
4
s exp
−
2α
3
s
2
0
+ s
2
dr
0
d
3
r e
−
α
2
r
2
0
e
−
α
2
r
2
r
2
=
α
√
α
6π
√
3π
4π
∞
0
drr
4
e
−
α
2
r
2
=
1
α
. (13)
This can be used to fix the yet undetermined parameter α in the wave function Ψ
P
of (4). Thus we have to insert the value
α =
1
r
2
c
≈1.5fm
−2
(14)
for α. Up to now we have described the internal structure of the proton with the
ansatz (4). The free proton moves, however, with the total momentum P. Thus,
from (4) we then get for the total proton wave function
Ψ
P
(r, s, Z) =
α
2
3π
2
e
−iP·Z
√
VT
exp
)
α
2
'
1
2
r
2
−2
P ·r
M
2
+
2
3
s
2
−2
P ·s
M
2
(*
(15)
with the normalization
d
4
r d
4
s d
4
Z Ψ
†
P
(r, s, Z)Ψ
P
(r, s, Z) = 1 . (16)
Here, VT denotes the integration volume for Z.
Example 3.9
122 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.9
In order to understand the following, note that the one-particle Wigner
function
f(Z, p) :=
d
4
v
(2π)
4
e
−i p
µ
v
µ
Ψ
†
Z
µ
−
1
2
v
µ
Ψ
Z
µ
+
1
2
v
µ
(17)
yields the probability for finding a particle at a position Z
µ
with a momen-
tum P
µ
.HereΨ(x) denotes the one-particle wave function. Now it is easy to
evaluate from (15) the distribution function f(x) of, for example, the first parton
(at position z
1µ
in space–time):
f
1
(z
1
, p
µ
) = N
d
4
v e
−i p
µ
v
µ
d
4
z
2
d
4
z
3
× Ψ
†
P
(r, s, Z)
z
1,µ
→s
1,µ
+
1
2
v
µ
Ψ
P
(r, s, Z)
|
z
1,µ
→s
1,µ
−
1
2
v
µ
. (18)
The normalization constant N is determined later. The probability of finding
a parton with momentum p = xP at position z
1
is
f
1
(x) =
d
4
z
1
f
1
(z
1
, xP)
= N
d
4
v e
−iP
µ
v
µ
x
d
4
z
1
d
4
z
2
d
4
z
3
×Ψ
†
P
r, s +
1
2
v, Z +
1
6
v
Ψ
P
r, s −
1
2
v, Z −
1
6
v
= N
d
4
v e
−iP
µ
v
µ
x−
1
3
d
4
z
1
d
4
z
2
d
4
z
3
α
4
9π
4
VT
×exp
)
α
'
1
2
r
2
−2
P ·r
M
2
+
2
3
s
2
−2
P ·s
M
2
+
1
6
v
2
−2
P ·v
M
2
(*
. (19)
The integration over z
1
, z
2
,andz
3
is now transformed into one over r, s,andz.
The corresponding functional determinant is
∂(r, s, z)
∂(z
1
, z
2
, z
3
)
=
01−1
1 −
1
2
1
2
1
3
1
3
1
3
=−
1
3
. (20)
Because we have four-dimensional integrals, the determinant occurs four times,
i.e. we get the factor (−3)
4
. By employing (16) we can reduce (19) to
f
1
(x) = N
d
4
v exp
−iP
µ
v
µ
x −
1
3
exp
α
6
'
v
2
−2
P ·v
M
2
(
,
(21)

3.2 The Description of Scattering Reactions 123
where N
= 3
4
N. Since this expression is Lorentz invariant, we can again
evaluate it in the rest system:
f
1
(x) = N
d
4
v exp
−iMv
0
x −
1
3
exp
−
α
6
v
2
0
+v
2
= N
6π
α
3/2
dv
0
exp
−
α
6
v
0
+i
3M
α
x −
1
3
2
exp
−
3M
2
2α
x −
1
3
2
= N
6π
α
2
exp
−
3M
2
2α
x −
1
3
2
. (22)
Here the standard formula
+
∞
−∞
e
−x
2
dx =
√
π has been employed. Now we rec-
ognize the following. For the simple quark model considered here the distribu-
tion functions are peaked around x = 1/3. This can immediately be understood,
because it only means that each quark carries on average one third of the to-
tal momentum. Figure 3.12 shows, however, that the experimentally observed
distribution functions increase monotonically for small values of x. Obviously
every charged particle has less momentum than one would expect from our sim-
ple quark model. Consequently there must be more partons in a nucleon than
those three, which correspond to valence quarks.
Because of the approximations leading to (22), x can become larger than 1
and even assume negative values. In these cases, however, f(x) is more or
less zero. These difficulties are mainly due to assumption (4), which contains
arbitrarily large parton momenta (being the Fourier transform of a Gaussian
distribution: indeed, (22) is again a Gaussian). Consequently f
1
(x) should be
normalized according to
1 =
∞
−∞
f
1
(x)dx = N
6π
α
2
!
π2α
3M
2
, (23)
Fig. 3.12. The experimen-
tally observed F
2
structure
function of deep inelastic
electron–nucleon scattering
Example 3.9

124 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.9
Fig. 3.13. Comparison of
the experimentally observed
F
2
structure function of deep
inelastic electron–nucleon
scattering with our simple
model calculation
which gives
f
1
(x) =
6
3M
2
2πα
exp
−
3M
2
2α
x −
1
3
2
. (24)
The function (3),
F
eN
2
(x) =
1
2
F
ep
2
(x) +F
en
2
(x)
= 3 ×
5
18
× f
1
(x)x , (25)
obtained in this way is depicted in Fig. 3.13. The qualitative deviation from ex-
perimental results is considerable. The failure of the model, however, yields
valuable information about specific features of the quark–quark interaction,
which help to obtain better results. In addition note that
3
∞
−∞
xf
1
(x)dx = 3
∞
−∞
x +
1
3
6
3M
2
2πα
exp
−
3M
2
2α
x
2
dx
= 3
0 +
1
3
=1(26)
holds. Therefore the three quarks together carry the whole proton momentum.
This result is not surprising. It is inherently built into this naive model. In other
words: Owing to our assumptions, this must obviously be true, and therefore (26)
represents a test of our calculation.
In the next section we shall discuss a more refined model for the nucleon, i.e.
the MIT bag model. Later, in Sect. 5.6, we shall see what the structure functions
of this model look like. In fact they do not agree much better with the data than

3.3 The MIT Bag Model 125
our present results. We shall then also see how by adding ad hoc the Q
2
evolu-
tion from QCD the confrontation of theory with experiment improves and the
agreement becomes much more acceptable.
3.3 The MIT Bag Model
Before turning in the following chapters to today’s prevailing theory of quark–
quark interaction, we shall first discuss a specific ‘bag model’, the MIT bag
model, in more detail.
10
Since no free quarks have been observed experimen-
tally, one imagines that the quarks are tightly confined inside the hadrons. Inside
of this confinement volume they behave mainly as free particles. All bag models
must be regarded as pure phenomenology. It is at present unclear how strong any
relationships between such models and QCD are. Should the confinement prob-
lem one day be solved from the QCD equations (which we shall discuss in the
next chapter), it might turn out that the model assumptions of the MIT bag are
unphysical. Besides this basic problem, there are also difficulties inherent to the
MIT bag model. The rigid boundary condition can lead to spurious motions, e.g.,
oscillations of all quarks with respect to the bag, and it is not Lorentz invariant.
These disadvantages are set off by the great advantage that nearly all inter-
esting processes and quantities can be calculated in a bag-model framework.
Sometimes there are quite far-reaching approximations involved, but in to-
tal these recipes allow for quite a good phenomenological understanding of
subhadronic physics. This might be found more satisfactory than a strictly for-
mal theory of quark–quark interaction which fails to predict many physically
interesting quantities owing to mathematical difficulties (insufficiencies).
We shall now formulate the MIT bag model. Start from the fact that the
quark–quark interaction makes it impossible to separate colored quarks. This
is most easily implemented by specifying some surface and demanding that
the color current through it vanishes. This color current is analogous to the
electromagnetic current and reads
ˆ
J
α
µ
= (q
r
, q
b
, q
g
)λ
α
γ
µ
⎛
⎝
q
r
q
b
q
g
⎞
⎠
(3.94)
with the eight color SU(3) matrices λ
a
. The subscripts stand for the three colors
(‘red’, ‘blue’, and ‘green’). Let the chosen surface be characterized by a normal
10
See also W. Greiner and B. Müller: Quantum Mechanics – Symmetries, 2nd ed.,
(Springer, Berlin, Heidelberg 1994), P. Hasenfratz, J. Kuti, Phys. Rep. 40 C,75
(1978).

126 3. Scattering Reactions and the Internal Structure of Baryons
vector n
µ
. Then the desired condition can be written as
n
µ
·
ˆ
J
α
µ
=0
surface
,α= 1, 2, 3, ..., 8 . (3.95)
By introducing a four-dimensional normal vector we have reached a covariant
form, but this does not correspond to a general covariance of the model because
we must still specify the bag surface. Indeed we restrict ourselves to purely
spatial surfaces, i.e., n
µ
→n :
−n · J
α
R=R (θ,ϕ)
= 0 . (3.96)
To simplify (3.96) further, color independence is demanded of the internal quark
wave function, i.e., q
i
(x) = q(x), i =r, b, g. In this way we obtain the ‘quadratic
bag boundary condition’
n ·
qγ q
R=R (θ,ϕ)
=0 . (3.97)
The expression n ·γ has the property that its square is the negative unit matrix:
(n ·γ )
2
=n
i
n
j
1
2
(γ
i
γ
j
+γ
j
γ
i
) =−n
i
n
i
11 =−(n)
2
·11 =−11 . (3.98)
Its eigenvalues are accordingly ±i. Now, each quark state can be expanded into
the corresponding eigenvectors, and, how wonderful, (3.97) is satisfied for just
these eigenstates. This can be seen in the following way: From
n ·γ q
+
= iq
+
(3.99)
it follows by Hermitian conjugation that
(q
†
+
n ·γ
†
)γ
0
=−iq
+
,
⇒
q
+
n ·γ =−iq
+
. (3.100)
If one multiplies (3.99) by
q
+
from the left and (3.100) by q
+
from the right and
adds both equations, then it follows that
q
+
n ·γ q
+
= 0 (3.101)
and similarly for the eigenvalue −i. By restricting ourselves to eigenvectors of
n ·γ , we can thus always guarantee that (3.97) is satisfied. In other words, instead
of solving (3.97), which is bilinear in the quark wave function q(x), one may
solve the much easier linear equations
n ·γ q =±iq . (3.102)
The disadvantage of this procedure is that other solutions of (3.97) that are not
eigenvectors of n ·γ are excluded in this way.
