Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


3.3 The MIT Bag Model 147
Thechargeoperator
ˆ
Qr
2
acts on one quark at a time. For the proton it can be
replaced by
ˆ
Qr
2
→ Q
1
r
2
1
+Q
2
r
2
2
+Q
3
r
2
3
. (3)
Equation (1) then becomes
r
2
ch
=
1
e
d
3
r
1
d
3
r
2
d
3
r
3
1
6
2u
↑
(1)u
↑
(2)d
↓
(3)
−u
↑
(1)d
↑
(2)u
↓
(3) −d
↑
(1)u
↑
(2)u
↓
(3)
†
×(Q
1
r
2
1
+Q
2
r
2
2
+Q
3
r
2
3
)
2u
↑
(1)u
↑
(2)d
↓
(3)
−u
↑
(1)d
↑
(2)u
↓
(3) −d
↑
(1)u
↑
(2)u
↓
(3)
. (4)
All quarks are assumed to be massless and in the same state (namely the 1s state),
i.e., we do not distinguish between up and down quarks. Therefore r
2
2
and r
2
3
can
be replaced in the integrand by r
2
1
:
Q
1
r
2
1
+Q
2
r
2
2
+Q
3
r
2
3
→(Q
1
+Q
2
+Q
3
)r
2
1
= er
2
1
. (5)
Now the integrals over r
2
and r
3
can easily be evaluated by using the orthogo-
nality relations
d
3
r
2
q
s
†
(2) q
s
(2) = δ
qq
δ
ss
,
#
q, q
= u, d
s, s
=↑, ↓
. (6)
r
2
ch
=
d
3
r
1
r
2
1
1
6
4u
↑†
(1)u
↑
(1) +u
↑†
(1)u
↑
(1) +d
↑†
(1)d
↑
(1)
. (7)
Owing to the assumption made above, the wave functions of u and d yield the
same contributions, and (7) simplifies to
r
2
ch
=
dΩ
1
dr
1
r
4
1
u
↑†
(1)u
↑
(1). (8)
Now we insert the explicit form of the wave function (3.128) and skip the index 1
in the remaining calculation:
r
2
ch
= N
2
dr
dΩr
4
j
2
0
(Er)χ
1
2
†
1
(Ω) χ
1
2
1
(Ω) + j
2
1
(Er)χ
1
2
†
−1
(Ω) χ
1
2
−1
(Ω)
.
(9)
Because of the orthogonality of the spherical spinors and because of (3.142), (9)
assumes the form
r
2
ch
=
ER
2R
3
(ER−1) j
2
0
(ER)
R
0
dr r
4
j
2
0
(Er) + j
2
1
(Er)
. (10)
Exercise 3.13
148 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.13
The remaining integral can again be evaluated by means of the recursion
relations or simply by inserting the explicit expressions
j
0
(r) =
sin z
z
,
j
1
(z) =
sin z
z
2
−
cos z
z
. (11)
Hence
r
2
ch
=
ER(ER)
2
2R
3
(ER−1) sin
2
(ER)
×
R
0
drr
4
sin
2
(Er)
E
4
r
4
−2
sin(Er) cos(Er)
E
3
r
3
+
1
E
2
r
2
=
1
2E(ER−1) sin
2
(ER)
×
−r sin
2
(Er) +r −
1
E
sin(Er) cos(Er) +
1
3
r
3
E
2
R
0
. (12)
The boundary condition
j
0
(ER) = j
1
(ER)
⇒ ERcos(ER) =(1 −ER) sin(ER) (13)
simplifies (12) to give
r
2
ch
=
1
2E(ER−1) sin
2
(ER)
×
1
E
(1 − ER) sin(ER) cos(ER) −
1
E
sin(ER) cos(ER) +
1
3
R
3
E
2
=
−ERsin(ER) cos(ER) +
1
3
R
3
E
3
2E
2
(ER−1) sin
2
(ER)
=0.53 R
2
. (14)
In the last step we have inserted the numerical value for ER, which, according
to (3.131) is equal to 2.0428.

3.3 The MIT Bag Model 149
EXERCISE
3.14 The Magnetic Moment of the Proton
Problem. Evaluate the right-hand side of (3.158) with the help of the wave
functions (3.153) and (3.128).
Solution. The static magnetic moment is defined as
m =
1
2
r × j(r)d
3
r . (1)
Using the definition of the electromagnetic current of quark i,
j
µ
i
= Q
i
¯
q
i
γ
µ
q
i
, (2)
we get for the spatial component
1
2
r × j
i
=
Q
i
2
¯
q
i
(r ×γ )q
i
=
Q
i
2
q
†
i
(r ×α)q
i
, (3)
where γ
0
γ = α, and therefore the operator of the magnetic moment, is
Q
i
2
(r ×α). (4)
Since the SU(6) wave function of the proton is symmetric under permutations of
the indices 1, 2, and 3, we have
Ψ
†
p
ˆ
Q
1
2
ˆ
r
1
×
ˆ
α
1
Ψ
p
d
3
r
1
d
3
r
2
d
3
r
3
=
Ψ
†
p
ˆ
Q
2
2
ˆ
r
2
×
ˆ
α
2
Ψ
p
d
3
r
1
d
3
r
2
d
3
r
3
=
Ψ
†
p
ˆ
Q
3
2
ˆ
r
3
×
ˆ
α
3
Ψ
p
d
3
r
1
d
3
r
2
d
3
r
3
. (5)
Therefore (3.158) can in a first step be simplified to
µ
p
= 3
d
3
r
1
d
3
r
2
d
3
r
3
Ψ
†
p
ˆ
Q
1
2
ˆ
r
1
×
ˆ
α
1
Ψ
p
=
1
6
d
3
r
1
10u
↑
(1)
†
ˆ
Q
1
2
ˆ
r
1
×
ˆ
α
1
u
↑
(1) +2u
↓
(1)
†
ˆ
Q
1
2
ˆ
r
1
×
ˆ
α
1
u
↓
(1)
+4d
↓
(1)
†
ˆ
Q
1
2
ˆ
r
1
×
ˆ
α
1
d
↓
(1) +2d
↑
(1)
†
ˆ
Q
1
2
ˆ
r
1
×
ˆ
α
1
d
↑
(1)
. (6)

150 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.14
Here we have drawn on the orthogonality of the quark wave function
d
3
rq
s
†
q
s
=δ
qq
δ
ss
, q = u, d , s =↑, ↓ . (7)
Next we insert the quark charges and make use of the fact that up and down
quarks are described by the same spatial wave function. In addition we omit the
index 1:
µ
p
=
e
6
d
3
r
10
3
u
↑†
(
ˆ
r ×
ˆ
α)u
↑
+
2
3
u
↓†
(
ˆ
r ×
ˆ
α)u
↓
−
2
3
d
↓†
(
ˆ
r ×
ˆ
α)d
↓
−
1
3
d
↑†
(
ˆ
r ×
ˆ
α)d
↑
=
e
2
d
3
ru
↑†
(
ˆ
r ×
ˆ
α)u
↑
. (8)
In order to evaluate this expression we insert into it (3.128) in the form
u
↑
= N
⎛
⎝
j
0
(Er)χ
1
2
−1
i j
1
(Er)
ˆ
σ
r
χ
1
2
−1
⎞
⎠
(9)
and obtain
µ
p
=
e
2
N
2
R
0
drr
2
dΩ
j
0
(Er)χ
1
2
†
−1
, −i j
1
(Er)χ
1
2
†
−1
ˆ
σ
r
×
0
ˆ
r ×
ˆ
σ
ˆ
r ×
ˆ
σ 0
⎛
⎝
j
0
(Er)χ
1
2
−1
i j
1
(Er)
ˆ
σ
r
χ
1
2
−1
⎞
⎠
=
e
2
N
2
R
0
drr
2
dΩ i j
0
(Er) j
1
(Er)χ
1
2
†
−1
ˆ
r ×
ˆ
σ
ˆ
σ
r
−
ˆ
σ
r
ˆ
r ×
ˆ
σ
χ
1
2
−1
.
(10)
By means of the commutation relations of the σ matrices, the term inside the
brackets simplifies to
ε
ijk
r
j
ˆ
σ
k
,
ˆ
σ
r
=ε
ijk
ˆ
σ
k
,
ˆ
σ
r
j
r
=ε
ijk
2iε
km
ˆ
σ
m
r
j
r
=2i
δ
i
δ
mj
−δ
j
δ
im
r
j
r
ˆ
σ
m
=2ir
i
ˆ
σ ·r −2ir
2
ˆ
σ
i
. (11)

3.3 The MIT Bag Model 151
Hence
µ
p
=
e
2
N
2
R
0
d rr
2
dΩ i j
0
(Er) j
1
(Er)
1
4π
(
10
)
2irσ
r
−2irσ
1
0
=
eN
2
4π
R
0
d rr
3
j
0
(Er) j
1
(Er)
dΩ
⎡
⎣
e
3
−cos θ
⎛
⎝
sin θ cos φ
sin θ sin φ
cos θ
⎞
⎠
⎤
⎦
,
(12)
wherewehaveused
(σ
j
)
11
=δ
j3
(13)
and
σ ·
r
r
11
=
r
3
r
=cos θ. (14)
Now we can easily perform the φ, θ,andr integrations:
µ
p
=
eN
2
2
e
3
R
0
drr
3
j
0
(Er) j
1
(Er)
1
−1
dcosθ
1 −cos
2
θ
= e
3
2
3
N
2
e
R
0
drr
3
sin(Er)
Er
sin(Er)
E
2
r
2
−
cos(Er)
Er
= e
3
2
3
N
2
E
3
e
−
r
2
sin
2
(Er) −
3
4E
sin(Er) cos(Er) +
3
4
r
R
0
= e
3
2
3
N
2
E
4
e
−
1
2
ω sin
2
ω −
3
4
sin ω cos ω +
3
4
ω
. (15)
Here ω = ER. With the boundary condition
ω cos ω = (1 −ω) sin ω (16)
the expression inside the brackets can further be simplified:
−
3
4
ω sin
2
ω +sin ω cos ω −ω
+
1
4
ω sin
2
ω
=−
3
4
sin
2
ω −ω cos ω sin ω +sin ω cos ω −ω
+
1
4
ω sin
2
ω
=−
3
4
sin
2
ω +ω cos
2
ω −ω
+
1
4
ω sin
2
ω
=−
3
4
(1 −ω) sin
2
ω +
1
4
ω sin
2
ω
=
1
4
(4ω −3) sin
2
ω. (17)
Exercise 3.14

152 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.14
Finally we insert N
2
from (3.142)
µ
p
=e
3
ωe
3R
3
(ω −1)
ω
2
sin
2
ω
1
E
4
1
4
(4ω −3) sin
2
ω
=e
3
eR
ω(ω −1)
4ω −3
12
=0.203 eRe
3
(18)
with ω = 2.04.
Clearly µ
p
hastobeparalleltothez direction, because in the spherical bag
model the quantization axis of the angular momentum is the only direction of
special importance.
Since µ
p
defines a direction, this special direction can be chosen to be iden-
tical with the quantization axis mentioned. In units of the nuclear magneton
µ
0
= e/2m
p
the absolute value of the magnetic moment of the proton is (with
R = 1fm)
|µ
p
|
µ
0
=0.203×1fm×2 ×938.28 MeV =1.9 ,
µ
0
=
e
2m
p
. (19)
The value (3.159) differs considerably from the experimental observation
µ
p
(exp) = 2.79 µ
0
. (3.160)
The magnetic moments predicted for the other hadrons are too small as well. The
ratios of these moments, however, are quite well described.
Table 3.3 compares the MIT model results for the charge radii and the
magnetic moments with the corresponding experimental data.
There are other interesting quantities that can be evaluated in the context of
the MIT bag model. One can usually achieve an agreement similar to that for the
masses, charge radii, and magnetic moments. Later we shall discuss at a much
higher technical level the predictions made by the bag model for the proton struc-
ture functions. Let us now summarize the advantages and disadvantages of the
MIT bag model.
Advantages: The MIT bag model provides a phenomenological description of
hadrons that is quantitatively semicorrect and therefore allows for rough esti-
mates for all quantities not yet experimentally observed. One can furthermore
estimate what phenomenological consequences follow from additional quark in-
teractions. For example, the bag model allows us to connect the known weak
interaction of hadrons to the weak interaction of quarks.
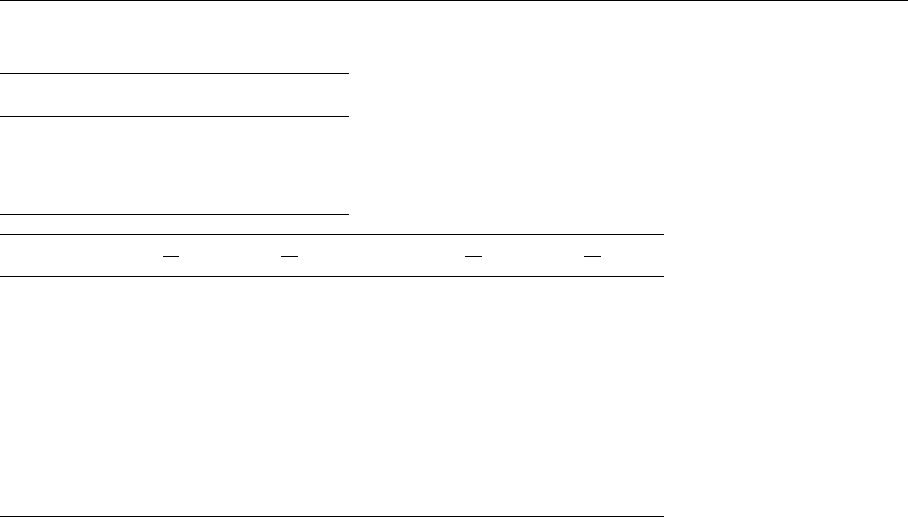
3.3 The MIT Bag Model 153
Table 3.3. Comparison of charge radii and magnetic moments with the cor-
responding results of the MIT bag model
Particles r
2
ch
(exp.) r
2
ch
(theor.)
p0.88 ±0.03 fm 0.73 fm
n −0.12 ±0.01 fm 0
π 0.78 ±0.10 fm 0.5 fm
Particles
µ
µ
0
(exp.)
µ
µ
0
(theor.)
µ
µ
p
(exp.)
µ
µ
p
(theor.)
p 2.793 1.90 −−
n −1.913 −1.27 −0.68 2/3
Λ 0.613±0.004 −0.48 −0.219 ±0.001 −0.26
Σ
+
2.38 ±0.02 1.84 0.85 ±0.01 0.97
Σ
0
− 0.59 − 0.31
Σ
−
−1.14 ±0.05 −0.68 −0.36 ±0.02 −0.36
Ξ
0
−1.25 ±0.014 −1.06 −0.448 ±0.005 −0.56
Ξ
−
−0.69 ±0.04 −0.44 −0.25 ±0.01 −0.23
Disadvantages: The bag model is conceptually unsatisfying. The physical mean-
ing of the specific correction terms is unclear and the model is neither renormal-
izable nor Lorentz invariant. In addition one obtains similarly good results with
completely different approaches (see Sect. 3.1). The basic physical assumptions
of these models, i.e., for the MIT bag the rigid boundary condition and the free
motion of the quarks inside the bag, differ drastically. Therefore at least some of
them should be wrong.

4. Gauge Theories and Quantum-Chromodynamics
Nowadays the common model of quark–quark interactions is an SU(3) gauge
theory in a degree of freedom, arbitrarily called “color”. There are meanwhile
many experimental facts supporting this model, as we shall discuss later in more
detail. It seems by now also to be proven that QCD (quantum chromodynamics)
is able to correctly describe the most pronounced feature of quark–quark interac-
tions, i.e., confinement, and that it will generate, for example, the correct hadron
masses. The results obtained so far are all compatible with the phenomenologi-
cal properties, but in many cases the accuracy of calculations is still rather low.
Typical uncertainties for hadron masses, for example, are 10%. In fact, the gen-
eral acceptance of QCD is based not only on its own achievements, but also
to a large extent on the outstanding success of the gauge theory of weak and
electromagnetic interactions. For this reason we begin with a brief overview of
the Glashow–Salam–Weinberg model. (The Glashow–Salam–Weinberg model
combined with QCD is usually called the standard model). The typical features
of gauge theories are discussed in the context of this specific model.
4.1 The Standard Model: A Typical Gauge Theory
The ideas of local internal symmetries and gauge transformations were intro-
duced quite a long time ago. But the actual reason for developing the modern
schemes for general non-Abelian gauge theories was the lack of a renormalizable
field theory for massive spin-1 particles.
Spin-0 and spin-
1
2
particles are described by the well-known method of field
quantization, employing the Klein–Gordon and the Dirac Lagrangians, respec-
tively. This procedure also applies to massless spin-1 particles, despite some
complications owing to the four-potentials A
µ
not being physical observables.
The theory obtained in this way proved to be excellent, in particular the part
known as quantum electrodynamics. However, a consistent field theory for mas-
sive vector particles, especially a field theory of weak interactions, could not be
formulated. This problem even led some physicists to doubt the whole concept of
local field theories. On the other hand, having overcome that difficulty, quantum
field theory is today considered the correct theory of elementary particles (the
validity of a possible alternative, the so-called “string models”, is still heavily
disputed).

156 4. Gauge Theories and Quantum-Chromodynamics
We shall not analyze the properties of gauge theories in this volume. A deeper
understanding requires a lot of formal knowledge, which we shall present in an-
other book. At this point we restrict ourselves to describing the general structure
of gauge theories and we simply state that all theories built on these principles
are renormalizable.
The standard model contains the well-known electromagnetic interaction.
Here the photon is described by the free Lagrangian
L
0
=−
1
4
F
µν
F
µν
, F
µν
=∂
µ
A
ν
−∂
ν
A
µ
, (4.1)
and its coupling to, for example, the electron via the interaction term
L
int
=Ψ(
ˆ
p
µ
−eA
µ
)γ
µ
Ψ. (4.2)
These equations already include the most basic assumption of quantum field
theory: elementary particles have to be described by local fields and point inter-
actions. As a matter of fact, only the four-potentials A
µ
and not the “physical”
fields E and B can fulfill these requirements. If E and B are regarded as elemen-
tary, then the electromagnetic interaction has to be nonlocal. The best proof of
this is the Aharonov–Bohm effect.
1
The phase of a charged particle’s wave func-
tion is influenced by magnetic fields located in an area where the wave function
itself is zero.
As is well known, Lagrangians (4.1) and (4.2) are invariant under the
transformation
A
ν
(x) → A
ν
(x) = A
ν
(x) +∂
ν
θ(x),
Ψ(x) →Ψ
(x) = e
ieθ(x)
Ψ(x). (4.3)
Equation (4.3) expresses the fact that not all of the four fields A
µ
correspond
to physical degrees of freedom. Physical quantities must not depend on the
arbitrary “gauge angle” θ(x). This requirement leads to relations between the
propagator and the vertex function, for example, which is important to prove the
renormalizability of QED (the so-called Ward identity).
2
From the gauge symmetry of QED we are led directly to that of a general
gauge group by replacing the complex-valued functions A
ν
by matrix functions.
If
ˆ
λ
j
, j = 1, 2,... ,N is a basis in the chosen matrix space, we correspondingly
have
A
ν
(x) →
j
ˆ
λ
j
2
A
j
ν
(x) =:
ˆ
A
ν
(x),
θ(x) →
j
ˆ
λ
j
2
θ
j
(x) =:
ˆ
θ(x). (4.4)
1
See W. Greiner: Quantum Mechanics – Special Chapters, 1st ed., 2nd printing
(Springer, Berlin, Heidelberg, 2001).
2
See W. Greiner and J. Reinhardt: Quantum Electrodynamics, 3rd ed. (Springer, Berlin,
Heidelberg, 2003).
4.1 The Standard Model: A Typical Gauge Theory 157
The specific choice of matrices determines the underlying symmetry group. If
one chooses, for example, traceless Hermitian 3 ×3 matrices, then the trans-
formations
exp
⎛
⎝
−ig
j
ˆ
λ
j
2
θ
j
(x)
⎞
⎠
(4.5)
are nothing other than a three-dimensional representation of the SU(3)
transformations, where we replaced the electron coupling constant −e by
a generalised constant g. On the other hand, it is clear that any other represen-
tation of SU(3) instead of the chosen matrices would also have been possible.
Since the
ˆ
λ matrices in general do not commute, the equations have to be slightly
changed in the case of (4.4) (in addition, in (4.1)–(4.3) we replace e by −g):
L
0
=−
1
4
ˆ
F
a
µν
ˆ
F
a µν
=−
1
2
tr
ˆ
F
µν
ˆ
F
µν
,
ˆ
F
µν
=∂
µ
ˆ
A
ν
−∂
ν
ˆ
A
µ
−ig
ˆ
A
µ
,
ˆ
A
ν
, (4.6)
L
int
= Ψ
ˆ
p
µ
+g
ˆ
A
µ
γ
µ
Ψ, (4.7)
ˆ
A
ν
(x) →
ˆ
A
ν
(x) = e
−ig
ˆ
θ(x)
ˆ
A
ν
(x) +
i
g
∂
ν
e
+ig
ˆ
θ(x)
,
Ψ(x) →Ψ
(x) = e
−ig
ˆ
θ(x)
Ψ(x). (4.8)
Now Ψ(x) must be defined as a vector corresponding to the choice of
ˆ
A
ν
(x).
(In principle Ψ could also be a matrix; then the trace of L
int
would have to
be evaluated. Such cases occur in models trying to unify the electroweak and
strong interaction with a single symmetry group.) The main content of gauge
field theories is contained in the quantized equations (4.6) and (4.7).
With these few remarks we have already formulated the basic ideas of gauge
theories. But, like many others, this particular physical concept can be further
investigated in two different directions. The first is to study the consequences of
(4.6) and (4.7) in more and more detail. The second deals with the basics of these
equations and tries to discover deeper-lying foundations. Persuing the latters we
could, for example, give a general geometric formulation of the principles of
gauge theories. Being geometric, this formulation shows the same structure as
the basic equations in the theory of general relativity. Such a correspondence
gives rise to the hope that the unification of the theory of gravitation and quantum
theory, which deals with all other kinds of interaction, is no longer completely
unlikely. However, it is still not clear whether this correspondence expresses
a real similarity of both theories or whether it just follows from the general-
ity of geometric considerations. Some elements of the geometric formulation
of gauge theories are discussed in Example 4.1. Here we will discuss only the
phenomenological consequences of (4.6) and (4.7).
