Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

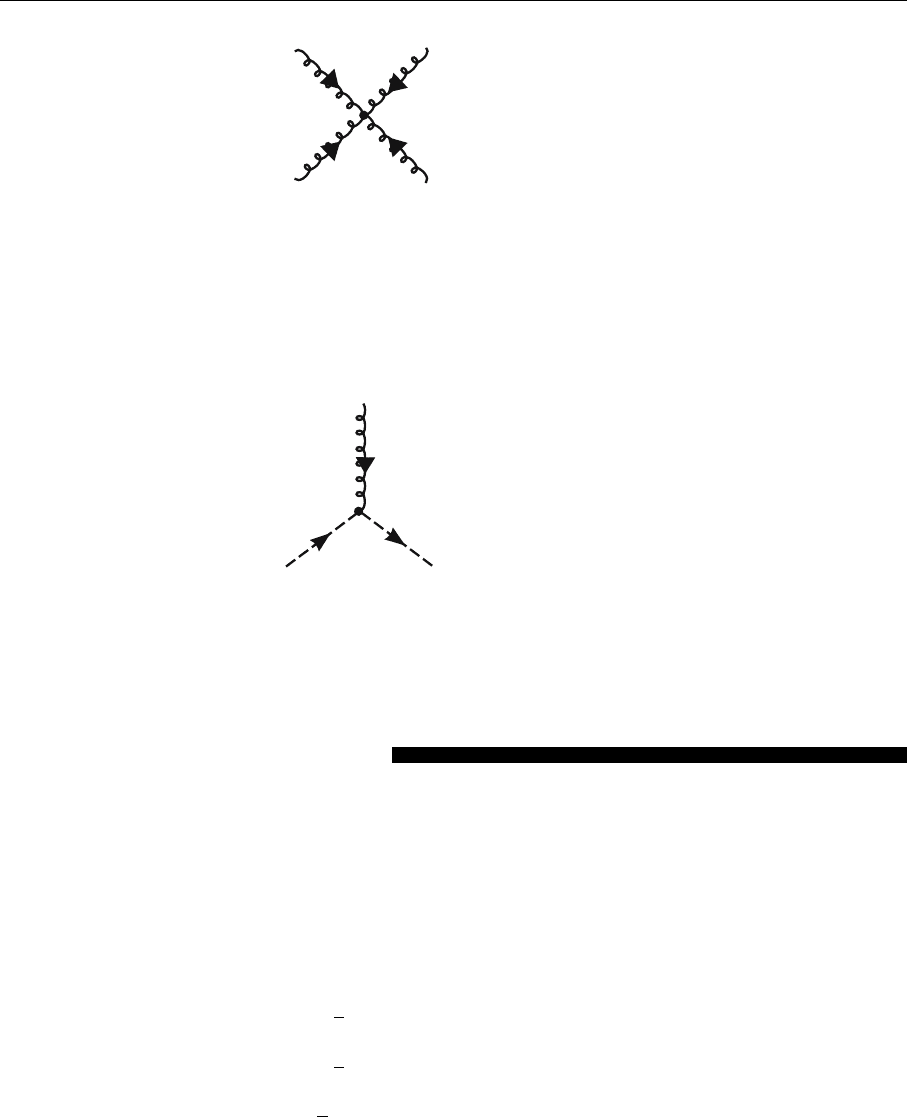
178 4. Gauge Theories and Quantum-Chromodynamics
Example 4.2
ak,,a
1
b
k
,
,
b
2
d
k
,
,
d
4
c
k
,
,
g
3
−g
2
f
eab
f
ecd
g
αγ
g
βδ
−g
αδ
g
βγ
+ f
eac
f
edb
g
αδ
g
βγ
−g
αβ
g
γδ
+ f
ead
f
ebc
g
αβ
g
γδ
−g
αγ
g
βδ
(2π)
4
δ
4
(k
1
+k
2
+k
3
+k
4
), (20)
m ,,ak
cq
,
bp,
−igf
abc
p
µ
(2π)
4
δ
4
( p −k −q). (21)
EXAMPLE
4.3 Fadeev–Popov Ghost Fields
To define the gluon propagator (see (15) of the last Example) properly one has
to specify a gauge. Otherwise the equation of motion (Maxwell equation) of the
free gluon field cannot be inverted to give the Green function of the field equa-
tion. This problem is already familiar from Abelian theories as QED. If we write
the Lagrangian of the free photon field as
L =−
1
4
F
2
=−
1
2
∂
µ
A
ν
(∂
µ
A
ν
−∂
ν
A
µ
)
=
1
2
A
ν
g
µν
∂
2
−∂
µ
∂
ν
A
µ
, (1)

4.2 The Gauge Theory of Quark–Quark Interactions 179
where a surface term is discarded after partial integration, the photon propaga-
tor D
µν
is the inverse of the sandwiched operator in (1)
g
µν
∂
2
−∂
µ
∂
ν
D
νλ
(x −y) =δ
µ
λ
δ(x −y). (2)
If we multiply (2) by the operator ∂
µ
,giving
(0 ·∂
ν
)D
νλ
(x −y) = ∂
λ
δ(x −y), (3)
we see that D
µν
is infinite. This is because the operator
g
µν
∂
2
−∂
µ
∂
ν
has no
inverse. This is the projection operator onto tranverse modes. It is a general fea-
ture of projection operators that they do not have an inverse, e.g. applied to an
arbitrary function ∂
µ
Λ it gives
g
µν
∂
2
−∂
µ
∂
ν
∂
µ
Λ = (∂
ν
∂
2
−∂
2
∂
ν
)Λ = 0 . (4)
Indeed the operator has a zero eigenvalue and therefore cannot be inverted. The
physical reason behind this is that one has to make sure to propagate only physi-
cal degrees of freedom. All fields that are related only by gauge transformations
A
µ
→ A
µ
+∂
µ
Λ are propagated as well, which clearly gives an infinite contri-
bution. This can be cured by fixing a particular gauge. To be definite we impose
the Lorentz condition
∂
µ
A
µ
=0 , (5)
which can be included in the Lagrangian in the general form
L
fix
=−
1
2λ
(∂
µ
A
µ
)
2
=
1
2λ
A
µ
g
µν
∂
2
A
ν
, (6)
where λ is some arbitrary gauge parameter. Again a surface term has been
neglected. If we include the gauge fixing in (1), the arising operator is well
defined,
1
2
A
µ
g
µν
∂
2
−(1 −λ
−1
)∂
µ
∂
ν
A
ν
, (7)
and can be inverted to give the photon propagator in momentum space,
D
µν
(k) =−
1
k
2
g
µν
−(1 −λ)
k
µ
kν
k
2
, (8)
where λ → 1 corresponds to the Feynman and λ → 0 to the Landau gauge. How-
ever, in QED such a gauge-fixing term does not affect the general physics of
the theory because the field χ = ∂
µ
A
µ
, i.e. the longitudinal part of the pho-
ton field does not interact with physical degrees of freedom. According to the
Abelian Maxwell equation it obeys a free field equation ∂
2
χ = 0 and therefore
Example 4.3

180 4. Gauge Theories and Quantum-Chromodynamics
Example 4.3
does not mix with the transverse part of the photon field. The corresponding situ-
ation for non-Abelian theories is much more complicated. For instance in QCD
the gauge-fixing field χ
a
=∂
µ
A
a
µ
obeys the non-Abelian extension of the wave
equation
∂
2
χ
a
+gf
abc
A
b µ
∂
µ
χ
c
= 0 . (9)
Therefore the unphysical χ particles, i.e. the longitudinal part of the gluon field,
can interact with the transverse (physical) components of A
a
µ
. Those unphysical
longitudinal components contribute to gluon loops and therefore have to be sub-
stracted. This substraction can be done by the introduction of unphysical ghost
fields η
a
that exactly cancel the χ
a
fields. The introduction of the η
a
fields is
most conviently done in the framework of path integral quantization
6
and was
first done by De Witt, Fadeev, and Popov. In this framework it can be shown that
the so-called Fadeev–Popov ghost fields obey the same equation (9) as the scalar
χ
a
fields, although they have to be quantized as fermion fields. Then, according
to Fermi–Dirac statistics, each closed loop of ghost fields has to be accompanied
by a factor −1. For each gluon loop one has to include one ghost loop which can-
cels exactly the longitudinal part of the gluons. The complete gauge-fixing term
then can be written as
L = L
fix
+L
F.P.
(10)
with
L
F.P.
=∂
µ
η
a †
∂
µ
η
a
+gf
abc
A
b,µ
η
c
=−η
a †
∂
µ
D
ac
µ
η
c
, (11)
where again a surface term is neglected. From this Lagrangian one can derive the
Feynman rules for the ghost propagators and ghost vertices.
EXAMPLE
4.4 The Running Coupling Constant
We discussed above that in general a perturbation series converges for a given
coupling constant only at some momentum transfers. This behavior is easily
understood, since the renormalized coupling constant is defined for a specific
momentum transfer. In QED, for example, one can choose the incoming and
outgoing photons to be on the mass shell, and then
ee
q
m
q
m
6
See, e.g., W. Greiner and J. Reinhard: Field Quantization (Springer, Berlin, Heidel-
berg, 1996).
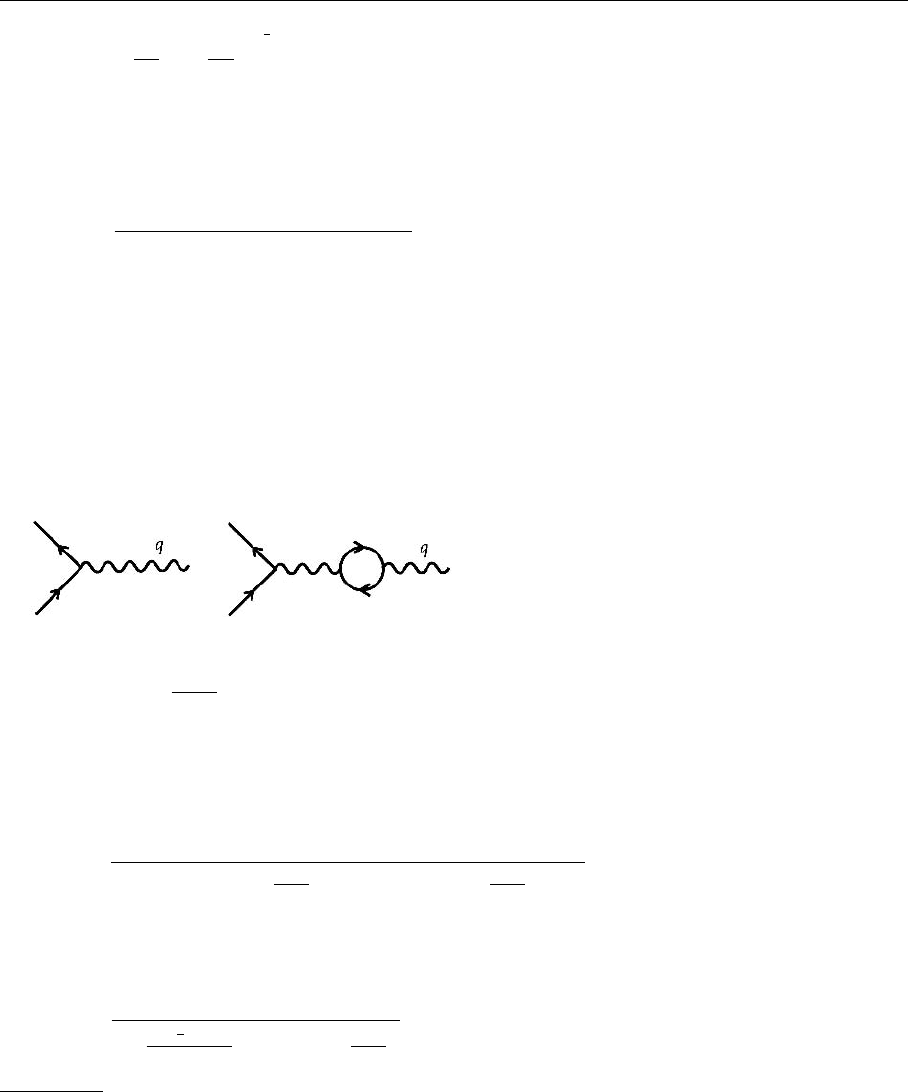
4.2 The Gauge Theory of Quark–Quark Interactions 181
e
R
= e
1 −
α
2π
log
Λ
2
m
2
1
2
for q
2
=0 . (1)
For other values of q
2
this graph then yields a finite, q
2
-dependent renormaliza-
tion, i.e., a finite additional contribution to every electromagnetic process. These
corrections can be given analytically and taken into account by a redefinition of
the electric charge. We obtain in a massless QED
7
e
2
R
q
2
=
e
2
R
q
2
=−M
2
1 −Ce
2
R
q
2
=−M
2
ln
q
2
/ −M
2
. (2)
The value of the constant C depends on the number of fermions considered
by the theory and on the fermion charges. From (2) it also follows that q
2
= 0
is a special value, quite unsuitable for renormalization (here e
R
is equal to
zero). Therefore q
2
=−M
2
is usually chosen as the renormalization point.
Equation (2) denotes the additional contributions to all massless QED graphs
caused by vacuum polarization. e
2
R
(q
2
) is valid only for a certain q
2
range: if
q
2
< 0, Ce
2
R
−M
2
ln
q
2
/ −M
2
< 1. In this range it can be interpreted as
a physical charge. For q
2
> 0, e
2
R
(q
2
) becomes formally complex and such an
interpretation is no longer possible. In the latter case e
2
R
(q
2
) reflects the fact that
the following graphs lead to different phases.
(3)
The divergence of this “charge” for
Ce
2
R
−M
2
ln
q
2
−M
2
→1
indicates the breakdown of perturbation theory. For values of −q
2
this large
the contributions of two-loop corrections become as large as those of one-loop
graphs in (1), and so on. If the higher corrections are also taken into account, we
obtain instead of (2) the nonconvergent expression
e
2
(q
2
) =
e
2
(−M
2
)
1 −Ce
2
(−M
2
) ln
q
2
−M
2
+C
e
4
(−M
2
) ln
2
q
2
−M
2
+...
. (4)
Since QCD is a scale-free theory, it is possible to define a running coupling con-
stant for it, which takes the finite corrections due to the graphs shown in Fig. 4.7
into account. We get
α
s
(q
2
) =
α
s
(−M
2
)
1 +
11−
2
3
N
f
(q
2
)
4π
α
s
(−M
2
) ln
q
2
−M
2
, (5)
7
see W. Greiner and J. Reinhardt: Quantum Electrodynamics, 3rd ed. (Springer, Berlin,
Heidelberg, 2003).
Example 4.4
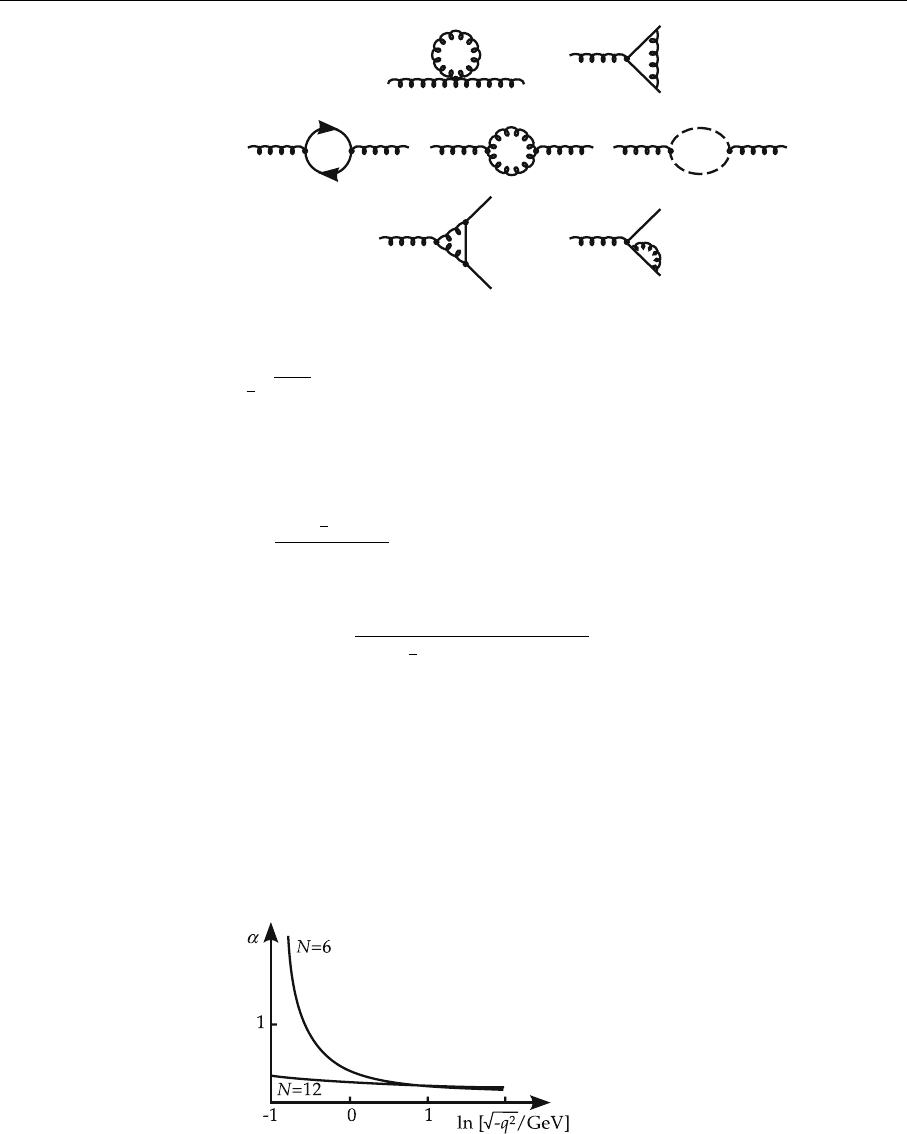
182 4. Gauge Theories and Quantum-Chromodynamics
q
q
qq
qq
Fig. 4.7. QCD graphs taken
into account by α
s
(q
2
)
Fig. 4.8. Running coupling
constants for the unphysi-
cal case of 6 and 12 dif-
ferent massless quarks. Both
curves assume
α(−100 GeV
2
) =0.2
where N
f
denotes the number of quark flavors with a mass much smaller than
1
2
"
−q
2
. We shall derive (5) in Sect. 4.4 after having introduced the necessary
techniques in Sect. 4.3. Here we only want to discuss its phenomenological
meaning. Equation (5) includes two parameters M
2
and α
s
(M
2
),which,how-
ever, are not independent of each other. It is possible to introduce a quantity
Λ = Λ(M) such that
11 −
2
3
N
f
(q
2
)
4π
α
s
(−M
2
) ln(Λ
2
/M
2
) =−1 , (6)
leading to
α
s
(q
2
) =
4π
(11 −
2
3
N
f
(q
2
))ln(−q
2
/Λ
2
)
. (7)
Hence the running coupling constant is fixed for all momentum transfers by
one parameter. Λ can be determined by investigating highly energetic e
+
e
−
pair
annihilation and many other processes. The “world average” of these results is
α
s
−(34 GeV)
2
≈0.14 ±0.02 . (8)
Clearly the q
2
dependence of the strong coupling constant is determined by N
f
,
i.e., the number of quarks with M
2
< |q
2
|. In Fig. 4.8, (7) is plotted for N
f
=6
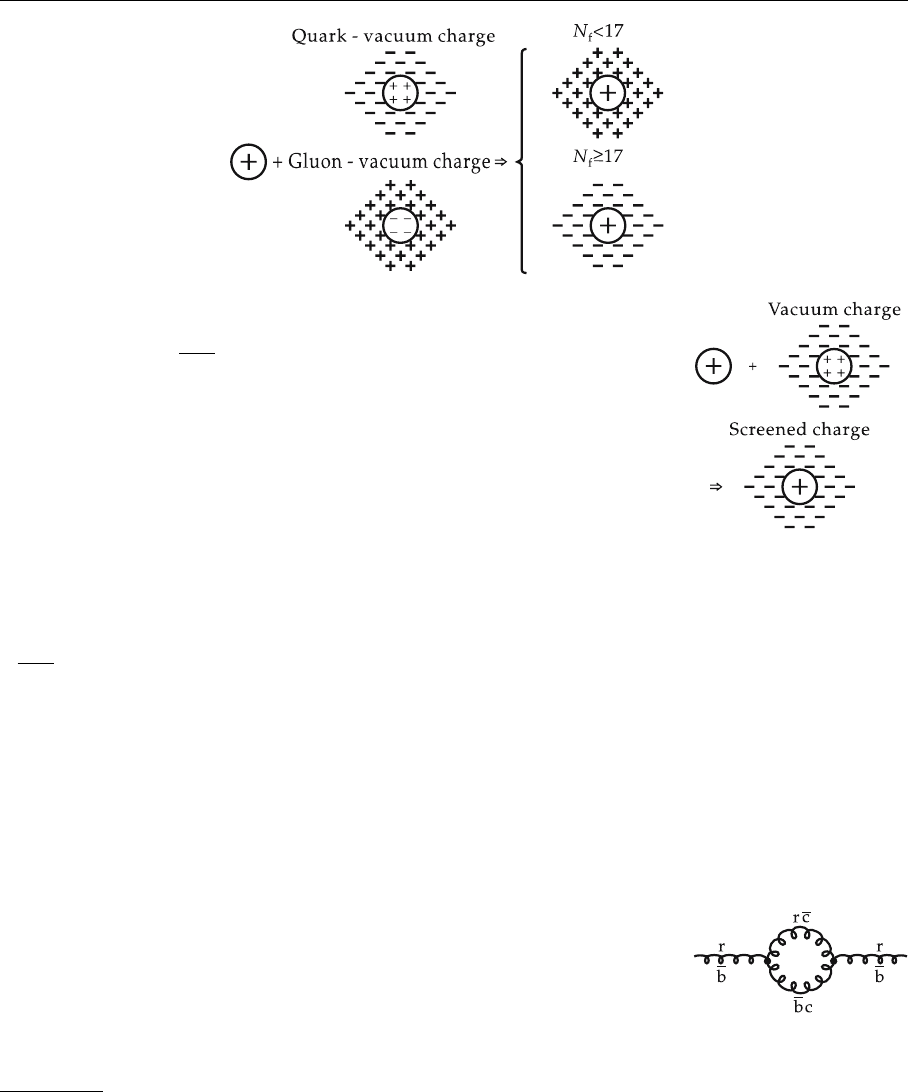
4.2 The Gauge Theory of Quark–Quark Interactions 183
Fig. 4.9. Charge screening
in QCD. N
f
denotes the
number of (massless) quarks
and N
f
= 12. Λ has been fixed to obey (8). The plot for N
f
=6 increases rapidly
for small values of
"
−q
2
, i.e., the interaction can certainly not be described by
perturbation theory below 500 MeV energy transfer. This conclusion is not valid
for N
f
=12. Since at these energies the real physical hadrons have a strongly
correlated structure rather than appearing as a group of free quarks, it follows im-
mediately that the number of “light” quarks cannot be much greater than six. In
fact only two “light”-quark doublets have been discovered. This example yields
α
s
−(100 GeV)
2
=0.2 ⇒ Λ = 112 MeV for N
f
=6 . (9)
The currently discussed values for the scale parameter of QCD, Λ
QCD
, range
from 100 MeV to 300 MeV. It should be mentioned that Fig. 4.8 contains an in-
valid simplification. In contradiction to this figure, N
f
decreases with decreasing
"
−q
2
, because an increasing number of quarks must be considered massive.
Equation (7) can be interpreted as antiscreening of the charge unlike the usual
screening in QED. The vacuum polarization graph in (1) leads in the case of QED
to a polarization of the vacuum, which in the context of field theory is a medium
with well-defined, non-trivial features.
8
This behavior is depicted in Fig. 4.10
for an extended charge. In QCD the corresponding graph with a virtual quark
loop shows the same effect. Here, however, there is also a gluon contribution.
Since the gluons carry a charge, their virtual excitations can also be polarized.
Therefore the analogous graph in Fig. 4.9 is somewhat more complicated. In
particular, the total charge distribution depends on the dominance of the quark
or gluon part. Although the latter is defined by the gauge group, the first part
increases with every additional quark until it dominates the theory and QCD
shows the same behavior as QED. From this argument it also follows that the
antiscreening in SU(N) gauge theories in principle increases with N.Eventhe
explicit form of that dependence can be understood. The gluon contribution is
simply proportional to the number of possible permutations for the loop gluons
in Fig. 4.11.
8
see W. Greiner and J. Reinhardt: Quantum Electrodynamics, 3rd ed. (Springer, Berlin,
Heidelberg, 2003)
Fig. 4.10. Charge screening
in QED
Fig. 4.11. Gluon vacuum
polarization for QCD
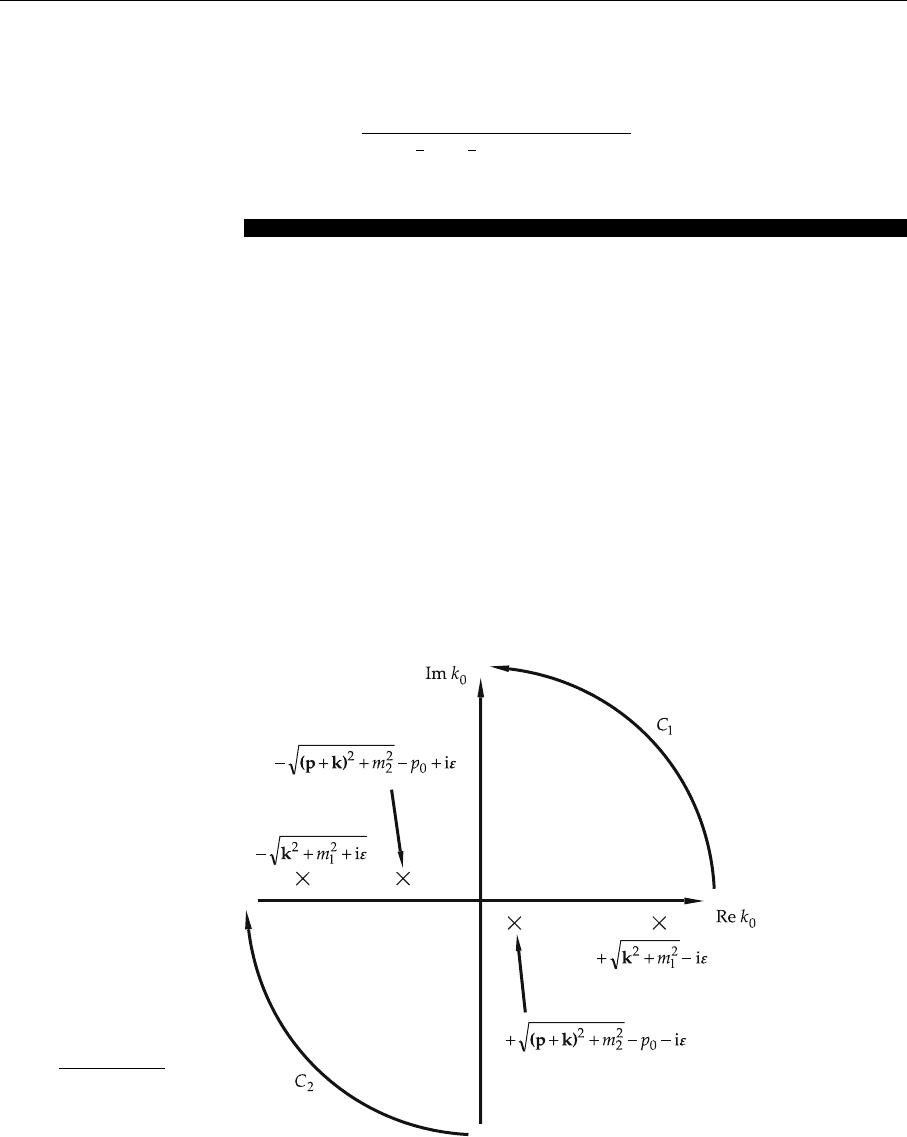
184 4. Gauge Theories and Quantum-Chromodynamics
Example 4.4
Fig. 4.12. Poles of the
integrand in (4.59) for
p
0
<
( p +k)
2
+m
2
2
.Inte-
gration contours C
1
and C
2
are those used in (4.60)
ForQCD,i.e.SU(3),c can assume three values; for SU(N) there are cor-
respondingly N values. Therefore (7) becomes, in the case of an SU(N)gauge
theory,
α
N
(q
2
) =
4π
11 ×
1
3
N −
2
3
N
f
ln
−q
2
/Λ
2
N
. (10)
4.3 Dimensional Regularization
Currently so-called dimensional regularization is considered to be the standard
procedure for regularizing quantum field theories. Only in special cases, where
some specific disadvantages of this method show up, are other procedures, such
as Pauli–Villars regularization or the momentum-cutoff method, employed. For
lattice gauge theories, however, regularization is automatically provided by the
lattice constant, which necessarily yields a rather special regularization scheme.
In the following we discuss only dimensional regularization.
The basic observation that motivated dimensional regularization is that only
logarithmic divergences in standard quantum field theories are encountered and
4.3 Dimensional Regularization 185
these vanish for any dimensionality smaller than 4. Thus if it is possible to define
a generalized integration for noninteger dimensions “d” the usual divergences
will show up as poles in “d −4” which should be relatively easy to isolate. To
realize this idea it is advisable first to simplify the divergences that occur by
a trick known as “Wick rotation”, namely by continuing it to imaginary energies.
As mentioned above, only logarithmic divergences are encountered, so a typical
divergent integral has the form
i
d
4
k
1
(k
2
−m
2
1
+iε)
1
( p +k)
2
−m
2
2
+iε
. (4.59)
One awkward property of this integral is that its behavior for large k
µ
is not uni-
form, since k
2
=(k
0
)
2
−(k)
2
can stay small even when k
0
and |k| both become
large. This problem can be circumvented by continuing k
0
to ik
0
E
(k →k
E
),
implying that
k
2
→−(k
0
E
)
2
−(k
E
)
2
=−k
2
E
,
with k
2
E
=(k
0
E
)
2
+(k
E
)
2
. (k
E
)
µ
is obviously a Cartesian vector that becomes
uniformly large if (k
E
)
µ
→∞, so it is much easier to analyze the ultraviolet
divergences for (k
E
)
µ
than for k
µ
.
To perform the Wick rotation one has to deform the integration path of k
0
in
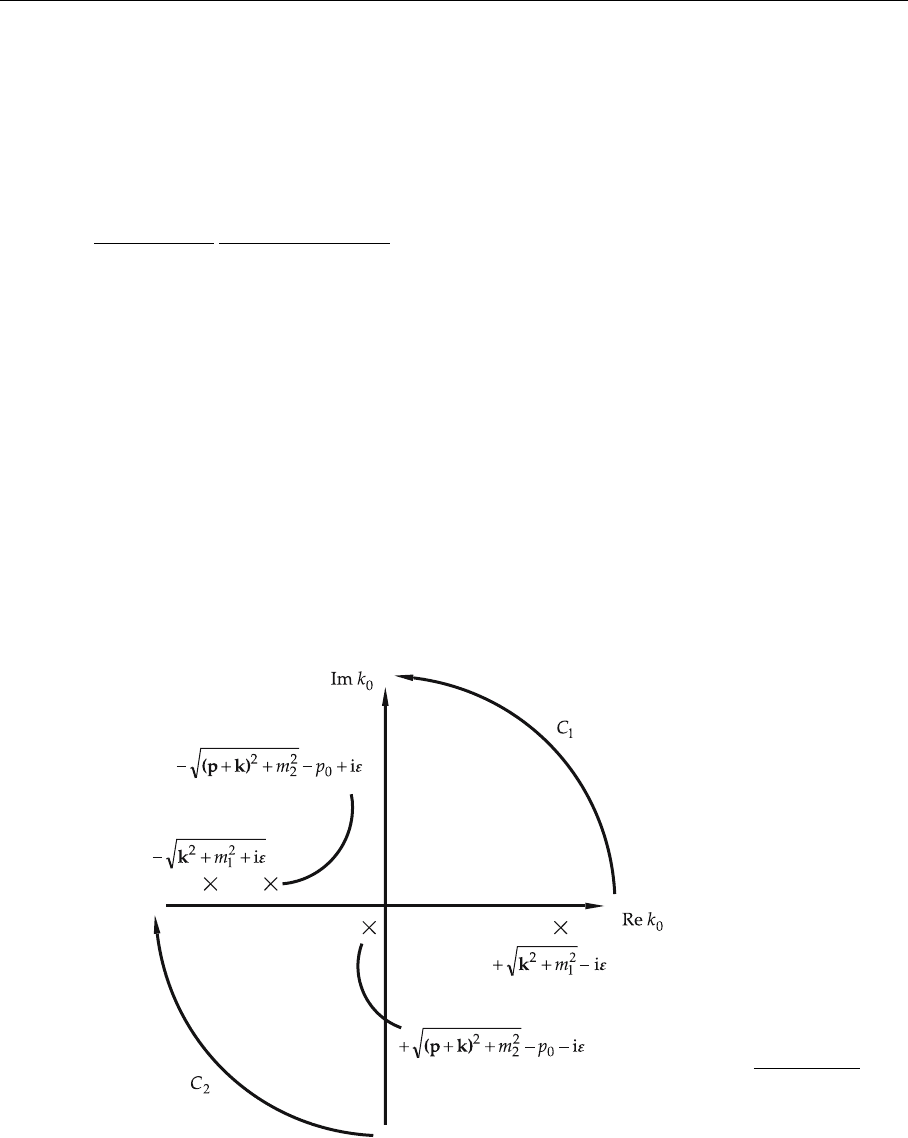
the complex plane. Figures 4.12 and 4.13 show the positions of the poles. We
Fig. 4.13. Poles of the
integrand in (4.59) for
p
0
>
( p +k)
2
+m
2
2
.Inte-
gration contours C
1
and C
2
are those used in (4.60)

186 4. Gauge Theories and Quantum-Chromodynamics
now use
∞
−∞
dk
0
···+
−i∞
+i∞
dk
0
···+
C
1
dk
0
···+
C
2
dk
0
...
=
⎧
⎨
⎩
0 for Fig. 4.12
residue for k
0
=
( p +k)
2
+m
2
2
− p
0
; for Fig. 4.13
. (4.60)
The ε prescription in (4.59) guarantees that the integrals over the arcs at infinity,
+
C
1
dk
0
and
+
C
2
dk
0
, vanish. This can easily be seen if we use
1
(k
2
−m
2
1
+iε)
1
( p +k)
2
−m
2
2
+iε
=−i
∞
0
dα e
iα(k
2
−m
2
1
+iε)
(−i)
∞
0
dβ e
iβ
( p+k)
2
−m
2
2
+iε
. (4.61)
From k
0
= R e
iϕ
,0≤ϕ ≤
π
2
,andπ ≤ ϕ ≤
3
2
π with R →∞,weget
Im(k
2
) = R
2
sin(2ϕ) +O(R)>0 , (4.62)
such that all terms vanish exponentially. The result of the Wick rotation is
therefore
i
∞
−∞
d
4
k
1
k
2
−m
2
1
+iε
1
( p +k)
2
−m
2
2
+iε
=−
∞
−∞
d
4
k
E
1
k
2
E
+m
2
1
−iε
1
( p
E
+k
E
)
2
+m
2
2
−iε
+ possibly a finite residuum . (4.63)
The residuum that possibly appears is finite. As we intend to isolate and substract
the divergent part of the integral (4.59) we do not have to bother about this finite
contribution. We define the r enormalized integral as (4.59) minus the divergent
part of (4.63). This definition is not affected by the finite residuum.
Next we proceed to define an abstract mathematical operation which we want
to call the d-dimensional integral:
d
d
k
E
f(k
E
).

4.3 Dimensional Regularization 187
First we impose the following conditions:
(1) Linearity
d
d
k
E
[af(k
Eµ
) +bg(k
Eµ
)]
=a
d
d
k
E
f(k
Eµ
) +b
d
d
k
E
g(k
Eµ
). (4.64)
(2) Invariance of the integral under finite shifts (p
µ
finite)
d
d
k
E
f(k
Eµ
) =
d
d
k
E
f(k
Eµ
+ p
Eµ
). (4.65)
(3) A scaling property
d
d
k
E
f(λk
Eµ
) = λ
−d
d
d
k
E
f(k
Eµ
). (4.66)
From these definitions it is not clear what is meant by a Lorentz-vector k
µ
in
d dimensions. The point is that it is always sufficient to treat scalar integrals.
Any vectorlike integral is completely specified by its values if contracted with
few linearly independent vectors and those scalar integrals can be analytically
continued. Bearing this in mind it is, however, helpful to use vectors like k
µ
as
a shorthand for a collection of suitably defined scalar products.
The d-dimensional integral is now defined by its action on a set of basis
functions
λ(A, P
µ
) = e
−A(k+P)
2
. (4.67)
Properties (4.64) and (4.65) guarantee that all functions decomposed in this basis
can be integrated once the integral
d
d
k
E
e
−Ak
2
E
(4.68)
is known. Here the scaling property (4.66) becomes important, since it reduces
any such integral to a single one:
d
d
k
E
e
−Ak
2
E
= A
−
d
2
d
d
k
E
e
−k
2
E
. (4.69)
As we want the d -dimensional integral to coincide with the usual one for integer
values of d we impose the condition
d
d
k
E
e
−k
2
E
=π
d
2
. (4.70)
