Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


158 4. Gauge Theories and Quantum-Chromodynamics
EXAMPLE
4.1 The Geometric Formulation of Gauge Symmetries
For the sake of simplicity we consider a specific example, namely a set of spinor
fields Ψ
i
(x), i = 1, 2,..., N, combined as a vector
Ψ =
⎛
⎜
⎜
⎝
Ψ
1
(x)
Ψ
2
(x)
.
.
.
Ψ
N
(x)
⎞
⎟
⎟
⎠
. (1)
Furthermore we assume a local symmetry such that
Ψ
(x) = exp
+ig
ˆ
θ(x)
Ψ(x) (2)
is equivalent to Ψ(x). This situation is analogous to an arbitrary, e.g., contravari-
ant, vector and its Lorentz transform:
V
µ
(x), V
µ
(x) = Λ
µ
ν
(x)V
ν
(x). (3)
The Lorentz transformation Λ(x) corresponds in this case to the gauge trans-
formation exp
−ig
ˆ
θ(x)
. A well-known technical problem in the theory of rel-
ativity is the definition of a vector (in general a tensor) derivative. The evaluation
of a quotient of differences
V
µ
(x +h) −V
µ
(x)
h
(4)
yields additional terms owing to the dependence of the metric tensor g
µν
(x) on
the position vector x.
This problem leads to the definition of the covariant derivative
V
µ
ν
:=∂
ν
V
µ
+Γ
µ
αν
V
α
(5)
with so-called Christoffel symbols Γ
µ
αν
,
Γ
µ
αν
=−
1
2
g
µσ
(∂
ν
g
ασ
+∂
α
g
σν
−∂
σ
g
να
), (6)
representing the position dependence of the metric, that is, the local coordinate
systems. The covariant derivative (5) constructed in this way is invariant under
Lorentz transformations.
In a completely analogous manner we can write (5) for the spinor fields Ψ :
∂
µ
Ψ(x) →
∂
µ
+
ˆ
Γ
µ
(x)
Ψ(x) =: D
µ
Ψ(x), (7)
where
ˆ
Γ
µ
(x) is a position-dependent matrix with respect to the vectors Ψ .
ˆ
Γ
µ
(x)
is determined by the requirement that the covariant derivative D
µ
Ψ(x) has to

4.1 The Standard Model: A Typical Gauge Theory 159
be invariant under gauge transformations exp
−ig
ˆ
θ
that correspond to the
Lorentz transformations. Writing −ig
ˆ
A
µ
instead of
ˆ
Γ
µ
we have
iD
µ
Ψ(x) =
ˆ
p
µ
+g
ˆ
A
µ
Ψ(x), (8)
Ψ(x) →Ψ
(x) = e
ig
ˆ
θ(x)
Ψ(x), (9)
ˆ
A
µ
→
ˆ
A
µ
= e
ig
ˆ
θ(x)
ˆ
A
µ
(x) −
i
g
∂
µ
e
−ig
ˆ
θ(x)
. (10)
Interpreted geometrically, (5) is an effect of parallel transport. To evaluate (4),
the vector V
µ
has to be transported from the position x +h to the point x.Butin
a position-dependent coordinate system this transport changes the vector’s coor-
dinate representation (think, for example, of the coordinates r, θ,andϕ of a fixed
vector which moves on the surface of a sphere). Γ
µ
αν
V
α
describes this change,
which has to be added to ∂
ν
V
µ
in order to reveal the physical, coordinate-
independent change of the vector V
µ
. Correspondingly,
ˆ
A
µ
−
ˆ
A
µ
represents the
change of Ψ due to the position dependence of the gauge (see Fig. 4.1). Since
the covariant derivatives are gauge independent and invariant under Lorentz
transformations, this is also valid for their commutator:
ˆ
D
µ
,
ˆ
D
ν
=
∂
µ
−ig
ˆ
A
µ
,
∂
ν
−ig
ˆ
A
ν
=−ig∂
µ
ˆ
A
ν
+ig∂
ν
ˆ
A
µ
−g
2
ˆ
A
µ
,
ˆ
A
ν
=−ig
∂
µ
ˆ
A
ν
−∂
ν
ˆ
A
µ
−ig
ˆ
A
µ
,
ˆ
A
ν
=−ig
ˆ
F
µν
. (11)
The
ˆ
F
µν
represent the physical part of the gauge fields, i.e., the part that cannot
be changed by simply choosing another gauge. Correspondingly, in the theory
of relativity we obtain the curvature tensor R
µ
νσ
, describing the physical part
of space curvature, i.e., the part that is not due only to the chosen coordinate sys-
tem. Also R
µ
νσ
is simply the commutator of the covariant derivatives (5), with
additional terms occurring for the covariant indices. For example, for a tensor it
holds that
T
β
α;τ
= T
β
α,τ
+Γ
β
µτ
T
µ
α
−Γ
µ
ατ
T
β
µ
. (12)
Fig. 4.1. The interpretation
of
ˆ
A as a description of par-
allel transport
Example 4.1
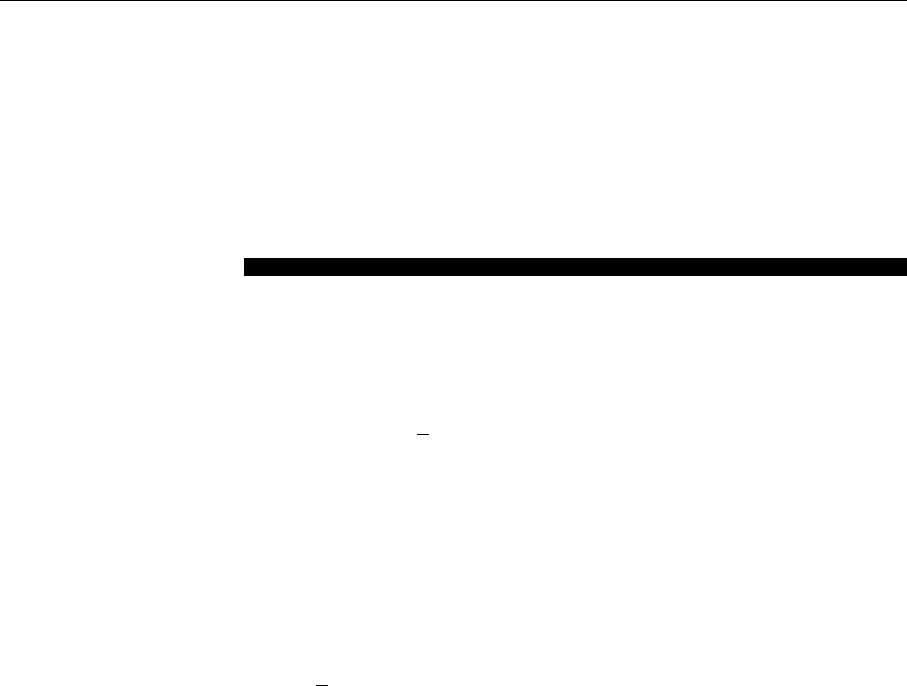
160 4. Gauge Theories and Quantum-Chromodynamics
Example 4.1
Because of the outlined similarity one could also focus on gauge symmetries
and interpret the general theory of relativity as a special gauge theory. This kind
of consideration would shift the whole discussion to the formal definition of
a gauge group. Terms like parallel transport or curvature would not play any role.
Covariant derivatives and field tensors
ˆ
F
µν
would be defined by their invariance
properties. Only at the very end of such a treatment would one try to connect the
obtained structures with physics. Consequently one is free to choose between un-
derstanding general relativity as a gauge theory and interpreting gauge theories
geometrically.
To formulate the standard model we need an additional concept, namely the idea
of spontaneous symmetry breaking. Again the basic idea can be explained quite
easily. If scalar fields are considered, interaction terms of the form φ
4
and φ
2
can
be renormalized. Therefore the Lagrangian
L =−Φ
+
Φ −
λ
4
Φ
+
Φ −v
2
2
(4.9)
sets up a well-defined field theory. (Such scalar quantum field theories are in fact
somewhat problematic. It is possible that consistent renormalization requires the
coupling constant to be zero. This possibility is called “triviality” and implies
that (4.9) makes sense only if the scalar Higgs particle, for example, has some
internal structure on the 1–10 TeV scale. For its phenomenological properties at
the energies we consider this is irrelevant.) Within the meaning of the Lagrange
formalism the second term has to be interpreted as a contribution to the potential
energy:
V =
λ
4
Φ
+
Φ −v
2
2
. (4.10)
Clearly the energy is minimal for |φ|=v = const. Hence this is the physical
ground state. On the other hand, a problem occurs if the theory is quantized in
the standard way by means of commutator relations between field operators.
Since 0|
ˆ
φ|0≡0, the state with v =|φ|=vac|
ˆ
φ|vac cannot in principle be
constructed with one-particle excitations on the usual ground state. Therefore
the physical vacuum state |vac is not identical with the field theoretical vac-
uum state, |vac=|0. The physical excitations are only obtained if fluctuations
around φ = v are considered and if
ˆ
φ(x) is quantized in the usual manner:
Φ(x) →v +
ˆ
Φ(x), vac|
ˆ
Φ|vac=0 . (4.11)
There is no deeper physical reason for the fact that the excitations around φ = 0
and φ = v cannot be expressed by each other. It only means that the canoni-
cal quantization scheme is not complete. In fact it is possible to choose another
quantization method without this disadvantage, e.g. quantization with functional
integrals. We cite here without proof the following essential statement:
If a (gauge) theory is renormalizable for Φ(x) = v +λ(
x), i.e., for quanti-
zation ar ound Φ(x) = v, then it is also renormalizable for quantization around
Φ(x) =0 and vice versa.

4.1 The Standard Model: A Typical Gauge Theory 161
This makes the following trick possible. All particle masses M
i
are replaced
by
M
i
→
Φ(x)
v
M
i
. (4.12)
For physical states one has to set φ(x) = v +χ(x). This yields just M
i
plus an ad-
ditional interaction term, whose meaning will be explained later. So long as this
term does not cause significant physical effects, the original theory has practi-
cally not been changed. In this case the theory is then exactly renormalizable if
it is also renormalizable for a quantization around φ(x) =0, i.e., for vanishing
mass terms. As it is possible to prove that certain classes of massless gauge the-
ories are renormalizable, this is also true for the resulting theories with masses
generated by (4.12), i.e., by spontaneous symmetry breaking. The crucial point
is that spontaneous symmetry breaking preserves gauge invariance, which is
essential for the proof of renormalizability.
In general, φ(x) is not a scalar with respect to the current gauge symmetry
(i.e. not a singlet) but rather a multiplet. The vacuum expectation value v then
defines a particular direction within this multiplet. Because of this, one speaks
of spontaneous symmetry breaking. This expression is quite misleading since
the symmetry is really preserved. The choice of v should instead be compared
with the choice of a specific direction of quantization in a spherically symmet-
ric problem. Now we want to discuss spontaneous symmetry breaking for the
special case of the standard model.
The standard model describes the electromagnetic and weak interactions.
The latter was first understood as a four-fermion interaction between, for ex-
ample, a neutron, proton, electron, and antineutrino. But it has been clear for
a long time that this can be an effective description only for a microscopic pro-
cess, e.g., the exchange of charged so-called W bosons (see Fig. 4.2). Since the
W fields are vectors and mediate an interaction (just like the photon), it is natural
to regard them as gauge fields of a gauge group. Choosing possible candidates
for this gauge group does not cause any difficulties, if the following points are
considered:
(1) The leptons exclusively couple to the corresponding neutrinos, for ex-
ample the electron only to the electron neutrino. Therefore we have to choose
a group with an irreducible two-dimensional representation if we want to avoid
additional artificial assumptions.
Fig. 4.2. The Fermi interac-
tion and its interpretation as
the exchange of charged W
bosons

162 4. Gauge Theories and Quantum-Chromodynamics
(2) Except for W
+
and W
−
only a minimum number of additional gauge fields
should be postulated. Hence the number of generators should be slightly bigger
than two.
These requirements lead directly to the group SU(2). But the SU(2) contains
three generators. One could therefore try to identify the additional third gauge
field with the photon. However, it is not possible to carry out this idea consis-
tently. The construction principles which have been outlined so far and which
will be applied in the following example demand a new neutral particle, the Z
0
,
to be postulated. This involves the existence of a new interaction: so-called neu-
tral currents. The experimental verification of this interaction and of the W and
Z particles is one of the greatest triumphs of particle physics.
Hence SU(2) × U(1) is the gauge group of the GSW model. The most
frequently used representation of the matrices λ
i
is
λ
1
=
01
10
,λ
2
=
0 −i
i0
,λ
3
=
10
0 −1
,λ
4
=
10
01
,
(4.13)
i.e., nothing more than the Pauli matrices for SU(2) and the unit matrix for
U(1) (remember that the generators act on the doublet states). If we denote the
corresponding gauge fields by W
µ
1
, W
µ
2
, W
µ
3
,andB
µ
,then
ˆ
F
µν
from (4.6) is
(i, j, k = 1, 2, 3)
ˆ
F
µν
= ∂
µ
λ
j
2
W
j
ν
+
11
2
·B
ν
−∂
ν
λ
j
2
W
j
µ
+
11
2
·B
µ
+gε
ijk
λ
k
W
i
µ
W
j
ν
,
(4.14)
since
11 commutes with all matrices. Because
tr{λ
i
λ
j
}=2δ
ij
, tr{λ
i
}=0 , (4.15)
L
0
is divided into two contributions, where we replace W
i
µ
and B
µ
by
1
2
W
j
µ
and
1
2
B
µ
, respectively, in order to obtain the usual factor (usually t
i
=
1
2
λ
i
rather
than λ
i
are chosen for the matrices):
L
0
=−
1
4
W
j
µν
W
jµν
−
1
4
B
µν
B
µν
, (4.16)
W
j
µν
=∂
µ
W
j
ν
−∂
ν
W
j
µ
−gε
ijk
W
i
µ
W
k
ν
, (4.17)
B
µν
=∂
µ
B
ν
−∂
ν
B
µ
. (4.18)
Also (4.7) can be written down directly for the gauge group SU(2) × U(1). The
only real novelty is the appearance of two coupling constants g and g
for the two
gauge groups SU(2) and U(1):
L
int
=Ψ
p
µ
+gW
j
µ
λ
j
2
+g
B
µ
γ
µ
Ψ. (4.19)
Clearly the total Lagrangian L
0
+L
int
is then invariant under the transformations
λ
j
2
W
j
µ
→exp
igθ
j
λ
j
2
λ
j
2
W
j
µ
+
i
g
∂
µ
exp
−igθ
j
λ
j
2
, (4.20)

4.1 The Standard Model: A Typical Gauge Theory 163
11
2
B
µ
→exp
ig
11
2
θ
(x)
11
2
B
µ
+
i
g
∂
µ
exp
−ig
11
2
θ
(x)
= B
µ
+∂
µ
θ
(x), (4.21)
Ψ(x) →exp
igθ
j
(x)
λ
j
2
exp
ig
11
2
θ
(x)
Ψ(x). (4.22)
Since the U(1) transformations commute, (4.21) has a very simple form (just
as in electrodynamics). Because of this simple feature one can allow different
fermions to transform differently under U(1). If we replace (4.19) and (4.22) by
L
int
=
j
Ψ
f
p
µ
+gW
j
µ
λ
j
2
+g
y
f
2
B
µ
γ
µ
Ψ
f
, (4.23)
Ψ(x) →exp
igθ
j
(x)
λ
j
2
exp
ig
y
f
2
θ
(x)
Ψ
f
(4.24)
with arbitrary numbers y
f
, then the SU(2) ×U(1) symmetry still remains valid.
As mentioned earlier, the spinor doublet is identified with, for example,
the electron and the electron–neutrino field; usually ν
e
is written as the upper
component:
Ψ
f
=
ν
e
e
L
. (4.25)
Here we also took the experimenal observation into account that only left-handed
leptons and quarks interact weakly:
e
L
=
1 −γ
5
2
e . (4.26)
Equation (4.25) then yields the structure of the remaining fermion doublets:
Ψ
f
:
ν
µ
µ
L
,
ν
τ
τ
L
,
u
d
L
,
c
s
L
,
t
b
L
, ··· . (4.27)
Here the quark fields d
,s
,andb
are orthogonal superpositions of the mass
eigenstates d, s, and b. The fact that the mass eigenstates differ from the eigen-
states with respect to the weak interaction is one of the most fascinating features
of the weak interaction. It is related to exotic effects such as kaon oscillations
and could be responsible for CP violation.
3
Lastly we still have to define the Higgs sector. For Higgs particles we choose
also the lowest SU(2) representation, namely the doublet:
φ =
φ
1
+iφ
2
φ
3
+iφ
4
,φ
1
,φ
2
,φ
3
, and φ
4
are real. (4.28)
3
See W. Greiner and B. Müller: Gauge Theory of Weak Interactions, 3rd ed. (Springer,
Berlin, Heidelberg 2000).
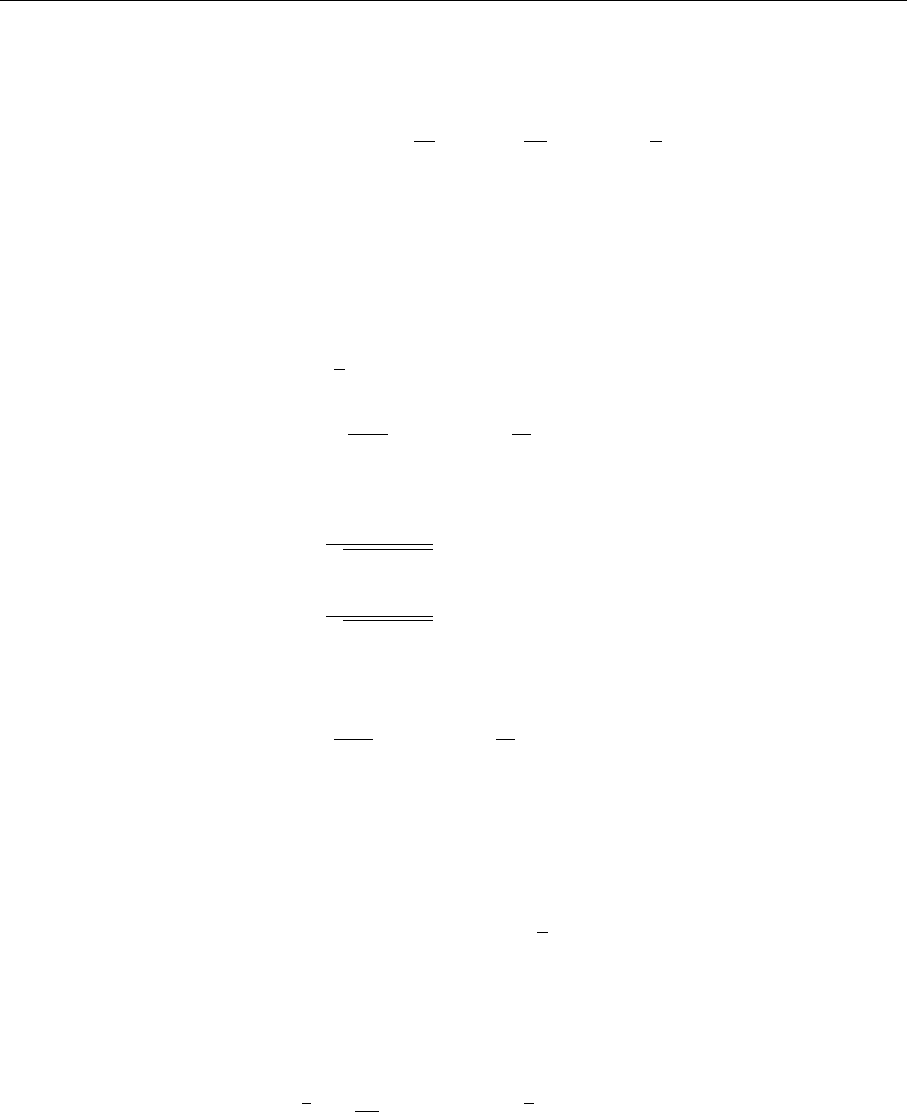
164 4. Gauge Theories and Quantum-Chromodynamics
To maintain the gauge invariance of the theory, for the φ field also all derivatives
have to be replaced by covariant derivatives (see Example 4.1). This yields the
Higgs Lagrangian
L
H
=
∂
µ
−ig
λ
j
2
W
j
µ
−ig
y
H
2
B
µ
φ
2
−
λ
4
φ
+
φ −v
2
2
. (4.29)
If now φ in L
H
is replaced by means of (4.11) by
φ →
0
v
+χ, (4.30)
for example, then (4.29) generates the gauge-field mass terms
L
H
→
1
4
g(W
1
µ
−iW
2
µ
)
g
y
H
B
µ
−gW
3
µ
2
v
2
=
g
2
v
2
4
W
2
1
+W
2
2
+
v
2
4
g
y
H
B
µ
−gW
3
µ
2
. (4.31)
Now we expand B
µ
and W
3
µ
into two new fields A
µ
and Z
µ
,
B
µ
=
1
g
2
+g
2
y
2
H
(g
y
H
Z
µ
−gA
µ
),
W
3
µ
=
1
g
2
+g
2
y
2
H
(−gZ
µ
−g
y
H
A
µ
), (4.32)
and obtain
L
H
→
g
2
v
2
4
(W
2
1
+W
2
2
) +
v
2
4
(g
2
+g
2
y
2
H
)Z
2
. (4.33)
The A
µ
field remains massless and is consequently identified with the photon.
One can also absorb y
H
in the definition of g
and with these identifications all
other y values follow. y, the so-called “weak hypercharge”,hastobechosenin
such a way that all particles get their correct electric charges, utilizing the well-
known Gell-Mann–Nishijima formula
y = 2(Q −t
3
) or Q =
y
2
+t
3
, (4.34)
where Q and t
3
denote the electric charge and the weak isospin of each particle,
respectively. Finally it is common practice also to generate the fermion masses
by spontaneous symmetry breaking. This can be achieved by replacing all mass
terms by corresponding couplings to the Higgs field:
m
e
ee →
m
e
v
ν
e
e
+
L
γ
0
φ e
R
+e
R
φ
+
ν
e
e
L
. (4.35)
4.2 The Gauge Theory of Quark–Quark Interactions 165
With these remarks we conclude our brief sketch of the standard model, which
has been experimentally verified to a remarkable degree. For an extensive discus-
sion we refer to Relativistic Quantum Mechanics
4
. At this point we turn to the
question of what an analogous theory for quark–quark interactions has to look
like.
4.2 The Gauge Theory of Quark–Quark Interactions
In order to construct a gauge theory of quark–quark interactions, one has first
of all to determine the number of “charge states”, i.e., the number of different
kinds of quarks with respect to the new interaction. Following our discussion in
Sect. 1.1 the minimum number of quarks needed is three. Now we want to give
several arguments indicating that there are exactly three quark states for every
quark flavor, i.e., three colors (N
c
=3).
The results of high-energy e
+
e
−
reactions provide the first argument. Here
hadrons are created by pair annihilation followed by the creation of quark-
antiquark pairs. We suppose that the interaction in the final channel which results
in hadronization does not influence the cross section. This assumption is con-
firmed by deep inelastic scattering experiments (see Chap. 3) and follows from
asymptotic freedom. The creation of quark-antiquark pairs can be compared to
the creation of, e. g., muon-antimuon pairs. In both cases, the cross section is
proportional to the square of the amplitude of the corresponding process. This
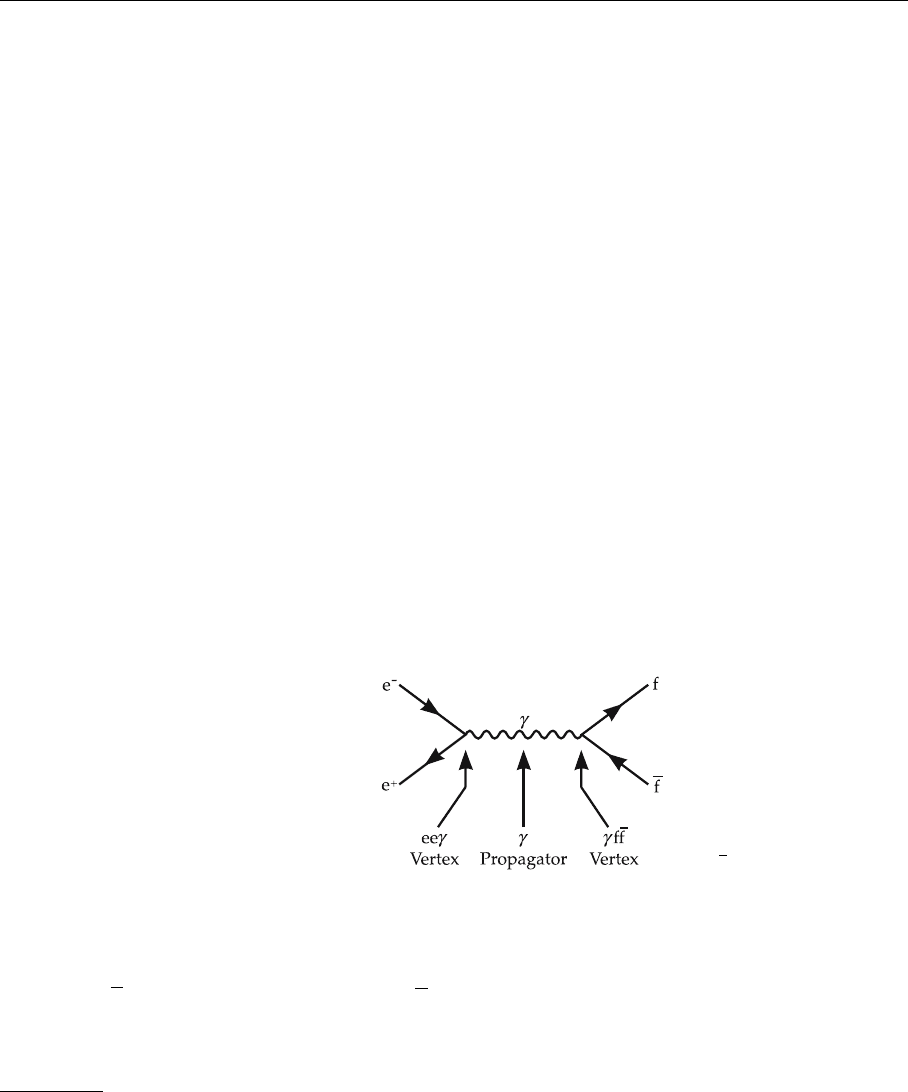
process is shown in the Feynman diagram in Figure 4.3, where f
¯
f can be a
quark-antiquark pair, a muon-antimuon pair, or any other fermion-antifermion
pair.
Fig. 4.3. The elementary
interaction graph for high
energy electron–positron an-
nihilation to a fermion-anti-
fermion pair, e
+
+e
−
→
f +
f
For a given choice of f
¯
f, the amplitude is found by multiplying three factors
for the vertices and the propagator, respectively. These factors are
e
+
e
−
γ vertex ,
−
√
α
γ propagator ,
1/W
γ f
¯
fvertex,
Q
f
√
α
where α is the fine structure constant, Q
f
is the electric charge of the fermion
f in units of the positron charge, and W is the total center-of-mass energy. Then
4
W. Greiner: Relativistic Quantum Mechanics – Wave Equations, 3rd ed. (Springer,
Berlin, Heidelberg 2000).
166 4. Gauge Theories and Quantum-Chromodynamics
the total amplitude A is proportional to the product, A ∼−Q
f
α/W, and the total
cross section, σ, is proportional to A
2
, hence σ ∼ Q
2
f
α
2
/W
2
. There are two more
factor missing in the cross section, a generic factor (4π/3) ·(hc)
2
,andN
c
,the
color factor. This last factor just counts all extra degrees of freedom the fermion-
antifermion pair can have. For colored quarks, it is the number of colors. Taking
everything together, the cross section for the creation of a muon-antimuon pair
is
σ(e
+
e
−
→µ
+
µ
−
) =
4π
3
α
2
W
2
, with Q
f
=−1, N
c
= 1 , (4.36)
and
σ(e
+
e
−
→uu) =
4π
3
2
3
2
N
c
α
2
W
2
, with Q
f
=+2/3, N
c
= 3
(4.37)
for a pair of up-antiup quarks. The cross section for the creation of all possible
quark-antiquark pairs is the sum over all quark-antiquark pairs,
σ(e
+
e
−
→all qq) =
4π
3
q
Q
2
q
N
c
α
2
W
2
, N
c
= 3 . (4.38)
Here we have put again h = c = 1, so that the (hc)
2
factors appearing in
these formulas also equal 1. If ff is a qq pair, then it is assumed that there is
a probability of 1 for becoming hadrons after the production of the q
q pair. Then
R =
σ(e
+
e
−
→hadrons)
σ(e
+
e
−
→µ
+
µ
−
)
=
q
Q
2
q
N
c
. (4.39)
Note that the cross sections are scale invariant and that these formulae apply only
if W 2m
f
.
Obviously the ratio of the cross sections is simply given by the charges of the
particles (provided the particle masses are negligible compared with the energy
of the e
+
e
−
pair). In detail one obtains:
R =
σ(e
+
e
−
→qq)
σ(e
+
e
−
→µ
+
µ
−
)
=
'
2
3
2
+
−1
3
2
+
−1
3
2
(
N
c
=
2
3
N
c
for E
cm
> 2GeV2m
u
, 2m
d
, 2m
s
,
R =
'
2
3
2
+
−1
3
2
+
−1
3
2
+
2
3
2
(
N
c
=
10
9
N
c
for E
cm
> 3GeV> 2m
c
, (4.40)
R =
'
2
3
2
+
−1
3
2
+
−1
3
2
+
2
3
2
+
−1
3
2
(
N
c
=
11
9
N
c
for E
cm
> 10 GeV > 2m
b
.
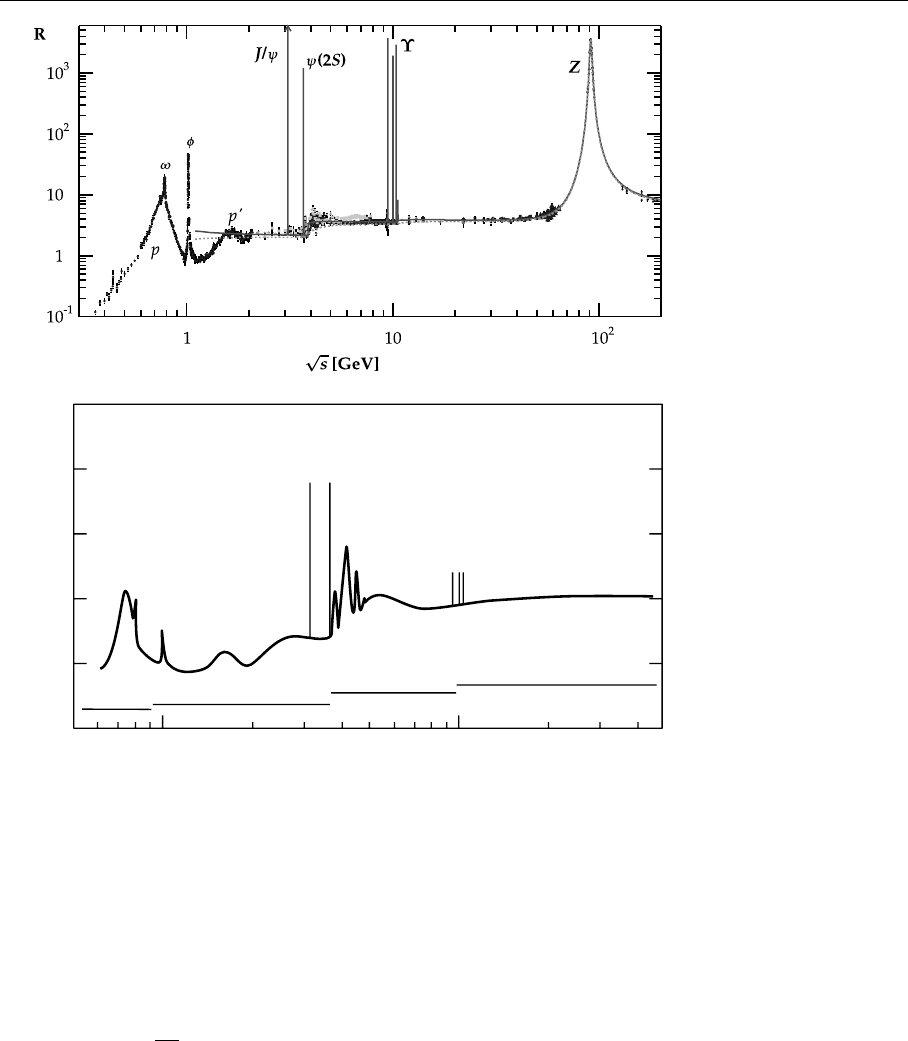
4.2 The Gauge Theory of Quark–Quark Interactions 167
Fig. 4.4a. The ratio of the
cross sections for hadronic
and muonic reactions in
e
+
e
−
pair annihilation,
R = σ(e
+
e
−
→hadrons)/
σ(e
+
e
−
→µ
+
µ
−
).From
S. Eidelman et al.: Review
of Particle Physics, Phys.
Lett. B 592, 1 (2004). Struc-
tures correspond to quark-
antiquark mesons and the Z
boson. A comparison with
theory including radiative
corrections is presented in
Fig. 7.15
10
8
6
4
2
R
0.6
0.8
12
46
8
10
20 30 40
2 (GeV)E
ud
uds
udsc
udscb
r
w
yy’
U’UU’’
f
Fig. 4.4b. The ratio R =
σ(e
+
e
−
→hadrons)/
σ(e
+
e
−
→µ
+
µ
−
)
as a function of the to-
tal center-of-mass energy
E
cm
= 2E (each beam has
energy E). The curve is
drawn through many meas-
ured points (see Fig. 4.4a)
and represents only a rough
average. However, it does
reproduce the major fea-
tures. The peaks are labelled
by the conventional sym-
bol representing the various
vector mesons. The nar-
row peaks due to the Ψ
and Υ families are inidcated
by vertival lines: the actual
values of the peak cross-
section are not represented.
The above B
¯
B-threshold Υ
states are ommited. The hor-
izontal lines marked with
quark flavours are the values
expected away from res-
onances and without the
colour factor N
c
Here N
c
denotes the number of colors. If we compare this prediction to the meas-
ured values (Fig. 4.4), it becomes clear that the assumptions made above lead to
the value N
c
=3. The second argument is quite similar. We consider the two-
photon decay of the π
0
meson shown in Fig. 4.5. Owing to the relatively small
pion mass only the u and d quarks contribute to this graph. The coupling to these
quarks is well understood from studies of the pion–baryon interaction, and the
decay width
Γ = 7.63 eV
N
c
3
2
(4.41)
is obtained. The experimental value
Γ
exp
= 7.57 ±0.32 eV (4.42)
