Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


188 4. Gauge Theories and Quantum-Chromodynamics
This relation is verified for integer d in Exercise 4.5. We note for later use that
in Exercise 4.5, (8), we also derive
∞
−∞
d
d
k e
−k
2
=
1
(d −2)!!
)
(2π)
d
2
d even
2 (2π)
d−1
2
d odd
*
∞
0
dkk
d−1
e
−k
2
. (4.71)
Now, for any function f(k) which can be expanded into Gaussians, i.e.
f(k) =
n
c
n
e
−A
n
(
k+p
n
)
2
, (4.72)
one obtains
∞
−∞
d
d
k
E
f(k
2
E
) =
1
(d −2)!!
)
(2π)
d
2
d even
2 (2π)
d−1
2
d odd
*
×
∞
0
dk
E
k
d−1
E
f(k
2
E
). (4.71b)
With Γ
1
2
=
√
π and the unifying relation
2(π)
d
2
Γ
d
2
=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
d even : 2π
d
2
×
2
d−2
×
2
d−4
×···×
2
2
=
(2π)
d
2
(d−2)!!
d odd : 2π
d
2
×
2
d−2
×
2
d−4
×···×
2
1
×
1
√
π
=
2(2π)
d−1
2
(d−2)!!
(4.73)
(4.71b) can be written as
∞
−∞
d
d
k
E
f(k
2
E
) =
2(π)
d
2
Γ
d
2
∞
0
dk
E
k
d−1
E
f(k
2
E
). (4.71c)
This equation is most important and will be used constantly during dimensional
regularization.

4.3 Dimensional Regularization 189
EXERCISE
4.5 The d-Dimensional Gaussian Integral
Problem. Derive (4.65) for integer d.
Solution. Omitting the subscript “E” in this exercise, we define for integer d
and Euclidian k
µ
, µ = 0, 1, 2,... ,d −1,
k
0
=k cos ϑ
1
,
k
1
=k sin ϑ
1
cos ϑ
2
,
k
2
=k sin ϑ
1
sin ϑ
2
cos ϑ
3
,
.
.
.
k
d−2
=k sin ϑ
1
sin ϑ
2
...sin ϑ
d−2
cos ϑ
d−1
,
k
d−1
=k sin ϑ
1
sin ϑ
2
...sin ϑ
d−2
sin ϑ
d−1
(1)
and calculate the Jacobian row by row
J =
∂(k
0
k
1
k
2
...k
d−1
)
∂(k,ϑ
1
,ϑ
2
...ϑ
d−1
)
=
cos ϑ
1
−k sin ϑ
1
0 ...
sin ϑ
1
cos ϑ
2
k cos ϑ
1
cos ϑ
2
−k sin ϑ
1
sin ϑ
2
...
sin ϑ
1
sin ϑ
2
cos ϑ
3
k cos ϑ
1
sin ϑ
2
cos ϑ
3
k sin ϑ
1
cos ϑ
2
cos ϑ
3
...
.
.
.
.
.
.
.
.
.
.
.
.
= k
d−1
$
cos ϑ
1
cos ϑ
1
(sin ϑ
1
)
d−2
+sin ϑ
1
sin ϑ
1
(sin ϑ
1
)
d−2
%
×
cos ϑ
2
−sin ϑ
2
...
sin ϑ
2
cos ϑ
3
cos ϑ
2
cos ϑ
3
...
.
.
.
.
.
.
.
.
.
= ...
= k
d−1
(sin ϑ
1
)
d−2
(sin ϑ
2
)
d−3
...(sin ϑ
d−3
)
2
×
cos ϑ
d−2
−sin ϑ
d−2
0
sin ϑ
d−2
cos ϑ
d−1
cos ϑ
d−2
cos ϑ
d−1
−sin ϑ
d−2
sin ϑ
d−1
sin ϑ
d−2
sin ϑ
d−1
cos ϑ
d−2
sin ϑ
d−1
sin ϑ
d−2
cos ϑ
d−1
= k
d−1
(sin ϑ
1
)
d−2
(sin ϑ
2
)
d−3
...(sin ϑ
d−2
)
×
cos ϑ
d−1
−sin ϑ
d−1
sin ϑ
d−1
cos ϑ
d−1
= k
d−1
(sin ϑ
1
)
d−2
(sin ϑ
2
)
d−3
...(sin ϑ
d−2
). (2)

190 4. Gauge Theories and Quantum-Chromodynamics
Exercise 4.5
The Gaussian integral thus becomes
∞
−∞
d
d
k e
−k
2
(3)
=
∞
0
dkk
d−1
e
−k
2
π
0
(sin ϑ
1
)
d−2
dϑ
1
...
π
0
sin ϑ
d−2
dϑ
d−2
π
0
dϑ
d−1
.
We use partial integration to get
π
0
(sin ϑ)
n−1
sin ϑ dϑ
=
(sin ϑ)
n−1
(−cos ϑ)
π
0
−(n −1)
π
0
(sin ϑ)
n−2
cos ϑ(−cos ϑ)dϑ
= (n −1)
π
0
(sin ϑ)
n−2
−(sin ϑ)
n
dϑ (4)
or
π
0
(sin ϑ)
n
dϑ =
n −1
n
π
0
(sin ϑ)
n−2
dϑ.
For even n ≥ 2 we thus get
π
0
(sin ϑ)
n
dϑ =
(n −1)!!
n!!
π
0
dϑ =
(n −1)!!
n!!
π, (5)
and for n = 0wehave
π
0
dϑ = π. (6)
For odd n we find
π
0
(sin ϑ)
n
dϑ =
(n −1)!!
n!!
π
0
sin ϑ dϑ
=
(n −1)!!
n!!
×2 . (7)

4.3 Dimensional Regularization 191
Inserting all these equations into (3) we get
∞
−∞
d
d
k e
−k
2
=
∞
0
dkk
d−1
e
−k
2
I
d
1
(d −2)!!
,
d even ⇒ I
d
= (2π)
d
2
,
d odd ⇒ I
d
= 2 ×(2π)
d−1
2
. (8)
On the other hand, partial integration gives
∞
0
dkk
d−1
e
−k
2
=
1
2
∞
0
dkk
d−2
2k e
−k
2
=
d −2
2
∞
0
dkk
d−3
e
−k
2
= (d −2)!!K
d
, (9)
d even ⇒ K
d
=
1
2
d−2
2
∞
0
dkke
−k
2
=
1
2
d
2
,
d odd ⇒ K
d
=
1
2
d−1
2
∞
0
dk e
−k
2
=
1
2
d−1
2
√
π
2
. (10)
All together this gives
∞
−∞
d
d
k e
−k
2
=
1
(d −2)!!
(d −2)!! I
d
K
d
=π
d
2
, (11)
which completes our proof.
With (4.67) all integrals can be expanded in a sum of Gaussians,
f(k) =
n
c
n
e
−A
n
(
k
E
+p
nE
)
2
, (4.74)
and f(k) can now be integrated d-dimensionally, i.e.
d
d
k
E
f(k
E
) =
n
c
n
A
−
d
2
n
π
d
2
. (4.71d)
However, it is not clear whether this sum converges. If it does for some integer
d, i.e., if the original integrand converges, then the expression (4.71d) also con-
verges. This is not true for divergent integrals. In this case the d-dimensional
Exercise 4.5

192 4. Gauge Theories and Quantum-Chromodynamics
integral may still be finite. Thus all finite parts of the momentum integrals are
reproduced. The infinite parts, associated, for example, with integrands like
1/(k
2
E
)
α
or (k
2
E
)
α
, which we want to subtract, will lead to infinite nonconvergent
sums over Gaussians, the resulting term on the right-hand side of (4.71b). These
will be subtracted during renormalization. We will see below that these infinite
parts are different for d-dimensional integrals than for normal ones. Actually
many divergences of usual integrals vanish automatically for d-dimensional in-
tegrals, and the important points to keep in mind throughout this discussion
are:
d-dimensional convergent integrals for d → n (where n is an integer) coincide
with the normal convergent n-dimensional integrals.
n-dimensional divergent integrals are in general different from the correspond-
ing d → n limit of the d-dimensional integral. The latter is in general less
divergent.
For example, for dimensional reasons the integral
d
d
k
1
k
2
+m
2
µ
(4.75)
behaves as (m
2
)
d/2−µ
. Thus for d =4 we will encounter a logarithmic di-
vergence for µ = 2, and a powerlike divergence for µ<2 which has to be
regularized by a cut-off in conventional n-dimensional integration. However, we
will show (see (4.81) below) that in dimensional regularization
d
d
k
1
k
2
+m
2
µ
∼ Γ(µ −d/2)(m
2
)
d/2−µ
(4.76)
does pick up only logarithmic divergences even for µ<2. For instance, for
µ = 1andd = 4 +2ε one gets
Γ(1 −2 −ε) = Γ(−1 −ε) =
−Γ(−ε)
1 +ε
=+(1 −ε)
1
ε
+γ
E
=
1
ε
+γ
E
−1 +O(ε) (4.77)
which clearly is only a (dimensionless) logarithmic divergence.
It is crucial to understand that our definition of a d-dimensional integral does
not always reduce to a normal integral in integer d dimensions. Instead it has
peculiar properties, for example,
d
d
k
E
k
2
E
ν
=0foranyν, (4.78)
which follows directly from the scaling axiom (4.66). Indeed we have
∞
−∞
d
d
k
E
λ
2
k
2
E
ν
=λ
2ν
∞
−∞
d
d
k
E
k
2
E
ν
=λ
−d
∞
−∞
d
d
k
E
k
2
E
ν
. (4.79)
4.3 Dimensional Regularization 193
Because this holds for any λ, ν, d, one is directly led to (4.78). Actually ν =−d/2
is the only power for which (4.78) does not imply the vanishing of this inte-
gral, but since we make critical use of the fact that our renormalized integrals
are analytic functions of all variables involved, like ν in(4.78),wehavealsoto
define
d
d
k
E
k
2
E
−
d
2
=0 . (4.80)
This derivation of (4.78) is actually not without problems, because it assumes
that
+
d
d
k
E
(k
2
E
)
ν
exists, which is only true after a specific definition such as
lim
m
2
→0
+
d
d
k
E
(k
2
E
+m
2
)
ν
. To be on the safe side it is better to regard (4.78) as
a definition that is made plausible by (4.65). A peculiar feature of (4.78) seems to
be that it leads to finite results even for theories for which arbitrarily high diver-
gences occur. While this is formally true it is of no importance since such theories
cannot be renormalized. They would require an infinite number of renormaliza-
tion constants and counterterms and thus cannot be formulated consistently. As
an example let us mention a scalar field theory with a φ
6
coupling. This coupling
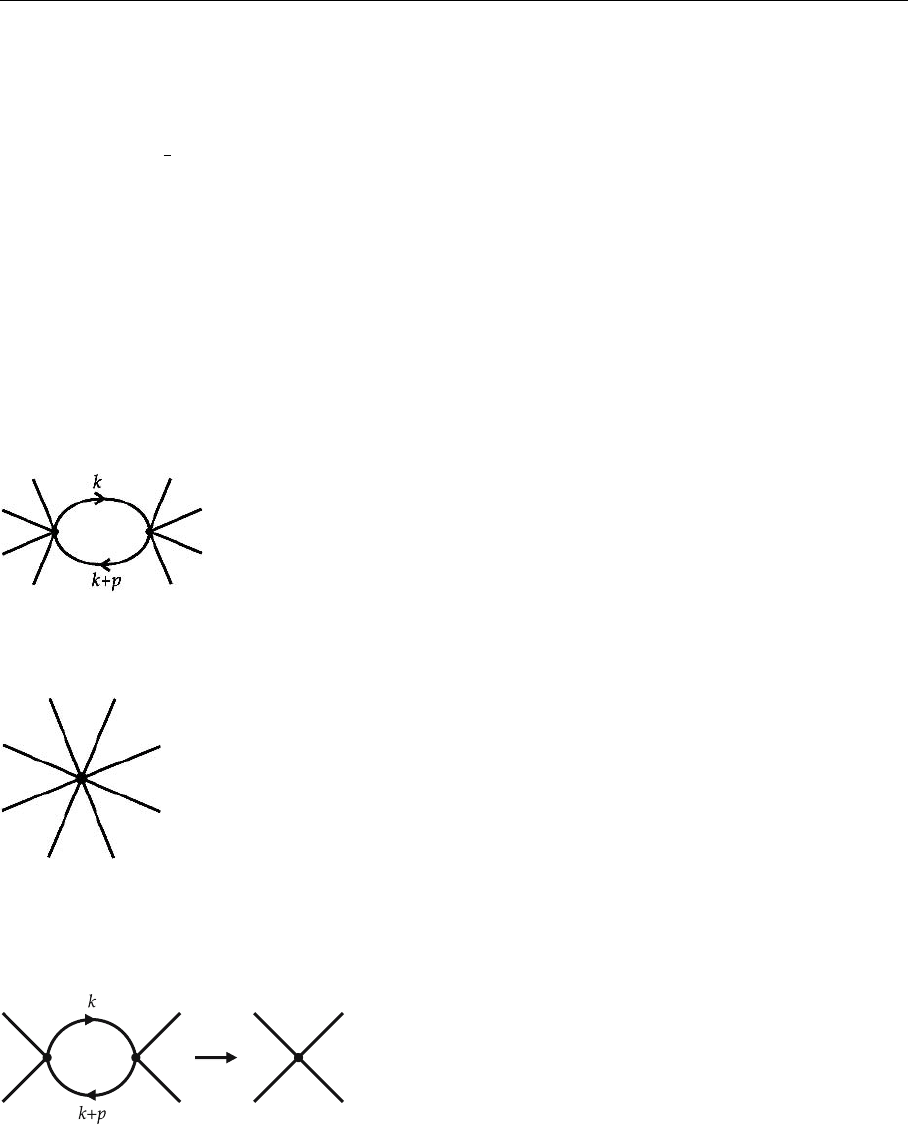
leads to divergent graphs like
which is divergent
∼
+
d
4
k
1/k
2
(k + p)
2
and must be renormalized, leading
to a counter term of the form
which is a φ
8
interaction. Continuing this argument we find that the renormalized
theory has infinitely many interaction terms of the general form
∞
n=3
c
n
φ
2n
,and
no consistent theory can be formulated. Note that for a φ
4
interaction
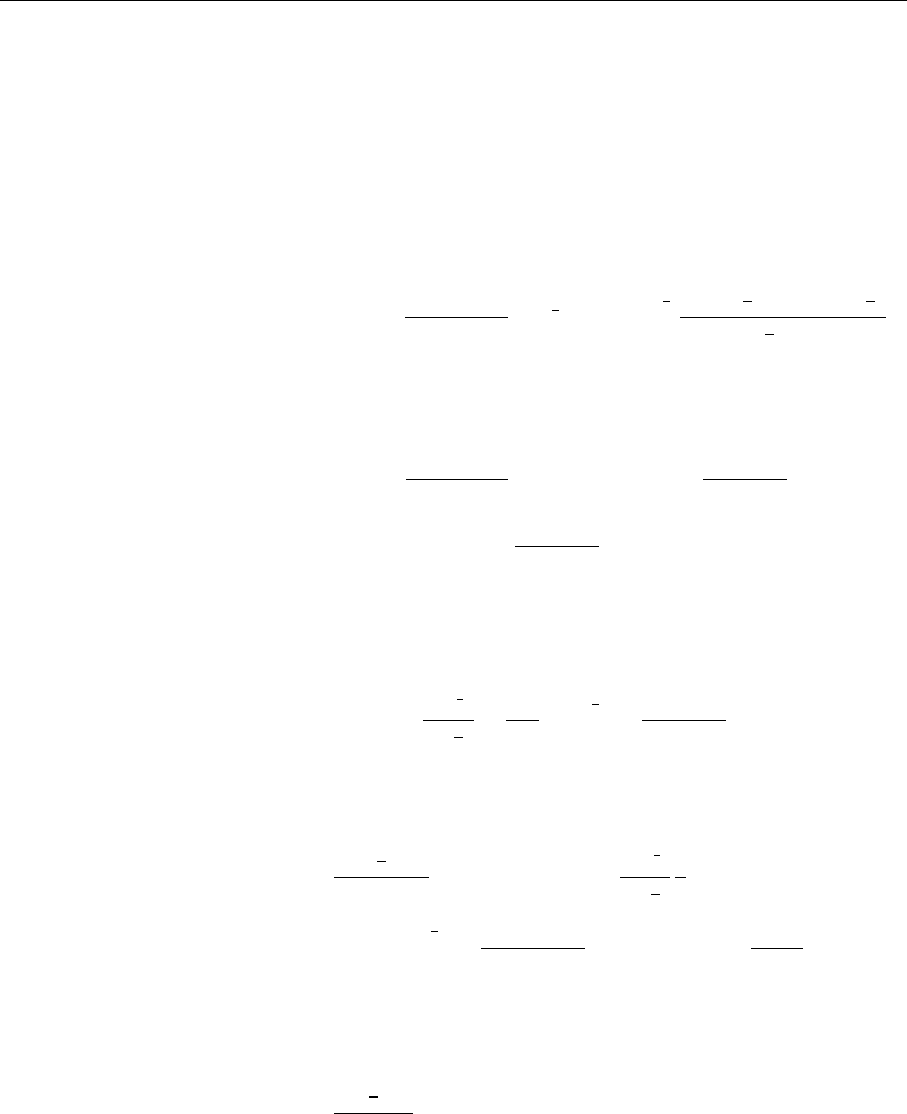
194 4. Gauge Theories and Quantum-Chromodynamics
the counterterm is again φ
4
. This is the reason why scalar theories up to φ
4
terms in the Lagrangian are renormalizable. In fact only those theories can be
renormalized that have at most logarithmic divergences, and thus integrals like
d
4
k
k
2
3
cannot occur. For renormalizable theories the differences between n-dimensional
integrals and d-dimensional integrals (with the limit d → n) is therefore
irrelevant.
Equation (4.78) is essential for deriving the following basic formula:
I
ν,µ
=
d
d
k
E
k
2
E
ν
k
2
E
+M
2
µ
= π
d
2
M
2
ν−µ+
d
2
Γ
ν +
d
2
Γ
µ −ν −
d
2
Γ
d
2
Γ(µ)
,
(4.81)
which we shall prove next. Using (4.78) we can rewrite I
ν,µ
in the following
manner:
I
ν,µ
=
d
d
k
E
k
2
E
ν
k
2
E
+M
2
µ
= M
2ν−2µ+d
d
d
k
E
k
2
E
ν
k
2
E
+1
µ
= M
2ν−2µ+d
d
d
k
E
'
k
2
E
ν
k
2
E
+1
µ
−
n
k
2
E
ν
n
c
n
(
(4.82)
with arbitrary constant coefficients ν
n
and c
n
. These coefficients are now chosen
such that they cancel all potential divergences, i.e., all high powers of k
2
.The
integral is then convergent and we simply apply (4.71c):
I
ν,µ
= M
2ν−2µ+d
2π
d
2
Γ
d
2
∞
0
dk
2
E
2
k
2
E
d
2
−1
'
k
2
E
ν
k
2
E
+1
µ
−
n
k
2
E
ν
n
c
n
(
.
(4.83)
The trick is now to derive by partial integration a recurrence relation for the I
ν,µ
:
I
ν,µ
=
ν +
d
2
−1
µ −1
I
ν−1,µ−1
+M
2ν−2µ+d
2π
d
2
Γ
d
2
1
2
×
)
k
2
E
ν+
d
2
−1
'
k
2
E
+1
1−µ
1 −µ
−
n
k
2
E
ν
n
+1−ν
c
n
ν
n
+1
(*
∞
0
.
(4.84)
The second term can obviously be absorbed into the c
n
s. In other words, c
n
can
be chosen such that it vanishes. This leaves us with the relation
I
ν,µ
=
ν +
d
2
−1
µ −1
I
ν−1,µ−1
for all real ν, µ . (4.85)

4.3 Dimensional Regularization 195
In view of the relation Γ(z +1) = zΓ(z), which uniquely defines the gamma
function, (4.85) suggests (d is fixed) the following ansatz for I
ν,µ
:
I
ν,µ
=
Γ
ν +
d
2
Γ(µ)
K(ν −µ) (4.86)
with an arbitrary function K(ν −µ).TofixK(ν −µ) we use the fact that
k
2
E
ν
k
2
E
+1
µ
=
k
2
E
ν
k
2
E
+1
µ
k
2
E
+1
−k
2
E
, (4.87)
I
ν,µ
= I
ν,µ−1
−I
ν+1,µ
. (4.88)
Inserting (4.86) into (4.88) gives
Γ
ν +
d
2
Γ(µ)
K(ν −µ) =
'
Γ
ν +
d
2
Γ(µ −1)
−
Γ
ν +
d
2
+1
Γ(µ)
(
K(ν −µ +1)
⇒ K(ν −µ) =
(µ −1) −
ν +
d
2
K(ν −µ +1)
=
µ −ν −1 −
d
2
K(ν −µ +1) (4.89)
⇒ K(ν −µ) = Γ
µ −ν −
d
2
const , (4.90)
where we have again used that the relation Γ(x +1) = xΓ(x) defines the gamma
function uniquely, up to a constant. The remaining constant in
d
d
k
E
k
2
E
ν
k
2
E
+M
2
µ
=
2π
d/2
Γ
d
2
M
2ν−2µ+d
Γ
µ −ν −
d
2
Γ
ν +
d
2
Γ(µ)
const (4.91)
can easily be fixed. We choose ν = 1 −d/2andµ = 2. With (4.71c) we get, on
the one hand,
∞
0
d
d
k
E
k
2
E
1−d/2
k
2
E
+M
2
2
=
2π
d/2
Γ
d
2
∞
0
dk
2
E
2
1
k
2
E
+M
2
2
=
2π
d/2
Γ
d
2
1
2
'
−1
k
2
E
+M
2
(
∞
0
=
π
d/2
Γ
d
2
1
M
2
(4.92)
and from (4.91), on the other hand,
2π
d/2
Γ
d
2
M
2−d−4+d
Γ
(
2 −1
)
Γ
(
1
)
Γ(2)
const =
2π
d/2
Γ
d
2
1
M
2
const . (4.93)

196 4. Gauge Theories and Quantum-Chromodynamics
Comparing both expressions we conclude that const =1/2, or
d
d
k
E
k
2
E
ν
k
2
E
+M
2
µ
=
π
d/2
Γ
d
2
M
2ν−2µ+d
Γ
µ −ν −
d
2
Γ
ν +
d
2
Γ(µ)
. (4.94)
This is an important formula, since any integral appearing in the calculations of
Feynman graphs can be brought into this form. The steps are:
(1) Introduce Feynman parameters according to
1
a
α
1
1
a
α
2
2
...a
α
m
m
=
Γ(α
1
+α
2
...α
m
)
Γ(α
1
)Γ(α
2
)...Γ(α
m
)
1
0
dx
1
x
1
0
dx
2
...
x
m−2
0
dx
m−1
×
x
α
1
−1
m−1
(x
m−2
−x
m−1
)
α
2
−1
...(1 −x
1
)
α
m
−1
[a
1
x
m−1
+a
2
(x
m−2
−x
m−1
) +...+a
m
(1 −x
1
)]
α
1
+α
2
...α
m
. (4.95)
This relation will be derived in Exercise 4.7.
(2) Shift the momentum variable of the loop k
µ
such that the linear term in the
denominator vanishes:
d
d
k
E
f(k
Eµ
)
k
2
E
+m
2
β
. (4.96)
(3) Use the fact that all k
µ
have to be contracted with some other k
λ
according to
k
µ
k
λ
→ g
µλ
k
2
/d. Otherwise the term vanishes if individual components k
µ
are
inverted, k
µ
→−k
µ
. The resulting expressions are sums of terms of the form
(4.94).
For convenience we give a list of expressions which shows the results from dif-
ferent terms following steps 2 and 3. The integrals on the left-hand sides are in
Minkowski space; therefore a factor “i” appears on the right, owing to the Wick
rotation.
d
d
k
1
k
2
+2k · p +m
2
α
=
iπ
d/2
m
2
− p
2
α−d/2
Γ
(
α −d/2
)
Γ(α)
. (4.97)
d
d
k
k
µ
k
2
+2k · p +m
2
α
=
iπ
d/2
m
2
− p
2
α−d/2
Γ
(
α −d/2
)
Γ(α)
(−p
µ
). (4.98)
d
d
k
k
2
k
2
+2k · p +m
2
α
=
iπ
d/2
m
2
− p
2
α−d/2
1
Γ(α)
Γ
α −
d
2
p
2
+Γ
α −1 −
d
2
d
2
m
2
− p
2
. (4.99)

4.3 Dimensional Regularization 197
d
d
k
k
µ
k
ν
k
2
+2k · p +m
2
α
=
iπ
d/2
m
2
− p
2
α−d/2
1
Γ(α)
Γ
α −
d
2
p
µ
p
ν
+Γ
α −1 −
d
2
1
2
g
µν
m
2
− p
2
. (4.100)
d
d
k
k
µ
k
ν
k
λ
k
2
+2k · p +m
2
α
=
iπ
d/2
m
2
− p
2
α−d/2
1
Γ(α)
−Γ
α −
d
2
p
µ
p
ν
p
λ
−Γ
α −1 −
d
2
m
2
− p
2
×
1
2
(g
µν
p
λ
+g
µλ
p
ν
+g
νλ
p
µ
)
. (4.101)
To check that (4.94) also reproduces (4.80) we use the following property of the
Γ function:
Γ(β +1) =βΓ(β)
⇒ lim
β→0
Γ(β) = lim
β→0
1
β
Γ(β +1)
= lim
β→0
1
β
1 +βΓ
(1) +O
β
2
=
1
β
+Γ
(1). (4.102)
This implies that
lim
µ→0
d
d
k
E
k
2
E
ν
k
2
E
+M
2
µ
= lim
µ→0
π
d/2
Γ
d
2
M
2ν+d
Γ
−ν −
d
2
Γ
ν +
d
2
µ = 0 . (4.103)
Equation (4.102) also allows us to write down in a uniform manner all the diver-
gences that can occur on the right-hand side of (4.94). Such divergences occur
if µ −ν −d/2orν +d/2 are negative integers or zero. The Γ function has no
zeros on the positive real axes, so that 1/Γ(µ) does not create any divergences.
With
lim
ε→0
Γ(−n +ε) = lim
ε→0
Γ(1 −n +ε)
−n +ε
= lim
ε→0
Γ(2 −n +ε)
(−n +ε)(1 −n +ε)
= ...
(4.104a)
all divergences can be related to lim
ε→0
Γ(ε) from (4.94). Let us discuss as an
example
lim
ε→0
Γ(−3 +ε) = lim
ε→0
Γ(ε)
(−3+ε)(−2 +ε)(−1 +ε)
= lim
ε→0
−
1
6
1 +
ε
3
+
ε
2
+ε
1
ε
+Γ
(1)
= lim
ε→0
−1
6ε
−
1
6
Γ
(1) +
1
3
+
1
2
+1
