Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

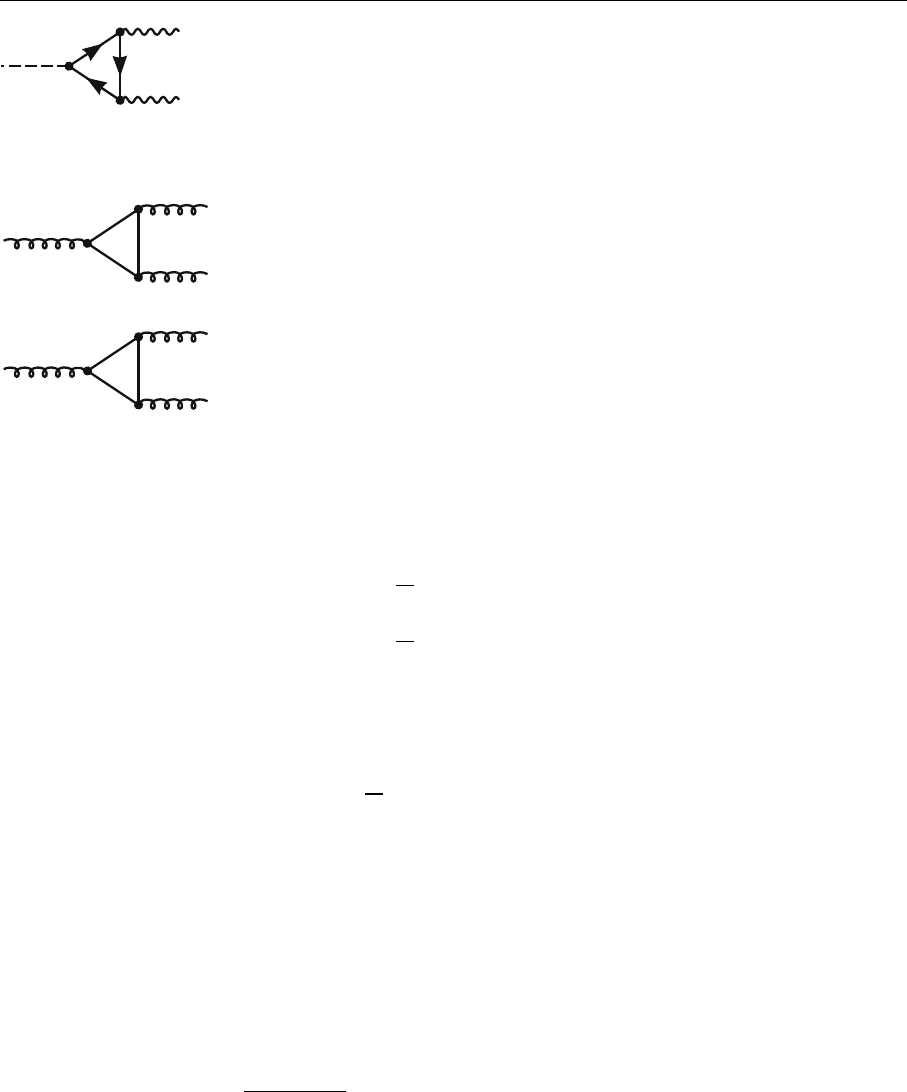
168 4. Gauge Theories and Quantum-Chromodynamics
π
γ
0
γ
Fig. 4.5. Graph for the
π
0
→2γ decay
+
-
l
i
gg
m 5
+
-
l
i
gg
m 5
g
l
l
j
gl
n
k
gg
l
k
g
l
n
j
Fig. 4.6. Potentially diver-
gent graphs of the standard
model. The plus holds for
right-handed fermions and
the minus sign for left-
handed fermions. The upper
and lower diagrams differ in
the exchange of the outgoing
gluons.
obviously again favors N
c
= 3. As some theoretical assumptions enter the
derivation of (4.37), this argument is somewhat less direct than the first one.
The last argument we want to discuss is of a purely theoretical nature. From
a strictly empirical point of view it is therefore the least well founded. From the
theoretical point of view it is, on the contrary, the most fascinating, since it states
that the standard model is only internally consistent for three colors. This implies
that there must be a fundamental symmetry linking the electroweak sector of the
standard model to the QCD sector and thus motivates the search for a Grand
Unified Theory.
In the last section we claimed that all gauge theories with or without spon-
taneous symmetry breaking are renormalizable. However, this statement is not
valid in full generality, since there are graphs in the standard model, for example,
that are divergent and not subject to the general proof of renormalizability. They
can all be traced to the triangle anomaly, which is discussed in detail in Gauge
Theory of Weak Interactions.
5
In essence the anomaly can be reduced to the
time-ordered product of one axial vector current and two vector currents:
T
ijk
µνλ
(k
1
, k
2
, q) = i
dx
1
dx
2
exp
(
ik
1
·x
1
+ik
2
·x
2
)
0 | A
i
µ
(x
1
)V
k
ν
(x
2
)V
j
λ
(0) | 0 , (4.43)
as depicted in Fig. 4.6. The currents are
A
i
µ
(x) =
¯
ψ(x)
ˆ
λ
i
2
γ
µ
γ
5
ψ(x),
V
i
µ
(x) =
¯
ψ(x)
ˆ
λ
i
2
γ
µ
ψ(x). (4.44)
In the standard model there exist chiral fermions that exhibit vector (γ
µ
) as well
as axial vector (γ
µ
γ
5
) character, which can be seen by considering the weak
current of the GSW theory
J
i
µ
∼
¯
ψ(x)
ˆ
λ
i
2
(1 ±γ
5
)γ
µ
ψ(x). (4.45)
Since for right- and left-handed fermions γ
5
enters with different sign they
contribute with opposite sign to the anomalous triangle diagram. Left-handed
fermions are members of the doublet representation,
ˆ
λ
i
, thus denoting the
SU
L
(2) ×U
Y
(1) 2 ×2 matrices, being essentially the three Pauli matrices
ˆ
τ
i
plus the unit matrix. The latter is proportional to the hypercharge. Right-handed
fermions are members of the singlet representation. Thus in the right-handed
case the
ˆ
λ
i
reduce to a single number, being the hypercharge of the right-handed
fermion. We shall now demonstrate that the quark and lepton contributions to the
triangle diagram cancel exactly. When calculating the diagram we have to take
the trace of the
ˆ
λ matrices and take into account the exchange diagram. The result
5
W. Greiner and B. Müller: Gauge Theory of Weak Interactions, 3rd ed. (Springer,
Berlin, Heidelberg 2000).

4.2 The Gauge Theory of Quark–Quark Interactions 169
is proportional to
tr
ˆ
λ
i
ˆ
λ
j
ˆ
λ
k
+tr
ˆ
λ
i
ˆ
λ
k
ˆ
λ
j
= tr
ˆ
λ
i
{
ˆ
λ
j
,
ˆ
λ
k
}
. (4.46)
Let us first investigate the doublet contributions to the left-handed fermions. For
pure SU
L
(2) the corresponding coeficient vanishes:
tr
ˆ
τ
i
{
ˆ
τ
j
,
ˆ
τ
k
}
= 2δ
jk
tr
ˆ
τ
i
= 0 . (4.47)
The same is the case if two of the
ˆ
λ matrices are the hypercharge:
tr
ˆ
τ
i
{
ˆ
Y,
ˆ
Y}
=2
ˆ
Y
2
tr
ˆ
τ
i
= 0 . (4.48)
Thus we have to consider only those cases in which one or all of the
ˆ
λ matrices
are the hypercharge
ˆ
Y.Wehave
tr
ˆ
Y{
ˆ
τ
j
,
ˆ
τ
k
}
=2δ
jk
tr
ˆ
Y
, (4.49)
and thus the anomaly contribution is proportional to Y. Summing over all
doublets of one generation we arrive at
doublets
Y =
lh. quarks
Y +
lh. leptons
Y , (4.50)
which vanishes by explicit calculation for the fermion assignments in each
generation, as can be read off from Table 4.1. Indeed one has
lh. quarks
Y = 3
1
3
×2
=2 ,
lh. leptons
Y =−1 ×2 =−2 . (4.51)
The factor 3 in the sum over left-handed quarks is due to the color degree of
freedom. For the case when all
ˆ
λ matrices are the hypercharge we find that the
potentially anomalous contribution has a coefficient given by
tr
ˆ
Y
ˆ
Y
ˆ
Y
∼Y
3
. (4.52)
Now we have to consider also contributions of the right-handed singlets which
enter with opposite sign:
lh. quarks
Y
3
−
rh. quarks
Y
3
=3
1
3
3
×2 −
'
4
3
3
+3
−2
3
3
(
=−6 ,
lh. leptons
Y
3
−
rh. leptons
Y
3
=(−1)
3
×2 −(−2)
3
= 6 . (4.53)
If there are exactly three times as many quarks as leptons their contributions can-
cel exactly, i.e. the large loop momenta do not contribute to the graphs in Fig. 4.6,
which then are no longer divergent. Assuming in addition that there are just as
many kinds of leptons as quark flavors, we conclude that there must exist three
colors.

170 4. Gauge Theories and Quantum-Chromodynamics
T T
3
y Q
ν
e
+
1
2
+
1
2
−1 +0
e
L
+
1
2
−
1
2
−1 −1
e
R
+0 +0 −2 −1
u
L
+
1
2
+
1
2
+
1
3
+
2
3
(d
C
)
L
+
1
2
−
1
2
+
1
3
−
1
3
u
R
+0 +0 +
4
3
+
2
3
(d
C
)
R
+0 +0 −
2
3
−
1
3
Table 4.1. The quantum
numbers of the particles of
the first fermion family of
the standard model
This argument might have a problem, since the graphs of Fig. 4.6 might be
renormalizable in the context of an improved field theory or in a theory going far
beyond field theory. We know, however, that they cannot be renormalized on the
basis of the present understanding and with any technique developed so far. The
role of the anomaly is so fascinating just because it seems to point to something
beyond the standard model. It has several very interesting consequences; for ex-
ample, owing to the anomaly, the standard model should violate separate lepton
and baryon number conservation, conserving only B–L, which again shows that
it is intimately connected with any unifying model.
Altogether the arguments discussed are sufficiently convincing to demand
that every theory of quark–quark interactions has to start with three color states.
In analogy to the standard model it is quite natural to regard them as the fun-
damental representation of a SU(3) color group. It is actually relatively easy to
see that SU(3) is the only possible compact semi-simple Lie group. These Lie
groups are completely classified and one can look up their irreducible represen-
tations in, for example, R. Slansky, Phys. Rep. 79, p. 1–128. SU(3) is the only
group which has complex irreducible triplets. The only alternative to standard
QCD are, therefore, groups that are spontaneously broken to a SU(3) symmetry
group plus some high mass residues of the original, larger group. Consequently
the basic equations are just (4.6) and (4.7), where we have changed the sign of g
and
ˆ
θ(x) in order to agree with common conventions:
ˆ
A
ν
(x) =
8
a=1
1
2
ˆ
λ
a
A
a
ν
(x)(
ˆ
λ
a
=SU(3) matrices),
ˆ
θ(x) =
8
a=1
1
2
ˆ
λ
a
θ
a
(x), (4.54)
and
ˆ
A
ν
(x) →
ˆ
A
ν
(x) = e
ig
¯
θ(x)
¯
A
ν
(x) +
i
g
∂
ν
e
−ig
¯
θ(x)
,
Ψ(x) →Ψ
(x) = e
ig
ˆ
θ(x)
Ψ(x). (4.55)
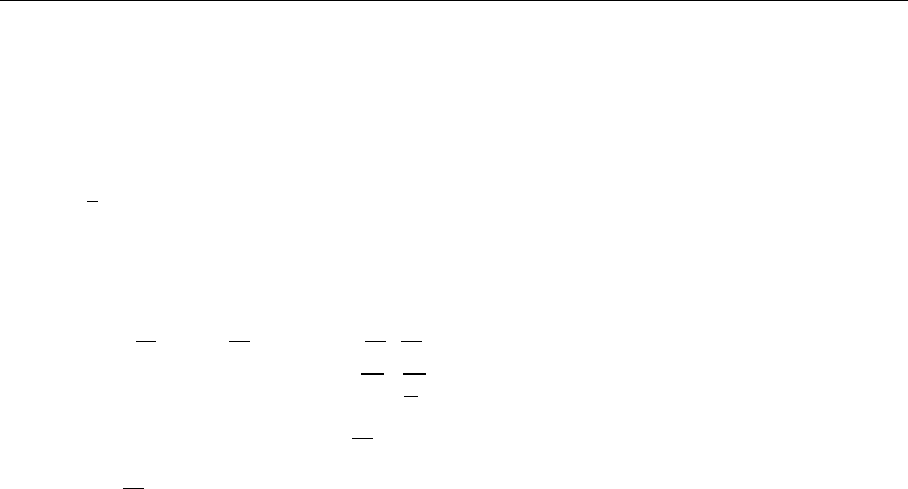
4.2 The Gauge Theory of Quark–Quark Interactions 171
The quark wave function is then a color-SU(3) triplet
Ψ(x) =
⎛
⎝
Ψ
r
(x)
Ψ
b
(x)
Ψ
g
(x)
⎞
⎠
(4.56)
and the Lagrangian is
L =−
1
2
tr(
ˆ
F
µν
ˆ
F
µν
) +
¯
Ψ(p
µ
+g
ˆ
A
µ
)γ
µ
Ψ (4.57)
with the tensor of the gluon field strength
ˆ
F
µν
=∂
µ
ˆ
A
ν
−∂
ν
ˆ
A
µ
−ig
ˆ
A
µ
,
ˆ
A
ν
=∂
µ
A
a
ν
λ
a
2
−∂
ν
A
a
µ
λ
a
2
−igA
a
µ
A
b
ν
λ
a
2
,
λ
b
2
7
89 :
i f
abc
λ
c
2
=
∂
µ
A
a
ν
−∂
ν
A
a
µ
+gf
abc
A
b
µ
A
c
ν
λ
a
2
≡ F
a
µν
λ
a
2
. (4.58)
Equations (4.54) to (4.58) completely define the theory. They lead to the Feyn-
man rules and allow the evaluation of arbitrary graphs. This procedure has been
very successful for all field theories discussed so far, but in the case of QCD it has
to be applied with care. Here the essential question is under what circumstances
does such a perturbative expansion in the coupling constant, as Feynman rules
imply, converge. One finds that the smallness of the coupling constant is an in-
sufficient criterion. It is still not completely understood, for example, whether
the perturbative treatment of QED really converges or whether this is only an
asymptotic expansion. In the latter case the evaluation of additional classes of
graphs would yield improvements only to a certain order in α. The consideration
of higher-order terms then would again worsen the agreement with experimental
observations. Unfortunately the QCD coupling constant has to be chosen in such
a way that the convergence of the resulting perturbation series is not clear. To be
more precise the convergence depends on the value of the momenta that occur.
In the case of large momenta, for example, in deep inelastic electron–nucleon
scattering reactions, we shall show that perturbative calculations agree very well
with experimental results. But for small momenta no convergence can be ob-
served; see the discussion of the running coupling constant in Example 4.4. This
fact, however, fits quite well into the general picture, since quark confinement,
for instance, is supposed to be a nonperturbative effect. To what extent is this
behavior characteristic for the SU(3) theory? In fact only the way in which g de-
creases with increasing momentum is typical for the SU(3) theory. An SU(4) or
SU(2) theory would lead to a stronger or weaker dependence, respectively. For
a U(1) theory, e.g., QED, even the opposite behavior occurs. Here perturbation
theory converges very well at small momenta and breaks down at unphysically
high scales (of the order of 10
20
GeV).

172 4. Gauge Theories and Quantum-Chromodynamics
kb,,n
pi,,g
pj
', ,b
General features are thus not necessarily characteristic for the chosen theory.
Only a thorough and detailed analysis of many processes with different momen-
tum transfers can prove the validity of the QCD equations (4.49)–(4.53). The
completion of such an analysis is still out of sight, but the evidence in favor of an
SU(3) color gauge theory is meanwhile so strong that at present hardly anybody
seriously doubts its validity.
Before we turn in the next chapter to perturbative QCD for large momen-
tum transfers, Example 4.2 introduces the Feynman rules for QCD. Finally,
Example 4.3 gives more details on the dependence of the coupling constant on
momentum transfer.
EXAMPLE
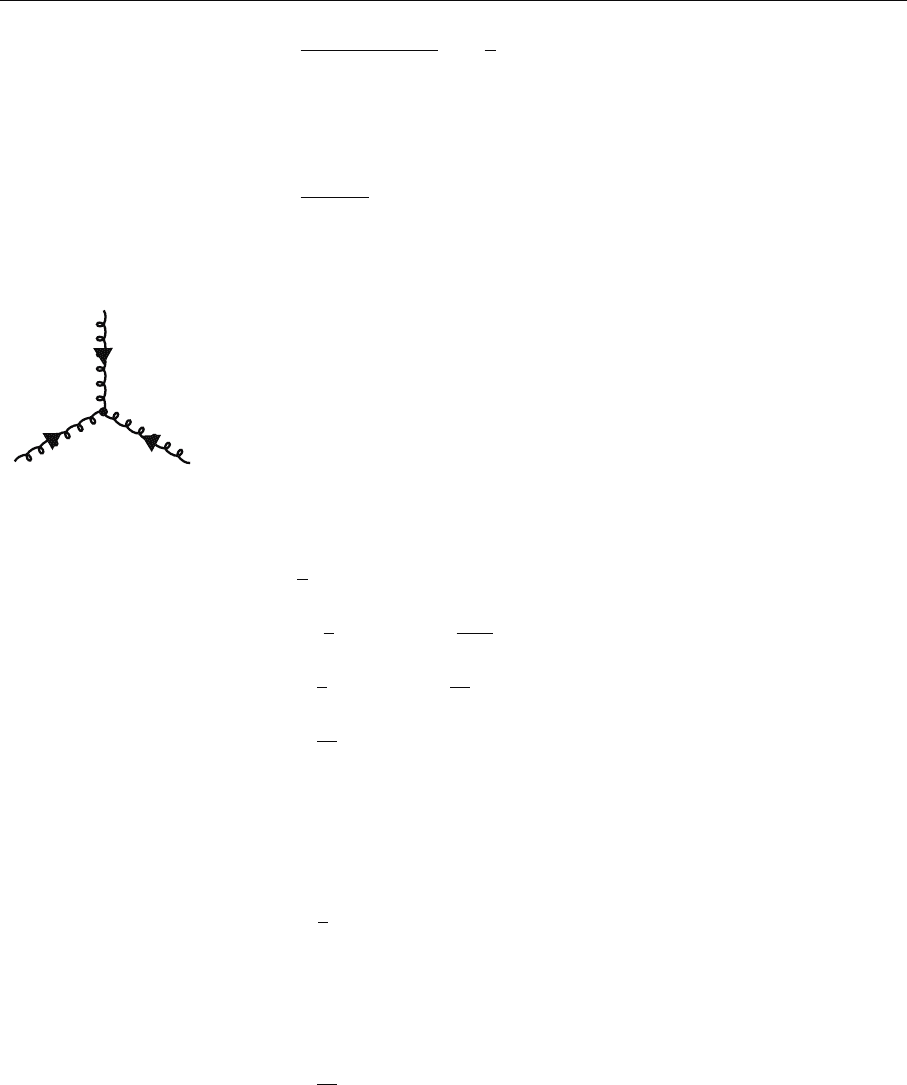
4.2 The Feynman Rules for QCD
First we discuss the vertices, starting with the quark–gluon vertex, which can be
deduced from the following part of the Lagrangian:
L
int
=
¯
Ψ g
λ
a
2
γ
µ
A
aµ
Ψ. (1)
Throughout this problem latin letters a, b, c,... denote the SU(3) index. One has
to sum over indices occurring twice (a = 1,... ,8).
In general, Feynman rules are obtained by varying the corresponding action
integral in momentum space. Here
δ
3
δΨ
i
γ
( p)δ
¯
Ψ
j
β
( p
)δA
bν
(k)
¯
Ψ(p
1
)g
λ
a
2
γ
µ
A
aµ
( p
2
)Ψ( p
3
)
×(2π)
4
δ
4
( p
1
+ p
2
− p
3
) d
4
p
1
d
4
p
2
d
4
p
3
(2)
has to be evaluted. Using
δΨ( p
1
)
i
γ
δΨ( p
)
j
β
= δ
4
( p
1
− p
)δ
ij
δ
γβ
, etc. (3)
we can simplify the quark–gluon vertex to
g
λ
b
2
ji
(γ
ν
)
βγ
(2π)
4
δ
4
( p
+k − p). (4)
Since the gauge field is non-Abelian, the gluon Lagrangian also contains second
and third powers of the field
ˆ
A
µ
, which lead to gluon–gluon interactions.
The three-gluon vertex is evaluted in an analogous way. From the Lagrangian
we obtain, with
tr
λ
a
λ
b
,λ
c
= 2i f
bcd
tr
λ
a
λ
d
=4i f
abc
, (5)

4.2 The Gauge Theory of Quark–Quark Interactions 173
the following three-gluon terms:
−
1
2
tr
ˆ
F
µν
ˆ
F
µν
=−
1
2
tr
#
F
a
µν
F
µνb
λ
a
2
λ
b
2
&
=−
1
8
F
a
µν
F
µνb
tr
λ
a
λ
b
=−
1
4
F
a
µν
F
µνa
=−
1
4
∂
µ
A
a
ν
−∂
ν
A
a
µ
gf
abc
A
bµ
A
cν
+gf
abc
A
b
µ
A
c
ν
∂
µ
A
νa
−∂
ν
A
µa
+...
=−
g
2
∂
µ
A
a
ν
−∂
ν
A
a
µ
f
abc
A
bµ
A
cν
+...
−g∂
µ
A
a
ν
f
abc
A
bµ
A
cν
. (6)
In the last step
∂
µ
A
a
ν
−∂
ν
A
a
µ
=−
∂
ν
A
a
µ
−∂
µ
A
a
ν
and f
abc
=−f
acb
have
been used. The dots ... indicate noncubic terms.
Again this is transformed into momentum space and varied with respect to
the fields:
δ
3
δA
r
(k
1
)δA
s
σ
(k
2
)δA
t
τ
(k
3
)
×
#
−
g
2
i p
1,µ
A
a
ν
( p
1
) −i p
1,ν
A
a
µ
( p
1
)
f
abc
A
bµ
( p
2
)
× A
cν
( p
3
)(2π)
4
δ
4
( p
1
+ p
2
+ p
3
) d
4
p
1
d
4
p
2
d
4
p
3
&
=
δ
2
δA
r
(k
1
)δA
s
σ
(k
2
)
#
−i
g
2
k
3,µ
f
tbc
A
bµ
( p
2
)A
cτ
( p
3
)
(2π)
4
δ
4
(k
3
+ p
2
+ p
3
) d
4
p
2
d
4
p
3
+i
g
2
k
3,ν
f
tbc
A
bτ
( p
2
)A
cν
( p
3
)
(2π)
4
δ
4
(k
3
+ p
2
+ p
3
) d
4
p
2
d
4
p
3
−i
g
2
p
1,µ
A
a
ν
( p
1
) − p
1,ν
A
a
µ
( p
1
)
f
abc
δ
b
t
g
µτ
A
b,µ
( p
3
)
(2π)
4
δ
4
(k
3
+ p
1
+ p
3
) d
4
p
2
d
4
p
3
−i
g
2
p
1,µ
A
a
ν
( p
1
) − p
1,ν
A
a
µ
( p
1
)
f
abc
δ
c
t
g
ντ
A
c,ν
( p
2
)
(2π)
4
δ
4
(k
3
+ p
1
+ p
2
) d
4
p
1
d
4
p
2
&
Example 4.2
174 4. Gauge Theories and Quantum-Chromodynamics
Example 4.2
k
1
,n, r
kt
3
, ,t
ks,
2
, s
=
δ
2
δA
r
(k
1
)δA
s
σ
(k
2
)
#
−i
g
2
k
3,µ
f
tbc
A
bµ
( p
2
)A
cτ
( p
1
)
−k
3,ν
f
tbc
A
bτ
( p
1
)A
cν
( p
2
) +2 f
tca
A
cν
( p
1
)
p
2
τ
A
a
ν
( p
2
)
− p
2,ν
A
aτ
( p
2
)
(2π)
4
δ
4
( p
1
+ p
2
+k
3
) d
4
p
1
d
4
p
2
&
=
δ
δA
r
(k
1
)
(−ig)
k
3,µ
f
tbs
A
bµ
( p)g
στ
+k
3
σ
f
tsc
A
cτ
( p)
+ f
tsa
p
τ
A
aσ
( p) − p
σ
A
aτ
( p)
+k
2
τ
f
tcs
A
cσ
( p)
−k
2,ν
f
tcs
A
cν
( p)g
τσ
(2π)
4
d
4
( p +k
2
+k
3
)d
4
p
=−ig
k
3
f
trs
g
στ
+k
3
σ
f
tsr
g
τ
+ f
tsr
k
1
τ
g
σ
−k
1
σ
g
τ
+ f
trs
k
2
τ
g
σ
−k
2
g
τσ
(2π)
4
δ
4
(k
1
+k
2
+k
3
)
= igf
rst
k
1
τ
−k
2
τ
g
σ
+
k
2
−k
3
g
στ
+
k
3
σ
−k
1
σ
g
τ
(2π)
4
δ
4
(k
1
+k
2
+k
3
). (7)
Also the four-gluon vertex can be determined in the same manner. Using (4.53),
the relevant part of the Lagrangian is
−
1
2
tr
ˆ
F
µν
ˆ
F
µν
→−
1
2
A
e
µ
A
f
ν
A
rµ
A
sν
−g
2
16
tr
λ
e
,λ
f
λ
r
,λ
s
=−
1
2
A
e
µ
A
f
ν
A
rµ
A
sν
g
2
4
tr
$
λ
g
λ
t
%
f
efg
f
rst
=−
g
2
4
f
efg
f
rsg
A
e
µ
A
f
ν
A
rµ
A
sν
. (8)
Here the well-known relations
λ
e
,λ
f
−
=i2 f
efg
λ
g
and tr
$
λ
g
λ
t
%
=2δ
gt
have
been applied. Performing the standard transformation to momentum space sim-
ply yields all possible permutations of the four index pairs (a,α), (b,β), (c,γ),
and (d,δ), i.e., a total of 4!=24 terms:
−
1
4
g
2
f
efg
f
rsg
δ
ae
δ
bf
δ
cr
δ
ds
g
αγ
g
βδ
+δ
ae
δ
bf
δ
cs
δ
dr
g
αδ
g
βγ
+δ
ae
δ
br
δ
cf
δ
ds
g
αβ
g
γδ
+δ
ae
δ
br
δ
cs
δ
df
g
αβ
g
γδ
+δ
ae
δ
bs
δ
cr
δ
df
g
αγ
g
βδ
+δ
ae
δ
bs
δ
cf
δ
dr
g
αδ
g
βγ
+(e →r, f → s) +(e → f, r → s) +(e → s, f → r)
=−
g
2
4
f
gab
f
gcd
g
αγ
g
βδ
−g
αδ
g
βγ
+ f
gac
f
gdb
g
αδ
g
βγ
−g
αβ
g
γδ
+ f
gad
f
gbc
g
αβ
g
γδ
−g
αγ
g
βδ
4 . (9)
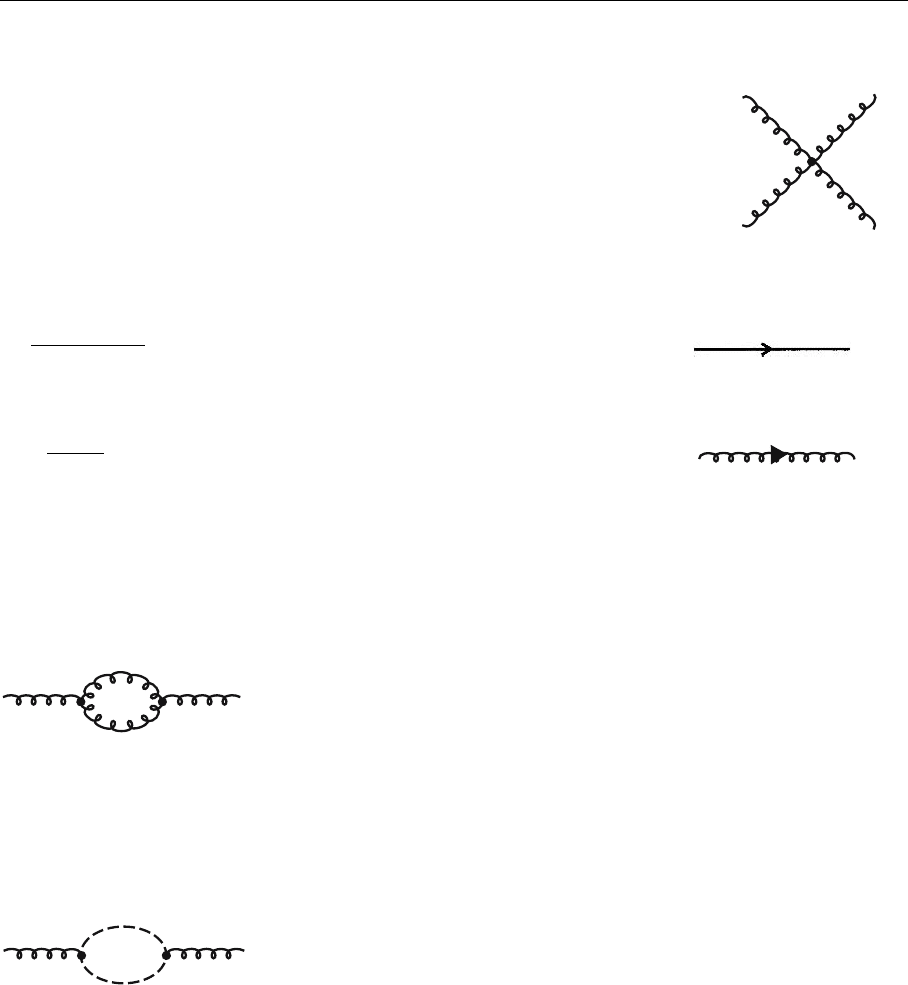
4.2 The Gauge Theory of Quark–Quark Interactions 175
Because of the permutation relations concerning f
efg
f
rsg
,thethreetermsde-
noted by (e →r, f → s), etc. contribute the same as the first one. The complete
vertex factor is then
−g
2
f
eab
f
ecd
g
αγ
g
βδ
−g
αδ
g
βγ
+ f
eac
f
edb
g
αδ
g
βγ
−g
αβ
g
γδ
+f
ead
f
ebc
g
αβ
g
γδ
−g
αγ
g
βδ
×(2π)
4
δ
4
(k
1
+k
2
+k
3
+k
4
). (10)
In principle the propagators are identical with those in QED. Hence the quark
propagator is
1
p ·γ −m +iε
(11)
and the gluon propagator could be chosen to be
−
g
µν
δ
ab
k
2
+iε
. (12)
In QED the rule holds that outer lines only propagate real physical degrees of
freedom, in particular transverse photons. On the other hand, inner lines (those
occurring in loops) represent all degrees of freedom. The latter is possible be-
cause the nonphysical components do not contribute to closed loops. However, in
QCD additional vertices occur resulting in additional loops that no longer exhibit
this feature, e.g.
Therefore one has for every inner line to subtract the nonphysical gluonic
contributions. This can be achieved by introducing an artificial particle with-
out any physical meaning. The couplings and the propagator of this particle are
chosen in such a way that graphs containing this particle cancel the nonphysical
gluonic contributions. The corresponding graph is
Here the dashed line denotes the new particle just mentioned. Because of their
nonphysical nature these particles are called “ghosts” or “ghost fields”. We shall
not discuss here how these fields are exactly defined and how their couplings are
determined. We only list the corresponding Feynman rules. Example 4.3 may
help us to understand the ghost idea somewhat better.
Example 4.2
k,a
1
,a
1
k,b
2
,b
k,d
4
,d
k,c
3
,g
a,mn
,b
176 4. Gauge Theories and Quantum-Chromodynamics
Example 4.2
One should be aware of the “i” in the expression for the vertex. This differ-
ent phase compared with (7) shows that certain cancellations of ghost and gluon
loops are possible. In that way, if the expression (21) below is implemented twice
in the above ghost-loop diagram, additional “i” results in a minus-sign, so that
the ghost-loop amplitude
partly cancels the gluon-loop amplitude
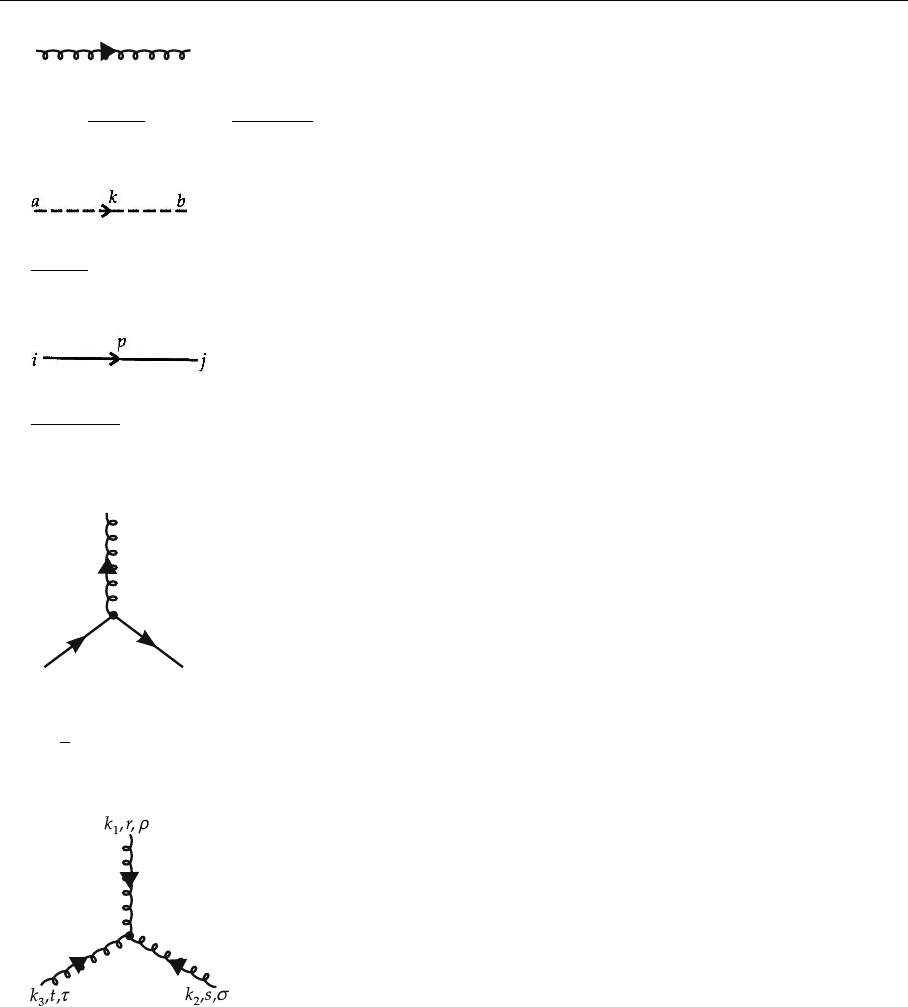
The Feynman rules discussed above are summarized in (15)–(21). In order
to indicate the different possible gauges, the gluon propagator is given in its
most general form, assuming ∂
µ
A
µ
=0 (transverse gauge). From QED we al-
ready know the Landau gauge (λ = 1) and the transverse propagator (λ → 0).
In fact an arbitrary mixing of these two cases can also be chosen. Gauge invari-
ance implies that in the evaluation of a physical process all λ-dependent terms
cancel each other or are equal to zero. Therefore λ can be arbitrarily chosen, i.e.
different from λ =1,λ→ 0:
m,,ak
cq
,
bp,
−igf
abc
p
µ
(2π)
4
δ
4
( p −k −q) (13)
and
i
j
δ
ij
p
2
+iε
(14)
Note that all Feynman graphs are frequently multiplied by an additional factor i
because the starting point of a perturbative expansion is really i
+
L(x) d
4
x and
not
+
L(x) d
4
x. However, this leads only to an unimportant overall phase.
4.2 The Gauge Theory of Quark–Quark Interactions 177
k
a
,m
b,n
−δ
ab
g
µν
k
2
+iε
−(1 −λ)
k
µ
k
ν
(k
2
+iε)
2
, (15)
δ
ab
k
2
+iε
, (16)
δ
ij
p/ −m +iε
, (17)
kb,,n
pi,,
g
pj', ,b
g
1
2
λ
b
ji
(γ
ν
)
βγ
(2π)
4
δ
4
( p
+k − p), (18)
igf
rst
k
τ
1
−k
τ
2
g
σ
+
k
2
−k
3
g
στ
+
k
σ
3
−k
σ
1
g
τ
(2π)
4
δ
4
(k
1
+k
2
+k
3
), (19)
Example 4.2
