Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

198 4. Gauge Theories and Quantum-Chromodynamics
=−
Γ
(1) +
11
6
6
−
1
6
lim
ε→0
1
ε
. (4.104b)
All possible divergences (which can be only logarithmic for renormalizable
theories) are therefore proportional to 1/ε, and (4.94) and (4.104a,b) already
determine dimensional regularization.
Dimensional regularization, i.e., the separation of the divergent and finite
parts, is realized by identifying the 1/ε terms with the divergent part and the rest,
which is the finite one. The 1/ε terms are then absorbed into the renormalization
constants, such as mass, charge, ..., during renormalization.
To end this section, let us mention a second valuable formula for dimensional
regularization (d = 4 +2ε):
d
d
x
e
i p·x
(−x
2
)
ν
=−iπ
2
Γ(2 −ν +ε)
Γ(ν)
−4π
2
µ
2
p
2
ε
−p
2
4
ν−2
, (4.105)
which allows us to perform d-dimensional Fourier transformations. It is derived
in Exercise 4.6.
EXERCISE
4.6 The d-Dimensional Fourier Transform
Problem. Derive the equation
d
d
x
e
i p·x
(−x
2
)
ν
=−iπ
2
Γ(2 −ν +ε)
Γ(ν)
−4π
2
µ
2
p
2
ε
−p
2
4
ν−2
. (1)
Solution. In three dimensions plane waves can be expanded into Bessel func-
tions and Legendre polynomials according to
e
i p·x
=e
i|p||x| cos θ
= ... . (2)
To prove (1) we need the generalization of this expansion to arbitrary di-
mensions. The exponential itself looks the same for any Euclidian dimension,
namely
e
i p·x
=e
i|p||x| cos θ
. (3)
Therefore the dimensionality enters only in the orthogonality property. The func-
tions of θ that we call C
i
(θ) shall be orthogonal with the weight (sin θ)
d−2
,
because the d-dimensional volume element is proportional to (sin ϑ)
d−2
(see

4.3 Dimensional Regularization 199
Exercise 4.5, (2)):
d
d
Ω C
i
(cos θ) C
j
(cos θ)
∼
π
0
dθ(sin θ)
d−2
C
i
(cos θ) C
j
(cos θ)
=
1
−1
dcosθ(sin
2
θ)
(d−3)/2
C
i
(cos θ) C
j
(cos θ)
=
1
−1
dx (1 −x
2
)
(d−3)/2
C
i
(x) C
j
(x). (4)
Orthogonal polynomials with the weight (1 −x
2
)
d−1/2
are the “Gegenbauer
polynomials” C
(α)
n
(x).
9
The important properties for us are
e
i px cos θ
=Γ(ν)
px
2
−ν
∞
k=0
(ν +k) i
k
J
ν+k
( px) C
(ν)
k
(cos θ) (5)
with arbitrary ν,
1
−1
dx (1 −x
2
)
α−1/2
C
(α)
n
(x)C
(α)
n
(x)
=δ
nn
π2
1−2α
Γ(n +2α)
n!(n +α) [Γ(α)]
2
α>−
1
2
, (6)
and
C
(α)
0
(x) = 1 . (7)
From (6) and (7) we find that
1
−1
dx (1 −x
2
)
α−1/2
C
(α)
n
(x) =
1
−1
dx (1 −x
2
)
α−1/2
C
(α)
n
(x)C
(α)
0
(x)
= δ
n0
π2
1−2α
Γ(2α)
α[Γ(α)]
2
= δ
n0
1
−1
dx (1 −x
2
)
α−1/2
. (8)
9
Their properties can be found, for example, in M. Abramowitz and A. Stegun: Hand-
book of Mathematical Functions, Chap. 22. (Dover, 1972).
Exercise 4.6

200 4. Gauge Theories and Quantum-Chromodynamics
Exercise 4.6
Comparing (8) with the d-dimensional integral (4) we find that α has to be chosen
as α =
d
2
−1. Using (6), relation (4) can now be denoted as
d
d
Ω C
d/2−1
i
(cos θ) C
d/2−1
j
(cos θ) = δ
ij
π2
3−d
Γ(i −2 +d)
i!
i −1 +
d
2
Γ
d
2
−1
2
,
or
d
d
Ω C
α
i
(cos θ) C
α
j
(cos θ) = δ
ij
π2
1−2α
Γ(i +2α)
i!(i +α) [Γ(α)]
2
,
α =
d
2
−1
, (9)
and, furthermore,
d
d
Ω =
1
−1
dx (1 −x
2
)
(d−3)/2
=
π2
3−d
Γ(d −2)
d
2
−1
Γ
d
2
−1
2
. (10)
The angular integral is now easy to perform. We first substitute x
0
→−ix
0
E
to
go to Euclidian coordinates. We also substitute p
0
→i p
0
E
. Note that always the
time components only are Wick-rotated!
d
d
x
e
i p·x
(−x
2
)
ν
=−i
d
d
x
E
e
i p
E
x
E
cos θ
(x
2
E
)
ν
=−i
∞
0
dx
E
x
d−1
E
(x
2
E
)
ν
Γ(α)
p
E
x
E
2
−α
×
∞
k=0
(α +k)i
k
J
α+k
( p
E
x
E
)
d
d
Ω C
(α)
k
(cos θ)
=−i
∞
0
dx
E
(x
E
)
d−1−2ν
Γ(α)
p
E
x
E
2
−α
αJ
α
( p
E
x
E
)
d
d
Ω
=−i
2π
d/2
Γ(d/2)
Γ(d/2−1)
p
E
2
1−d/2
d
2
−1
×
∞
0
dx
E
(x
E
)
d−1−2ν−d/2+1
J
d/2−1
( p
E
x
E
)
=−i2π
d/2
p
E
2
1−d/2
∞
0
dx
E
x
d/2−2ν
E
J
d/2−1
( p
E
x
E
)
=−i2π
d/2
p
E
2
1−d/2
( p
E
)
−1−d/2+2ν
∞
0
dyy
d/2−2ν
J
d/2−1
(y). (11)
4.3 Dimensional Regularization 201
The remaining integral can be found in appropriate integral tables.
10
∞
0
dyy
d/2−2ν
J
d/2−1
(y) = 2
d/2−2ν
Γ
d
4
+
d
4
−ν
Γ
d
4
−
d
4
+ν
. (12)
Putting all this together we get
d
d
x
e
i p·x
(−x
2
)
ν
=−iπ
d/2
( p
E
)
2ν−d
2
d/2
2
d/2−2ν
Γ(d/2−ν)
Γ(ν)
. (13)
Finally we insert again d = 4 +2ε to obtain the result
d
d
x
e
i p·x
(−x
2
)
ν
=−iπ
2
p
2
E
4
ν−2
4π
p
2
E
ε
Γ(2 −ν +ε)
Γ(ν)
, (14)
which completes our proof. Note that p
2
E
=−p
2
!
EXERCISE
4.7 Feynman Parametrization
Problem. Prove the most general form of the Feynman parametrization,
n
;
i=1
1
a
A
i
i
=
Γ(A)
<
n
i=1
Γ(A
i
)
1
0
<
n
i=1
dx
i
x
A
i
−1
i
n
i=1
a
i
x
i
A
δ
1 −
n
i=1
x
i
, (1)
with A =
n
i=1
A
i
by means of mathematical induction. The a
i
(i = 1, 2, ..., n)
are arbitrary complex numbers.
Solution. To prove (1) we start with the simple formula
1
a ·b
=
1
0
dx
(
ax −b(1 −x)
)
2
, (2)
which is obtained by observing that
1
a ·b
=
1
b −a
1
a
−
1
b
=
1
b −a
b
a
dz
z
2
. (3)
10
See, for example, I. Gradshtein and I. Ryshik: Tables of Series, Products and Inte-
grals, No. 6.151.14 (Harri Deutsch, Frankfurt am Main 1981).
Exercise 4.6

202 4. Gauge Theories and Quantum-Chromodynamics
Exercise 4.7
Substituting z = ax +b(1 −x) one obtains (2). Equation (2) can be further
generalized to arbitrary powers by taking derivatives
∂
A
∂a
A
∂
B
∂b
B
(4)
on both sides so that
1
a
A
·b
B
=
Γ(A +B)
Γ(A)Γ(B)
1
0
dx
x
A−1
(a −x)
B −1
(
ax +b(1 −x)
)
A+B
=
Γ(A +B)
Γ(A)Γ(B)
1
0
dx dy
x
A−1
y
B −1
(
ax +by
)
A+B
δ(1 −x −y). (5)
Thus we have proven (1) for n = 2. Now we assume that the formula (1) holds
for n and prove that it is also valid for n +1. Let us start with the expression
1
a
A
n+1
n+1
n
;
i=1
1
a
A
i
i
=
Γ(A)
<
n
i=1
Γ(A
i
)
1
0
<
n
i=1
dx
i
x
A
i
−1
i
n
i=1
a
i
x
i
A
δ
1 −
n
i=1
x
i
1
a
A
n+1
n+1
,
(6)
where we multiplied (1) on both sides by 1/a
A
n+1
n+1
. Applying (5) we can rewrite
(6) to obtain
n
;
i=1
1
a
A
i
i
=
Γ(A)
<
n
i=1
Γ(A
i
)
1
0
n
;
i=1
dx
i
x
A
i
−1
i
δ
1 −
n
i=1
x
i
Γ(A + A
n+1
)
Γ(A)Γ(A
n+1
)
×
1
0
dx
n+1
dy
y
A−1
x
A
n+1
−1
n+1
y
n
i=1
a
i
x
i
+a
n+1
x
n+1
A+A
n+1
δ
(
1 − y −x
n+1
)
.
(7)
Now we change variables
˜
x
i
= yx
i
(i = 1, 2,...n) in the above equation and
perform the y integration. After replacing
˜
x
i
by x
i
we obtain
n+1
;
i=1
1
a
A
i
i
=
Γ(A + A
n+1
)
<
n+1
i=1
Γ(A
i
)
1
0
<
n+1
i=1
dx
i
x
A
i
−1
i
n+1
i=1
a
i
x
i
A+A
n+1
δ
1 −
n+1
i=1
x
i
. (8)
This completes the proof of (1).
4.4 The Renormalized Coupling Constant of QCD 203
4.4 The Renormalized Coupling Constant of QCD
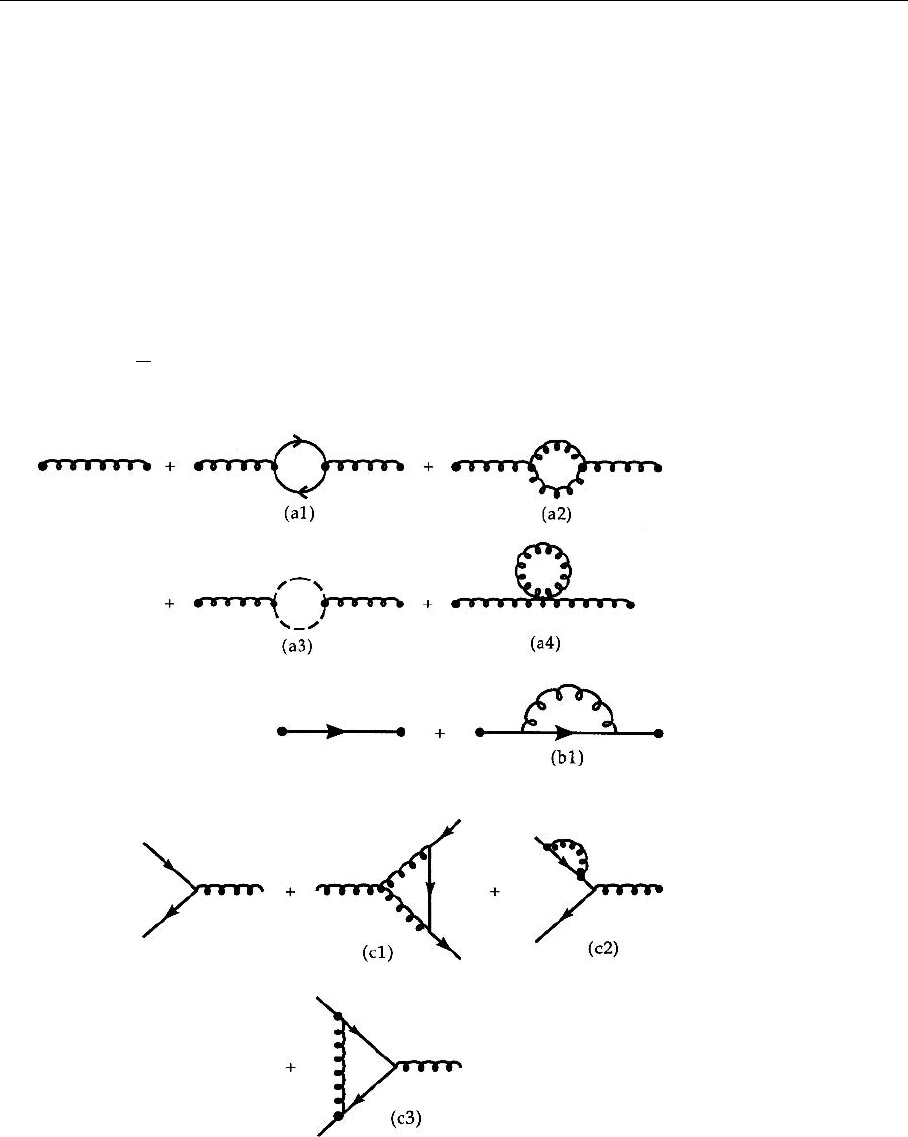
We shall now use dimensional regularization to calculate the renormalized QCD
coupling constant to lowest order. The divergent graphs contributing to the renor-
malization of g
s
belong to three classes, shown in Figs. 4.14, 4.15, and 4.16. Let
us work them out one by one.
Graph (a1). We start with vacuum polarization, in particular with the
fermion graph (a1) in Fig. 4.14. This graph is depicted in greater detail in
Fig. 4.17. One may wonder why the quantum numbers of the outgoing gluon
k
, a
,µ
are not identical with those of the ingoing gluon. Of course, this is the
most general case. It will turn out that indeed a = a
(see (4.119)) and k = k
(momentum conservation), but µ = µ
. Furthermore, in (4.133) and below, we
shall see that only the sum of all four vacuum polarization graphs (a1)–(a4) is
proportional to
1
k
2
(k
µ
k
µ
−g
µµ
k
2
), i.e. the projector which ensures gauge in-
Fig. 4.14. The vacuum po-
larization graphs of QCD
Fig. 4.15. The self energy
graphs of QCD
Fig. 4.16. The vertex cor-
rection graphs of QCD

204 4. Gauge Theories and Quantum-Chromodynamics
Fig. 4.17. The variables cho-
sen for the quark loop con-
tribution to vacuum polar-
ization
variance. Using the QCD Feynman rules it is easy to write down the polarization
tensor:
Π
aa (a1)
µµ
(k) =
N
F
i=1
g
2
d
4
q
(2π)
4
×tr
)
λ
a
2
λ
a
2
q/ +k/ +m
(q +k)
2
−m
2
+iη
γ
µ
q/ +m
q
2
−m
2
+iη
γ
µ
*
. (4.106)
N
F
is the number of quark flavors in the theory, or more precisely the number
of quarks with m
2
|k
2
|. The whole calculation can be carried through for ar-
bitrary m
2
, but one finds that the contribution is suppressed for m
2
> |k
2
|. N
F
therefore counts only the light flavors and for simplicity we can set m = 0inwhat
follows whenever this does not lead to infrared divergencies. The trace over the
color indices gives simply
tr
)
λ
a
2
λ
a
2
*
=δ
aa
1
2
. (4.107)
As usual we introduce Feynman parameters
1
(q +k)
2
−m
2
+iη
1
q
2
−m
2
+iη
=
1
0
dz
1
[q
2
+2kq z +(k
2
−m
2
)z −m
2
(1 −z) +iη]
2
=
1
0
dz
1
[(q +kz)
2
+k
2
z(1 −z) −m
2
+iη]
2
. (4.108)
To get rid of the linear term in the denominator we substitute q
µ
→q
µ
=q
µ
−k
µ
z:
Π
(a1)
µµ
(k) = g
2
N
F
2
1
0
dz
∞
0
d
4
q
(2π)
4
tr
$
[q/ +k/(1 −z)]γ
µ
[q/ −k/z]γ
µ
%
[q
2
+k
2
z(1 −z) −m
2
+iη]
2
, (4.109)
where we have dropped the color indices, i.e. Π
ab
µν
= δ
ab
Π
µν
. Here the term pro-
portional to m
2
in the nominator has already been dropped. Next we take the trace
and neglect all terms proportional to odd powers of q. They are zero as can be
seen by substituting q
ν
for −q
ν
. For the same reason in intergrations over even
powers of q only diagonal terms contribute:
d
4
qq
µ
q
ν
f(q
2
) = g
µν
× const =
1
4
d
4
qg
µν
q
2
f(q
2
). (4.110)

4.4 The Renormalized Coupling Constant of QCD 205
The left-hand side is a Lorentz tensor. After integrating over q the only possible
Lorentz tensor is g
µν
. By contracting both sides with g
µν
we see that the factor
1/4 is necessary to have the correct normalization (tr g = g
µ
µ
= 4). Therefore
(4.109) becomes
Π
(a1)
µµ
(k) = g
2
N
F
2
4
1
0
dz
×
∞
0
d
4
q
(2π)
4
2q
µ
q
µ
−q
2
g
µµ
−z(1−z)(2k
µ
k
µ
−k
2
g
µµ
)
[q
2
+k
2
z(1 −z) −m
2
+iη]
2
=2g
2
N
F
1
0
dz
×
∞
0
d
4
q
(2π)
4
−
1
2
q
2
g
µµ
−z(1−z)(2k
µ
k
µ
−k
2
g
µµ
)
[q
2
+k
2
z(1 −z) −m
2
+iη]
2
. (4.111)
Now only q
2
appears in the integrand, so it can safely be continued to Euclidian
space, q
µ
→
˜
q
µ
=(iq
0
, q), and translated into a d-dimensional integral:
Π
(a1)
µµ
(k) ⇒ 2g
2
N
F
1
0
dz
∞
0
i
d
d
˜
q
(2π)
4
µ
4−d
1
2
˜
q
2
g
µµ
−z(1 −z)(2k
µ
k
µ
−k
2
g
µµ
)
[
˜
q
2
−k
2
z(1 −z) +m
2
−iη]
2
.
(4.112)
We have introduced a dimensional quantity µ to keep the total dimension of the
expression unchanged. The integration is four-dimensional, i.e.
+
d
4
....Ifthis
is changed into
+
d
d
... with the same integrand, a factor µ
4−d
ensures the same
dimension of the whole expression. With (4.81) it follows that
Π
(a1)
µµ
(k) =
2ig
2
N
F
(2π)
4
1
0
dz
π
d
2
µ
4−d
Γ
d
2
m
2
−k
2
z(1 −z) −iη
d
2
−2
×
Γ
2 −
d
2
Γ
d
2
Γ(2)
[−z(1−z)]
2k
µ
k
µ
−k
2
g
µµ
+
2ig
2
N
F
(2π)
4
g
µµ
2
1
0
dz
π
d
2
µ
4−d
Γ
d
2
m
2
−k
2
z(1 −z) −iη
d
2
−1
×
Γ
1 −
d
2
Γ
1 +
d
2
Γ(2)
. (4.113)
206 4. Gauge Theories and Quantum-Chromodynamics
The terms on the right-hand side are divergent. For d = 4 −2ε the first is
proportional to
Γ
2 −
d
2
= Γ(ε) =
1
ε
+Γ
(1) +O(ε) , (4.114)
while the second term is proportional to
Γ
1 −
d
2
Γ
1 +
d
2
Γ
d
2
=
4 −2ε
2
Γ(−1 +ε)
= (2 −ε)
Γ(ε)
(−1+ε)
= (2 −ε)(−1 −ε)
1
ε
+Γ
(1)
+O(ε)
=−
2
ε
−1 −2Γ
(1) +O(ε) . (4.115)
We thus have
Π
(a1)
µµ
(k) =
2ig
2
N
F
(2π)
4
µ
4−d
π
d
2
1
ε
+Γ
(1)
×
1
0
dz
−z(1−z)
[m
2
−k
2
z(1 −z)]
ε
2k
µ
k
µ
−k
2
g
µµ
−
2ig
2
N
F
(2π)
4
µ
4−d
π
d
2
2
ε
+1 +2Γ
(1)
×
1
0
dz [m
2
−k
2
z(1 −z)]
1−ε
1
2
g
µµ
. (4.116)
It can now be seen that m
2
can safely be neglected. For this purpose the integrand
is expanded in m
2
/k
2
:
m
2
−k
2
z(1 −z)
−ε
= (−k
2
)
−ε
(z(1−z))
−ε
1 −
m
2
k
2
z(1 −z)
−ε
= (−k
2
)
−ε
(z(1−z))
−ε
×
1 +ε
m
2
k
2
1
z(1 −z)
+O
m
4
k
4
. (4.117)
The leading z integral can be performed easily,
1
0
dz
[
z(1 −z)
]
1−ε
=
Γ(2 −ε)Γ(2 −ε)
Γ(4 −ε)
=
1 −εΓ
(2)
2
3!−2εΓ
(4)
=
1
3!
−
ε
3
Γ
(2) +
ε
3
Γ
(4), (4.118)
4.4 The Renormalized Coupling Constant of QCD 207
and turns out to be finite for ε → 0. Thus, indeed, we can safely neglect the quark
mass since our expression is infrared safe. We get
Π
(a1)
µµ
(k) =
2ig
2
N
F
16π
2
π
ε
µ
2ε
−2k
µ
k
µ
+2k
2
g
µµ
−k
2
−ε
1
3!
1
ε
+const
=ig
2
N
F
16π
2
2
3
πµ
2
−k
2
ε
1
ε
+const
g
µµ
k
2
−k
µ
k
µ
+... .
(4.119)
Finally, we expand y
ε
=1 +ε ln(y):
Π
(a1)
µµ
(k) = g
2
i
N
F
16π
2
2
3
1
ε
+ln
πµ
2
−k
2
+const
g
µµ
k
2
−k
µ
k
µ
.
(4.120)
Note that every 1/ε term is always accompanied by a term ln(−k
2
/µ
2
).
With ln(−k
2
/πµ
2
) = ln(−k
2
/µ
2
) −ln(π) we can finally write
Π
(a1)
µµ
(k) = g
2
i
N
F
16π
2
2
3
1
ε
−ln
−k
2
µ
2
+const
g
µµ
k
2
−k
µ
k
µ
.
(4.121)
This completes the calculation of the quark loop graph of Fig. 4.17.
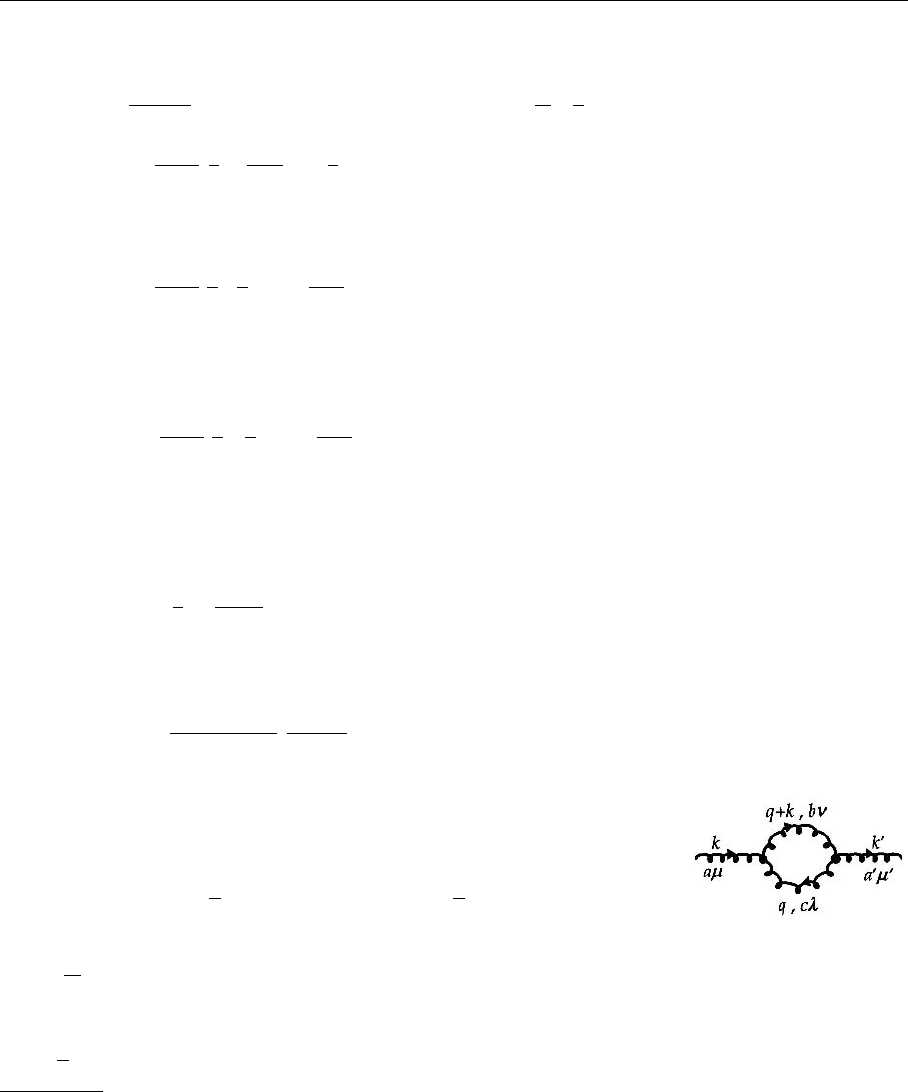
Graph (a2). Next we calculate the gluon loop with two 3-gluon vertices,
applying (19) of Example 4.2 twice:
Π
aa (a2)
µµ
(k) = g
2
1
2
d
4
k
(2π)
4
f
abc
[g
µλ
(k −q)
ν
+g
νµ
(−q −2k)
λ
+g
λν
(q +q +k)
µ
]
× f
a
bc
g
µ
λ
(−k +q)
ν
+g
ν
µ
(q +2k)
λ
+g
νλ
(−2q −k)
µ
×
1
(q +k)
2
+iη
1
q
2
+iη
. (4.122)
The factor 1/2 in front follows from combinatorics. Such combinatoric factors
are fairly easy to derive, as we shall now demonstrate for all the graphs relevant
for our calculation.
Let us start with the gluon loop. The 3-gluon vertex contains 6 terms, cor-
responding to the 3! orientations of the 3-gluon vertex. The total symmetry
factor is therefore (3!)
2
·
1
2!
(see Fig. 4.19). The factor
1
2!
stems from the general
pertubation theory series, which reads
∞
n=0
1
n!
(−i)
n
d
4
x
1
···d
4
x
n
T
ˆ
H
i
(t
1
)
ˆ
H
i
(t
2
) ···
ˆ
H
i
(t
n
)
,
where
ˆ
H
i
is the interaction Hamilton density. The second-order term acquires the
factor
1
2!
. For more details see W. Greiner and J. Reinhardt.
11
11
W. Greiner and J. Reinhardt: Field Quantization (Springer, Berlin, Heidelberg, New
York 1995).
Fig. 4.18. The chosen varia-
bles from the first gluon loop
contribution to vacuum po-
larization. For the distinc-
tion of the quantum num-
bers k
, a
,µ
of the outgo-
ing gluon from those of the
incoming gluon, see discus-
sion at the beginning of this
paragraph
