Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

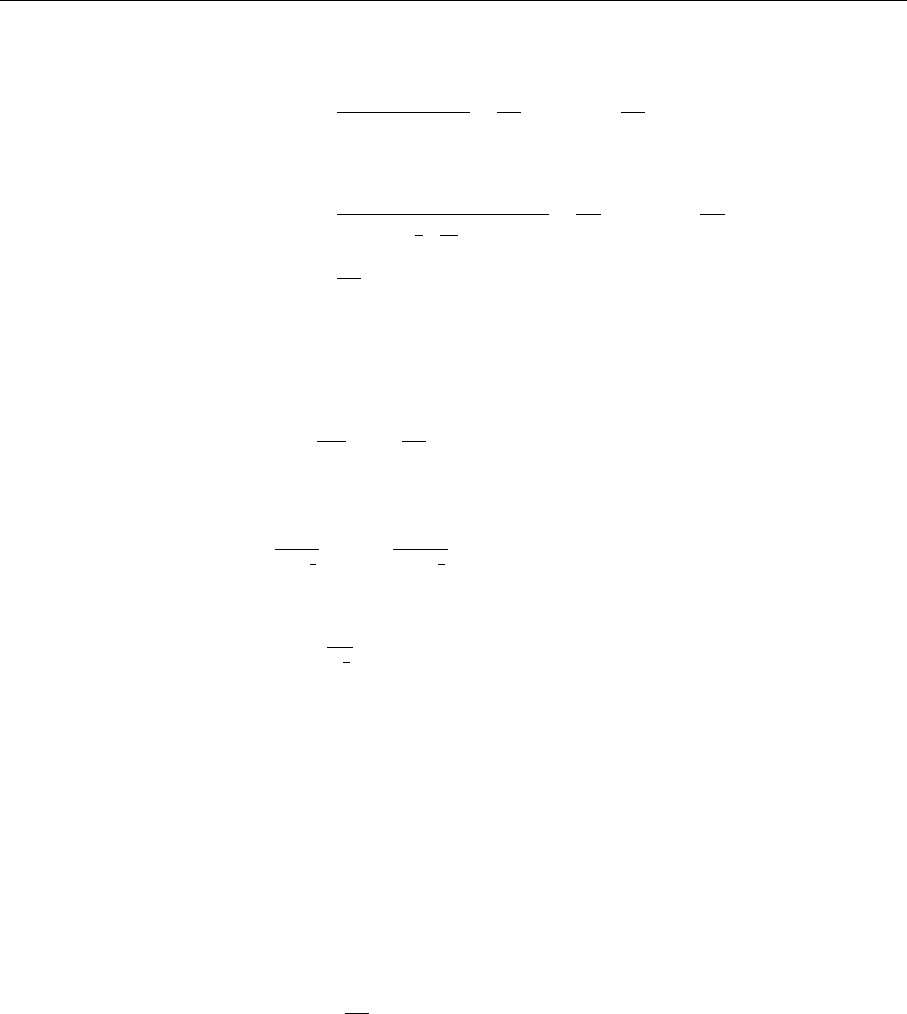
228 4. Gauge Theories and Quantum-Chromodynamics

where we have used (4.187) and (4.188). The total energy of the sea is then

sea

≡ E

−iε A

1 −cos(2πε/L)



2π

+i A

sin



2π



. (4.195)

Expanding in ε we get

sea

(1 −iε A

+ε

+...)

1 −1 +



2π



+...



2π

+i A

sin



2π



+...



2π

+O(ε) +a constant independent of A

. (4.196)

One remark is in order here. From the very beginning we assumed that the dy-

namics of A

is negligible when compared to the dynamics of the fermions. Let

us verify that this is indeed justiﬁed.

The effective Lagrange density determinig the quantum mechanics of A

L =

−

2π

. (4.197)

This is the ordinary harmonic oscillator with the wave function

exp



−



(4.198)

of the ground state and the level splitting

. (4.199)

The characteristic frequencies in the fermion sector are ω

∼ L

−1

. Hence,

/ω

∼ Le

1.

4.5.4 Standard Derivation

It will be extremely useful to discuss the connection between the picture pre-

sented above and the more standard derivation of the chiral anomaly in the

Schwinger model. The following discussion will serve as a bridge between the

physical picture described above and the standard approach to anomalies in QCD

and other gauge theories.

We would like to demonstrate that

∂ · J

2π

µν

, (4.200)

by considering directly the the divergence of the axial current. Then we need to

bother only about the ultraviolet regularization. In particular, the theory can be

considered in the inﬁnite space since the ﬁniteness of L does not affect the result

stemming from the short distances.

4.5 Extended Example: Anomalies in Gauge Theories 229

One of the convenient methods of the ultrviolet regularization is due to Pauli

and Villars. In the model at hand it reduces to the following: In addition to the

original massless fermions in the Lagrange density, heavy regulator fermions

are introduced with mass M

whereas the limit M

−→ ∞ is implied. Further-

more, each loop of the regulator fermions is supplied by an extra minus sign

relatively to the normal fermion loop. The role of the regulator fermions in

the low-energy regime (E  M

) is the introduction of an ultraviolett cut-off

in the formally divergent integrals corresponding to the fermion loops. Such

a regularization procedure automatically guarantees the gauge invariance and the

electromagnetic current conservation.

In the model regularized according to Pauli and Villars the axial current has

the form

5 µ

Ψγ

Ψ +

R γ

R , (4.201)

where R is the regulator fermion. In calculating the divergence of the regularized

current the naive equations of motions can be used. Then,

∂ · J



←

∂

·γγ

→

∂

·γγ



Ψ +



←

∂

·γγ

→

∂

·γγ





igγ · A

+igγ

γ · A





igγ · A

+igγ

γ · A

+2iM



=2iM

R γ

R . (4.202)

The divergence is non-vanishing, i.e. the axial current is not conserved! But, as

was expected, ∂

5 µ

contains only the regulator anomalous term.

The next step is to contract the regulator ﬁelds and calculate the relevant dia-

grams. In this context we may learn a new technique, the so-called background

ﬁeld technique which we shall use here in order to calculate the right hand side

of (4.202). One can write in momentum representation

2iM

R γ

R =−2M

γ ·P −M

≡−2M

(2π)

L+C



γ ·P −M



, (4.203)

where P = iD and tr

L+C

means the trace with respect to spin (Lorentz) and

colour indices; |p denotes a state vector describing a fermion with momen-

tum p. Note, that we have taken into account the fact that the minus sign in the

fermion loop does not appear for the regulator fermions.

Moreover,

γ ·P −M

γ ·P +M

γ ·P γ ·P −M

γ ·P +M

µν

−M

. (4.204)

230 4. Gauge Theories and Quantum-Chromodynamics

The second equality here stems from the deﬁnition of the gamma matrices and

the following property



, P



=−



, D



=i F

µν

. (4.205)

In fact, using (4.162) and (4.164) one may verify

γ ·P γ ·P =γ





, P



+2g

µν



iγ

µν

= P

µν

. (4.206)

Now, since M

−→ ∞ the trace in (4.203) can be expanded in inverse powers of

. In this way we get

γ ·P −M

=tr

(

γ ·P +M

)

(4.207)



−M

(−)

µν

−M

+...

(

The ﬁrst term in the expansion vanishes after taking the trace of the gamma ma-

trices. The third and all other terms are irrelevant because they vanish in the limit

−→ ∞. The only relevant term is the second one, where we can substitue

the operator P = iD = i∂ − A by the momentum p since the result is explicitly

proportional to the back ground ﬁeld. Then

2iM

Rγ

R =−2iM

(2π)



−M



µν

. (4.208)

The integration over p can be done with the help of the Feynman integral

≡

(2π)

( p

−M

)

(−π)

(2π)



α −



(−M

)

α−

. (4.209)

Thus,

2iM

Rγ

R =

2π

µν

. (4.210)

This computation completes the standard derivation of the anomaly. One should

have a very rich imagination to be able to see in these manipulaions the simple

physical nature of the phenomenon which has been described above (restruc-

turing of the Dirac sea and level crossing). Nevertheless, this is the same

phenomenon viewed from a different perspective – less transparent but more

economic since we get the ﬁnal result very quickly using the well-developed

machinery of the diagram technique.

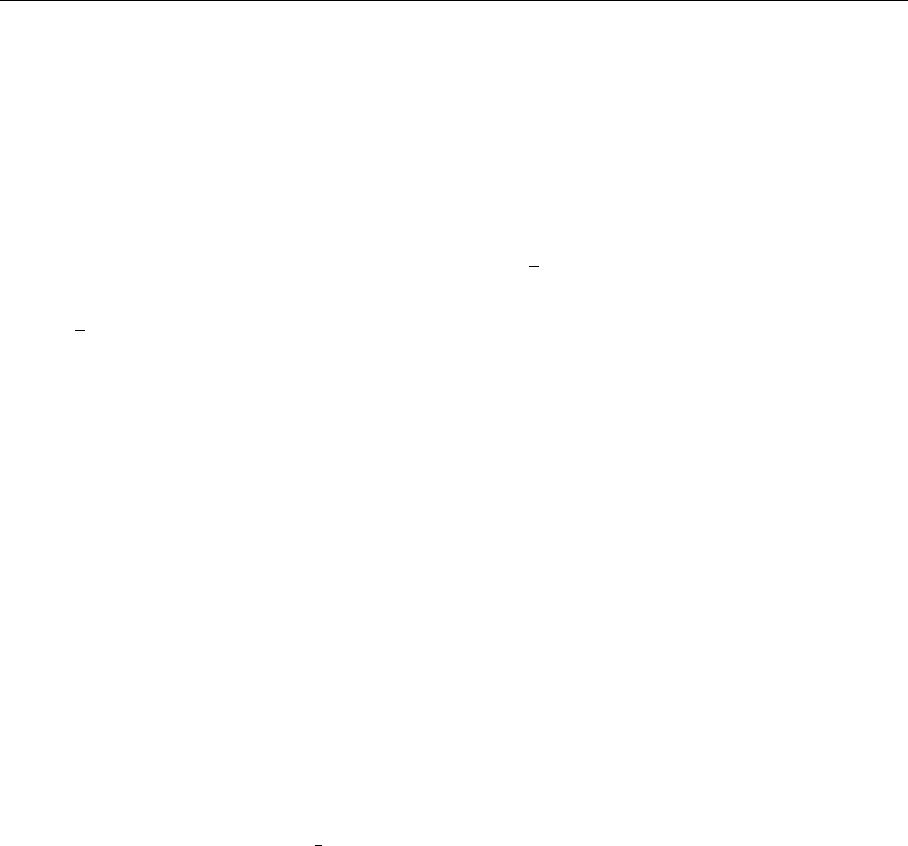
4.5 Extended Example: Anomalies in Gauge Theories 231

4.5.5 Anomalies in QCD

Before proceeding to quantum anomalies in QCD let us ﬁrst list the symme-

tries of the classical action. We will assume that the theory contains n

massless

quarks and for the moment forget the heavy quarks which are inessential in the

given context. The correction due to small u-, d-, and s-quark masses can be

considered seperately if necessary.

In the chiral limit, i.e. m

=0, the classical Lagrange density is

L =





Lα

i(γ)

αβ

·(D)

Lβ

Rα

i(γ)

αβ

·(D)

Rβ



−

µν

L,R

(1 ±γ

) q , (4.211)

where q is the quark ﬁeld and G is the gluon ﬁeld strength tensor. The action of

the classical theory is invariant under the following global transformations:

(1) Rotation of fermions of different ﬂavours,



q −→ U



q , (4.212)

where



q denote the n

-tupel of quark ﬂavours and U is a three-dimensional

unitary representation of an arbitrary element of the SU(3) group. Since the left-

handed and right-handed quarks enter in the Lagrange density as separate terms,

the Lagrange density actually possesses SU(3)

×SU(3)

symmetry, called the

chiral ﬂavour invariance.

(2) The U(1) transformations,

vector: q

L,R

−→ exp

(

+iα

)

L,R

(4.213)

axial: q

−→ exp

(

+iβ

)

, q

−→ exp

(

−iβ

)

. (4.214)

The physical meaning of this transformations is, that in the classical theory the

charge of the left-handed and right-handed fermions are conserved seperately.

(3) The scale transformations

A(x) −→ λ A(λx), q(x) −→ λ

q(λx). (4.215)

The scale invariance stems from the fact that the classical action contains no

dimensional constants.

At the quantum level the fate of the above symmetries is different. The cur-

rents generating the chiral ﬂavour tranformations are conserved even with the

ultraviolet regularization switched on. They are anomaly-free in pure QCD. The

vector U(1) invariance also stays a valid anomaly-free symmetry at the quantum

level. This symmetry is responsible for the fact that the quark number is constant

in any QCD process. Finally, the current generating the axial U(1) transform-

ations and the dilatation current are not conserved at the quantum level due to

anomalies, as we will show below.

232 4. Gauge Theories and Quantum-Chromodynamics

4.5.6 The Axial and Scale Anomalies

As explained above, the concrete form of the anomalous relations can be es-

tablished without going beyond perturbation theory, provided an appropriate

ultraviolet regularization is chosen. It is important to note that in the litera-

ture two languages are used for the description of one and the same anomalous

relations and many authors do even not realize the distinction between the

languages.

Within the ﬁrst approach one establishes an operator relation, say, between

the divergence of the axial current and G

µν

(see below). Both, the axial cur-

rent and G

µν

are treated within this procedure as Heisenberg operators of the

quantum ﬁeld theory. In order to convert the operator relations into amplitudes it

is necessary to make one more step: to calculate according to the general rules the

matrix elements of the operators occuring in the right-hand and left-hand sides

of the anomalous equality.

Within the second approach one analyzes directly the matrix elements. More

exactly, one ﬁxes usually an external gluonic ﬁeld and determines the divergence

of the axial current in this ﬁeld. In the absence of the external ﬁeld the axial cur-

rent is conserved. The existence of the anomaly implies that the axial current is

not conserved and that the divergence of the axial current is locally expressible in

terms of the external ﬁeld. The analysis of the anomaly in the Schwinger model

has been carried out just in this way.

Although one and the same letters are used in both cases – perhaps, the con-

fusion is due to this custom – it is quite evident that the Heisenberg operator at

the point x and the expression for the background ﬁeld at the same point are by

no means identical objects. Certainly, in the leading order

µν





µν



ext

µν





µν



ext

, (4.216)

where ... denotes in the case at hand averaging over the external gluon ﬁeld

while the subscript “ext” marks the external ﬁeld. In the next-to-leading order,

however, the right-hand side of equation (4.216) acquires an α

correction.

Therefore if the anomalies are discussed beyond the leading order it is absolutely

necessary to specify what particular relations are considered: the operator rela-

tions or those of the matrix elements. Only in the one-loop approximation do

both versions superﬁcially coincide. In the remainder of this chapter the term

“anomaly” will mean the operator anomalous relation.

Let us begin with the axial anomaly since it is simpler in the technical sense

and a close example has been analyzed already in the Schwinger model.

The current generating the axial U(1) transformation is



q γ

q . (4.217)

Differentiating and invoking the equation of motion γ · Dq = 0weget

∂ · J





←

·γγ

q −

q γ

γ ·

→



=0 . (4.218)

4.5 Extended Example: Anomalies in Gauge Theories 233

The lesson obtained in the Schwinger model teaches us, however, that this is not

the whole story and the conservation of the axial current will be destroyed after

switching on the ultraviolet regluarization. In the Schwinger model on the cir-

cle we deal with the weak coupling regime and, therfore, can choose any of the

alternative lines of reasoning either based on the infrared or on the ultraviolet ap-

proaches. In QCD it is rather meaningless to speak about the infrared behaviour

of quarks. To make the calculation of the anomaly reliable we must invoke only

the Green functions at short distances.

We use the ε-splitting for the ultraviolet regularization and write again

reg

5 µ



q(x +ε) γ

exp

⎛

⎝

x+ε

x−ε

dy· A(y)

⎞

⎠

q(x −") . (4.219)

In what follows it is convenient (of course not obligatory) to impose the so called

Fock–Schwinger gauge

(x −x

) · A

(x) = 0 (4.220)

where x

is an arbitrary point in space-time playing the role of a gauge parameter.

Let us notice that the condition (4.220) is invariant under scale transformations

and inversion of the coordinates, but breaks the translational symmetry. The lat-

ter restores itself in gauge invariant quantitities. In other words, the parameter x

should cancel out in all correlation functions induced by colourless sources. This

fact may in principal serve as an additional check of correctness of the actual cal-

culation. Nevertheless, we shall not exploit this useful property and put x

= 0

in all following considerations,

x · A

(x) = 0 (4.221)

getting compact formulae for the quark propagator in the background ﬁeld. The

most important consequence of (4.221) is that the potential is directly express-

able in terms of the gluon ﬁeld strength tensor. Let us derive this result in detail.

We start with the identity

(x) ≡ ∂



x · A

(x)



−x

∂

(x), (4.222)

where due to (4.221) the ﬁrst summand on the right-hand side vanishes. The

second term can be rewritten as follows

a µν

(x) −x ·∂ A

(x). (4.223)

Combining the equations (4.222) and (4.223) we get

(

1 +x ·∂

)

(x) = x

a νµ

(x). (4.224)

With the substitution x = αy one immediately sees that the left-hand side of

(4.224) reduces to a full derivative

dα



αA

(αy)



= αy

νµ

(αy). (4.225)

234 4. Gauge Theories and Quantum-Chromodynamics

Integrating over α from 0 to 1 we arrive at

(x) =

dααx

νµ

(αx), (4.226)

which is the desired expression.

For our purpose it is much more convenient to deal with another represen-

tation of the potential because we are interested here in the expansion in local

operators O(), i.e. the gluon ﬁeld strength tensor and its covariant derivatives

at the origin. This is achieved by a Taylor expansion of the gluon ﬁeld strength

tensor in (4.226):

(x) =

2 ·0!

νµ

(0) +... , (4.227)

where the dots denote terms with derivatives of the gluon ﬁeld strength tensor.

Now let us return to the ultraviolet regularized version of the axial current

(4.219) and calculate its divergence

∂ · J

reg



q(x +ε)

←

∂

·γγ

exp

⎛

⎝

x+ε

x−ε

dy · A(y)

⎞

⎠

q(x −ε)



q(x +ε) exp

⎛

⎝

x+ε

x−ε

dy · A(y)

⎞

⎠

γ ·

→

∂

q(x −ε)

−



q(x +ε) γ

γ ·∂ exp

⎛

⎝

x+ε

x−ε

dy · A(y)

⎞

⎠

q(x −ε) . (4.228)

Using the equations of motions for quarks in the ﬁrst and second line of (4.228)

and differentiating the exponential we get

∂ · J

reg



q(x +ε) (−ig)γ· A(x +ε)γ

exp

⎛

⎝

x+ε

x−ε

dy · A(y)

⎞

⎠

q(x −ε)



q(x +ε) exp

⎛

⎝

x+ε

x−ε

dy · A(y)

⎞

⎠

(−)γ

igγ · A(x −ε) q(x −ε)

−



q(x +ε) γ

igγ ·

(

A(x +ε) − A(x −ε)

)

×exp

⎛

⎝

x+ε

x−ε

dy · A(y)

⎞

⎠

q(x −ε) . (4.229)

4.5 Extended Example: Anomalies in Gauge Theories 235

Let us impose the Fock–Schwinger gauge condition and use the expansion

(4.227) of the vector potential in (4.229). Expanding the exponential up to order

we obtain

∂ · J

reg

=−2ig



q(x +ε) ε

νµ

(0)γ

q(x −ε) . (4.230)

Contracting the quark lines in the loop we arrive at the following expression we

arrive at the following expression

∂ · J

reg

L+C



−2ig ε

νµ

(0)γ

(−i)S(x −ε, x +ε)



, (4.231)

where S(x, y) is the massless quark propagator in the background ﬁeld. The

expression for this propagator as a series in the background ﬁeld in the Fock–

Schwinger gauge is

S(x, y) = S

(0)

(x −y) +S

(1)

(x, y) +S

(2)

(x, y) +... , (4.232)

whereby

(0)

(x −y) =

2π

(−r

)

(4.233)

with r = x −y and the corrections to free propagation up to Order O(g

) are

(1)

(x, y) =

4π

(−r

)

νµ

(0) +

8π

−r

λ



(4.234)

(2)

(x, y) =−

192π

(−r

)



−(xy)



(0). (4.235)

Notice that under the standard choice of the origin, y =0, the ﬁrst term in

(1)

and the whole second order contribution S

(2)

vanishes. Inserting (4.232) in

(4.231) and neglecting all term vanisihing in the limit ε → 0weﬁnd

∂ · J

reg

=−n

νµ

a αβ

(0)

8π





4π

µν

(0), (4.236)

a µν

µνσ

σ

. (4.237)

Notice that quarks propagate only very short distances ε −→ 0. The expression

(4.236) gives the axial anomaly in the one-loop approximation,

∂ · J

4π

µν

. (4.238)

V.A. Novikov, M.A. Shifman, A.I. Vainshtein and V.I. Zakharov, Fortsch. Phys. 32,

585 (1985).

236 4. Gauge Theories and Quantum-Chromodynamics

This result is readily reproducible within the Pauli–Villars regularization. Higher

order modiﬁcations will be discussed below.

Let us proceed now with the scale anomaly. First of all it is instructive to

check that the scale transformations are generated by the current

d ν

= x

µν

, (4.239)

where T

µν

are the components of the energy-momentum tensor (symmetric and

conserved),

µν

=−G

µ



ν a

µν

σ





←→

+γ

←→



q . (4.240)

The corresponding charge can be represented as

≡

d 0

= tH+

, k ∈{1, 2, 3} , (4.241)

where H is the Hamiltonian. For

the following algebraic relations hold



, p



=i p



, exp





=−





exp





. (4.242)

Let O(x) be an arbitrary colourless operator. Then

[

, O(x)

]

[

H, O(x)

]



, O(x)



=−i

∂

∂t

O(x) +



, O(x)



. (4.243)

Moreover, the commutator



, O(x)



contains two terms, the ﬁrst term corres-

ponds to a rescaling of the space coordinate and the second one to a rescaling of

the operator O. Indeed,



, O(x)





, exp





O(t, 0)exp



−ix



(4.244)



, exp





O(t, 0)exp



−ix



+exp





O(t, 0)



, exp



−ix



+exp







, O(t, 0)



exp



−ix



=−ix

∂

O(t, x) +exp







, O(t, 0)



exp



−ix



4.5 Extended Example: Anomalies in Gauge Theories 237

The commutator



, O(t, 0)



should be proportional to O(t, 0), hence

[

D, O(x)

]

=−i

(

x ·∂ +d

)

O(x), (4.245)

where d is a dimensionless number determined by the particular form of the

operator O.

Only the general properties of quantum ﬁeld theories have been used so far.

The numerical value of the coefﬁcient d depends on the speciﬁc structure of the

underlying theory. In QCD d is equal to the normal dimension of the operator O,

for nstance, if O = L where L is the Lagrange density of QCD, then d = 4.

Equation (4.245) expresses in a mathematical language the change of the units

of length and mass. This explains the origin of the name “scale transformations”.

Notice that the restriction on colourless operators is not superﬂuous. For any

coloured operator the commutator with Q

, as seen by direct calculation, does

not reduce to the form (4.245). One should not be puzzled by this fact. The

complication which arise are due to gauge ﬁxing, i.e. additional terms can be

eliminated by an appropriate gauge transformation.

Using the classical equations of motions we get

∂ · J

= T

=0 . (4.246)

In the classical theory the trace of the energy-momentum tensor vanishes pro-

vided that no explicit mass term occurs in the Lagrange density. At the quatum

level the energy-momentum tensor is no longer traceless and its trace is given by

the scale or dilatation anomaly. The fact that the scale invariance (4.215) is lost

in loops is obious. Indeed, the invariance (4.215) takes place because there are

no parameters with mass dimension in the classical action. Already at the one-

loop level, however, such a parameter inevitably appears in the effective action,

the ultraviolet cut-off M

The M

dependence of the effective action is known beforhand. It is very

convenient to use this information, seemingly it is the shortest way to calcu-

late the trace of the energy-momentum tensor. In the one-loop approximation the

effective action can be written somewhat symbolically as

eff

=−



−

16π

lnM

char





µν



ext

+... , (4.247)

where b =

−

is the ﬁrst coefﬁcient in the Gell-Mann–Low function,

char

denotes the characteristic length scale and the dots stand for the fermion

terms. We rescaled the gluon ﬁeld, gA −→ A, so that the coupling constant ﬁg-

ures only as an overall factor in front of G

. The variation of the effective action

under the transformation (4.215) is

δS

eff

=−

32π

ln(λ) , (4.248)

implying that

∂ · J

=−

32π

. (4.249)