Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

218 4. Gauge Theories and Quantum-Chromodynamics

and therefore

)

−

(−k

)

=−b



−k



. (4.148)

Solving for g

(−k

) = 4πα

(−k

) yields

(−k

) =

)

1 +

4π



11 −





−k



, (4.149)

which is the running coupling constant up to one-loop order (note that C

= 3in

QCD).

It is instructive to compare our results (4.142) with those obtained for

a different gauge, namely the Landau gauge, in which the gluon propagator is

−g

µν

+iη

. (4.150)

In this gauge, instead of (4.133) one obtains

)

µµ



+Π

)

µµ



Landau

= i

3δ



16π



−ln



−k



+...





−g

µµ



), (4.151)

instead of (4.136)

(k) = 0 , (4.152)

and instead of (4.141)

a (c)

16π



−ln



−k



+...



. (4.153)

Together this gives

= g

−

16π



−



−ln



−k



+...



= g

−

16π



−



−ln



−k



+...



. (4.154)

Thus the β function as an observable is gauge independent, as it must be, but

the renormalization of the wave function owing to the self-energy graph and the

vacuum polarization graphs is gauge dependent. For completeness let us also cite

4.4 The Renormalized Coupling Constant of QCD 219

the result for the β function to third order:

β(g) =−

(4π)



−



−

(4π)



−2C

−



−

(4π)



2857

−

205

−

1415



(4.155)

with C

= N (see (4.124)) for SU(N ) and C

=tr

/N = 4/3 for quarks in

the fundamental representation.

For QCD this simpliﬁes to

β(g) =−

(4π)



11 −



−

(4π)



102 −



−

(4π)



2857

−

5033

325



. (4.156)

Up to second order this can be translated into an explicit solution for α

= g

/4π

(µ) =

12π

(33 −2N

) ln





⎡

⎣

1 −

6(153 −19N

)

(33 −2N

)











⎤

⎦

(4.157)

where we have introduced the famous Λ

QCD

parameter (see Example 4.3). It is

explained there that Λ

QCD

=Λ

QCD





, i.e., it is a function of the renormaliza-

tion scale M

. To third order, such an explicit expansion cannot be given. This is

because one actually expands simultaneously in ln µ

/Λ

and ln





/Λ



Such a double expansion becomes ambiguous at higher orders.

Let us ﬁnally note that the higher terms of the β function, i.e., the cofﬁcient of

and g

depend on the regularization scheme used, leading to different Λ

QCD

parameters for different renormalization schemes, which are correlated with dif-

ferent expressions in the large bracket on the right-hand side of (4.157). This will

be explicitly discussed for the lattice gauge regularization in Sect. 7.1.

See O.V. Tarasov, A.A. Vladimirov, and A.Yu. Zharkov: Phys. Lett. B 93, 429 (1980);

S.A. Larin and J.A.M. Vermaseren: Phys. Lett. B 303, 334 (1993).

220 4. Gauge Theories and Quantum-Chromodynamics

4.5 Extended Example: Anomalies in Gauge Theories

In this extended example we will discuss the origin of quantum anomalies. Let us

ﬁrst explain what the term quantum anomalies in ﬁeld theory means. Consider

the action of a classical ﬁeld theory which is invariant under certain symmetry

transformations. If this invariance cannot be preserved at the quantum level, i.e.,

when quantum corrections are taken into account, such a phenomenon is called

a quantum anomaly.

We will concentrate on the physical meaning of the phenomenon and demon-

strate the existence of two important anomalies in ﬁeld theories: the chiral and

the scale anomaly.

4.5.1 The Schwinger Model on the Circle

Before discussing the scale anomaly in QCD and its connection to the QCD

β function we analyse the chiral anomaly in one of the simplest gauge ﬁeld

models, namely the Schwinger model on a circle. The Schwinger model is two-

dimensional QED with massless Dirac fermions. The Langrange density for this

model is

L =−

Ψ iγ · DΨ, (4.158)

where e

is the bare gauge coupling constant having mass dimension D = 2, F is

the gauge ﬁeld strength tensor with components

µν

= ∂

−∂

, (4.159)

D denotes the covariant derivative with components

=∂

+ie

(4.160)

and Ψ is the two-component spinor ﬁeld. The gamma matrices can be chosen as

Pauli matrices in the following way:

= σ



0 −i



,γ

=iσ





,γ

=σ



0 −1



(4.161)

Note that γ

=γ

. The Pauli matrices are in fact two dimensional represen-

tations of the gamma matrices since

+γ

=2 g

µν

with g

µν

=γ

5 µν

. (4.162)

With the two dimensional antisymmetric tensor

" =



−10



(4.163)

4.5 Extended Example: Anomalies in Gauge Theories 221

one also veriﬁes explicitely the relations

µν

, (4.164)

which will be useful later on.

The spinor Ψ

≡(ψ

, 0) will be called left-handed (γ

=+Ψ

), while the

spinor Ψ

≡(0,ψ

) with γ

=−Ψ

will be called right-handed.

In spite of the considerable simpliﬁcations compared to the four-dimensional

QED, the dynamics of the model (4.158) is still too complicated for our purpose.

In order to simplify the situation further let us consider the system described by

(4.158) in a ﬁnite spatial domain of length L. We impose periodic boundary con-

ditions on the gauge ﬁeld and (just for convenience) antiperiodic ones for the

massless Dirac fermions. Thus



t, −



= A



t, +



,Ψ



t, −



=−Ψ



t, +



(4.165)

These conditions impose that the gauge ﬁeld A and the Dirac fermions Ψ

can be expanded in Fourier modes, i.e exp(ikx 2π/L) for the bosons and

exp[i(k +1/2)x 2π/L) for the fermions.

Now let us recall that the Lagrange density (4.158) is invariant under the local

gauge transformations

Ψ −→ e

iα(t,x )

Ψ, A

−→ A

−∂

α(t, x). (4.166)

It is quite evident that all modes for the ﬁeld A

except for the zero mode can be

gauged away. Indeed, terms of the type a(t)exp(ikx 2π/L) in A

with nonzero

momentum can be gauged away with α(t, x) =−(ik)

−1

a(t)exp(ikx 2π/L).This

choice for the gauge function is in agreement with the boundary conditions

(4.165), i.e. the gauge function is periodic on the circle with radius L.As

a consequence we can treat A

in the most general case as x-independent.

However, the possibilities provided by gauge invariance are not exhausted

yet. There exist another class of legal gauge transformations which are not

periodic in x:

α(t, x) =

2π

nx n =±1, ±2,... . (4.167)

Since ∂α/∂x = const. and ∂α/∂t = 0 the periodicitiy of the gauge ﬁeld is not vio-

lated. For the phase factor exp(iα) the analogous assertion is valid- the difference

of phases at the endpoints of the interval [−L/2, L/2] is equal to 2πn.

As a result, we arrive at the conclusion that A

should not be considered in the

whole interval (−∞, +∞). The points A

, A

±2π/L, A

=±4π/L,etc.are

equivalent with respect to the gauge transformations (4.167) and must be iden-

tiﬁed. In other words, the variable A

should be considered only in the interval

[0, 2π/L]. Beyond this interval we ﬁnd gauge copies of this interval. In the com-

monly accepted terminology we may say that A

lives on the circle with length

2π/L.

222 4. Gauge Theories and Quantum-Chromodynamics

So far we considered the µ = 1 component of the gauge ﬁeld and this is

sufﬁcient if we consider the gauge ﬁeld as “external”. The µ = 0 component

of the gauge ﬁeld is then responsible for the Coulomb interaction between the

fermions. Since in two dimensions the Coulomb interaction grows linearly with

the distance between two fermions (conﬁnement) the corresponding effect is of

the order e

L at maximum. Now, if L is small, e

L  1, the Coulomb interaction

never becomes strong and we can neglect it in ﬁrst approximation.

Let us turn to global symmetries of the model. The Lagrange density with ﬁ-

nite L is invariant under multiplication of the fermion ﬁeld by a constant phase.

According to the famous theorem of E. Noether one easily derives from this

a conserved current which turns out to be identical with the usual electromag-

netic current:

Ψγ

Ψ,

Q(t) = 0 , Q(t) =

dxj

(t, x). (4.168)

The Lagrange density (4.158) admits another global symmetrie:

Ψ −→ e

iαγ

Ψ, (4.169)

which is called the global axial transformation. Again the theorem by Noether

ensures the existence of a conserved current J

5 µ

, the so called axial current,

which is conserved at the classical level just in the same way as the electro-

magnetic current. Note that the axial transformation multiplies the left- and

right-handed fermions by opposite phases. If the axial charge of the left-handed

fermion is Q

=+1, for the right-handed fermion Q

=−1.

The conservation of Q and Q

is equivalent to the conservation of the number

of the left-handed and right-handed fermions seperately. As we will see, in the

quantized theory only the sum of chiral charges is conserved, so only one out of

the two global symmetries of the classical theory survives the quantization of the

theory.

4.5.2 Dirac Sea

Let us now give a heuristic derivation of the chiral anomaly in the Schwinger

model on the circle before deducing it in a more rigorous manner.

In the two-dimensional electrodynamics the Dirac equation determining the

energy levels of the massless fermions is given by



∂

∂t

+σ



∂

∂x

− A



Ψ =0 . (4.170)

For the kth stationary state Ψ ∼exp(−iE

t)Ψ

(x) and the energy of the kth state

(x) =−σ



∂

∂x

− A



(x). (4.171)

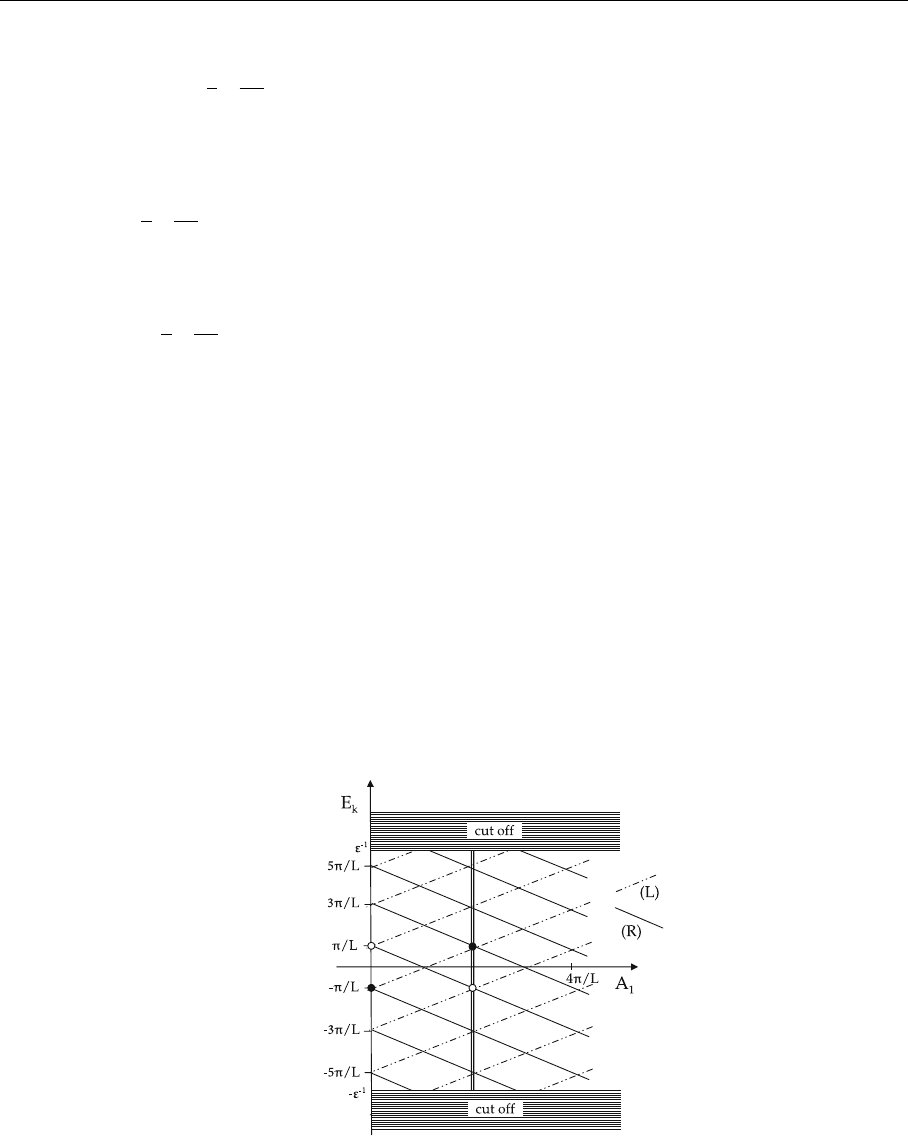
4.5 Extended Example: Anomalies in Gauge Theories 223

Furthermore, the eigenfunctions are proportional to

(x) ∼ exp





k +



2π



, k = 0, ±1, ±2,... . (4.172)

As a result, we conclude that the energy of the k th level for the left-handed

fermions is



k +



2π

+ A

, (4.173a)

while for the right-handed fermions

=−



k +



2π

− A

. (4.173b)

At A

=0, the energy levels for the left- and right-handed fermions are degener-

ate. If A

increases, the degeneracy is lifted and the levels are split. At the point

= 2π/L the structure of the energy levels is precisely the same as for A

= 0

– the degeneracy takes place again. This is the remnant of the gauge invariance

of the original theory. It is important to note that the identity of the points A

= 0

and A

= 2π/L is achieved in a non-trivial way. Since in passing from A

= 0to

= 2π/L a restructuring of the fermion levels take place. All left-handed lev-

els are shifted upwards by one interval, while all right-handed levels are shifted

downwards by the same one interval, as shown in Fig. 4.31. This phenomenon

lies on the basis of the chiral anomaly in the model at hand, as will become clear

shortly.

Let us now proceed to ﬁeld theory. The ﬁrst task is the construction of the

ground state. To this end, following the well-known Dirac-prescription we ﬁll

up all levels lying in the Dirac sea, leaving all positive-energy levels empty.

We will use



L,R

, k



for the ﬁlled and



L,R

, k



for the empty energy levels

Fig. 4.31. Energy levels for

right- and left-handed parti-

cles as function of the ﬁeld

. The open circles shows

the right-handed hole being

shifted down to negative en-

ergies, the full circle shows

the opposite behavior of a

ﬁlled negative energy left-

handed state moved to posi-

tive energies with increasing

ﬁeld

224 4. Gauge Theories and Quantum-Chromodynamics

with a given k . The subscript L (R ) indicates that we deal with left-handed

(right-handed) fermions.

At ﬁrst, the value of A

is ﬁxed in the vicintiy of zero. Then, the fermion

ground state, as seen from the ﬁgure, reduces to

| Ψ

ferm. vac.



⎛

⎝

k=−1,−2,...



, k

⎞

⎠

⊗

⎛

⎝

k=1,2,...



, k

⎞

⎠

⊗

⎛

⎝

k=0,1,2,...



, k

⎞

⎠

⊗

⎛

⎝

k=−1,−2,...



, k

⎞

⎠

.(4.174)

The Dirac sea, or all negative-energy levels are completely ﬁlled. Now let A

increase (adiabatically) from 0 to 2π/L.AtA

=2π/L the fermion ground state

(4.174) describes that state which, from the point of view of the normally ﬁlled

Dirac sea, contains one left-handed particle and one right-handed hole.

The interesting question is whether the quantum numbers of the fermions

change in the transition process from A

= 0toA

= 2π/L.Naivelywewould

say that the appearance of the particle and the hole does not change the electric

charge. In other words, the electromagnetic current is conserved. On the other

hand, the axial charges of the left handed particle and the right-handed hole are

the same (Q

=1) and, hence, in the transition at hand

∆Q

= 2 . (4.175)

Equation (4.175) can be rewritten as ∆Q

=(L/π) ∆ A

. Dividing by the

transition time we get

, (4.176)

which implies, in turn, that the conserved charge is given by



−



. (4.177)

The conserved current corresponding to this charge is

5 µ

= J

5 µ

−

µν

,∂·

= 0 ,∂· J

µν

∂

, (4.178)

where "

=−"

=1. The third equality in (4.178) is the famous axial

anomaly in the Schwinger model. We succeeded in deriving it by “hand-waving”

arguments by inspecting the picture of motion of the fermion levels in the ex-

ternal ﬁeld A

(t). It turns out that in this language the axial (or chiral) anomaly

presents a widely known phenomenon: the crossing of the zero point in the en-

ergy scale by a group of levels. The presence of the inﬁnite number of levels and

the Dirac picture, according to which the emergence of a ﬁlled level from the

sea means the appearance of a particle while the submergence of an empty level

4.5 Extended Example: Anomalies in Gauge Theories 225

into the sea is equivalent to the production of a hole, are the most essential elem-

ents of the whole construction.

With a ﬁnite number of levels there can be no

anomaly.

4.5.3 Ultraviolet Regularization

In spite of the transparent character of this heuristic derivation almost all of

the “evident” arguments above can be questioned by the careful reader. Indeed,

why is the fermion ground state (4.174) the appropriate choice? In what sense is

the energy of this state minimal, taking into account the fact that, according to

(4.173a) and (4.173b)

E ∼−

∞



k=0



k +



2π

, (4.179)

and the series is divergent?

The ground state (4.174) describing the fermion sector at A

= 0 contains, in

particular, the direct product of an inﬁnite large number of ﬁlled states with nega-

tive energy. It is clear that the inﬁnite product is ill-deﬁned, and one cannot do

without regularization in calculating physical quantities. The contribution from

large momenta should be somehow cut off.

In order to preserve the gauge invariance, it is possible and convenient to use

the regularization called the Schwinger- or ε-splitting. The regularization will

provide a more solid basis to the heuristic derivation presented above. Instead of

the original currents

(t, x) =

Ψ(t, x)γ

Ψ(t, x), J

5 µ

(t, x) =

Ψ(t, x)γ

Ψ(t, x), (4.180)

we introduce the regularized objects

reg

(t, x) =

Ψ(t, x +ε) γ

Ψ(t, x) exp

⎛

⎝

−i

x+ε

dx A

⎞

⎠

reg

5 µ

(t, x) =

Ψ(t, x +ε) γ

Ψ(t, x) exp

⎛

⎝

−i

x+ε

dx A

⎞

⎠

. (4.181)

In the calculation of physical quantities the limit ε −→ 0 is always implied. At

the intermediate stages, however, all computations are performed with ﬁxed ε.

Note the similarity of this effect to the diving of an empty electron state into the lower

continuum in the presence of a supercritical external electric ﬁeld. The hole in the

lower continuum is subsequently emitted as a so-called spontaneous positron (for fur-

ther details of the supercritical change of the neutral vacuum into a charged vacuum

due to Coulomb ﬁelds by spontaneous positron emission, see W. Greiner, B. Müller, J.

Rafelski: Quantum Electrodynamics of Strong Fields, (Springer, Berlin, Heidelberg,

1985), pp 122.

226 4. Gauge Theories and Quantum-Chromodynamics

The exponential factor in (4.181) ensures gauge invariance of the non-local

(“split”) currents. Without this exponential any composite operator like the

electromagnetic current or the axial current transforms under the local phase

transformations (4.165) like

†

(t, x +ε) Ψ

(t, x)

−→ exp

[

−iα(x +ε) +iα(x)

]

†

(t, x +ε) Ψ

(t, x). (4.182)

The gauge transformation of A

−→ A

−∂α(x)/∂x) compensates for the

phase factor in (4.182).

Now, there is no difﬁculty to calculate the electric and axial charges of the

state (4.174). If

Q(t) =

dxJ

reg

(t, x), Q

(t) =

dxJ

reg

(t, x), (4.183)

then we get for the fermion ground state

Q = Q

, Q

= Q

−Q

, (4.184)

−∞



k=−1

exp

(

−iε E

)

−∞



k=−1

exp

−iε



k +



2π

+ A

&

, (4.185)

+∞



k=0

exp

(

+iε E

)

+∞



k=0

exp

−iε



k +



2π

+ A

&

. (4.186)

In the limit ε −→ 0 both charges, Q

and Q

, turn into the sum of units – each

unit represents one ﬁlled level from the Dirac sea. Performing the summation

−iε A

1 −e

+iε 2π/L

, (4.187)

−iε A

1 −e

−iε 2π/L

(4.188)

and expanding in ε we arrive at

−iε2π

2π

+O(ε) , (4.189)

+iε2π

−

2π

+O(ε) (4.190)

for the fermion ground state (4.174).

4.5 Extended Example: Anomalies in Gauge Theories 227

Equations (4.189) show that under our choice of the fermion ground state

the charge of the vacuum vanishes, Q = Q

=0. There is no time depen-

dence – the charge is conserved. The axial charge consists of two terms: the ﬁrst

represents an inﬁnitely large constant and the second one gives a linear A

de-

pendence. In the transition from A

= 0toA

= 2π/L the axial charge changes

by two units.

These conclusions are not new for us. We have found just the same from the

illustrative picture described above in which the electric and axial charges of the

Dirac sea are determined intuitively. Now we learned how to sum up the inﬁnite

series of units, i.e. the charges of the “left-handed” and “right-handed” seas.

It is very important to note, that there is no regularization ensuring simulta-

neously the gauge invariance and conservation of the axial current.

Now, we leave the issue of charges and proceed to the calculation of the

fermion-sea energy, the problem which could not be solved at the naive level,

without regularization. Fortunately, all necessary elements are already prepared.

The fermion part of the Hamiltonian

H =−Ψ

†

(t, x)σ



∂

∂x

− A



Ψ(t, x) (4.191)

reduces after the ε-splitting to

reg

=−Ψ

†

(t, x +ε) σ



∂

∂x

− A



Ψ(t, x) exp

⎛

⎝

−i

x+ε

dx A

⎞

⎠

(4.192)

This formula implies the following regularized expressions for the energy of the

“left-handed” and “right-handed” seas:

−∞



k=−1

exp

(

−iε E

)

, (4.193a)

+∞



k=0

exp

(

+iε E

)

, (4.193b)

where the energies of the individual levels E

kL,R

are given in (4.173a) and

(4.173b) and the summation runs over all levels with negative energy. The ex-

pressions (4.193a) and (4.193b) have the following meaning: in the limit ε −→ 0

they reduce to the sum of the energies of all ﬁlled fermion levels from the Dirac

sea. Notice, that E

and E

can be obtained by differentiating the expressions

(4.185) and (4.186) for Q

L,R

with respect to ε:

=+i

∂

∂ε

=+i

∂

∂ε

−iε A

1 −e

+iε 2π/L

, (4.194a)

=−i

∂

∂ε

=−i

∂

∂ε

−iε A

1 −e

−iε 2π/L

, (4.194b)